角点检测：Harris 与 Shi-Tomasi原理拆解【计算机视觉】

[角点检测（Corner Detection）](#角点检测（Corner Detection）)
- Ⅰ、引言
- [Ⅱ、Harris 角点检测](#Ⅱ、Harris 角点检测)
- - [一、Harris 角点检测的本质](#一、Harris 角点检测的本质)
  - [二、Harris 角点检测算法数学原理](#二、Harris 角点检测算法数学原理)
  - - [1. 定义窗口移动的灰度变化函数](#1. 定义窗口移动的灰度变化函数)
    - [2. 数学简化：一阶泰勒展开与二次型转化](#2. 数学简化：一阶泰勒展开与二次型转化)
    - [3. 结构矩阵： M M M的性质与意义](#3. 结构矩阵： M M M的性质与意义)
    - [4. 判断依据：Harris 响应值 R R R 构造](#4. 判断依据：Harris 响应值 R R R 构造)
    - [5. 核心判断：由 R R R 区分区域类型](#5. 核心判断：由 R R R 区分区域类型)
    - [6. 数学流程](#6. 数学流程)
- [Ⅲ、Shi-Tomasi 角点检测](#Ⅲ、Shi-Tomasi 角点检测)
- - [一、Shi-Tomasi是对 Harris 角点理论的简化与改进](#一、Shi-Tomasi是对 Harris 角点理论的简化与改进)
  - 二、Shi-Tomasi的数学原理
  - - 1.核心思想
    - [2. 数学定义](#2. 数学定义)
    - [3. 区域分类直观解释](#3. 区域分类直观解释)
    - [4. 与 Harris 角点的对比总结](#4. 与 Harris 角点的对比总结)
    - [5. 工程实现说明](#5. 工程实现说明)
- Ⅳ、代码对比不同角点检测的结果
- - 一、代码实现
  - 二、结果分析
  - - [1. 红点多绿点少的原因](#1. 红点多绿点少的原因)
    - [2. 具体细节拆解](#2. 具体细节拆解)
    - [3. 总结](#3. 总结)
- Ⅴ、角点检测算法在图像拼接的应用
- Ⅵ、总结

角点检测（Corner Detection）

角点是图像中各方向灰度变化显著的关键特征点，角点检测即通过算法自动提取这类可支撑后续视觉任务的核心锚点。

注意：本文所有代码均可导入 Jupyter Notebook 直接运行

Ⅰ、引言

在计算机视觉的世界里，我们常常需要让机器像人类一样 "看懂" 图像内容 ------ 而要实现这一点，第一步往往不是直接识别完整的物体，而是先抓住图像中那些 "关键的锚点"。

想象一下，当你观察一张桌子的照片时，你的目光会不自觉地先落在桌子的四个拐角；当你看一幅建筑蓝图时，墙体的交接处、窗户的边角会最先吸引你的注意力。这些在图像中具有明显特征、能够代表局部结构信息的点，就是我们今天要探讨的核心 ------ 角点（Corner）。

角点的独特之处在于，它在各个方向上的灰度变化都非常显著，既不像平坦区域那样灰度趋于一致，也不像边缘那样只在单一方向上有明显变化。而角点检测（Corner Detection），就是通过算法自动从图像中提取这些关键锚点的过程。

Ⅱ、Harris 角点检测

一、Harris 角点检测的本质

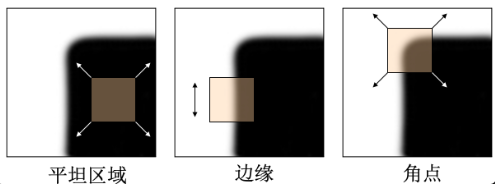
通过计算图像中某个像素点周围区域，在不同方向上移动后的灰度变化程度，来判断该点是否为角点。

若某个点向任意方向移动，灰度都发生剧烈变化 → 这是角点
若某个点只在一个方向上移动有灰度变化，其他方向无 → 这是边缘
若某个点向任意方向移动，灰度都几乎无变化 → 这是平坦区域

二、Harris 角点检测算法数学原理

以下公式涵盖 Harris 角点检测的全流程，从图像预处理到最终角点提取，所有核心数学推导与计算步骤均完整呈现。

输入：彩色/灰度图像 (I(x,y))
输出：图像中的有效角点集合
核心参数：高斯窗口大小、经验常数 (k)、响应值阈值 (T)

1. 定义窗口移动的灰度变化函数

以任意像素为中心取邻域窗口 W W W，定义窗口沿 ( Δ x , Δ y ) (\Delta x, \Delta y) (Δx,Δy) 移动后，窗口内的总灰度变化量为：
E ( Δ x , Δ y ) = ∑ ( u , v ) ∈ W w ( u , v ) ⋅ [ I ( u + Δ x , v + Δ y ) − I ( u , v ) ] 2 E(\Delta x, \Delta y) = \sum_{(u,v) \in W} w(u,v) \cdot [I(u+\Delta x, v+\Delta y) - I(u,v)]^2 E(Δx,Δy)=(u,v)∈W∑w(u,v)⋅[I(u+Δx,v+Δy)−I(u,v)]2
核心符号说明

E ( Δ x , Δ y ) E(\Delta x, \Delta y) E(Δx,Δy)：窗口移动后的总灰度变化值
w ( u , v ) w(u,v) w(u,v)：高斯加权函数（赋予窗口中心像素更高权重，提升原理的鲁棒性）
I ( u , v ) I(u,v) I(u,v)：像素 ( u , v ) (u,v) (u,v) 的灰度值
W W W：像素邻域窗口（原理层面不限制大小）

高斯加权函数 w ( u , v ) w(u,v) w(u,v) 完整定义
w ( u , v ) w(u,v) w(u,v) 是以当前像素 ( x , y ) (x,y) (x,y) 为中心的二维高斯加权函数 ，用于对邻域梯度进行平滑加权，提升角点检测的抗噪性与稳定性，其数学表达式为：
w ( u , v ) = 1 2 π σ 2 exp ⁡ ( − ( u − x ) 2 + ( v − y ) 2 2 σ 2 ) w(u,v) = \frac{1}{2\pi\sigma^2} \exp\left(-\frac{(u-x)^2 + (v-y)^2}{2\sigma^2}\right) w(u,v)=2πσ21exp(−2σ2(u−x)2+(v−y)2)

其中：

( x , y ) (x,y) (x,y) 为当前计算Harris响应的中心像素

( u , v ) (u,v) (u,v) 为局部窗口内任意像素

σ \sigma σ 为高斯核标准差，控制加权衰减速度

距离中心越近， w ( u , v ) w(u,v) w(u,v) 越大；距离越远， w ( u , v ) w(u,v) w(u,v) 越小
该权重会代入结构矩阵完成邻域梯度的加权求和：
M = ∑ ( u , v ) ∈ W w ( u , v ) [ I x 2 I x I y I x I y I y 2 ] M = \sum_{(u,v)\in W} w(u,v) \begin{bmatrix} I_x^2 & I_xI_y \\ I_xI_y & I_y^2 \end{bmatrix} M=(u,v)∈W∑w(u,v)[Ix2IxIyIxIyIy2]

2. 数学简化：一阶泰勒展开与二次型转化

直接计算上述函数复杂度较高，通过二元函数一阶泰勒展开 忽略高阶无穷小，在点 ( u , v ) (u,v) (u,v) 处对灰度函数做近似：
I ( u + Δ x , v + Δ y ) ≈ I ( u , v ) + I x ( u , v ) Δ x + I y ( u , v ) Δ y I(u+\Delta x, v+\Delta y) \approx I(u,v) + I_x(u,v)\Delta x + I_y(u,v)\Delta y I(u+Δx,v+Δy)≈I(u,v)+Ix(u,v)Δx+Iy(u,v)Δy

其中， I x ( u , v ) = ∂ I ∂ x ( u , v ) I_x(u,v) = \frac{\partial I}{\partial x}(u,v) Ix(u,v)=∂x∂I(u,v)、 I y ( u , v ) = ∂ I ∂ y ( u , v ) I_y(u,v) = \frac{\partial I}{\partial y}(u,v) Iy(u,v)=∂y∂I(u,v) 为图像在像素 ( u , v ) (u,v) (u,v) 处的水平、垂直灰度梯度，描述该点灰度沿对应方向的变化率。

此处使用一阶泰勒展开的核心原因：

图像灰度函数 I ( u , v ) I(u,v) I(u,v)是离散像素构成的非线性函数，无显式解析表达式，无法直接对其进行极值分析、矩阵化推导（后续二次型、结构矩阵 M M M的构建）。

而角点检测仅关注窗口局部微小偏移 ( Δ x , Δ y ) (\Delta x,\Delta y) (Δx,Δy)，在微小增量前提下，泰勒展开可将非线性的灰度偏移项 I ( u + Δ x , v + Δ y ) I(u+\Delta x,v+\Delta y) I(u+Δx,v+Δy)，近似为仅含当前点灰度和可计算梯度 I x 、 I y I_x、I_y Ix、Iy的线性式，既简化计算，又能衔接后续二次型、特征值的理论分析，是Harris角点检测数学建模的关键近似步骤。

将上式代入灰度变化函数，先得到灰度差：
I ( u + Δ x , v + Δ y ) − I ( u , v ) ≈ I x ( u , v ) Δ x + I y ( u , v ) Δ y I(u+\Delta x,v+\Delta y)-I(u,v) \,\approx\, I_x(u,v)\Delta x + I_y(u,v)\Delta y I(u+Δx,v+Δy)−I(u,v)≈Ix(u,v)Δx+Iy(u,v)Δy

代入 E ( Δ x , Δ y ) E(\Delta x,\Delta y) E(Δx,Δy) 的定义：
E ( Δ x , Δ y ) ≈ ∑ ( u , v ) ∈ W w ( u , v ) ⋅ [ I x ( u , v ) Δ x + I y ( u , v ) Δ y ] 2 E(\Delta x, \Delta y) \,\approx\, \sum_{(u,v)\in W} w(u,v) \cdot\big[I_x(u,v)\Delta x + I_y(u,v)\Delta y\big]^2 E(Δx,Δy)≈(u,v)∈W∑w(u,v)⋅[Ix(u,v)Δx+Iy(u,v)Δy]2

将平方项完全展开：
( I x ( u , v ) Δ x + I y ( u , v ) Δ y ) 2 = I x ( u , v ) 2 Δ x 2 + 2 I x ( u , v ) I y ( u , v ) Δ x Δ y + I y ( u , v ) 2 Δ y 2 \big(I_x(u,v)\Delta x + I_y(u,v)\Delta y\big)^2 = I_x(u,v)^2\Delta x^2 + 2I_x(u,v)I_y(u,v)\Delta x\Delta y + I_y(u,v)^2\Delta y^2 (Ix(u,v)Δx+Iy(u,v)Δy)2=Ix(u,v)2Δx2+2Ix(u,v)Iy(u,v)ΔxΔy+Iy(u,v)2Δy2

由于 Δ x , Δ y \Delta x,\Delta y Δx,Δy 是窗口整体偏移量，与窗口内像素位置 ( u , v ) (u,v) (u,v) 无关，可将其提出求和符号，并定义窗口内加权梯度累加量：
A = ∑ ( u , v ) ∈ W w ( u , v ) I x ( u , v ) 2 , B = ∑ ( u , v ) ∈ W w ( u , v ) I y ( u , v ) 2 , C = ∑ ( u , v ) ∈ W w ( u , v ) I x ( u , v ) I y ( u , v ) A = \sum_{(u,v)\in W} w(u,v)\,I_x(u,v)^2,\quad B = \sum_{(u,v)\in W} w(u,v)\,I_y(u,v)^2,\quad C = \sum_{(u,v)\in W} w(u,v)\,I_x(u,v)I_y(u,v) A=(u,v)∈W∑w(u,v)Ix(u,v)2,B=(u,v)∈W∑w(u,v)Iy(u,v)2,C=(u,v)∈W∑w(u,v)Ix(u,v)Iy(u,v)

此时 E E E 可表示为二次多项式：
E ( Δ x , Δ y ) ≈ A Δ x 2 + 2 C Δ x Δ y + B Δ y 2 E(\Delta x, \Delta y) \,\approx\, A\Delta x^2 + 2C\Delta x\Delta y + B\Delta y^2 E(Δx,Δy)≈AΔx2+2CΔxΔy+BΔy2

上式为标准二元二次型，可写成矩阵乘法形式，从而得到原理核心简化结果 ：

Δ x Δ y \] \[ A C C B \] \[ Δ x Δ y \] = A Δ x 2 + 2 C Δ x Δ y + B Δ y 2 \\begin{bmatrix} \\Delta x \& \\Delta y \\end{bmatrix} \\begin{bmatrix} A \& C \\\\ C \& B \\end{bmatrix} \\begin{bmatrix} \\Delta x \\\\ \\Delta y \\end{bmatrix} = A\\Delta x\^2 + 2C\\Delta x\\Delta y + B\\Delta y\^2 \[ΔxΔy\]\[ACCB\]\[ΔxΔy\]=AΔx2+2CΔxΔy+BΔy2 E ( Δ x , Δ y ) ≈ \[ Δ x Δ y \] ⋅ M ⋅ \[ Δ x Δ y \] E(\\Delta x, \\Delta y) \\approx \\begin{bmatrix} \\Delta x \& \\Delta y \\end{bmatrix} \\cdot M \\cdot \\begin{bmatrix} \\Delta x \\\\ \\Delta y \\end{bmatrix} E(Δx,Δy)≈\[ΔxΔy\]⋅M⋅\[ΔxΔy

其中 Harris 结构矩阵为：

M = [ A C C B ] = ∑ ( u , v ) ∈ W w ( u , v ) [ I x ( u , v ) 2 I x ( u , v ) I y ( u , v ) I x ( u , v ) I y ( u , v ) I y ( u , v ) 2 ] M=\begin{bmatrix}A&C\\C&B\end{bmatrix} =\sum_{(u,v)\in W}w(u,v) \begin{bmatrix} I_x(u,v)^2&I_x(u,v)I_y(u,v)\\ I_x(u,v)I_y(u,v)&I_y(u,v)^2 \end{bmatrix} M=[ACCB]=(u,v)∈W∑w(u,v)[Ix(u,v)2Ix(u,v)Iy(u,v)Ix(u,v)Iy(u,v)Iy(u,v)2]

3. 结构矩阵： M M M的性质与意义

多项式只能算出单个偏移下的变化数值，矩阵才能揭示变化的几何结构，而角点判定依赖的正是这种结构，而非单个数值。

在上文二次型化简中，我们已经得到 Harris 结构矩阵：
M = ∑ ( u , v ) ∈ W w ( u , v ) [ I x ( u , v ) 2 I x ( u , v ) I y ( u , v ) I x ( u , v ) I y ( u , v ) I y ( u , v ) 2 ] = [ A C C B ] M = \sum_{(u,v) \in W} w(u,v) \begin{bmatrix} I_x(u,v)^2 & I_x(u,v)I_y(u,v) \\ I_x(u,v)I_y(u,v) & I_y(u,v)^2 \end{bmatrix} = \begin{bmatrix} A & C \\ C & B \end{bmatrix} M=(u,v)∈W∑w(u,v)[Ix(u,v)2Ix(u,v)Iy(u,v)Ix(u,v)Iy(u,v)Iy(u,v)2]=[ACCB]

其中 (A,B,C) 为窗口内梯度的加权累加量。

M M M 的核心性质：

M M M是 ( 2 × 2 ) (2 \times 2) (2×2) 对称半正定矩阵，特征值 ( λ 1 , λ 2 ) (\lambda_1,\lambda_2) (λ1,λ2) 均为非负实数
M M M用于描述当前像素邻域内的灰度梯度分布，特征值大小对应不同方向上的灰度变化强度

4. 判断依据：Harris 响应值 R R R 构造

在前面的推导中，我们已经将灰度变化能量函数 E ( Δ x , Δ y ) E(\Delta x,\Delta y) E(Δx,Δy)转化为关于位移向量的二次型，其局部变化特性完全由结构矩阵 M M M的两个特征值 λ 1 , λ 2 \lambda_1,\lambda_2 λ1,λ2决定。理论上可以通过逐点计算特征值并判断大小，区分平坦区域、边缘与角点，但直接对每个像素位置求解 2 × 2 2\times2 2×2矩阵的特征值，会带来额外的开方、特征分解运算，在图像逐像素遍历场景下计算开销偏大。

因此在工程与理论实现中，不直接显式求解 λ 1 , λ 2 \lambda_1,\lambda_2 λ1,λ2，而是利用对称矩阵的基本代数性质，使用矩阵的行列式 与迹这两个可快速计算的标量量，构造统一的角点响应函数 R R R，实现对像素类型的快速判别。

矩阵关键统计量与特征值的关系

结构矩阵 M = [ A C C B ] M=\begin{bmatrix}A&C\\C&B\end{bmatrix} M=[ACCB]是实对称半正定矩阵，拥有两个非负实数特征值 λ 1 , λ 2 \lambda_1,\lambda_2 λ1,λ2，满足对称矩阵的核心恒等关系：

行列式 ：矩阵所有特征值的乘积，计算公式与特征值关系为
det ⁡ ( M ) = A B − C 2 = λ 1 λ 2 \det(M) = AB - C^2 = \lambda_1 \lambda_2 det(M)=AB−C2=λ1λ2
物理含义：用于量化两个特征值的整体乘积大小，反映灰度变化在两个正交主方向上的联合强度。
迹：矩阵主对角线元素之和，等于所有特征值的和，计算公式与特征值关系为
tr ( M ) = A + B = λ 1 + λ 2 \text{tr}(M) = A + B = \lambda_1 + \lambda_2 tr(M)=A+B=λ1+λ2
物理含义：用于量化两个特征值的整体总和大小，反映灰度变化在两个主方向上的总强度。

利用这两个恒等式，无需执行特征分解，仅通过矩阵元素的四则运算即可完成与特征值强相关的数值计算。

Harris 响应值公式与设计思想

结合行列式与迹，定义Harris角点响应值 R R R：
R = det ⁡ ( M ) − k ⋅ [ tr ( M ) ] 2 R = \det(M) - k \cdot \left[\text{tr}(M)\right]^2 R=det(M)−k⋅[tr(M)]2

代入特征值表达，可得到等价形式：
R = λ 1 λ 2 − k ( λ 1 + λ 2 ) 2 R = \lambda_1\lambda_2 - k(\lambda_1+\lambda_2)^2 R=λ1λ2−k(λ1+λ2)2

各组成部分与参数的详细含义：

det ⁡ ( M ) = λ 1 λ 2 \det(M)=\lambda_1\lambda_2 det(M)=λ1λ2：当两个方向灰度变化都显著时，该项取值较大；若存在一个方向变化极小（边缘），该项会快速减小；平坦区域则趋近于0。
tr ( M ) = λ 1 + λ 2 \text{tr}(M)=\lambda_1+\lambda_2 tr(M)=λ1+λ2：对单一方向大变化（边缘）和两个方向都大变化（角点）都会有较大响应，需要通过系数与平方项进行抑制。
k k k：经验调节常数，由实验确定，通用取值范围为 0.04 ∼ 0.06 0.04 \sim 0.06 0.04∼0.06 ，作用是平衡行列式与迹的贡献，避免边缘区域被误判为角点。 k k k过大会降低角点灵敏度， k k k过小则边缘抑制效果变差。
R R R：逐像素计算得到的标量响应值，用于统一量化该像素位置为角点的置信程度，是后续阈值筛选的直接依据。

5. 核心判断：由 R R R 区分区域类型

基于响应值 R R R的区域分类规则

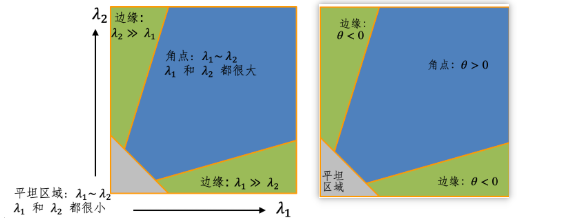
结合 λ 1 , λ 2 \lambda_1,\lambda_2 λ1,λ2的物理意义与 R R R的表达式，可以直接通过 R R R的符号与幅值完成三类区域的判别：

角点
λ 1 \lambda_1 λ1与 λ 2 \lambda_2 λ2均较大且数值接近，使得 λ 1 λ 2 \lambda_1\lambda_2 λ1λ2远大于 k ( λ 1 + λ 2 ) 2 k(\lambda_1+\lambda_2)^2 k(λ1+λ2)2，满足：
R ≫ 0 R \gg 0 R≫0

代表两个正交方向灰度均发生剧烈变化，符合角点定义。
边缘

一个特征值很大，另一个特征值近似为0 ，代入后 λ 1 λ 2 \lambda_1\lambda_2 λ1λ2项很小，整体满足：
R ≪ 0 R \ll 0 R≪0

代表仅单一方向存在明显灰度变化，对应图像边缘。
平坦区域
λ 1 \lambda_1 λ1与 λ 2 \lambda_2 λ2均接近于0 ，两项都很小，最终：
R ≈ 0 R \approx 0 R≈0

代表任意方向灰度变化均极微弱，为纹理平坦区域。

6. 数学流程

E ( Δ x , Δ y ) → 泰勒展开二次型 → M → R → 阈值判断角点 E(\Delta x,\Delta y) \xrightarrow{\text{泰勒展开}} \text{二次型} \xrightarrow{} M \xrightarrow{} R \xrightarrow{\text{阈值判断}} \text{角点} E(Δx,Δy)泰勒展开二次型 M R阈值判断角点

Ⅲ、Shi-Tomasi 角点检测

一、Shi-Tomasi是对 Harris 角点理论的简化与改进

Harris 角点通过构造响应值 R = det ⁡ ( M ) − k ⋅ t r ( M ) 2 R=\det(M)-k\cdot\mathrm{tr}(M)^2 R=det(M)−k⋅tr(M)2 实现角点判定，但存在一个明显不足： R R R 对经验参数 k k k 敏感，不同图像、不同纹理需要微调 k k k 才能获得稳定结果；且 R R R 是 λ 1 , λ 2 \lambda_1,\lambda_2 λ1,λ2 的组合式，物理直观性较弱。

Shi-Tomasi 方法直接从二次型极值的物理意义 出发，跳过人工构造 R R R 的环节，使用更直接、更稳定的判定准则，是对 Harris 角点理论的简化与改进，也是视觉跟踪、稀疏重建中更常用的角点提取方式。

二、Shi-Tomasi的数学原理

1.核心思想

在之前推导中已经得到：

在单位位移向量约束 Δ x 2 + Δ y 2 ≈ 1 \Delta x^2+\Delta y^2\approx 1 Δx2+Δy2≈1 下，二次型能量函数

E ( Δ x , Δ y ) = [ Δ x Δ y ] M [ Δ x Δ y ] E(\Delta x,\Delta y) = \begin{bmatrix}\Delta x & \Delta y\end{bmatrix} M \begin{bmatrix}\Delta x \\ \Delta y\end{bmatrix} E(Δx,Δy)=[ΔxΔy]M[ΔxΔy]

的极值由结构矩阵 M M M 的特征值 λ 1 , λ 2 \lambda_1,\lambda_2 λ1,λ2 直接决定：

min ⁡ ∣ ∣ ( Δ x , Δ y ) ∣ ∣ = 1 E = min ⁡ ( λ 1 , λ 2 ) , max ⁡ ∣ ∣ ( Δ x , Δ y ) ∣ ∣ = 1 E = max ⁡ ( λ 1 , λ 2 ) \min_{||(\Delta x,\Delta y)||=1} E = \min(\lambda_1,\lambda_2),\quad \max_{||(\Delta x,\Delta y)||=1} E = \max(\lambda_1,\lambda_2) ∣∣(Δx,Δy)∣∣=1minE=min(λ1,λ2),∣∣(Δx,Δy)∣∣=1maxE=max(λ1,λ2)

角点的本质要求是：所有方向上灰度变化都足够大 ，即变化最小的那个方向，变化量也不能小。

因此最直观的判定条件是：
min ⁡ ( λ 1 , λ 2 ) > T \min(\lambda_1,\lambda_2) > T min(λ1,λ2)>T

其中 T T T 为人工设定的响应阈值。这就是 Shi-Tomasi 的核心判据。

2. 数学定义

设结构矩阵 M M M 的两个非负实特征值满足 λ 1 ≥ λ 2 ≥ 0 \lambda_1\ge\lambda_2\ge 0 λ1≥λ2≥0，定义 Shi-Tomasi 角点响应为较小特征值本身：
R Shi-Tomasi = min ⁡ ( λ 1 , λ 2 ) R_{\text{Shi-Tomasi}} = \min(\lambda_1,\lambda_2) RShi-Tomasi=min(λ1,λ2)

判定规则：

若 R Shi-Tomasi > T R_{\text{Shi-Tomasi}} > T RShi-Tomasi>T：判定为角点
若 R Shi-Tomasi ≤ T R_{\text{Shi-Tomasi}} \le T RShi-Tomasi≤T：判定为非角点（边缘或平坦区域）

与 Harris 对比：

Harris：依赖人工设计 R = λ 1 λ 2 − k ( λ 1 + λ 2 ) 2 R=\lambda_1\lambda_2 - k(\lambda_1+\lambda_2)^2 R=λ1λ2−k(λ1+λ2)2，引入超参 k k k
Shi-Tomasi：直接使用 min ⁡ ( λ 1 , λ 2 ) \min(\lambda_1,\lambda_2) min(λ1,λ2)，无额外经验系数，物理意义清晰

3. 区域分类直观解释

对图像不同区域，特征值满足不同关系，对应 Shi-Tomasi 响应不同：

平坦区域
λ 1 ≈ 0 , λ 2 ≈ 0 ⟹ min ⁡ ( λ 1 , λ 2 ) ≈ 0 \lambda_1\approx 0,\;\lambda_2\approx 0 \implies \min(\lambda_1,\lambda_2)\approx 0 λ1≈0,λ2≈0⟹min(λ1,λ2)≈0，不满足阈值，被剔除。
边缘区域

一个特征值大，一个特征值接近 0，例如 λ 1 ≫ 0 , λ 2 ≈ 0 \lambda_1 \gg 0,\;\lambda_2\approx 0 λ1≫0,λ2≈0
⟹ min ⁡ ( λ 1 , λ 2 ) ≈ 0 \implies \min(\lambda_1,\lambda_2)\approx 0 ⟹min(λ1,λ2)≈0，不满足阈值，被剔除。
角点区域
λ 1 , λ 2 \lambda_1,\lambda_2 λ1,λ2 均显著大于 0
⟹ min ⁡ ( λ 1 , λ 2 ) > T \implies \min(\lambda_1,\lambda_2) > T ⟹min(λ1,λ2)>T，被保留为角点。

可以看到：Shi-Tomasi 天然具备区分边缘与角点 的能力，且不需要额外系数 k k k。

4. 与 Harris 角点的对比总结

对比项	Harris 角点	Shi-Tomasi（Good Features to Track）
响应函数	R = det ⁡ ( M ) − k ⋅ t r ( M ) 2 R=\det(M)-k\cdot\mathrm{tr}(M)^2 R=det(M)−k⋅tr(M)2	R = min ⁡ ( λ 1 , λ 2 ) R=\min(\lambda_1,\lambda_2) R=min(λ1,λ2)
经验参数	有 k k k，通常取 0.04 ∼ 0.06 0.04\sim 0.06 0.04∼0.06	无额外经验参数，仅保留阈值 T T T
物理直观性	间接，由特征值组合构造	直接对应最小变化方向的能量大小，意义明确
稳定性	对 k k k 敏感，不同图像需要调参	对纹理、图像变化更稳定
典型用途	通用角点检测	光流跟踪、稀疏SLAM、特征匹配、KLT跟踪中首选

5. 工程实现说明

虽然形式上需要计算特征值，但 2 × 2 2\times2 2×2 实对称矩阵的特征值存在闭式解：
λ 1 , 2 = t r ( M ) 2 ± ( t r ( M ) 2 ) 2 − det ⁡ ( M ) \lambda_{1,2} = \frac{\mathrm{tr}(M)}{2} \pm \sqrt{\left(\frac{\mathrm{tr}(M)}{2}\right)^2 - \det(M)} λ1,2=2tr(M)±(2tr(M))2−det(M)

仍然可以只用 A , B , C A,B,C A,B,C（即 t r ( M ) = A + B , det ⁡ ( M ) = A B − C 2 \mathrm{tr}(M)=A+B,\;\det(M)=AB-C^2 tr(M)=A+B,det(M)=AB−C2）快速算出两个特征值，再取较小者，不需要迭代算法，计算开销与 Harris 接近。

Ⅳ、代码对比不同角点检测的结果

一、代码实现

python 复制代码

import cv2
import numpy as np
import matplotlib.pyplot as plt

def get_test_image():
    img = cv2.imread("test2.jpg")

    # 读取失败时，生成备用人工棋盘格图（防止程序报错）
    if img is None:
        print("提示：未找到，自动生成备用人工角点图")
        img = np.ones((400, 400, 3), dtype=np.uint8) * 255
        grid_step = 80
        for i in range(0, 401, grid_step):
            cv2.line(img, (i, 0), (i, 400), (0, 0, 0), 2)
            cv2.line(img, (0, i), (400, i), (0, 0, 0), 2)

    return img

# 获取统一测试图像
test_img = get_test_image()
# 转为灰度图（两种算法均需要灰度输入）
test_gray = cv2.cvtColor(test_img, cv2.COLOR_BGR2GRAY)

这段代码定义了一个名为harris_corner_detect的封装函数，核心作用是调用 OpenCV 的 Harris 角点检测接口，完成从输入图像到标记红色角点结果图的全流程，同时返回算法生成的角点响应图。它隐藏了 Harris 检测的底层细节，只暴露关键可调参数，方便用户直接调用，且输出格式统一，便于后续和其他角点检测算法做对比。

python 复制代码

def harris_corner_detect(img, gray, block_size=2, ksize=3, k=0.04, threshold=0.01):
    # 转换为 32 位浮点型（Harris 要求输入格式）
    gray_float = np.float32(gray)
    # 调用 Harris 角点检测
    harris_dst = cv2.cornerHarris(gray_float, blockSize=block_size, ksize=ksize, k=k)
    # 膨胀结果（增强角点显示效果，非必需）
    harris_dst = cv2.dilate(harris_dst, None)
    # 复制原始图像用于绘制角点
    img_harris = img.copy()
    # 标记角点（红色：BGR 格式 (0, 0, 255)）
    img_harris[harris_dst > threshold * harris_dst.max()] = (0, 0, 255)
    return img_harris, harris_dst

函数内部先将灰度图转换为 32 位浮点型，满足cv2.cornerHarris的输入格式要求，随后调用该接口得到全图像素的角点响应图harris_dst，再通过膨胀操作优化角点的显示效果。接着复制原始彩色图像，避免修改原图，通过阈值筛选出高置信度的角点区域，将这些区域的像素设为 BGR 格式的红色，完成角点可视化标记，最后返回标记好的彩色结果图和原始响应图，既满足直观查看需求，也保留了原始数据供后续分析。

这段代码定义了一个名为shi_tomasi_corner_detect的封装函数，核心作用是调用 OpenCV 官方的cv2.goodFeaturesToTrack接口实现纯 Shi-Tomasi 角点检测，输出标记了绿色实心圆角点的彩色图像，同时返回检测到的角点坐标，格式统一且易用，方便与 Harris 角点检测结果做对比。

python 复制代码

def shi_tomasi_corner_detect(img, gray, max_corners=150, quality_level=0.01, min_distance=10):
    # 调用 Shi-Tomasi 角点检测（OpenCV 官方接口：goodFeaturesToTrack）
    corners = cv2.goodFeaturesToTrack(
        gray,
        maxCorners=max_corners,       # 最大检测角点数量
        qualityLevel=quality_level,   # 角点质量阈值（0~1，仅保留高于该值的角点）
        minDistance=min_distance,     # 角点之间的最小欧氏距离
        useHarrisDetector=False       # 禁用 Harris 检测，使用纯 Shi-Tomasi 算法
    )
    # 复制原始图像用于绘制角点
    img_shi_tomasi = img.copy()
    if corners is not None:
        corners = np.int64(corners)
        for corner in corners:
            x, y = corner.ravel()
            cv2.circle(img_shi_tomasi, (x, y), 4, (0, 255, 0), -1)
    return img_shi_tomasi, corners

函数内部先调用cv2.goodFeaturesToTrack，禁用 Harris 检测模式，传入灰度图和角点数量、质量阈值等关键参数，获取筛选后的角点坐标。接着复制原始彩色图像避免修改原图，判断角点坐标非空后，将其转换为兼容新版本 NumPy 的整数格式，再通过循环遍历每个角点，用cv2.circle绘制绿色实心圆完成标记，最后返回标记好的结果图和角点坐标，既满足直观查看需求，也保留了原始角点数据供后续处理。

执行两种算法统一参数

python 复制代码

test_harris, _ = harris_corner_detect(test_img, test_gray)
test_shi_tomasi, _ = shi_tomasi_corner_detect(test_img, test_gray)

可视化

python 复制代码

plt.rcParams["figure.figsize"] = (16, 8)
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
plt.subplot(1, 2, 1)
plt.imshow(cv2.cvtColor(test_harris, cv2.COLOR_BGR2RGB))
plt.title("test1.jpg - Harris 角点检测（红色标记）")
plt.axis("off")
plt.subplot(1, 2, 2)
plt.imshow(cv2.cvtColor(test_shi_tomasi, cv2.COLOR_BGR2RGB))
plt.title("test1.jpg - Shi-Tomasi 角点检测（绿色标记）")
plt.axis("off")
plt.tight_layout()
plt.show()

二、结果分析

1. 红点多绿点少的原因

红点（Harris）多、绿点（Shi-Tomasi）少且看似"不全"，本质是两种算法的角点判定逻辑、筛选机制不同，Harris是"无差别标记高响应区域"，Shi-Tomasi是"精准筛选高质量角点"，并非Shi-Tomasi检测能力不足，而是它主动舍弃了低质量候选点。

2. 具体细节拆解

Harris红点多的原因：Harris通过阈值筛选全图像素的响应值，只要像素响应超过阈值就会被标记为红色，且没有"角点间最小距离"的限制，不仅会标记真正的角点，还会把纹理丰富的边缘、局部高对比度区域也标记出来，甚至同一角点周围的多个像素都会被同时标记，最终形成成片、密集的红点。
Shi-Tomasi绿点少且"不全"的原因 ：Shi-Tomasi有两层严格筛选，一是通过quality_level设定质量阈值，只保留特征值最小值较高的高质量角点，过滤掉边缘、低对比度区域的低质量候选点；二是通过max_corners（最大角点数）和min_distance（角点最小间距）做进一步限制，既不会超过设定的角点数量上限，也不允许角点在小范围内密集分布，主动舍弃了大量"冗余"和"低质量"点，所以绿点更少、更稀疏，看起来"不全"，但实际上是更精准的有效角点。

3. 总结

红点多是Harris无额外去重和质量筛选，标记了大量包含冗余、低质量区域的高响应像素；绿点少是Shi-Tomasi多层筛选，只保留高质量、非冗余的核心角点。
Shi-Tomasi的"不全"是相对Harris的"冗余标记"而言，并非漏检有效角点，反而这种"挑食"的特性让它更适合后续的特征匹配、光流跟踪等任务。

Ⅴ、角点检测算法在图像拼接的应用

在上一部分内容中，我们已经详细拆解了 Harris 角点检测的核心原理、实现逻辑以及它为何能成为计算机视觉中特征点提取的经典方案。理论的价值终究要落地到实战，而图像拼接正是 Harris 角点检测最直观、最实用的应用场景之一。

相比于单纯的角点提取，图像拼接需要将 Harris 角点检测与特征描述、特征匹配、单应性矩阵计算、图像融合等技术串联起来，形成一套完整的自动化流程。

python 复制代码

import cv2
import numpy as np
import matplotlib.pyplot as plt

plt.rcParams["font.sans-serif"] = ["SimHei"]  # 指定支持中文的黑体字体 
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示为方块的问题

def cv2_to_plt(img):
    """将 OpenCV BGR 格式图像转换为 Matplotlib 可显示的 RGB 格式"""
    if len(img.shape) == 3:  # 彩色图需要转换
        return cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
    else:  # 灰度图无需转换
        return img

# Harris 角点检测
def harris_corner_extract(gray_img, block_size=2, ksize=3, k=0.04, threshold=0.01):
    gray_float = np.float32(gray_img)
    harris_dst = cv2.cornerHarris(gray_float, blockSize=block_size, ksize=ksize, k=k)
    harris_dst = cv2.dilate(harris_dst, None)
    harris_thresh = threshold * harris_dst.max()
    corners = []
    h, w = gray_img.shape
    for y in range(h):
        for x in range(w):
            if harris_dst[y, x] > harris_thresh:
                kp = cv2.KeyPoint(x=float(x), y=float(y), size=10.0)
                corners.append(kp)
    return corners

# 两张图片拼接
def stitch_two_images(img1_path, img2_path):
    img1 = cv2.imread(img1_path)
    img2 = cv2.imread(img2_path)
    if img1 is None or img2 is None:
        raise Exception("图片读取失败！请检查图片路径是否正确，或图片格式是否支持（jpg/png 等）")
    gray1 = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
    gray2 = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)
    gray1_blur = cv2.GaussianBlur(gray1, (5, 5), 0)
    gray2_blur = cv2.GaussianBlur(gray2, (5, 5), 0)

    # 1. Harris 角点检测
    kp1 = harris_corner_extract(gray1_blur)
    kp2 = harris_corner_extract(gray2_blur)
    print(f"第一张图提取到 {len(kp1)} 个 Harris 角点")
    print(f"第二张图提取到 {len(kp2)} 个 Harris 角点")

    # 2. 用 ORB 算法为角点生成特征描述子（实现角点匹配）
    orb = cv2.ORB_create()
    kp1, des1 = orb.compute(gray1_blur, kp1)
    kp2, des2 = orb.compute(gray2_blur, kp2)

    # 3. 特征匹配：暴力匹配器筛选优质匹配点
    bf = cv2.BFMatcher(cv2.NORM_HAMMING, crossCheck=True)
    matches = bf.match(des1, des2)
    # 按匹配距离排序，取前 100 个优质匹配（距离越小，匹配度越高）
    matches = sorted(matches, key=lambda x: x.distance)[:100]

    # 4. 计算单应性矩阵（实现图像配准，RANSAC 算法去除异常匹配）
    pts1 = np.float32([kp1[m.queryIdx].pt for m in matches]).reshape(-1, 1, 2)
    pts2 = np.float32([kp2[m.trainIdx].pt for m in matches]).reshape(-1, 1, 2)
    H, mask = cv2.findHomography(pts2, pts1, cv2.RANSAC, 5.0)

    # 5. 图像变换与拼接：将 img2 映射到 img1 坐标空间，生成全景图
    h1, w1 = img1.shape[:2]
    h2, w2 = img2.shape[:2]
    # 计算拼接后图像的尺寸（避免内容被裁剪）
    img2_warped = cv2.warpPerspective(img2, H, (w1 + w2, h1))
    # 融合两张图像，完成拼接
    img2_warped[:h1, :w1] = img1
    # 优化：去除右侧多余的黑色背景（仅保留有效内容）
    stitch_result = img2_warped[:h1, :np.max(np.where(img2_warped.sum(axis=2) > 0)[1])]
    # 生成匹配结果可视化图
    match_img = cv2.drawMatches(img1, kp1, img2, kp2, matches[:50], None, flags=cv2.DrawMatchesFlags_NOT_DRAW_SINGLE_POINTS)
    
    return stitch_result, match_img, img1, img2  # 额外返回原图，方便可视化对比

#--------------------------------------------------------------------------------------------------------	

IMG_PATH_1 = "img1.jpg"
IMG_PATH_2 = "img2.jpg"
IMG_PATH_3 = "img3.jpg"
print("="*50)
print("开始执行 img1 与 img2 的拼接...")
try:
    stitch_12, match_12, img1, img2 = stitch_two_images(IMG_PATH_1, IMG_PATH_2)
    print("img1 与 img2 图像拼接成功！")
    plt.figure(figsize=(20, 12))
    plt.subplot(2, 2, 1)
    plt.imshow(cv2_to_plt(img1))
    plt.title("原图 img1", fontsize=14)
    plt.axis("off")
    plt.subplot(2, 2, 2)
    plt.imshow(cv2_to_plt(img2))
    plt.title("原图 img2", fontsize=14)
    plt.axis("off")
    plt.subplot(2, 2, 3)
    plt.imshow(cv2_to_plt(match_12))
    plt.title("img1 与 img2 角点匹配效果", fontsize=14)
    plt.axis("off")
    plt.subplot(2, 2, 4)
    plt.imshow(cv2_to_plt(stitch_12))
    plt.title("img1 与 img2 最终拼接结果", fontsize=14)
    plt.axis("off")
    plt.tight_layout() 
    plt.show()
except Exception as e:
    print(f"img1 与 img2 拼接出错：{e}")

python 复制代码

print("开始执行 img1 与 img3 的拼接...")
try:
    stitch_13, match_13, img1, img3 = stitch_two_images(IMG_PATH_1, IMG_PATH_3)
    print("img1 与 img3 图像拼接成功！")
    plt.figure(figsize=(20, 12))
    plt.subplot(2, 2, 1)
    plt.imshow(cv2_to_plt(img1))
    plt.title("原图 img1", fontsize=14)
    plt.axis("off")
    plt.subplot(2, 2, 2)
    plt.imshow(cv2_to_plt(img3))
    plt.title("原图 img3", fontsize=14)
    plt.axis("off")
    plt.subplot(2, 2, 3)
    plt.imshow(cv2_to_plt(match_13))
    plt.title("img1 与 img3 角点匹配效果", fontsize=14)
    plt.axis("off")
    plt.subplot(2, 2, 4)
    plt.imshow(cv2_to_plt(stitch_13))
    plt.title("img1 与 img3 最终拼接结果", fontsize=14)
    plt.axis("off")
    plt.tight_layout()
    plt.show()
except Exception as e:
    print(f"img1 与 img3 拼接出错：{e}")

Ⅵ、总结

在本次角点检测的系列分享中，我们从理论到实践，对 Harris 和 Shi-Tomasi 两种经典算法进行了全方位的拆解与验证，下面为你梳理核心的知识总结与对比：

一、核心知识总结

Harris 角点检测
- 本质：通过检测图像中局部窗口的灰度变化率，识别出在多个方向上都有显著变化的角点。
- 核心思想：利用二次型矩阵 M 描述窗口灰度变化，通过构造响应值 R 判断角点、边缘或平坦区域。
- 特点：角点提取数量充足，具备旋转不变性，但存在冗余角点和边缘误标，且不具备尺度不变性。
Shi-Tomasi 角点检测
- 本质：对 Harris 算法的改进，通过优化角点判定准则，提升角点质量和稳定性。
- 核心思想：用矩阵 M 的最小特征值代替 Harris 的响应值 R，仅保留最小特征值大于阈值的角点。
- 特点：提取的角点质量更高、冗余更少，在图像拼接等场景中鲁棒性更强，是工程上更常用的角点检测方案。
图像拼接中的应用
- 角点检测是图像拼接的核心前置步骤，通过提取重叠区域的稳定角点，为后续特征匹配、单应性矩阵计算和图像配准提供关键依据。
- 在实际项目中，Shi-Tomasi 通常是首选，而 Harris 可作为补充方案，用于纹理稀疏场景以增加角点数量。

二、算法横向对比

特性	Harris 角点检测	Shi-Tomasi 角点检测
角点质量	参差不齐，存在冗余和误标	质量高，精准度和稳定性更强
角点数量	数量充足，覆盖范围广	数量适中，无冗余
计算复杂度	较低，实现简单	略高，但工程收益更明显
工程实用性	适合对精度要求不高的场景	图像拼接、目标跟踪等主流场景首选

边缘检测：基础算子到高级边缘提取【计算机视觉】https://blog.csdn.net/R_Feynman_/article/details/157186376?spm=1001.2014.3001.5501

角点检测：Harris 与 Shi-Tomasi原理拆解【计算机视觉】

角点检测：Harris 与 Shi-Tomasi原理拆解【计算机视觉】

角点检测（Corner Detection）

Ⅰ、引言

Ⅱ、Harris 角点检测

一、Harris 角点检测的本质

二、Harris 角点检测算法数学原理

1. 定义窗口移动的灰度变化函数

2. 数学简化：一阶泰勒展开与二次型转化

3. 结构矩阵： M M M的性质与意义

4. 判断依据：Harris 响应值 R R R 构造

5. 核心判断：由 R R R 区分区域类型

6. 数学流程

Ⅲ、Shi-Tomasi 角点检测

一、Shi-Tomasi是对 Harris 角点理论的简化与改进

二、Shi-Tomasi的数学原理

1.核心思想

2. 数学定义

3. 区域分类直观解释

4. 与 Harris 角点的对比总结

5. 工程实现说明

Ⅳ、代码对比不同角点检测的结果

一、代码实现

二、结果分析

1. 红点多绿点少的原因

2. 具体细节拆解

3. 总结

Ⅴ、角点检测算法在图像拼接的应用

Ⅵ、总结

一、核心知识总结

二、算法横向对比

上一章