算法—字符串

最长公共前缀

最长回文子串

二进制求和

字符串相乘

最长公共前缀

**思路：**将所有字符串两两比较即可，先比较第一个和第二个，然后再将得到的公共前缀和第三个字符串进行比较，然后继续得到公共前缀，继续和下一个字符串进行比较。

代码：

cpp 复制代码

class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {
        string ret = strs[0];
        for(int i = 1; i < strs.size(); i++){
            ret = findCommon(ret, strs[i]);
        }

        return ret;
    }

    string findCommon(string& s1, string& s2){
        int n = min(s1.size(), s2.size());
        int i = 0;
        while(i < n && s1[i] == s2[i])
            i++;

        return s1.substr(0, i);
    }
};

最长回文子串

**思路：**使用中心扩展算法，首先固定一个中心点 i。然后从这个中心点开始，向两边拓展，假设向两边拓展的指针分别名为 left，right，因为最长的回文子串可能是奇数长度也可能是偶数长度，当它是奇数时，起始状态 i == left == right；当它是偶数时，起始状态 i == left，right = left + 1。

代码：

cpp 复制代码

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();
        int begin;
        int len = 0;
        int left, right;
        for(int i = 0; i < n; i++){
            left = right = i;
            while(left >= 0 && right < n && s[left] == s[right]){
                left--;
                right++;
            }
            if(right - left - 1 > len){
                begin = left + 1;
                len = right - left - 1;
            }

            left = i;
            right = i + 1;
            while(left >= 0 && right < n && s[left] == s[right]){
                left--;
                right++;
            }
            if(right - left - 1 > len){
                begin = left + 1;
                len = right - left - 1;
            }
        }

        return s.substr(begin, len);
    }
};

二进制求和

**思路：**定义两个指针分别指向两字符串末尾，定义一个变量存储进位，模拟加法的过程，只要两个字符串还有一个没有遍历完或者进位不为 0，循环就不能停止，因为还有数据需要往结果字符串中添加。需要注意的是，下面代码循环结束后得到的结果字符串不是最终结果，它其实是最终结果反过来了。

代码：

cpp 复制代码

class Solution {
public:
    string addBinary(string a, string b) {
        int i = a.size() - 1;
        int j = b.size() - 1;
        int carry = 0;
        string ret;
        while(i >= 0 || j >= 0 || carry != 0){
            if(i >= 0)
                carry += (a[i] - '0');
            if(j >= 0)
                carry += (b[j] - '0');

            ret += (carry % 2) + '0';
            carry /= 2;
            i--;
            j--;
        } 
        reverse(ret.begin(), ret.end());
        return ret;
    }
};

字符串相乘

**思路：**无进位相乘在相加，最后处理进位。将无进位相乘在相加的结果先存放在一个数组中，方便后面处理进位，将两个字符串反转，每次相乘的两个数的下标加和就是乘积应该存放的位置，处理进位的方式和字符串相加处理进位的方式相同，定义一个变量存放进位，然后遍历数组，将当前遍历的数加到进位中，取模 10 就是要加到结果字符串中的值，除以 10 就是下一轮循环的进位，进位一开始赋值 0。

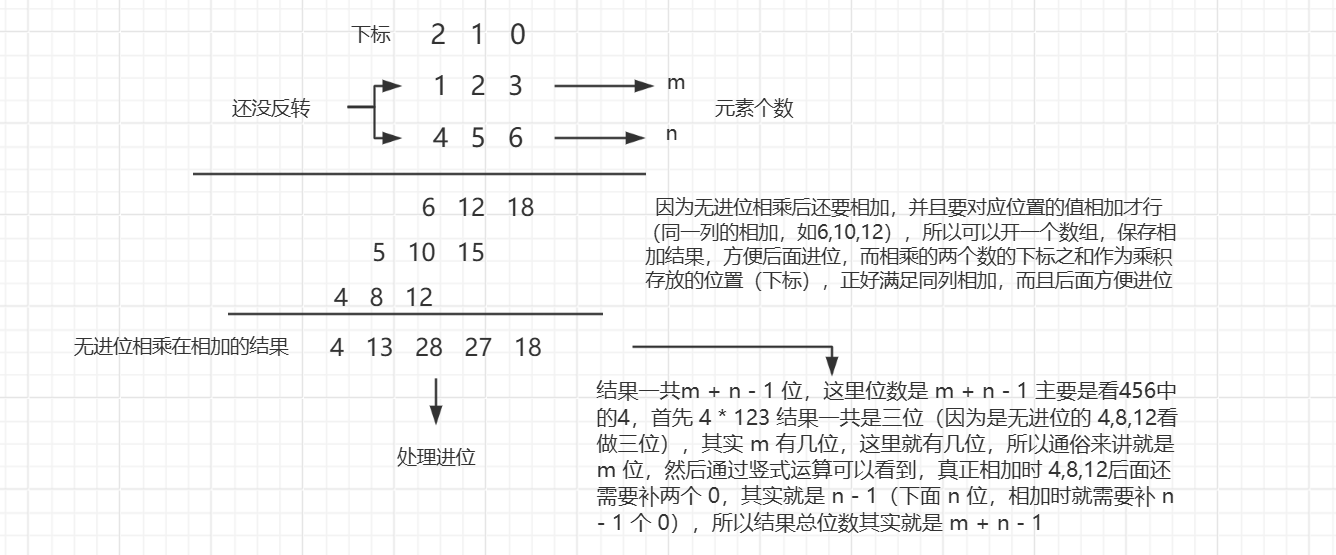
代码：

cpp 复制代码

class Solution {
public:
    string multiply(string num1, string num2) {
        int m = num1.size();
        int n = num2.size();
        reverse(num1.begin(), num1.end());
        reverse(num2.begin(), num2.end());
        vector<int> tmp(m + n - 1);

        //无进位相乘然后相加
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                tmp[i + j] += (num1[i] - '0') * (num2[j] - '0');
            }
        }

        //处理进位
        int cur = 0;
        int t = 0;
        string ret;
        while(cur < m + n - 1 || t != 0){
            if(cur < m + n - 1)
                t += tmp[cur++];
            ret += t % 10 + '0';
            t /= 10;
        }

        //处理前导零
        while(ret.size() > 1 && ret.back() == '0')
            ret.pop_back();

        reverse(ret.begin(), ret.end());
        return ret;
    }
};