Java实现常见算法

一、基础排序算法

排序算法是把一组数据按指定顺序（升 / 降）排列的算法，分简单排序 （入门，效率一般）和高效排序 （进阶，刷题 / 开发常用），重点记思路和适用场景，不用死记复杂优化。

1. 冒泡排序

Ⅰ.核心思路

像水里的气泡一样，大的数慢慢 "浮" 到数组末尾。重复遍历数组，每次比较相邻两个数，若顺序错了就交换，直到一轮遍历中没有交换发生（说明已经有序）。

Ⅱ.适用场景

数据量极小（几十条）、对效率要求不高，纯入门理解排序思想。

Ⅲ.代码实现：

Ⅳ.小贴士

• 冒泡排序是稳定排序（相同数的相对顺序不变）；
• 核心特点：每轮确定一个最大数的位置。

2. 选择排序

Ⅰ.核心思路

每次从未排序的部分找最小（大）的数 ，放到未排序部分的起始位置，直到所有数都排好。

Ⅱ.适用场景

数据量小，想减少交换次数（比冒泡少很多交换，只有找到最值时才交换）。

Ⅲ.代码实现

Ⅳ.小贴士

• 选择排序是不稳定排序（比如数组 2, 2, 1，第一个 2 会和 1 交换，两个 2 的相对顺序变了）；
• 核心特点：每轮确定一个最小值的位置，交换次数远少于冒泡。

3. 插入排序

Ⅰ.核心思路

像打扑克牌理牌一样，把每个数依次插入到前面已经排好序的合适位置，前面的数始终是有序的，直到所有数插入完成。

Ⅱ.适用场景

数据量小，或数据本身接近有序（此时效率极高，接近 O (n)）。

Ⅲ.代码实现

Ⅳ.小贴士

• 插入排序是稳定排序；
• 小白最容易理解的排序，因为和手动理牌逻辑完全一致。

4. 快速排序

Ⅰ.核心思路

分治思想（把大问题拆成小问题解决）：

1. 选一个数当基准数（比如数组第一个数、最后一个数）；
2. 把数组分成两部分：左边都比基准小，右边都比基准大（这个过程叫「分区」）；
3. 对左边和右边的子数组重复上述步骤，直到子数组只有一个数（天然有序）。

Ⅱ.适用场景

绝大多数场景 （数据量中等 / 大），是 Java 集合中Arrays.sort()的底层算法之一。

Ⅲ.代码实现

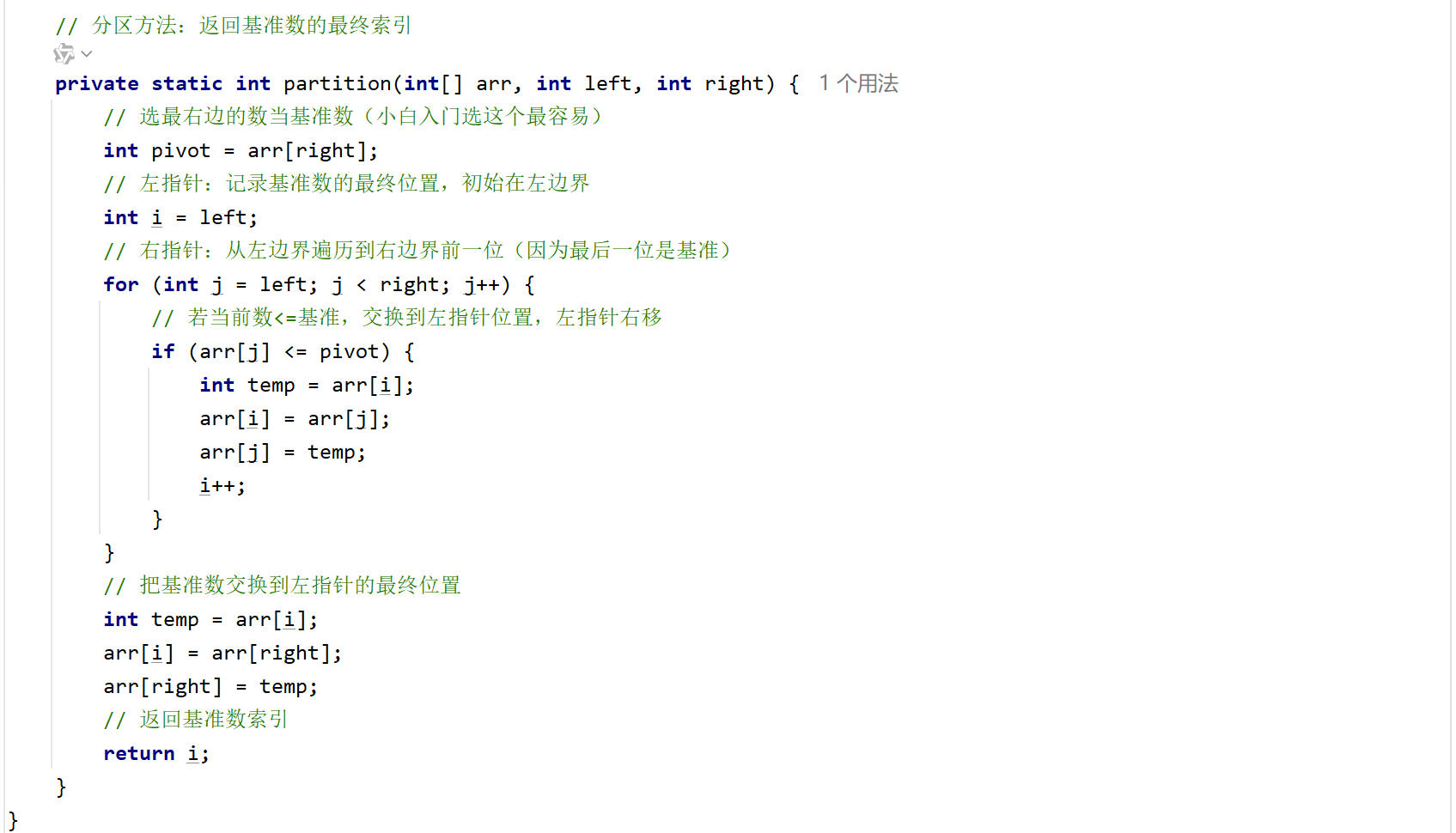
Ⅳ.小贴士

• 快速排序是不稳定排序；
• 平均效率极高（时间复杂度 O (nlogn)），最坏情况（数组已完全有序）是 O (n²)，但日常使用几乎遇不到；
• 不用死记代码，重点理解「分治 + 分区」的核心思想。

5. 归并排序

Ⅰ.核心思路

分治思想 + 合并有序数组：

1. 分：把数组从中间拆成两个子数组，再继续拆，直到子数组只有一个数；
2. 治 ：把两个有序的子数组合并成一个更大的有序数组；
3. 重复拆分和合并，最终得到完整的有序数组。

Ⅱ.适用场景

数据量极大、要求稳定排序 ，或链表排序（归并排序对链表更友好，无需额外空间）。

Ⅲ.代码实现

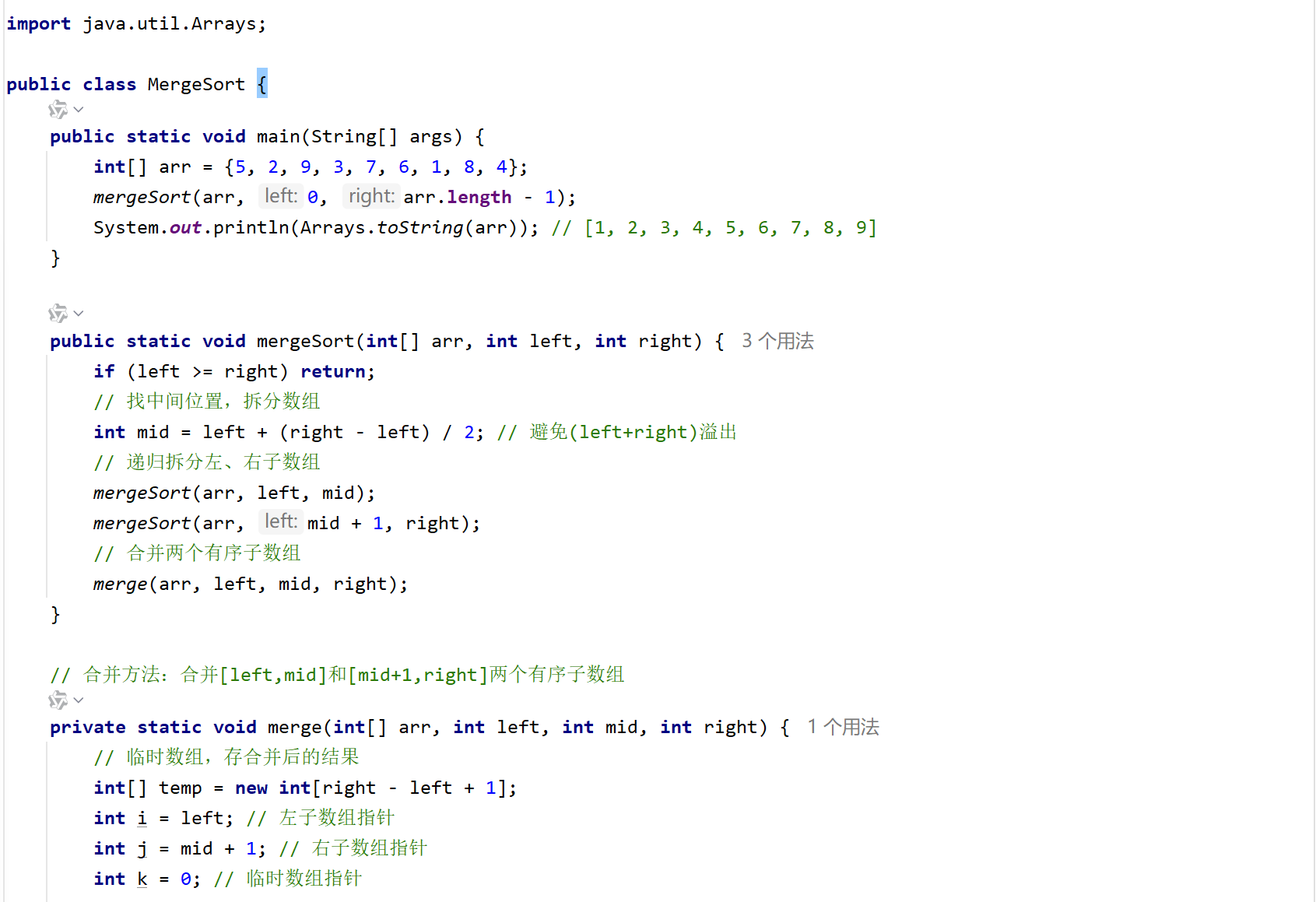
Ⅳ.小贴士

• 归并排序是稳定排序，时间复杂度始终 O (nlogn)（最坏 / 最好都一样）；
• 缺点：需要额外的临时数组，占用更多内存。

6.排序算法小白速记表

算法	时间复杂度 （平均）	稳定性	适用场景	核心特点
冒泡排序	O(n²)	稳定	数据量极小	相邻比较，大值后移
选择排序	O(n²)	不稳定	数据量小，减少交换	找最值，放到起始位置
插入排序	O(n²)	稳定	数据量小 / 接近有序	逐个插入有序部分
快速排序	O(nlogn)	不稳定	绝大多数场景（主力）	分治 + 分区，效率最高
归并排序	O(nlogn)	稳定	大数据 / 链表 / 要求稳定	分治 + 合并有序数组

结论 ：日常刷题 / 开发，优先用快速排序 ；要求稳定排序用归并排序；数据量极小随便用前三个简单排序。

二、基础查找算法

查找算法是从一组数据中找到指定值的位置 （或判断是否存在），分顺序查找 （入门）和二分查找（高效，重点）。

1. 顺序查找

Ⅰ.核心思路

从数组第一个数开始，逐个遍历，直到找到目标值或遍历结束。

Ⅱ.适用场景

任意数据（有序 / 无序都可以），数据量小。

Ⅲ.代码实现

Ⅳ.小贴士

• 无需预处理数据，直接遍历；
• 效率低（O (n)），数据量大时千万别用。

2. 二分查找

Ⅰ.核心思路

前提 ：数据必须是有序的 （升 / 降）！每次取中间位置的数和目标值比较，缩小查找范围：

1. 中间数 **==**目标值：找到，返回索引；
2. 中间数**>** 目标值：目标值在左半部分，缩小右边界；
3. 中间数**<** 目标值：目标值在右半部分，缩小左边界；重复上述步骤，直到找到目标值或查找范围消失（没找到）。

Ⅱ.适用场景

有序数组 / 集合，数据量中等 / 大（刷题 / 开发最常用）。

Ⅲ.代码实现

Ⅳ.小贴士

• 二分查找效率极高（时间复杂度 O (logn)），比如找 100 万个数中的一个，最多只需要 20 次比较；
• 核心前提：数据必须有序！无序数组用二分查找必错；
• 别用mid = (left+right)/2，当 left 和 right 很大时会整数溢出 ，用left + (right-left)/2更安全。

三、递归算法

递归是必懂的算法思想，很多复杂算法（快速排序、归并排序、斐波那契）都基于递归，核心是「自己调自己」。

Ⅰ.核心思路

把大问题拆成和原问题相似的小问题，解决小问题后，大问题自然解决，包含两个关键部分：

1. 递归递推：大问题拆成小问题，调用自身；
2. 递归终止条件 ：当小问题简单到可以直接解决时，停止递归（必须有，否则会无限递归导致栈溢出）。

Ⅱ.适用场景

问题可以拆分成相似的子问题（如排序、斐波那契、阶乘、迷宫问题）。

Ⅲ.代码实现

案例 1：求 n 的阶乘

**提示：**n! = 1×2×3×...×n，0! = 1! = 1

案例 2：斐波那契数列

**提示：**1,1,2,3,5,8,13...，第 n 项 = 第 n-1 项 + 第 n-2 项

Ⅳ.小贴士

• 递归的优点 ：代码简洁，思路清晰；缺点：占用栈内存，重复计算（如斐波那契）；
• 写递归的第一步：先想终止条件，再想递推公式，别先写递推；
• 遇到重复计算问题（如斐波那契），可以用数组 / HashMap 缓存计算结果（小白后期再学）。

四、其他必知的简单算法

1. 斐波那契数列

2. 阶乘

3. 求数组最大/小值

五、学习算法的核心技巧

1. 先理解思路，再写代码：别死记硬背代码，比如快速排序，先想「分治 + 分区」，再慢慢敲代码，忘的时候能根据思路重新写
2. 从简单到复杂：先掌握冒泡、选择、插入、顺序查找，再学快速排序、二分查找，最后学递归和归并排序，别一步登天
3. 多敲代码，少看代码 ：看 10 遍不如敲 1 遍，敲的时候故意卡壳，想清楚每一步的作用，比如二分查找的mid怎么算、边界怎么缩
4. 用小数据测试：写好算法后，用小数组（如 3-5 个数）手动走一遍流程，看是否和代码执行结果一致，比如冒泡排序，手动模拟每轮的交换过程
5. 别纠结优化，先实现基础功能：开始阶段不用管快速排序的基准数怎么选更优、归并排序怎么省内存，先把基础版本写对、跑通
6. 结合场景记算法：比如 "有序数组找数" 就想到二分查找，"排序数据量大数据" 就想到快速排序，"要求稳定排序" 就想到归并排序

六、Java 中算法的实际应用

1. 数组排序 ：直接用Arrays.sort(arr)，底层是快速排序 + 归并排序，比自己写的排序更高效
2. 集合查找 ：ArrayList的indexOf()是顺序查找 ，TreeSet/TreeMap的查找是二分查找（因为底层是有序的红黑树）
3. 字符串查找 ：String的indexOf()是基于暴力匹配的顺序查找

总结

开始阶段的 Java 算法核心就围绕 「排序 + 查找 + 递归」 三大块，要重点掌握：

1. 简单排序（冒泡 / 选择 / 插入）理解思想，高效排序（快速 / 归并）会写基础实现、知道适用场景
2. 二分查找的有序前提 和边界收缩，能写非递归版
3. 递归的终止条件 + 递推公式，会写阶乘、斐波那契的递归和非递归版
4. 所有算法先实现基础功能，再考虑优化，多敲多练是关键