目录
[🔹 移动零(283)](#🔹 移动零(283))
[🔹 复写零(1089)](#🔹 复写零(1089))
[🔹 快乐数(202)](#🔹 快乐数(202))
[💡 刷题总结](#💡 刷题总结)
最近刷了三道经典的算法题,分别是「移动零」「复写零」和「快乐数」,每一道都有巧妙的解题思路。我想把这些思路和对应的代码实现记录下来,也算是一次探索性学习的总结。
🔹 移动零(283)
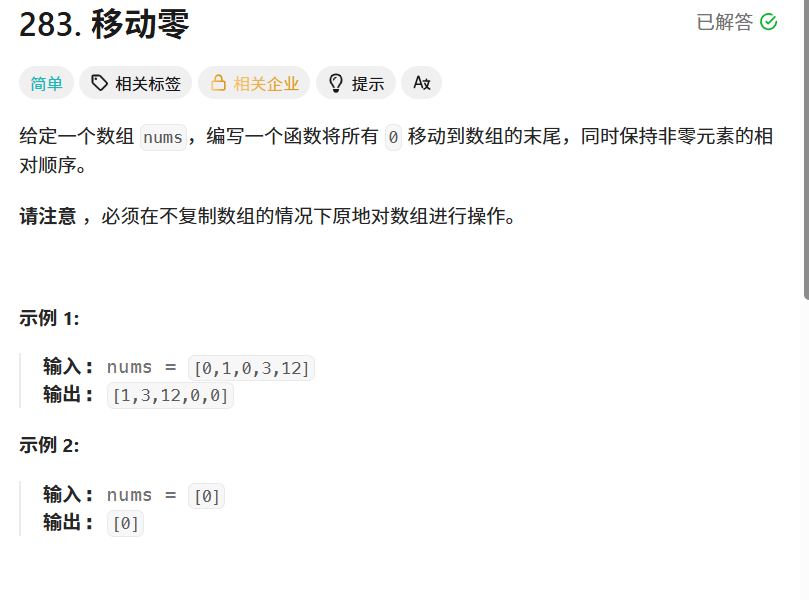
题目要求
把数组里所有的 0 移动到末尾,同时保持非零元素的相对顺序,必须原地操作。
核心思路
这是一个典型的双指针问题:
left指针:指向当前可以放置非零元素的位置(初始为-1)right指针:遍历整个数组- 当
right遇到非零元素时,就和left+1位置的元素交换,这样保证了非零元素的顺序,也把0挤到了后面
代码实现
cpp
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int left = -1, right = 0;
while (right < nums.size()) {
if (nums[right] == 0) {
right++;
} else {
swap(nums[++left], nums[right++]);
}
}
}
};探索思考
这道题的关键是理解 "原地操作" 的含义。如果允许使用额外数组,直接把非零元素存进去再补零就可以了,但双指针的方法让空间复杂度降到了 O(1),是最优解。
🔹 复写零(1089)

题目要求
遍历数组,遇到 0 就把它复写一遍,后面的元素右移,且不能超过数组长度。
核心思路
这道题的难点在于如果直接从前往后复写,会覆盖掉还没处理的元素。所以我们用两次遍历的思路:
- 第一次遍历 :用
cur和dest两个指针,计算出最终每个元素的目标位置,找到最后一个需要保留的元素。 - 第二次遍历 :从后往前复写,这样就不会覆盖未处理的元素。如果最后一个元素是
0且刚好超出数组长度,需要单独处理。
代码实现
cpp
class Solution {
public:
void duplicateZeros(vector<int>& arr) {
int cur = 0, dest = -1;
int n = arr.size();
// 第一次遍历:找到最终的位置
while (cur < n) {
if (arr[cur]) dest++;
else dest += 2;
if (dest >= n - 1) break;
cur++;
}
// 处理边界情况:最后一个0复写后超出数组
if (dest == n) {
arr[n - 1] = 0;
cur--;
dest -= 2;
}
// 第二次遍历:从后往前复写
while (cur >= 0) {
if (arr[cur]) {
arr[dest--] = arr[cur--];
} else {
arr[dest--] = 0;
arr[dest--] = 0;
cur--;
}
}
}
};探索思考
从后往前的逆向思维是这道题的精髓。如果正向操作,每次遇到 0 都要移动后面的元素,时间复杂度会达到 O(n²),而两次遍历的方法把时间复杂度降到了 O(n),非常高效。
🔹 快乐数(202)

题目要求
判断一个数是不是快乐数:反复计算各位数字的平方和,最终如果能得到 1 就是快乐数,否则会进入无限循环。
核心思路
这道题的关键是如何判断 "无限循环"。我们可以用 ** 快慢指针(Floyd 判圈算法)** 来检测循环:
slow指针:每次计算一次平方和fast指针:每次计算两次平方和- 如果存在循环,
fast最终会追上slow;如果是快乐数,slow会先到达1
代码实现
cpp
class Solution {
public:
int bitsum(int n) {
int sum = 0;
while (n) {
sum += pow(n % 10, 2);
n = n / 10;
}
return sum;
}
bool isHappy(int n) {
int slow = n, fast = bitsum(n);
while (slow != fast) {
slow = bitsum(slow);
fast = bitsum(bitsum(fast));
}
return slow == 1;
}
};探索思考
这道题也可以用哈希表来记录已经出现过的数字,但快慢指针的方法不需要额外空间,空间复杂度是 O(1)。而且判圈算法在很多链表问题中也会用到,是一个非常通用的技巧。
💡 刷题总结
这三道题虽然看起来不同,但都用到了双指针的核心思想:
- 移动零:同向双指针,一个负责找非零元素,一个负责放置
- 复写零:两次遍历,正向找位置,逆向写元素
- 快乐数:快慢指针,检测循环
探索性学习的乐趣就在于,你会发现很多看似无关的问题,背后都有相通的解题思路。多总结、多思考,才能真正把算法内化成自己的能力。