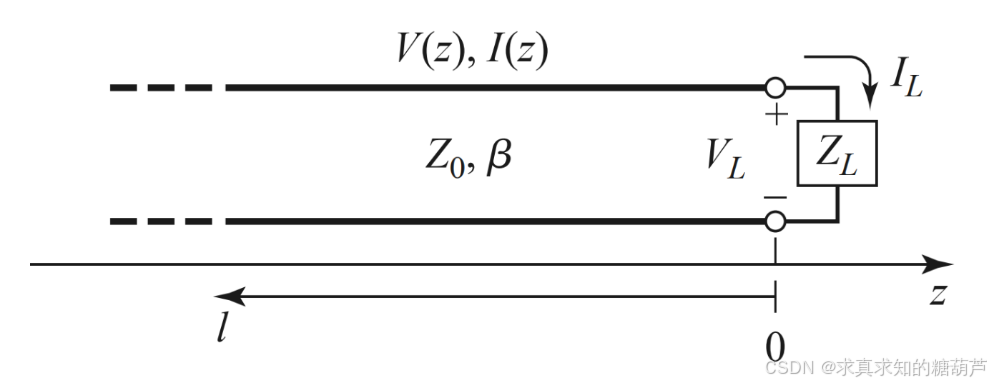
上一节我们通过开路短路法求解了传输线特性阻抗Z0Z_0Z0 ,这一节我们来求解电长度βl\beta lβl
传输线阻抗方程 描述了当特征阻抗为 Z0Z_0Z0 的传输线终端连接负载 ZLZ_LZL 时,输入阻抗 ZinZ_{in}Zin 的表达式:
Zin=Z0ZL+jZ0tan(βl)Z0+jZLtan(βl)(1) Z_{in} = Z_0 \frac{Z_L + j Z_0 \tan(\beta l)}{Z_0 + j Z_L \tan(\beta l)} \tag{1} Zin=Z0Z0+jZLtan(βl)ZL+jZ0tan(βl)(1)
其中
- Z0Z_0Z0:传输线特征阻抗(Ω)
- ZLZ_LZL:负载阻抗(Ω)
- lll:传输线长度(m)
- β\betaβ:相位常数,β=2πλ\beta = \frac{2\pi}{\lambda}β=λ2π(rad/m)
从传输线阻抗方程出发:
Zin=Z0ZL+jZ0tan(βl)Z0+jZLtan(βl) Z_{in} = Z_0 \frac{Z_L + j Z_0 \tan(\beta l)}{Z_0 + j Z_L \tan(\beta l)} Zin=Z0Z0+jZLtan(βl)ZL+jZ0tan(βl)
我们将负载短路,然后传输线另外一段接个port求Zin即可求解我们想求的电长度了。
βl=arctan(ZinsjZ0)+nπ,n=0,±1,±2,... \beta l = \arctan\left( \frac{Z_{in_s}}{j Z_0 } \right) + n\pi, \quad n = 0, \pm1, \pm2, ... βl=arctan(jZ0Zins)+nπ,n=0,±1,±2,...
下面我们用ADS里的微带线模型MLIN来验证
首先我们打开ADS,新建原理图
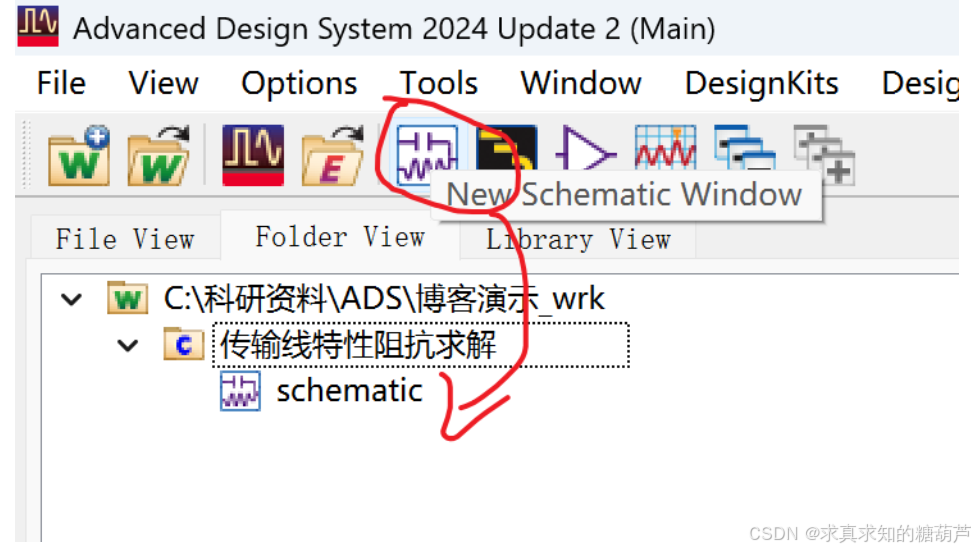
接下来我们打开lineCalc,
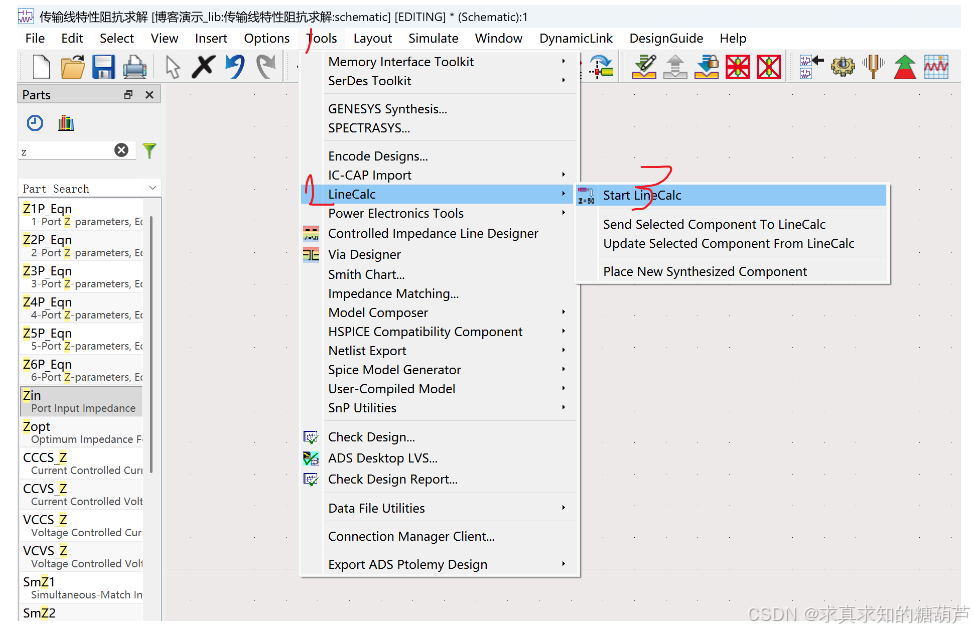
选择左上角Component为MLIN,然后设置好衬底参数,还有特性阻抗Z0Z_0Z0(主要取决于微带线宽度w)和电长度--这里设置成90°(取决于微带线长度L),最后我这里设置左下角仿真频率为5GHz。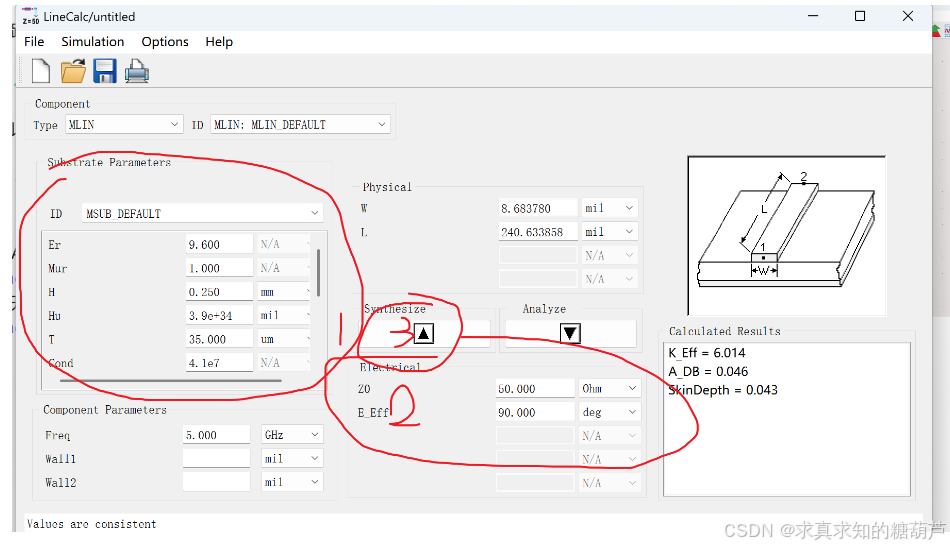
下面按照相应的衬底参数搭建好对应原理图(注意衬底参数要和刚刚计算的MSUB衬底参数一致,把传输线参数输入,同时放入两个Zinport,修改一下第二个port为S22,PortZ2)
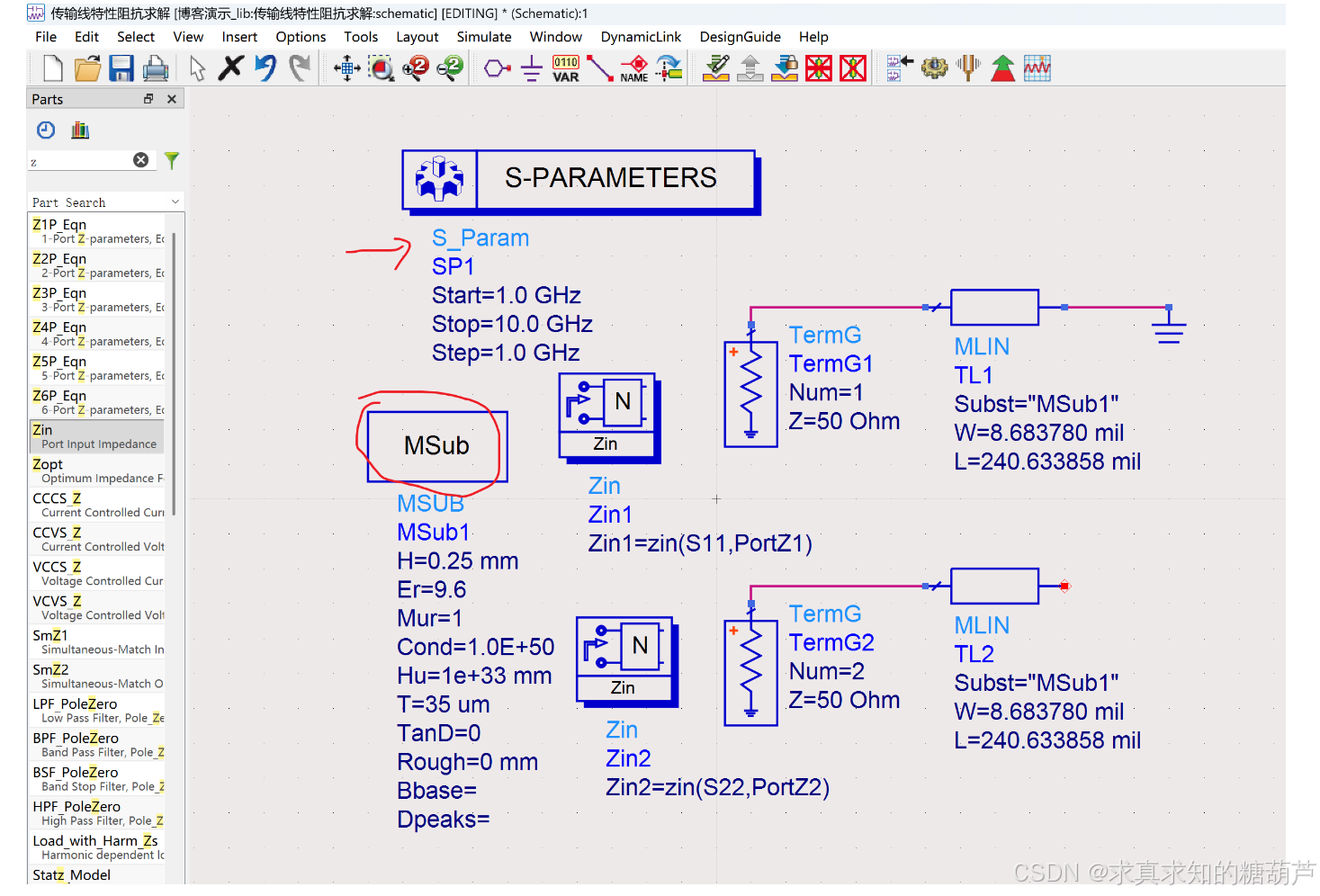
开始仿真,在弹出的界面输入以下公式即可得到结果,可以看到5Ghz下电长度为90°符合我们设置
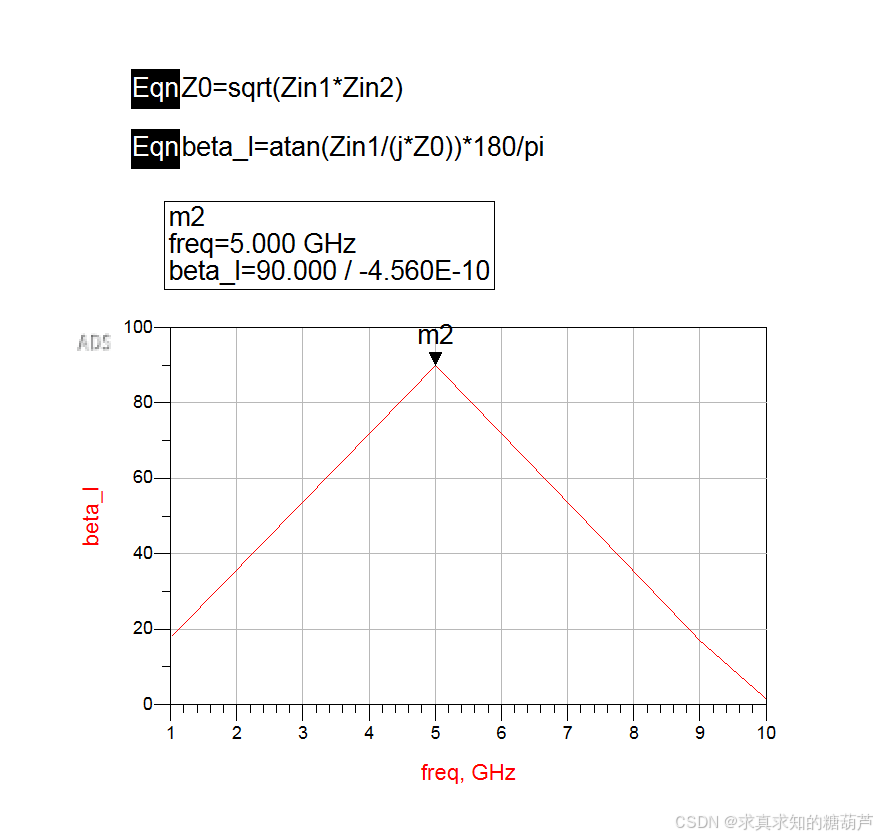
刚刚lineCalc预设得到的一致。实际的版图上的传输线同样也可以通过这种方法联合仿真求特征阻抗。