【刘二大人】PyTorch深度学习实践笔记 —— 第三集：梯度下降（凝练版）

文章目录

- - [1. 为什么要引入梯度下降？（前期铺垫）](#1. 为什么要引入梯度下降？（前期铺垫）)
  - [2. 梯度下降算法的核心概念（先拿 w w w举例，其实还有 b b b的梯度下降）](#2. 梯度下降算法的核心概念（先拿 w w w举例，其实还有 b b b的梯度下降）)
  - [3. 深度学习中的特殊陷阱：鞍点（Saddle Point）](#3. 深度学习中的特殊陷阱：鞍点（Saddle Point）)
  - [4. 数学推导（MSE的梯度）](#4. 数学推导（MSE的梯度）)
  - - （1）通用的求导套路（链式法则）
    - （2）分别推导三个参数的梯度
    - [（3）总结与代码实现的直觉](#（3）总结与代码实现的直觉)
    - [（4）合成矩阵计算和拆开计算结果相同](#（4）合成矩阵计算和拆开计算结果相同)
    - [（5）更新公式（The Update Rule）](#（5）更新公式（The Update Rule）)
  - [5.小批量梯度下降（Mini-Batch GD）](#5.小批量梯度下降（Mini-Batch GD）)
  - [6. 性能对比与最终方案：Mini-Data Batch](#6. 性能对比与最终方案：Mini-Data Batch)
  - - [（1）并行计算能力 (Parallel Computation)](#（1）并行计算能力 (Parallel Computation))
    - （2）时间复杂度 (Time Complexity)
    - （3）工程实践中的关键限制
    - 最终方案选择：Mini-Batch
  - [7. 实战举例：10个房价样本的手算训练过程](#7. 实战举例：10个房价样本的手算训练过程)
  - - [（1）准备工作（Data & Model）](#（1）准备工作（Data & Model）)
    - [（2）训练过程：第一个 Mini-Batch 的诞生](#（2）训练过程：第一个 Mini-Batch 的诞生)
    - [（3）见证奇迹：完整跑完第二个 Mini-Batch](#（3）见证奇迹：完整跑完第二个 Mini-Batch)
    - （4）底层逻辑总结
    - （5）终局：什么时候才算"训练完成"？
  - [8. 代码复现（对应上述手算过程）](#8. 代码复现（对应上述手算过程）)
  - - 代码输出结果对照：
  - [9. 梯度下降的本质](#9. 梯度下降的本质)
  - [10. 深度答疑：直击灵魂的三个追问](#10. 深度答疑：直击灵魂的三个追问)
  - - Q1：梯度下降容易陷入局部最优吗？鞍点又是怎么回事？（高维空间的真相）
    - Q2：既然这么多坑，这些都不是问题吗？
    - Q3：每个参数都到了"低点"（偏导为0），怎么能证明合起来就是全维度的最低点？
    - [Q4：怎么理解"虽然表面上我们是用 Loss 分别计算每个参数的偏导，但参数之间其实是紧密耦合的"](#Q4：怎么理解“虽然表面上我们是用 Loss 分别计算每个参数的偏导，但参数之间其实是紧密耦合的”)
    - [1. 如果它们"各玩各的"（互相不理）](#1. 如果它们“各玩各的”（互相不理）)
    - [2. 它们"互相耦合"的真相](#2. 它们“互相耦合”的真相)
  - 核心结论
  - 11.总结课程的逻辑链

这一讲的核心主题是 梯度下降算法（Gradient Descent） ，它是深度学习中最基础但也最重要的优化方法。

1. 为什么要引入梯度下降？（前期铺垫）

回顾上一讲的笨办法 ：上一讲用的是"穷举法"，即在一个范围内把所有可能的权重 w w w 都试一遍，画出图像找最低点。
穷举法的致命缺陷（维度灾难）：
- 如果只有一个权重 w w w，画个曲线还能找。
- 如果有两个权重（ w 1 , w 2 w_1, w_2 w1,w2），搜索空间是平面的，搜索量是 100 × 100 100 \times 100 100×100。
- 如果有10个权重，搜索量是 100 10 100^{10} 10010。深度神经网络动辄数百万参数（如AlexNet有5000万参数），穷举法完全不可行。
分治法（Divide and Conquer）的局限性：
- 即便采用"先粗搜、再细搜"的策略，该方法仍要求损失函数曲面具备规则特性（如凸函数性质）。
分治法的典型失效场景：

第一步（粗搜 ）：以5米为间隔进行采样。

不幸情况：目标井仅1米宽，采样间隔却达5米。

某次采样恰好落在井左侧（高地），下一次则落在右侧（高地），采样点直接"跨越"了真正的最低点。

同时，另一个采样点落在足球场内，测得该区域比周边都低。

第二步（错误推断）：算法比较采样数据后，得出"足球场区域读数最低"的结论，并断言："最优解在足球场方向，井区域都是高地，无需考虑。"

第三步（细搜）：将所有计算资源集中在足球场及周边区域进行精细搜索。

结果：无论搜索多么细致，最终只能找到足球场的草皮（局部最优解），而真正的宝藏（深井）因初始采样遗漏，永远无法被发现。
- 非凸（Non-Convex）问题 ：深度学习中的损失函数曲面结构复杂，存在大量局部极值，分治法极易陷入错误的局部区域，难以找到全局最优解。

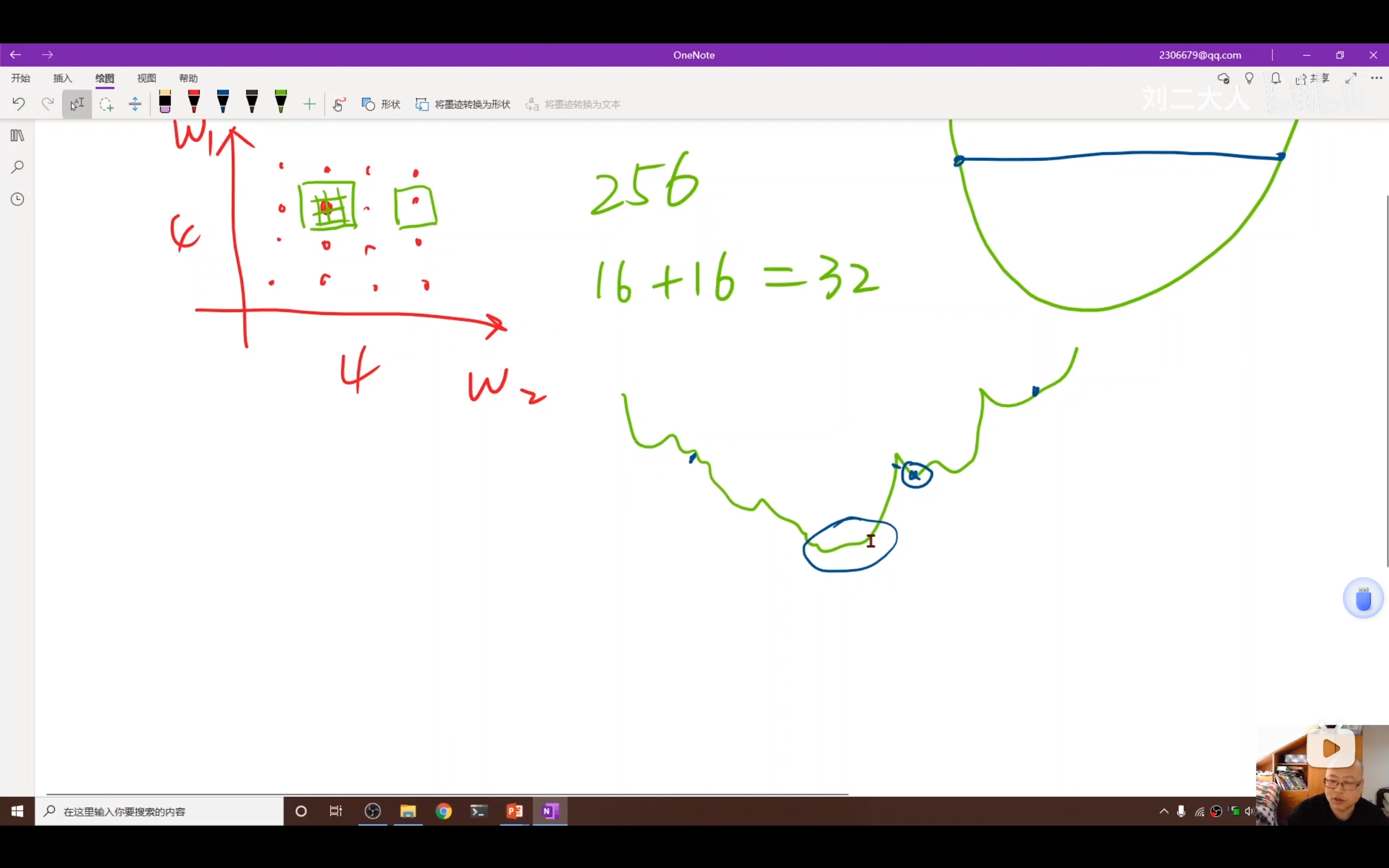
2. 梯度下降算法的核心概念（先拿 w w w举例，其实还有 b b b的梯度下降）

先举例 w w w的梯度下降：

优化问题（Optimization Problem）：目标是找到一组权重，使成本函数（Cost Function）的值最小。
贪心思想 ：梯度下降本质上是一种贪心算法（Greedy Algorithm）。它不看全局，只看眼前，每一步都朝着当前下降最快的方向走。
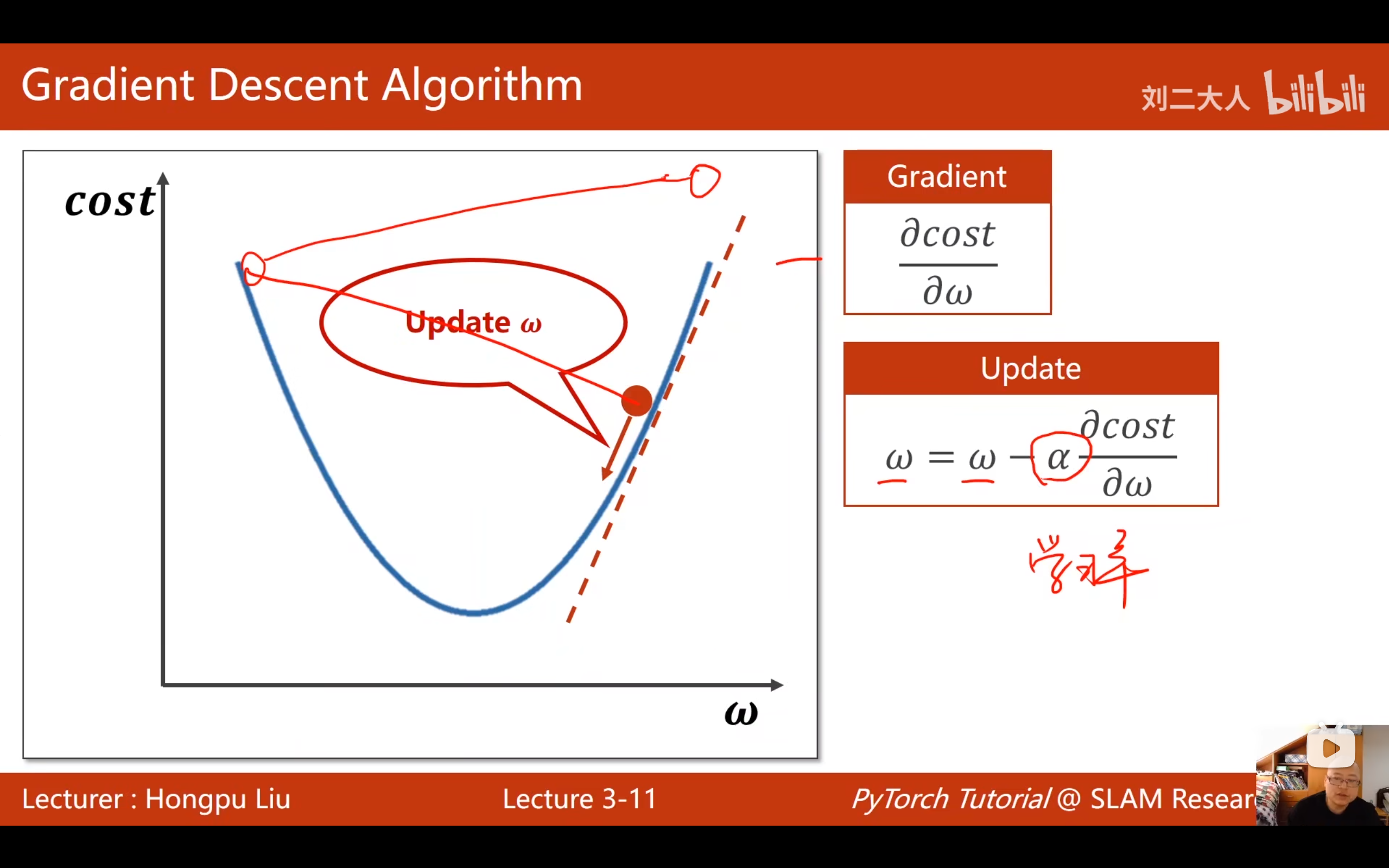
梯度的物理意义 ：
- 导数正负：导数为正表示函数在上升，导数为负表示函数在下降。
- 更新公式 ：为了让函数值变小（下山），我们要往梯度的反方向走。
- 公式： w = w − α ⋅ ∂ C o s t ∂ w w = w - \alpha \cdot \frac{\partial Cost}{\partial w} w=w−α⋅∂w∂Cost （其中 α \alpha α 是学习率）。
局部最优（Local Minima）与全局最优（Global Minima） ：
- 梯度下降只能保证到达局部最优，不能保证全局最优。
- 非凸函数 ：在非凸函数上，从不同起点出发，可能会陷入不同的局部低谷。

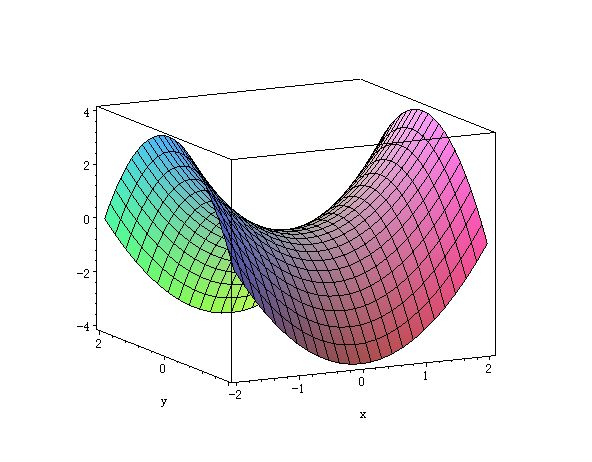
3. 深度学习中的特殊陷阱：鞍点（Saddle Point）

刘二大人特别强调，在深度学习中，真正让你头疼的往往不是局部最小值，而是鞍点。
什么是鞍点 ：梯度为0的点（停滞不前），但它既不是最大值也不是最小值。
- 比如马鞍形状：在前后方向看是最小值，在左右方向看是最大值。
原因：在高维空间（涉及成千上万个参数，远不止 w 1 w1 w1和 b b b两个）中，损失函数的结构异常复杂。某个点在 w w w维度上可能处于最低点（波谷），但在其他维度（如 b b b或其他 w 2 w2 w2参数）上却表现为最高点（波峰）。当这种**"谷峰并存"**的特征同时出现时，就形成了鞍点。
后果：由于梯度为0，更新公式中的 Δ w \Delta w Δw 变为0，参数停止更新，网络"以为"自己找到了最优解，实际上只是卡在了半山腰。

4. 数学推导（MSE的梯度）

举例来说，输入数据是二维的，每个样本包含两个特征 x 1 x_1 x1 和 x 2 x_2 x2。以房价预测为例， y y y 表示房价， x 1 x_1 x1 代表房屋面积， x 2 x_2 x2 表示地理位置。这种情况下，模型将由三个参数 ( w 1 w_1 w1, w 2 w_2 w2, b b b) 组成，如下表所示。

样本序号 ( n n n)	x 1 x_1 x1 (面积, 平米)	x 2 x_2 x2 (地段评分, 1-10)	y y y (真实房价, 万元)
1	80	2 (郊区)	200
2	100	2 (郊区)	240
3	80	8 (市中心)	500
4	120	5 (近郊)	400
5	150	9 (核心区)	900

此时的模型预测公式变为：
y ^ = w 1 ⋅ x 1 + w 2 ⋅ x 2 + b \hat{y} = w_1 \cdot x_1 + w_2 \cdot x_2 + b y^=w1⋅x1+w2⋅x2+b

损失函数（MSE）依然是：
C o s t = 1 N ∑ n = 1 N ( y ^ n − y n ) 2 Cost = \frac{1}{N} \sum_{n=1}^{N} (\hat{y}_n - y_n)^2 Cost=N1n=1∑N(y^n−yn)2

代入 y ^ n \hat{y}n y^n 后：
C o s t = 1 N ∑ n = 1 N ( w 1 x n , 1 + w 2 x n , 2 + b − y n ) 2 Cost = \frac{1}{N} \sum{n=1}^{N} (w_1 x_{n,1} + w_2 x_{n,2} + b - y_n)^2 Cost=N1n=1∑N(w1xn,1+w2xn,2+b−yn)2

我们需要分别对这三个参数求偏导数（梯度）。

（1）通用的求导套路（链式法则）

为了简化，我们设括号内部的一大坨为 z n z_n zn（残差项）：
z n = w 1 x n , 1 + w 2 x n , 2 + b − y n z_n = w_1 x_{n,1} + w_2 x_{n,2} + b - y_n zn=w1xn,1+w2xn,2+b−yn

那么单个样本的损失就是 L o s s n = z n 2 Loss_n = z_n^2 Lossn=zn2。

链式法则公式 ：
∂ L o s s ∂ 参数 = ∂ L o s s ∂ z × ∂ z ∂ 参数 \frac{\partial Loss}{\partial \text{参数}} = \frac{\partial Loss}{\partial z} \times \frac{\partial z}{\partial \text{参数}} ∂参数∂Loss=∂z∂Loss×∂参数∂z

我们知道外层导数（对平方求导）永远是：
∂ L o s s ∂ z = 2 ⋅ z n = 2 ⋅ ( y ^ n − y n ) \frac{\partial Loss}{\partial z} = 2 \cdot z_n = 2 \cdot (\hat{y}_n - y_n) ∂z∂Loss=2⋅zn=2⋅(y^n−yn)

这一部分是所有参数共有的。

（2）分别推导三个参数的梯度

对 w 1 w_1 w1 的梯度
∂ C o s t ∂ w 1 = 1 N ∑ n = 1 N 2 ( y ^ n − y n ) ⏟ 外层 ⋅ ∂ z n ∂ w 1 ⏟ 内层 \frac{\partial Cost}{\partial w_1} = \frac{1}{N} \sum_{n=1}^{N} \underbrace{2(\hat{y}n - y_n)}{\text{外层}} \cdot \underbrace{\frac{\partial z_n}{\partial w_1}}_{\text{内层}} ∂w1∂Cost=N1n=1∑N外层 2(y^n−yn)⋅内层 ∂w1∂zn

看 z n z_n zn 的公式： w 1 x n , 1 + w 2 x n , 2 + b − y n w_1 x_{n,1} + w_2 x_{n,2} + b - y_n w1xn,1+w2xn,2+b−yn。
对 w 1 w_1 w1 求导时， w 2 , b , y n w_2, b, y_n w2,b,yn 都是常数，消掉了。只剩下 w 1 x n , 1 w_1 x_{n,1} w1xn,1，系数是 x n , 1 x_{n,1} xn,1。
结果：
∂ C o s t ∂ w 1 = 1 N ∑ n = 1 N 2 ⋅ x n , 1 ⋅ ( y ^ n − y n ) \frac{\partial Cost}{\partial w_1} = \frac{1}{N} \sum_{n=1}^{N} 2 \cdot x_{n,1} \cdot (\hat{y}_n - y_n) ∂w1∂Cost=N1n=1∑N2⋅xn,1⋅(y^n−yn)

对 w 2 w_2 w2 的梯度

同理，对 w 2 w_2 w2 求导时，内层的导数系数是 x n , 2 x_{n,2} xn,2。

结果：
∂ C o s t ∂ w 2 = 1 N ∑ n = 1 N 2 ⋅ x n , 2 ⋅ ( y ^ n − y n ) \frac{\partial Cost}{\partial w_2} = \frac{1}{N} \sum_{n=1}^{N} 2 \cdot x_{n,2} \cdot (\hat{y}_n - y_n) ∂w2∂Cost=N1n=1∑N2⋅xn,2⋅(y^n−yn)

对 b b b 的梯度
∂ C o s t ∂ b = 1 N ∑ n = 1 N 2 ( y ^ n − y n ) ⏟ 外层 ⋅ ∂ z n ∂ b ⏟ 内层 \frac{\partial Cost}{\partial b} = \frac{1}{N} \sum_{n=1}^{N} \underbrace{2(\hat{y}n - y_n)}{\text{外层}} \cdot \underbrace{\frac{\partial z_n}{\partial b}}_{\text{内层}} ∂b∂Cost=N1n=1∑N外层 2(y^n−yn)⋅内层 ∂b∂zn

看 z n z_n zn 的公式： w 1 x n , 1 + w 2 x n , 2 + b − y n w_1 x_{n,1} + w_2 x_{n,2} + b - y_n w1xn,1+w2xn,2+b−yn。
对 b b b 求导，注意 b b b 的系数是 1。
结果：
∂ C o s t ∂ b = 1 N ∑ n = 1 N 2 ⋅ ( y ^ n − y n ) \frac{\partial Cost}{\partial b} = \frac{1}{N} \sum_{n=1}^{N} 2 \cdot (\hat{y}_n - y_n) ∂b∂Cost=N1n=1∑N2⋅(y^n−yn)
(注意：这里没有乘以任何 x x x，因为 b b b 不依附于输入特征)

（3）总结与代码实现的直觉

推导下来你会发现一个极其美妙的规律：

对于 MSE 损失函数：

任意权重的梯度 = 2 × 2 \times 2× (误差) × \times × (该权重对应的输入特征)
偏置的梯度 = 2 × 2 \times 2× (误差) × \times × 1

如果用向量化（Matrix）的写法（这正是PyTorch等框架的做法），公式会变得极其简洁：

设 Input X = [ x 1 , x 2 , 1 ] X = [x_1, x_2, 1] X=[x1,x2,1] (把b看作乘以恒为1的输入)，Weights W = [ w 1 , w 2 , b ] T W = [w_1, w_2, b]^T W=[w1,w2,b]T。

梯度向量为：
∇ W = 2 N X T ( Y ^ − Y ) \nabla W = \frac{2}{N} X^T (\hat{Y} - Y) ∇W=N2XT(Y^−Y)

这就是为什么深度学习框架算梯度那么快，因为不管你有多少个 w w w 和 b b b，本质上都是在一个矩阵乘法里完成的。

求出梯度（或者由梯度组成的向量）之后，就到了最激动人心的**"更新参数"**（Update）环节。这才是"梯度下降"算法真正发挥作用、让模型变聪明的一步。

（4）合成矩阵计算和拆开计算结果相同

对于 W W W来说：

把它们写成矩阵 W W W 一起算，和把它们拆开成 w 1 , w 2 , b w_1, w_2, b w1,w2,b 一个个手算，结果没有任何区别。矩阵运算本质上就是一种**"批量打包"**的算术简写。

设定场景

误差 E = y ^ − y = − 260 E = \hat{y} - y = -260 E=y^−y=−260。
输入 x 1 = 80 , x 2 = 8 x_1 = 80, x_2 = 8 x1=80,x2=8。
偏置项输入 虽然没写，其实默认是 1 1 1。

方法一：单独算（标量法）

这是我们刚才推导的逻辑：

算 w 1 w_1 w1 ： grad w 1 = 2 ⋅ x 1 ⋅ E = 2 × 80 × ( − 260 ) = − 41600 \text{grad}_{w1} = 2 \cdot x_1 \cdot E = 2 \times 80 \times (-260) = \mathbf{-41600} gradw1=2⋅x1⋅E=2×80×(−260)=−41600
算 w 2 w_2 w2 ： grad w 2 = 2 ⋅ x 2 ⋅ E = 2 × 8 × ( − 260 ) = − 4160 \text{grad}_{w2} = 2 \cdot x_2 \cdot E = 2 \times 8 \times (-260) = \mathbf{-4160} gradw2=2⋅x2⋅E=2×8×(−260)=−4160
算 b b b ： grad b = 2 ⋅ 1 ⋅ E = 2 × 1 × ( − 260 ) = − 520 \text{grad}_{b} = 2 \cdot 1 \cdot E = 2 \times 1 \times (-260) = \mathbf{-520} gradb=2⋅1⋅E=2×1×(−260)=−520

结果集： ( − 41600 , − 4160 , − 520 ) (-41600, -4160, -520) (−41600,−4160,−520)

方法二：合起来算（矩阵/向量法）

我们把输入拼成列向量 X = [ 80 , 8 , 1 ] T X = [80, 8, 1]^T X=[80,8,1]T。

我们把梯度看作梯度向量 ∇ W \nabla W ∇W。

公式： ∇ W = 2 ⋅ X ⋅ E \nabla W = 2 \cdot X \cdot E ∇W=2⋅X⋅E

∇ W = 2 × [ 80 8 1 ] × ( − 260 ) \nabla W = 2 \times \begin{bmatrix} 80 \\ 8 \\ 1 \end{bmatrix} \times (-260) ∇W=2× 8081 ×(−260)

标量乘向量，要把标量乘进每一个分量里：

∇ W = [ 2 × 80 × ( − 260 ) 2 × 8 × ( − 260 ) 2 × 1 × ( − 260 ) ] = [ − 41600 − 4160 − 520 ] \nabla W = \begin{bmatrix} 2 \times 80 \times (-260) \\ 2 \times 8 \times (-260) \\ 2 \times 1 \times (-260) \end{bmatrix} = \begin{bmatrix} \mathbf{-41600} \\ \mathbf{-4160} \\ \mathbf{-520} \end{bmatrix} ∇W= 2×80×(−260)2×8×(−260)2×1×(−260) = −41600−4160−520

上述结论

你看，结果每一个数字都分毫不差。

平时做题/理解原理 ：我们喜欢拆开算 ，因为物理意义清晰（ w 1 w_1 w1管面积， w 2 w_2 w2管地段）。
写代码/跑程序 ：我们喜欢合起来算 （矩阵乘法），因为电脑做矩阵乘法比做几千个 for 循环要快这就是几万倍的差距。

对于 ∇ W \nabla W ∇W来说：
∇ W \nabla W ∇W（读作 Gradient of W，即 W 的梯度）单纯就是把那三个单独算出来的数，打包放进了一个括号里。

∇ W = [ ∂ C o s t ∂ w 1 ∂ C o s t ∂ w 2 ∂ C o s t ∂ b ] \nabla W = \begin{bmatrix} \frac{\partial Cost}{\partial w_1} \\ \frac{\partial Cost}{\partial w_2} \\ \frac{\partial Cost}{\partial b} \end{bmatrix} ∇W= ∂w1∂Cost∂w2∂Cost∂b∂Cost

它们不仅结果一样，本质上就是同一个东西 ，只是一个是批发装 （向量写法），一个是零售装（标量写法）。

（5）更新公式（The Update Rule）

求出梯度向量 ∇ W \nabla W ∇W 的计算公式后，我们用下面的公式更新权重矩阵 W W W：

W new = W old − α ⋅ ∇ W W_{\text{new}} = W_{\text{old}} - \alpha \cdot \nabla W Wnew=Wold−α⋅∇W

W old W_{\text{old}} Wold ：现在的参数（比如瞎猜的 w 1 = 2 , w 2 = 3 , b = 7 w_1=2, w_2=3,b=7 w1=2,w2=3,b=7，这个数据就是先瞎找，然后运算）。
− - − (减号) ：梯度的方向是函数值上升最快的方向（上山），我们要找最小值（下山），所以必须反着走。
α \alpha α (alpha) ：学习率 (Learning Rate) 。步长系数，比如 0.01。
- 梯度只告诉你方向和陡峭程度，不告诉你该走多远。 α \alpha α 决定了跨多大一步。
W new W_{\text{new}} Wnew：更新后的参数，用它进行下一轮训练。

5.小批量梯度下降（Mini-Batch GD）

定义：
- 普通梯度下降（Batch GD）：用所有样本计算平均梯度后，更新一次参数（往低谷走一步），然后再拿这次参数计算所有样本的平均梯度，一步步走下去，直到走不动。
- 随机梯度下降（SGD）：每拿一个样本，算一次梯度，立刻更新一次权重，然后下一个样本重复计算，要把所有样本经历好多伦，直到走不下去。
- 小批量梯度下降（Mini-Batch GD）：每次从数据堆里随机抓取一小把样本（比如 32 个），算出这 32 个样本的平均梯度，立刻更新一次权重，然后再抓下一把（新的 32 个）重复计算。把所有样本都抓过一遍后（完成了一个 Epoch），再打乱顺序重新开始抓。
Mini-Batch的核心优势：有效规避鞍点问题
- Batch GD：由于对所有样本梯度取平均（∑梯度=0），虽然地形存在起伏 ，但正负梯度相互抵消，最终计算结果为零梯度，导致模型停滞。
- Mini-Batch：仅采样部分数据 ，无法实现完美梯度抵消（保留方差特性），计算结果为非零梯度，促使模型持续调整，从而避免陷入局部停滞状态

6. 性能对比与最终方案：Mini-Data Batch

特性	梯度下降 (Batch GD)	随机梯度下降 (SGD)
计算方式	所有样本算一次梯度	一个样本算一次梯度
并行计算能力	高（向量化计算）	低（必须串行，无法利用GPU并行）
优化效果	容易卡在鞍点	好（随机性能逃离鞍点）
时间复杂度	低（计算快）	高（循环次数多，慢）
这些方面是怎么从原理解释的

（1）并行计算能力 (Parallel Computation)

简单来说，它指的是将一个大而复杂的计算任务分解成许多小的部分，然后让多个计算单元同时处理这些部分，最终协同完成整个任务的能力。

Batch GD: 无依赖，大家一起算
- 原理：虽然我们要算 10000 个人的梯度，但注意，大家的梯度都是基于同一个 w o l d w_{old} wold 计算的。
- 比喻：老师发卷子考试。全班 50 个人同时做题，互不干扰。
- 硬件：GPU（显卡）有几千个核心，它最喜欢这种任务。它一声令下："核心1算样本1，核心2算样本2... 核心10000算样本10000！" 砰！一瞬间，10000 个梯度全算出来了。 这叫向量化（Vectorization）。
SGD: 强依赖，只能排队算
- 原理：SGD 更新 w w w 是串行的。
  - 第 2 个样本必须等第 1 个样本更新完 w w w 之后，才能基于新的 w w w 开始计算。
  - 第 3 个样本必须等第 2 个...
- 链条： w 0 → w 1 → w 2 → . . . w_0 \to w_1 \to w_2 \to ... w0→w1→w2→...
- 比喻：接力赛跑。第 2 棒必须等第 1 棒跑完交接棒才能跑。你不能让 50 个人同时跑，那样没意义。
- 硬件：GPU 傻眼了。它几千个核心，只有 1 个核心在干活（算第1个样本），其他 9999 个核心都在围观等待 。等算完了，下一个核心再动。这就造成了巨大的算力浪费。

（2）时间复杂度 (Time Complexity)

核心原理：指令开销 vs 数据吞吐

你可能会想：数学上来说，大家不都是把 10000 个数算一遍吗？加法乘法次数一样多啊，为啥 SGD 慢？

这里的"时间复杂度高"，指的不是运算次数，而是计算机的搬运和指令时间（Wall-clock time）。

Batch GD (开大巴车)
- 操作：CPU 给 GPU 下达一条指令："把这 10000 个数据给我乘一下！"
- 消耗：1 次"下令"的时间 + 1 次大规模运算时间。
- 效率：极高。就像用一辆大巴车一次拉走了 10000 人。
SGD (开出租)
- 操作：CPU 需要下达 10000 次指令 。
  - 循环第 1 次："把第 1 个数乘一下！"
  - （等待数据传输回 CPU，更新 w，再传回 GPU...）
  - 循环第 2 次："把第 2 个数乘一下！"
- 消耗：10000 次"下令"的开销 + 数据显存内存来回倒腾的开销。
- 效率：极低。就像用一辆出租车，来回跑了 10000 趟把人运完。虽然人还是那么多人，但时间全浪费在路上了。

（3）工程实践中的关键限制

内存瓶颈（硬件限制）
以ImageNet数据集（1400万张图片）为例：

单张图片(224x224x3)约150KB
全量数据需要约2000GB显存
顶级GPU（如NVIDIA A100）仅80GB显存
实际结果：直接导致内存溢出错误（CUDA Out of Memory）

时间效率问题

假设拥有无限显存：

Batch GD：1小时完成1次全量更新
Mini-Batch(batch_size=100)：同等时间内可完成140,000次更新
实际效果：Mini-Batch通过更频繁的更新能更快收敛

最终方案选择：Mini-Batch

工业界选择Mini-Batch的原因：

平衡了并行计算（支持32-256样本并行）
保留了一定随机性（优于Batch GD）
实现了计算效率与优化效果的最佳平衡

7. 实战举例：10个房价样本的手算训练过程

为了彻底讲透，我们抛开复杂的代码，设定一个具体的微型场景，并从底层数学原理 出发，用 Mini-Batch 梯度下降 手算训练出一个房价预测模型。

（1）准备工作（Data & Model）

1. 数据集 (Data)

假设我们有 10 个样本的"微型数据集"。

x 1 x_1 x1：面积（为了好算，缩小 10 倍，10 代表 100 平）
x 2 x_2 x2：地段（1-5 分）
y y y：真实房价（万元）

样本ID	x 1 x_1 x1 (面积/10)	x 2 x_2 x2 (地段)	y y y (房价)
0	10	2	300
1	8	5	450
2	12	2	350
3	15	3	500
4	6	1	150
5	...	...	...

2. 模型 (Model)

公式： y ^ = w 1 ⋅ x 1 + w 2 ⋅ x 2 + b \hat{y} = w_1 \cdot x_1 + w_2 \cdot x_2 + b y^=w1⋅x1+w2⋅x2+b

3. 初始参数 (Parameters)

我们现在是随机瞎猜的：

w 1 = 0 w_1 = 0 w1=0
w 2 = 0 w_2 = 0 w2=0
b = 0 b = 0 b=0

4. 学习率 (Learning Rate)
α = 0.001 \alpha = 0.001 α=0.001 （步子很小）

（2）训练过程：第一个 Mini-Batch 的诞生

我们设定 Batch Size = 2 。

也就是说，我们这次只抓取 样本0 和 样本1 来训练。

第一步：前向预测 (Forward) ------ 算错得有多离谱？

样本 0 ( x 1 = 10 , x 2 = 2 , y = 300 x_1=10, x_2=2, y=300 x1=10,x2=2,y=300)：
- 预测： y ^ 0 = 0 ⋅ 10 + 0 ⋅ 2 + 0 = 0 \hat{y}_0 = 0 \cdot 10 + 0 \cdot 2 + 0 = 0 y^0=0⋅10+0⋅2+0=0
- 误差（Loss gradient part）： E r r o r 0 = y ^ 0 − y = 0 − 300 = − 300 Error_0 = \hat{y}_0 - y = 0 - 300 = \mathbf{-300} Error0=y^0−y=0−300=−300
  (预测比真实值低了 300)
样本 1 ( x 1 = 8 , x 2 = 5 , y = 450 x_1=8, x_2=5, y=450 x1=8,x2=5,y=450)：
- 预测： y ^ 1 = 0 ⋅ 8 + 0 ⋅ 5 + 0 = 0 \hat{y}_1 = 0 \cdot 8 + 0 \cdot 5 + 0 = 0 y^1=0⋅8+0⋅5+0=0
- 误差： E r r o r 1 = 0 − 450 = − 450 Error_1 = 0 - 450 = \mathbf{-450} Error1=0−450=−450
  (预测比真实值低了 450)

第二步：计算梯度 (Compute Gradient) ------ 谁该背锅？

我们要计算梯度。回忆我们在第4节推导的 MSE 梯度公式：

w 1 w_1 w1 的梯度 = 2 ⋅ x 1 ⋅ E r r o r 2 \cdot x_1 \cdot Error 2⋅x1⋅Error
w 2 w_2 w2 的梯度 = 2 ⋅ x 2 ⋅ E r r o r 2 \cdot x_2 \cdot Error 2⋅x2⋅Error
b b b 的梯度 = 2 ⋅ 1 ⋅ E r r o r 2 \cdot 1 \cdot Error 2⋅1⋅Error

现在我们要算 这一个 Batch（2个样本）的平均梯度。

1. 算 w 1 w_1 w1 的梯度：
- 样本 0 的意见： 2 ⋅ 10 ⋅ ( − 300 ) = − 6000 2 \cdot 10 \cdot (-300) = -6000 2⋅10⋅(−300)=−6000
- 样本 1 的意见： 2 ⋅ 8 ⋅ ( − 450 ) = − 7200 2 \cdot 8 \cdot (-450) = -7200 2⋅8⋅(−450)=−7200
- Batch 平均意见 ： ( − 6000 − 7200 ) / 2 = − 6600 (-6000 - 7200) / 2 = \mathbf{-6600} (−6000−7200)/2=−6600
  (这意味着： w 1 w_1 w1 太小了，要加大！)
2. 算 w 2 w_2 w2 的梯度：
- 样本 0 的意见： 2 ⋅ 2 ⋅ ( − 300 ) = − 1200 2 \cdot 2 \cdot (-300) = -1200 2⋅2⋅(−300)=−1200
- 样本 1 的意见： 2 ⋅ 5 ⋅ ( − 450 ) = − 4500 2 \cdot 5 \cdot (-450) = -4500 2⋅5⋅(−450)=−4500
- Batch 平均意见 ： ( − 1200 − 4500 ) / 2 = − 2850 (-1200 - 4500) / 2 = \mathbf{-2850} (−1200−4500)/2=−2850
  (这意味着： w 2 w_2 w2 也太小了)
3. 算 b b b 的梯度：
- 样本 0 的意见： 2 ⋅ 1 ⋅ ( − 300 ) = − 600 2 \cdot 1 \cdot (-300) = -600 2⋅1⋅(−300)=−600
- 样本 1 的意见： 2 ⋅ 1 ⋅ ( − 450 ) = − 900 2 \cdot 1 \cdot (-450) = -900 2⋅1⋅(−450)=−900
- Batch 平均意见 ： ( − 600 − 900 ) / 2 = − 750 (-600 - 900) / 2 = \mathbf{-750} (−600−900)/2=−750

第三步：参数更新 (Update) ------ 改过自新

拿着刚才算出来的平均梯度，修改我们的参数。
w n e w = w o l d − α ⋅ G r a d i e n t w_{new} = w_{old} - \alpha \cdot Gradient wnew=wold−α⋅Gradient

w 1 w_1 w1 更新 ：
0 − 0.001 × ( − 6600 ) = 0 + 6.6 = 6.6 0 - 0.001 \times (-6600) = 0 + 6.6 = \mathbf{6.6} 0−0.001×(−6600)=0+6.6=6.6
w 2 w_2 w2 更新 ：
0 − 0.001 × ( − 2850 ) = 0 + 2.85 = 2.85 0 - 0.001 \times (-2850) = 0 + 2.85 = \mathbf{2.85} 0−0.001×(−2850)=0+2.85=2.85
b b b 更新 ：
0 − 0.001 × ( − 750 ) = 0 + 0.75 = 0.75 0 - 0.001 \times (-750) = 0 + 0.75 = \mathbf{0.75} 0−0.001×(−750)=0+0.75=0.75

（3）见证奇迹：完整跑完第二个 Mini-Batch

第一轮更新后，参数变成了：
w 1 = 6.6 , w 2 = 2.85 , b = 0.75 w_1 = 6.6, \quad w_2 = 2.85, \quad b = 0.75 w1=6.6,w2=2.85,b=0.75

现在的模型已经不是当初那个"一无所知"的傻瓜了，我们立刻用这套新参数 来训练 Batch 2（包含样本 2 和样本 3）。

第一步：前向预测 (Forward) ------ 看看进步了多少？

样本 2 ( x 1 = 12 , x 2 = 2 , y = 350 x_1=12, x_2=2, y=350 x1=12,x2=2,y=350)：
- 预测： y ^ 2 = 6.6 ⋅ 12 + 2.85 ⋅ 2 + 0.75 = 79.2 + 5.7 + 0.75 = 85.65 \hat{y}_2 = 6.6 \cdot 12 + 2.85 \cdot 2 + 0.75 = 79.2 + 5.7 + 0.75 = \mathbf{85.65} y^2=6.6⋅12+2.85⋅2+0.75=79.2+5.7+0.75=85.65
  (之前的预测是 0，现在已经是 85.65 了！虽然离 350 还有差距，但进步巨大。)
- 误差： E r r o r 2 = 85.65 − 350 = − 264.35 Error_2 = 85.65 - 350 = \mathbf{-264.35} Error2=85.65−350=−264.35
样本 3 ( x 1 = 15 , x 2 = 3 , y = 500 x_1=15, x_2=3, y=500 x1=15,x2=3,y=500)：
- 预测： y ^ 3 = 6.6 ⋅ 15 + 2.85 ⋅ 3 + 0.75 = 99 + 8.55 + 0.75 = 108.3 \hat{y}_3 = 6.6 \cdot 15 + 2.85 \cdot 3 + 0.75 = 99 + 8.55 + 0.75 = \mathbf{108.3} y^3=6.6⋅15+2.85⋅3+0.75=99+8.55+0.75=108.3
- 误差： E r r o r 3 = 108.3 − 500 = − 391.7 Error_3 = 108.3 - 500 = \mathbf{-391.7} Error3=108.3−500=−391.7

第二步：计算梯度 (Compute Gradient) ------ 继续修正

1. 算 w 1 w_1 w1 的梯度：
- 样本 2： 2 ⋅ 12 ⋅ ( − 264.35 ) = − 6344.4 2 \cdot 12 \cdot (-264.35) = -6344.4 2⋅12⋅(−264.35)=−6344.4
- 样本 3： 2 ⋅ 15 ⋅ ( − 391.7 ) = − 11751 2 \cdot 15 \cdot (-391.7) = -11751 2⋅15⋅(−391.7)=−11751
- Batch 平均 ： ( − 6344.4 − 11751 ) / 2 ≈ − 9047.7 (-6344.4 - 11751) / 2 \approx \mathbf{-9047.7} (−6344.4−11751)/2≈−9047.7
2. 算 w 2 w_2 w2 的梯度：
- 样本 2： 2 ⋅ 2 ⋅ ( − 264.35 ) = − 1057.4 2 \cdot 2 \cdot (-264.35) = -1057.4 2⋅2⋅(−264.35)=−1057.4
- 样本 3： 2 ⋅ 3 ⋅ ( − 391.7 ) = − 2350.2 2 \cdot 3 \cdot (-391.7) = -2350.2 2⋅3⋅(−391.7)=−2350.2
- Batch 平均 ： ( − 1057.4 − 2350.2 ) / 2 ≈ − 1703.8 (-1057.4 - 2350.2) / 2 \approx \mathbf{-1703.8} (−1057.4−2350.2)/2≈−1703.8
3. 算 b b b 的梯度：
- 样本 2： 2 ⋅ 1 ⋅ ( − 264.35 ) = − 528.7 2 \cdot 1 \cdot (-264.35) = -528.7 2⋅1⋅(−264.35)=−528.7
- 样本 3： 2 ⋅ 1 ⋅ ( − 391.7 ) = − 783.4 2 \cdot 1 \cdot (-391.7) = -783.4 2⋅1⋅(−391.7)=−783.4
- Batch 平均 ： ( − 528.7 − 783.4 ) / 2 ≈ − 656.05 (-528.7 - 783.4) / 2 \approx \mathbf{-656.05} (−528.7−783.4)/2≈−656.05

第三步：参数再次更新 (Update)

w 1 w_1 w1 更新 ： 6.6 − 0.001 × ( − 9047.7 ) = 6.6 + 9.05 = 15.65 6.6 - 0.001 \times (-9047.7) = 6.6 + 9.05 = \mathbf{15.65} 6.6−0.001×(−9047.7)=6.6+9.05=15.65
w 2 w_2 w2 更新 ： 2.85 − 0.001 × ( − 1703.8 ) = 2.85 + 1.70 = 4.55 2.85 - 0.001 \times (-1703.8) = 2.85 + 1.70 = \mathbf{4.55} 2.85−0.001×(−1703.8)=2.85+1.70=4.55
b b b 更新 ： 0.75 − 0.001 × ( − 656.05 ) = 0.75 + 0.66 = 1.41 0.75 - 0.001 \times (-656.05) = 0.75 + 0.66 = \mathbf{1.41} 0.75−0.001×(−656.05)=0.75+0.66=1.41

(结论) ：仅仅过了两个 Batch（也就是看了4个房子）， w 1 w_1 w1 就从 0 涨到了 15.65（越来越接近真实的权重了）。这就是 Mini-Batch 的威力：步频快，迭代快。

（4）底层逻辑总结

这就是 Mini-Batch 的精髓：

取样：只抓 2 个进来（样本 0, 1）。
问责：算这 2 个人的账，发现 w 1 , w 2 , b w_1,w_2,b w1,w2,b 亏欠。
通过：立刻补偿 w 1 , w 2 , b w_1,w_2,b w1,w2,b。
下一轮 ：再面对后续样本时，我已经是一个更好、更强的模型了。

（5）终局：什么时候才算"训练完成"？

你可能会问：我们要这样算到什么时候头？是一直算到天荒地老吗？

通常有三个标志告诉我们"可以收工了"：

Loss 足够小（达到目标） ：

比如我们发现预测房价和真实房价的误差只差 100 块钱了，满足了业务需求，就可以停止。
梯度趋近于 0（到了谷底/收敛） ：

当你发现算出来的梯度非常小，乘上学习率后， w w w 的修改量微乎其微（比如从 15.65 15.65 15.65 变成 15.65001 15.65001 15.65001）。这就说明我们已经站在了最低点（或者鞍点/局部最优），再怎么走也走不动了，这时候就可以停止。
达到预设轮数（Epoch） ：

在实际代码中，我们通常会规定："把这 10 个数据反复看 100 遍（100 Epochs）"。跑完就强制停止。

这里需要区分两个概念：
- Epoch (轮)：把所有训练数据（这里是10个样本）完整过一遍，叫 1 个 Epoch。
- Iteration / Step (步)：更新一次参数（跑一个 Mini-Batch），叫 1 个 Step。
- 换算关系：如果我们有 10 个样本，Batch Size = 2。那么 1 个 Epoch = 5 个 Iteration。也就是每过完一轮，参数已经更新了 5 次。

在刚才的例子中 ：

我们现在的 w 1 = 15.65 w_1=15.65 w1=15.65，假设真实的最优解是 w 1 = 30 w_1=30 w1=30。那说明现在的误差还很大，梯度也很大。我们需要继续跑 Batch 3, Batch 4... 跑完一轮后再从头开始跑 Batch 1... 直到 w 1 w_1 w1 稳定在 30 附近，怎么算梯度都接近 0 为止。

8. 代码复现（对应上述手算过程）

这里我们用最纯粹的 Python 代码把刚才的手算过程跑一遍，你会发现代码就是数学公式的直接翻译。为了方便理解，这里不使用 PyTorch 库，而是直接写公式。

python 复制代码

# ===========================
# 1. 准备数据和初始参数
# ===========================

# 样本数据 (只列出前4个用于演示)
# x1: 面积, x2: 地段, y: 房价
data = [
    {'x1': 10, 'x2': 2, 'y': 300},  # Sample 0
    {'x1': 8,  'x2': 5, 'y': 450},  # Sample 1
    {'x1': 12, 'x2': 2, 'y': 350},  # Sample 2
    {'x1': 15, 'x2': 3, 'y': 500},  # Sample 3
]

# 初始参数 (Blind Guess)
w1 = 0
w2 = 0
b = 0

# 超参数
alpha = 0.001       # 学习率
batch_size = 2      # 一个 Batch 有 2 个样本

print(f"【初始状态】 w1={w1}, w2={w2}, b={b}")
print("-" * 50)

# ===========================
# 2. 开始训练 (模拟 2 个 Batch)
# ===========================

# 把数据切分成 Batches
# range(0, 4, 2) 会产生: 0, 2
# 意味着第一轮取 data[0:2], 第二轮取 data[2:4]
for i in range(0, len(data), batch_size):
    
    batch_data = data[i : i+batch_size] 
    print(f"\n>>> 正在处理 Batch {i//batch_size + 1} (样本 {i} 到 {i+batch_size-1})")
    
    # 初始化这个 Batch 的总梯度
    grad_w1_sum = 0
    grad_w2_sum = 0
    grad_b_sum = 0
    
    # --- Step 1 & 2: 对 Batch 里的每个样本算误差和梯度 ---
    for sample in batch_data:
        x1 = sample['x1']
        x2 = sample['x2']
        y = sample['y']
        
        # 1. Forward (前向预测)
        y_pred = w1 * x1 + w2 * x2 + b
        
        # 2. Error (算误差)
        error = y_pred - y
        print(f"   [样本] 真实值={y}, 预测值={y_pred:.2f}, 误差={error:.2f}")
        
        # 3. Accumulate Gradient (累计梯度)
        # 公式: grad = 2 * error * x
        grad_w1_sum += 2 * error * x1
        grad_w2_sum += 2 * error * x2
        grad_b_sum += 2 * error * 1
        
    # --- 计算平均梯度 ---
    avg_grad_w1 = grad_w1_sum / batch_size
    avg_grad_w2 = grad_w2_sum / batch_size
    avg_grad_b  = grad_b_sum  / batch_size
    
    print(f"   [梯度] w1平均梯度: {avg_grad_w1:.2f}")
    
    # --- Step 3: Update Parameters (更新参数) ---
    w1 = w1 - alpha * avg_grad_w1
    w2 = w2 - alpha * avg_grad_w2
    b  = b  - alpha * avg_grad_b
    
    print(f"   [更新后参数] w1={w1:.4f}, w2={w2:.4f}, b={b:.4f}")

print("-" * 50)
print("训练演示结束。")

代码输出结果对照：

如果你运行这段代码，你会看到控制台打印出和我们手算一模一样的数字：

Batch 1 输出：

w1平均梯度: -6600.00
更新后参数: w1=6.6000

Batch 2 输出：

w1平均梯度: -9047.70
更新后参数: w1=15.6477 (也就是我们手算的 15.65)

9. 梯度下降的本质

梯度下降的本质是：

1.初始状态 ：先随机选定一组参数（瞎猜）。
2.找差距（Forward） ：算出模型预测值与真实值的差异，即损失函数（Loss）。
3.找方向（Backward） ：关键点来了------虽然表面上我们是用 Loss 分别计算每个参数的偏导，但参数之间其实是紧密耦合的。它们共同决定了 Loss，因此是在 Loss 这个唯一的'总指挥'约束下，互相配合、协同调整（牵一发而动全身）。
4.进化（Update） ：修正参数后，进入下一个样本（或 Batch）。
5.循环：通过大量样本和多轮次（Epochs）的反复磨合，直到偏导趋近于 0，模型收敛。"

10. 深度答疑：直击灵魂的三个追问

读者在学习梯度下降时，常会有以下三个极具深度的疑问。这些问题直指算法的本质缺陷。

Q1：梯度下降容易陷入局部最优吗？鞍点又是怎么回事？（高维空间的真相）

这是一个非常经典且容易被误解的问题。真相取决于我们所处的维度：

低维空间（如 1维、2维） ：
局部最优（Local Minima）确实是主要杀手。任何一个像波浪一样的函数，都有很多小坑。小球滚进去就出不来了，去不了最深的大海沟（全局最低）。
高维空间（深度学习场景 - 数百万参数） ：
局部最优其实很难遇到，真正的杀手是"鞍点（Saddle Point）"。
- 为什么难遇到局部最优？（概率论）
  
  要形成一个真正的局部最优，要求这个点在所有维度上（比如 100 万个维度）曲线都要向上弯曲（全是谷底）。这就像你扔 100 万次硬币，要求每一次全是正面朝上，概率微乎其微。
- 鞍点是如何产生的？（你的直觉是对的）
  
  你之前疑惑："只求出二维（单个参数）的局部小值，没考虑高维啊！" 这正是鞍点的成因。
  
  更常见的情况是：100万个维度中，50万个方向曲线向上弯（像碗底，导数=0），另外50万个方向曲线向下弯（像山峰，导数=0）。这就像你扔 100 万次硬币，要求5万次是向上的，50万次是向下的，概论要大于全是向上的。
  - 结果：综合来看梯度向量 ∇ W = 0 \nabla W = 0 ∇W=0。算法以为到了终点不动了，但其实这里既不是山峰也不是山谷，而是马鞍形状的鞍点。
- 结论：在深度学习中，我们大多数时间是在和鞍点以及**平原（Plateau）**做斗争，而不是局部最优。

Q2：既然这么多坑，这些都不是问题吗？

是问题！非常大的问题！

正因为如此，原始的梯度下降（Vanilla Gradient Descent）在工业界几乎没人用。为了解决这些问题，还是那句话：

对抗鞍点 ：引入随机性（SGD / Mini-Batch），把小球从鞍点震下去。
对抗停滞 ：引入动量（Momentum），给小球一个惯性，冲过平坦地带（后续课程会讲）。
对抗学习率敏感 ：引入自适应学习率算法（如 Adam），自动调整步幅（后续课程会讲）。

Q3：每个参数都到了"低点"（偏导为0），怎么能证明合起来就是全维度的最低点？

这个问题非常硬核，甚至涉及到了凸优化的证明！

修正一个概念 ：

梯度为 0 意味着在当前位置，无论往哪个参数方向走，函数值暂时都不会变化（切线是平的）。但这并不代表已经到了最低点（可能是波峰，也可能是平台）。
数学上的"二阶验证"（海森矩阵） ：

要证明是"真·最低点"，除了看一阶导数（梯度）是否为 0，还要看二阶导数（曲率）。
- 我们把所有二阶导数排成一个矩阵，叫海森矩阵（Hessian Matrix）。
- 只有当这个矩阵是"正定 "的（简单说就是所有特征值都大于0），才意味着所有维度的曲线都在向上弯曲（像一个碗），这才能证明是局部极小值。
线性回归的特殊性（完美的大碗） ：

在本讲的线性回归 问题中，我们的运气非常好。MSE 损失函数是一个凸函数（Convex Function）。
- 它的形状就是一个完美的、光滑的大碗（只有一个坑）。
- 数学上可以证明：凸函数的局部最小值，就是全局最小值。
- 所以，只要我们在 MSE 上找到了梯度为 0 的点，它100% 确定就是全维度的最低点。
深度网络的现实（在此只求够用） ：

但在未来的深度神经网络 中，函数起起伏伏，我们无法证明现在处于全局最低点。
- 真相是 ：我们大概率确实没跑到全局最低点（Global Minima）。
- 但是：只要这个局部坑（Local Minima）或者平原足够低，误差（Loss）能满足业务需求（比如房价预测误差在100元以内），我们就没必要非去寻找那个传说中的"绝对最低点"。工程上讲究"够用就好"。

Q4：怎么理解"虽然表面上我们是用 Loss 分别计算每个参数的偏导，但参数之间其实是紧密耦合的"

举一个最直观的**"跷跷板"或者"做菜"**的例子，让你秒懂"参数耦合"。

例子：神经网络就像炒一盘菜 ( 预测结果 = 味道 )

假设我们的模型（神经网络）任务是做一道"西红柿炒鸡蛋"，目标是**味道评分（Loss）**最高。

我们的"参数"有两个：

w 1 w_1 w1（盐的克数）
w 2 w_2 w2（糖的克数）

现在我们来看为什么它们是耦合的：

1. 如果它们"各玩各的"（互相不理）

w 1 w_1 w1 的逻辑 ：我觉得现在的菜有点淡，根据偏导数，我要加 5克盐。
w 2 w_2 w2 的逻辑 ：我觉得现在的菜有点酸，根据偏导数，我要加 10克糖。
结果：你俩各加各的，最后可能炒出来一盘"又咸又甜"的怪味菜，大家都吃不下去（Loss 很高）。

2. 它们"互相耦合"的真相

在 Loss 函数（味道）面前， w 1 w_1 w1 和 w 2 w_2 w2 是互相制约的：

场景A：你本来没放糖 ( w 2 = 0 w_2=0 w2=0)
- 这时候如果你放了 3克盐 ( w 1 = 3 w_1=3 w1=3)，可能咸淡正好，味道完美（Loss低）。
- 结论：在 w 2 w_2 w2 很小的时候， w 1 w_1 w1 大概 3 就够了。
场景B：你手抖放了很多糖 ( w 2 = 20 w_2=20 w2=20)
- 为了压住这么甜的味道，你可能需要放 10克盐 ( w 1 = 10 w_1=10 w1=10) 才能平衡口感。
- 结论：当 w 2 w_2 w2 变大了， w 1 w_1 w1 的"最佳值"也被迫必须要变大！

核心结论

你不能只问"盐多少克最好？"，你必须问"在糖放了这么多克的情况下，盐放多少克最好？"

这就是耦合：

一个参数的梯度（该怎么调），完全取决于 另一个参数当前的值。 w 1 w_1 w1 的命运不仅仅掌握在自己手里，还掌握在 w 2 w_2 w2 手里。在深度神经网络中，几百万个参数就像几百万种调料，它们必须同时找到一种极其微妙的平衡，才能炒出那盘完美的菜。

11.总结课程的逻辑链

穷举和分治（分块不容易找到最低值）不行 → \rightarrow → 用梯度下降 → \rightarrow → 遇到鞍点卡住 → \rightarrow → 改用随机梯度下降（引入噪声破局） → \rightarrow → 随机梯度太慢（无法并行） → \rightarrow → 最终选择 Mini-Batch GD（速度与效果的平衡）。