ms-Mamba: Multi-scale Mamba for Time-Series Forecasting
关于Transformer模型在时间预测任务中的局限性
1、注意力机制局限性:难以捕捉关键的时间依赖关系
虽然Transformer模型最初是为NLP设计的,并因其自注意力机制在捕获长程依赖关系方面的出色表现而被应用于时间序列预测任务,但在处理时间序列数据时,其基于内容的注意力机制暴露了关键缺陷:
- 难以检测关键的时间依赖关系 :Transformer的注意力机制是基于内容(content-based)的 ,这意味着它主要根据序列中不同元素之间的相似性来建立连接,而不是明确地建模时间结构。
- 依赖关系随时间减弱的问题 :这种基于内容的机制在处理那些依赖关系随时间逐渐减弱(vanishing correlations over extended horizons)的序列时,表现不佳。
- 强季节性模式问题 :当时间序列数据中**存在强大的季节性模式**(strong seasonal patterns)时,Transformer的标准注意力机制也难以有效检测或处理这些模式
2、计算复杂度,二次方复杂度限制了长序列处理能力
Transformer模型的另一个主要限制是其自注意力机制的二次方复杂度
- 复杂度与序列长度的关系 :对于长度为 L 的输入序列,标准的自注意力机制 的计算成本和内存使用量是 O ( L 2 L^2 L2),即与序列长度的平方成正比。
- 对长序列的影响 :在时间序列预测中,处理长输入序列(long input sequences)以捕获长期模式是很常见的需求,但二次方复杂度极大地增加了计算成本和内存使用,成为模型应用的一个限制因素
时间序列预测线性模型发挥的作用:
1、线性模型的优势:简洁与效率
线性模型(通常使用多层感知机,MLPs)的优点:它们架构更简单、速度更快,相比于基于Transformer的模型具有更高的效率
2、线性模型的局限性:缺乏复杂的建模能力
为了追求速度和简洁性,线性模型牺牲了关键的建模能力:
- 难以处理非线性依赖关系 :这些模型通常难以处理复杂的非线性依赖关系(non-linear dependencies)。
- 不适用于复杂模式:在涉及**高度波动(highly volatile)或非平稳(non-stationary)**模式的场景中,线性模型的性能往往不佳。
- 难以捕捉全局依赖关系:与Transformer模型相比,线性架构在**捕捉全局依赖关系(global dependencies)**方面效率较低
3、局限性带来的计算成本悖论
线性模型缺乏全局依赖关系捕捉能力的后果,反而抵消了其"更快"的优势:
- 对长输入序列的需求 :由于线性架构不能像Transformer那样高效地捕捉全局信息,为了达到可比较的预测性能,它需要更长的输入序列(longer input sequences)。
- 计算成本增加 :对更长输入序列的需求,即使模型本身是线性的,也会增加整体的计算成本
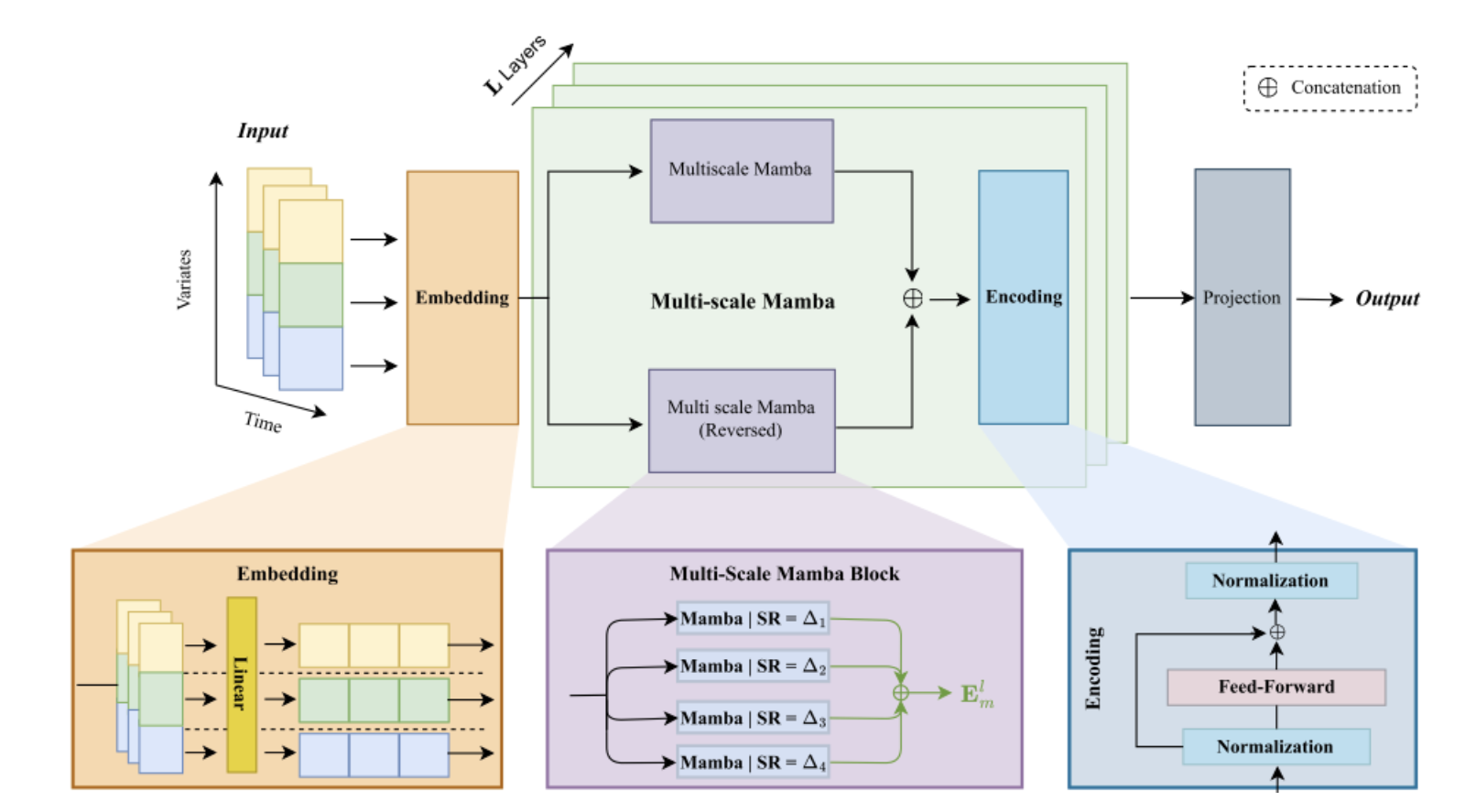
多尺度 Mamba 层(Multi-scale Mamba Layer)的结构
传统的SSMs、Mamba 及其变体(如 S-Mamba)在处理时间序列数据时,通常只使用一个可学习的采样率 Δ。然而,时间序列数据本质上包含多个时间尺度的信号和模式。
ms-Mamba 的目标: ms-Mamba 旨在解决这一不足,通过在不同的采样率 下处理输入,从而更好地捕捉和利用时间序列数据的多尺度特性。
实现机制: ms-Mamba 是通过**组合多个 Mamba 模块(Mamba blocks)**来实现的,每个模块都配置了不同的采样率 Δ i Δ_i Δi
对于第 l 层的输出嵌入 E l E^l El,ms-Mamba 层将其分解并进行并行处理:
E m l = A v g ( M a m b a ( E l ; Δ 1 ) , ... , M a m b a ( E l ; Δ n ) ) E^l_m=Avg(Mamba(E_l;Δ_1),...,Mamba(E_l;Δ_n)) Eml=Avg(Mamba(El;Δ1),...,Mamba(El;Δn))
这意味着:
- 输入嵌入 E l E^l El 被送入 n 个并行的 Mamba 模块。
- 每个 Mamba 模块使用一个特定的采样率 Δ i Δ_i Δi 进行处理。
- 最终的输出 E m l E^l_m Eml 是这 n 个并行处理结果的平均值(Avg)。
- 获取不同采样率 Δ i Δ_i Δi 的三种策略
为了得到用于并行 Mamba 模块的不同采样率 Δ i Δ_i Δi ,ms-Mamba 探索了三种不同的策略:
策略 1:固定时间尺度(Fixed temporal scales)
在这种方法中,只有基础采样率 Δ1 是可学习的(类似于原始 Mamba 模型)。而其他的采样率 Δ2,Δ3,...,Δn 则通过 Δ1 乘以固定的超参数(hyper-parameters) α i α_i αi 来获得:
Δ i = α i × Δ 1 , i ∈ { 2 , ... , n } Δ_i=α_i×Δ_1,i∈\{2,...,n\} Δi=αi×Δ1,i∈{2,...,n}
特点: α i α_i αi 是超参数。通过消融实验发现,系数 α=(1,2,4,8) 在不同数据集上表现最佳。这种方法引入了额外的需要调优的超参数,是一个限制。
策略 2:可学习时间尺度(Learnable temporal scales)
在这种方法中,所有的采样率 Δ i Δ_i Δi 都被定义为独立的可学习变量,就像原始 Mamba 模型中的 Δ 一样。
特点: 这种方法通常能提供略优于最佳固定尺度版本的结果,并且避免了对 α i α_i αi 超参数的调优,因此可能是更优选的选项。
策略 3:动态时间尺度(Dynamic temporal scales)
这是最灵活的方法,其中所有的采样率 Δ i Δ_i Δi 都是通过一个**多层感知机(MLP)**根据当前的输入嵌入 E l E_l El 动态估计出来的:
Δ i = M L P ( F l a t t e n ( E l ) ) Δ_i=MLP(Flatten(E_l)) Δi=MLP(Flatten(El))
实现细节:
- Flatten(·) :首先将输入张量 E l E_l El(维度为 L × D e L×D_e L×De,其中 L 是序列长度, D e D_e De 是嵌入维度)展平为一个维度为 L ∗ D e L*D_e L∗De 的向量。
- MLP(·) :该 MLP 由两个线性层组成,中间夹着一个 ReLU 激活函数: M L P ( x ) = W 2 ∗ m a x ( 0 , W 1 x + b 1 ) + b 2 MLP(x)=W_2*max(0,W_1x+b_1)+b_2 MLP(x)=W2∗max(0,W1x+b1)+b2。
- MLP 的作用是将展平后的输入映射到 n 个不同的采样率 Δi。