yolo26 阅读笔记

创新点：

• 1. 移除分布焦点损失(DFL)
• 2. nms free
• 3. C3k2模块更新
• 4. ProgLoss（渐进损失平衡） 与 STAL（小目标感知标签分配）
• 5. MuSGD

相关技术

解耦检测头

早期yolo（v1/v2/v3/v4/v5）使用的是耦合检测头：

• 同一个卷积层输出类别概率与边框回归参数。
• 分类与回归共享特征，并用同一个 Head 网络处理输出。
• 这种设计简单但无法最好地兼顾分类与几何回归任务需求。
  Revisiting the Sibling Head in Object Detector（CVPR 2020）指出传统 sibling head（耦合在同一个 Head 上预测分类和定位）存在 空间冲突（spatial misalignment） 问题，并引入 task-aware spatial disentanglement（TSD）来实质上 decouple 两个任务的特征：该思想从目标检测 Head 的空间特性角度提出了解耦需要：分类更关注语义中心特征，而定位更关注边界或几何信息。

YOLO系列中，YOLOX最早明确提出并应用 Decoupled Head：在预测输出端将分类分支和边框回归分支分离出来（如下图）。

作者指出：解耦 Head 有助于提升精度和收敛速度，并在 YOLOv3 基线的实验中显著提高了性能。

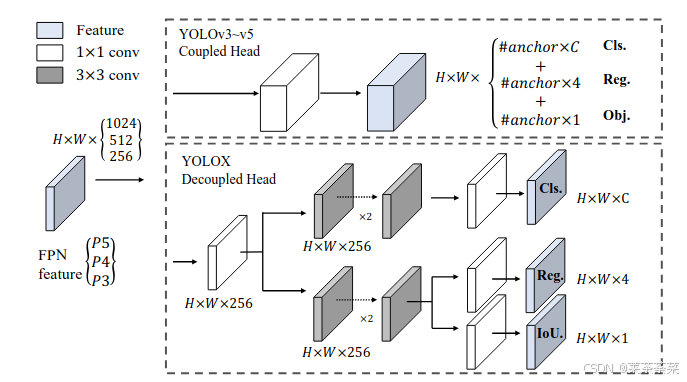
无锚框预测

YOLO系列中YOLOX率先使用anchor_free。加之上面提到的解耦head，anchor_free 也会更加稳定。之前的v2-v5中，回归任务回归的都是anchor → GT box 的偏移量

之前有锚框回归过程：

网络输出：tx, ty, tw, th
bx=(sigmoid(tx)+cx)∗strideb_x = (sigmoid(t_x) + c_x) * stridebx=(sigmoid(tx)+cx)∗stride
by=(sigmoid(ty)+cy)∗strideb_y = (sigmoid(t_y) + c_y) * strideby=(sigmoid(ty)+cy)∗stride
bw=anchorw∗exp(tw)b_w = anchor_w * exp(t_w)bw=anchorw∗exp(tw)
bh=anchorh∗exp(th)b_h = anchor_h * exp(t_h)bh=anchorh∗exp(th)

有没有小伙伴和我一样 对于box的xy的回归很容易回想起来，w，h却总是忘记为什么求指数。我们按当年设计者的思路一步步复原为什么这么算。

首先为什么设计时要用：tw=log(bw/anchorw)t_w = log(b_w/anchor_w)tw=log(bw/anchorw)，而不是bw=anchorw+twb_w = anchor_w + t_wbw=anchorw+tw 或者 bw=anchorw∗twb_w = anchor_w * t_wbw=anchorw∗tw？

第一：预测框的宽高必须为正，如果bw=anchorw+twb_w = anchor_w + t_wbw=anchorw+tw，tw<−anchorwt_w < -anchor_wtw<−anchorw, bwb_wbw就小于零了，而bw=anchorw∗exp(tw)b_w = anchor_w * exp(t_w)bw=anchorw∗exp(tw)恒为正。

第二：希望学到的是相对尺度变化，梯度随尺度自适应，多尺度特征下分布稳定
L=∣tpredw−log(GTw/anchorw)∣L = |t^w_{pred} - log(GT_w / anchor_w)|L=∣tpredw−log(GTw/anchorw)∣

同一类别在不同尺度层（P3 / P4 / P5）上，回归分布一致

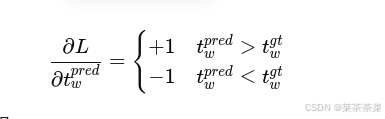
回归目标近似服从 0 均值分布，非常适合 L1 / Smooth-L1

第三：梯度要好训

加法模型bw=anchorw+tw；∂bw/∂tw=1b_w = anchor_w + t_w ；∂b_w/∂t_w = 1bw=anchorw+tw；∂bw/∂tw=1，大框 / 小框回归梯度相同 → 不稳定

乘法模型bw=anchorw∗tw；twb_w = anchor_w * t_w ；t_wbw=anchorw∗tw；tw 必须 > 0（又要约束），小于 1 的尺度压缩非常难学

无锚框的回归过程：
l=x−xleftl = x - x_{left}l=x−xleft
r=xright−xr = x_{right} - xr=xright−x

这些量：天然 ≥ 0，本身就是"几何距离"

DFL（分布焦点损失）

DFL是一种用离散分布回归连续距离的回归建模方式，以YOLOX为例，回归的是l, t, r, b （像素距离），loss为IoU / GIoU / L1。

核心思想

把一个连续距离，拆成「若干离散 bin 的概率分布」

例如：

最大回归距离：reg_max = 16，不再预测一个l ，而是预测一个长度为 17 的向量：

P(l = 0), P(l = 1), ..., P(l = 16)

lbtr各自计算期望（Expectation），例如对l

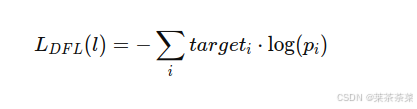
然后对ltrb求和

优点

• 传统的回归是直接预测一个实数
• 梯度高度依赖预测误差
• 对边界不确定性建模能力弱

DFL 和 Anchor-free 天然契合

• ltrb 天然 ≥ 0
• 有合理上界
• 距离有"离散感"（像素）

DFL 带来的好处

• 回归更稳定（尤其 early stage）
• 对模糊边界更鲁棒
• 和 IoU loss 互补
• AP 有稳定增益（尤其 AP75）

AP75 是什么？ IoU ≥ 0.75 的平均精度，AP 用的是：Precision / Recall

YOLO-26 的回归目标已经不是"像素精度优先"，YOLO-26 的核心设计目标是：NMS-free + 匈牙利匹配 + 全局最优分配。

在这个体系里：一个 GT 通常只匹配 1 个预测，不再需要大量候选框"拼精度"

DFL 的优势："在大量候选中，把边界磨得更准"

而 YOLO-26："我要的是全局最优的一对一匹配"，优化目标不同了

匈牙利匹配使用的 cost 通常是：cost = cls_cost + box_cost (L1 / IoU)

而 DFL：回归的是分布，loss 是分类型交叉熵，与 box L1 / IoU 是"异构目标"

nms free技术

在训练阶段就实现一对一预测，而实现不用nms的技术

传统yolo步骤

输出很多候选框 → 通过规则筛选 → NMS 去重 → 最终预测框

每个 anchor / 每个 grid cell 输出：

输出	说明
bbox = (x, y, w, h)	回归框
obj_conf	是否包含物体（objectness score）
class_conf[C]	类别概率

通常在推理阶段计算：
score=objconf×classconfscore=obj_{conf}×class_{conf}score=objconf×classconf

首先:进行置信度筛选 ：score < confthreshconf_{thresh}confthresh → 丢弃, 只保留高置信度候选框, 筛掉绝大部分背景框。

接着：NMS （同类别去重）

按 score 排序；对每个类别单独取最高 score 框；删除与它 IoU > nms_thresh 的其余框；迭代直到没有候选框

YOLO26的处理步骤：

每个 grid cell / anchor-free 位置输出：

输出	说明
ltrb 或 (x, y, w, h)	回归框
class_conf[C]	类别概率

候选点筛选

只考虑 GT 中心区域内的预测点，其他位置全部负样本

计算 cost / alignment metric

SimOTA：
cost=clsloss+λ⋅IoUlosscost=cls_{loss}+λ⋅IoU_{loss}cost=clsloss+λ⋅IoUloss

Task-Aligned：

align=(pcls)α⋅(IoU)β(p_{cls})^α⋅(IoU)^β(pcls)α⋅(IoU)β

Task-Aligned 直接考虑最终得分与框质量对齐

选 top-K（通常 1-3 个）

GT 只分配给最优预测,其余候选点为负样本,这一步让训练天然"一物一框"，减少重复预测

推理时

score = class_{conf} × IoU_{pred} ,丢掉低置信框, 每个位置只输出一个框，每张图 Top-K 限制输出数

无需 NMS

因为训练时已经让每个 GT 只有一个高质量框

名称	核心改进	每步动作
SimOTA	动态选正样本数 K（每个 GT 可以有 1~K 个正样本）	1. 候选预测点（中心区域） 2. 计算 cost = clsloss+IoUlosscls_{loss} + IoU_{loss}clsloss+IoUloss 3. top-K cost 最低的点分配给 GT
Task-Aligned	对齐预测得分和正样本选择（NMS-Free 必需）	1. 候选预测点 2. 计算 alignment = (clsconf)α∗IoUβ(cls_{conf})^α * IoU^β(clsconf)α∗IoUβ 3. top-K alignment 最大的点分配给 GT 4. 其余负样本

PSA模块

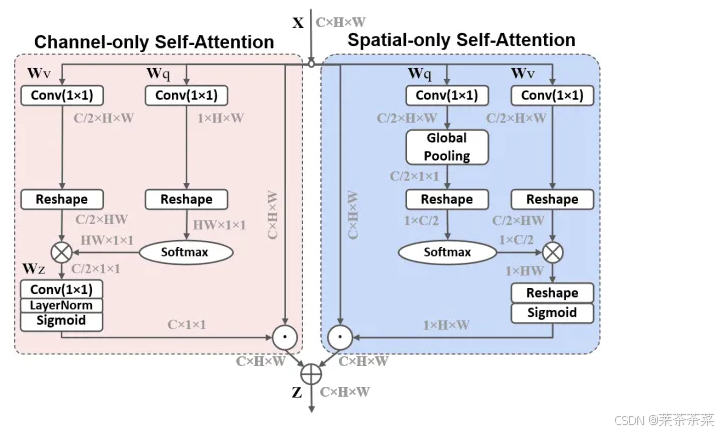
C3k2模块

yolov11:

Backbone

├─ Conv

├─ C2f / C3

├─ PSA ← 插在 stage 末尾（较粗粒度）

yolo26PSA 被下沉到 C3k2 Block 内部，变成了"结构性分支"

新C3K2

Input

├─ Bottleneck 分支（局部、几何）

├─ PSA 分支 （全局、注意力） ← 新加

└─ Concat + Conv

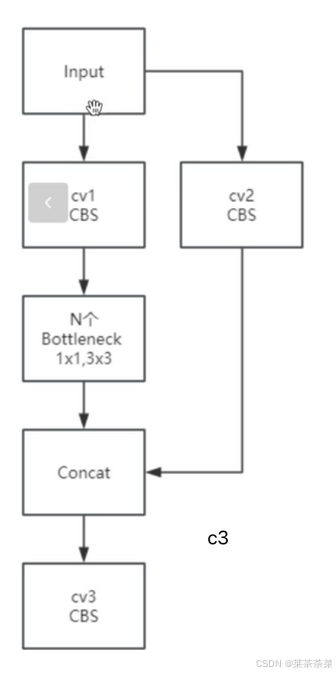
上图是传统c3网络，下面是yolo26的改进

Input

├─ cv1 → Bottleneck × N ┐

├─ cv2 ───────────┼─ Concat → cv3

└─ PSA ───────────┘

为什么要这么做呢，有什么优势？

动机 1 ：局部几何 + 全局语义解耦

Bottleneck：→ 边缘 / 形状 / 几何

PSA：→ 目标整体 / 上下文 / 位置关系，并行比串行更稳定

动机 2 ：替代 DFL 之后，回归更吃"结构感"

YOLOv26 取消 DFL，用连续回归

那就意味着：模型更依赖特征本身的几何一致性，PSA 在 block 级别提供"全局约束"

动机 3 ：为 anchor-free 回归提供全局参考

anchor-free 的 ltrb 回归：l, t, r, b = f(feature)，PSA 能显著减少：局部歧义、尺度漂移、边界不一致

Bottleneck它学到的结构是：

• 边缘连续
• 局部纹理一致
• 邻域几何平滑
• 它只知道："我附近长得像什么"

DFL 被移除之后，少掉的是「隐式几何约束」，PSA提供的是「目标级空间先验」，即"哪些空间位置，应该在当前 feature 中被整体关注 "，这隐含了一个非常重要的信息：目标的"空间占据范围"，这正是回归所缺失、而 Bottleneck 无法提供的。

ProgLoss（渐进损失平衡）

在目标检测（尤其是 YOLO / anchor-free）中，损失项本身是异构的：

L=λclsLcls+λboxLbox+λobjLobjλ_{cls}L_{cls}+λ_{box}L_{box}+λ_{obj}L_{obj}λclsLcls+λboxLbox+λobjLobj

它的问题是：

1.固定 loss 权重

• early stage：box 回归噪声极大 → box loss 主导梯度
• late stage：cls / obj 成为瓶颈

2.不同 loss 收敛速度不同

• cls 很快下降
• box（尤其 IoU 系）下降慢、梯度不稳定

3.正负样本比例随训练动态变化

• 初期：正样本稀疏，objectness 极难
• 后期：大量 easy negative

以 YOLO 的 obj / cls 为例：每一个 grid,每一个 stride,每一个正样本 + 大量负样本, 几乎所有位置都会产生梯度。

而 box 回归是：只有 正样本,且 IoU 有 threshold / assign,BCE 是"全图参与反向传播",回归是"稀疏参与"。

ProgLoss是在不同训练阶段，自动调整各 loss 的"话语权"

阶段	网络能力	主要目标
Early	表达能力弱	先学"在哪里有物体"
Mid	定位逐渐稳定	精调 box
Late	定位稳定	提升分类与置信度

阶段	Loss 特性	为什么噪声/瓶颈	ProgLoss 处理
Early	box L1 / IoU 大梯度	初始预测离 GT 远 → 梯度方向不稳定	降低 λ_box，先学 obj/cls
Mid	box 与 cls 平衡	box 开始收敛，cls 下降	动态 λ_box 上升
Late	box 小梯度，cls/obj 瓶颈	hard negative、IoU 梯度小	λ_box 保持高，λ_cls/obj mild decay

STAL（小目标感知标签分配）

STAL 本质不是"给小目标更多正样本"，

而是：在 label assignment 阶段，改变"什么叫好预测"的判据，使小目标不再被 IoU / 尺度偏置系统性压制。

• 小目标：

  • IoU 波动大 → cost 大
  • 更容易被挤出 Top-k

• 大目标：

  • IoU 稳 → 稳定进入正样本

不是模型不学小目标，而是 label assignment 阶段就"不给资格"

于是 STAL 引入 size-aware 的 assignment 机制：

GT 越小： IoU 权重 ↓ 几何/中心/尺度一致性权重 ↑ 正样本覆盖范围 ↑

YOLOv26 的 STAL 并不是单一 trick，而是 三层协同设计：

1. 小目标感知的 cost 重加权（最核心）

   设 GT 尺度：

   s=w⋅h

   归一化：
   shat=s/srefs_{hat}= s/s_{ref}shat=s/sref

   定义 小目标权重函数（示意）：
   ω(s)=clamp(1/(shat+ϵ),ωmax)ω(s)=clamp(1/(s_{hat}+ϵ),ω_{max})ω(s)=clamp(1/(shat+ϵ),ωmax)
   结果：目标越小，ω 越大
   
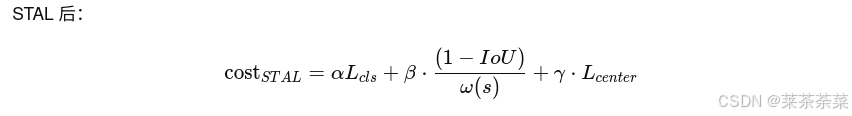
   IoU 的"杀伤力"被 size factor 抑制了

2. 小目标的正样本 Top-k 自适应扩大

   在 TAL 中：每个 GT 选 Top-k predictions（通常 k=10）

   STAL 中：
   k(s)=kbase⋅ω(s)；k(s)=k_{base}⋅ω(s)；k(s)=kbase⋅ω(s)；

   目标尺度	k
   大目标	10
   中目标	15
   小目标	20~30

   这样就相当于小目标有了召回补偿，扩大候选集合。

3. 中心一致性 / 几何先验的显式引入
   
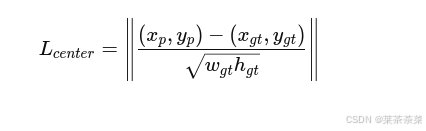
   对于小目标惩罚更重 ：

   大目标：偏 2px → 相对位置变化很小

   小目标：偏 2px → 可能直接错位

ProgLoss：loss 权重在变

STAL：正样本结构在变

MuSGD

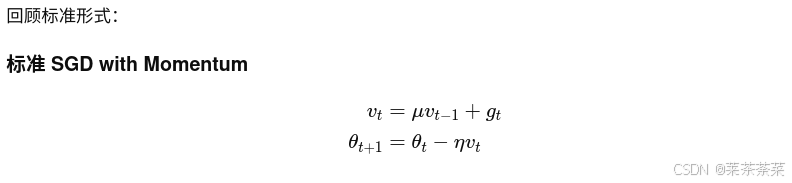
YOLOv26 同时做了三件会破坏优化稳定性的事：

• 取消 DFL → box 回归从"分布期望"变成"连续值"，early 梯度方向抖动明显
• STAL → 正样本集合随 GT 尺度动态变化，每个 iter 的梯度统计分布在变
• ProgLoss → loss 权重随训练进度变化，同一参数在不同阶段"被谁驱动"不一样

梯度分布是强非平稳的，固定 μ 的 SGD / AdamW 都会出现问题。

MuSGD的优化：

1. 动量 μ 是随训练进度调度的
   不像之前的固定 momentum= 0.9，yolo26中:

μ(t)=μmin+(μmax−μmin)⋅p(t),p=T/tμ(t)=μ_{min}+(μ_{max}−μ_{min})⋅p(t), p=T/tμ(t)=μmin+(μmax−μmin)⋅p(t),p=T/t

阶段	μ	原因
early	小	梯度方向噪声大，不要"记仇"
mid	上升	方向开始稳定
late	大	平滑收敛、防抖

2. 梯度幅值去敏（Magnitude-Unified）
   YOLOv26 中不是直接用 gtg_tgt，而是：
   
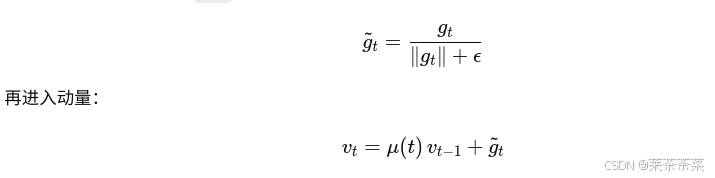
   | 项 | BCE（cls/obj） | box / IoU |
   | --------- | ------------ | --------- |
   | 参与位置 | 全图 | 仅正样本 |
   | 梯度符号 | 稳定 | 易翻转 |
   | 梯度是否连续 | ✔ | ❌（IoU 截断） |
   | early 稳定性 | 高 | 低 |

所以 late stage 的瓶颈一定在 cls / obj

用归一化后的 g tg~tg t:

cls / obj 不再因为量级大而压制其他任务

box 的"方向贡献"被保留
这是 跨 task 的梯度公平化

特点	BCE
梯度是否稀疏	❌ 否
单点梯度幅值	(\le 1)
累积梯度规模	非常大