从零手写Transformer：基于每一步shape变化拆解与PyTorch实现

本文将用PyTorch从零实现一个完整的Transformer模型，并通过张量形状变化和广播机制详解其内部工作原理。

1. 缩放点积注意力（Scaled Dot-Product Attention）

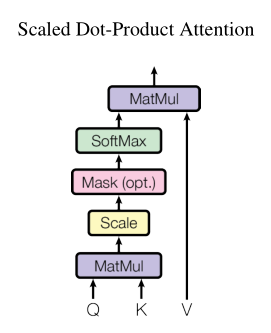
想象你在图书馆找资料：Query 是你提出的问题，Key 是每本书的标签，Value是书里的内容。

• 点积：计算问题与标签的匹配程度（相似度）
• 缩放：防止维度太高时点积结果爆炸（除以√d_k）
• Softmax：把匹配度转换成概率（总和为100%）
• Mask：把不需要看的书（Padding或未来词）屏蔽掉（设为-∞）

代码实现

class ScaledDotProductAttention(nn.Module):
    def __init__(self):
        super().__init__()
    
    def forward(self, Q, K, V, mask=None):
        # 输入: Q, K, V 形状都是 [B, H, L, d_k]
        # B: Batch size, H: 头数, L: 序列长度, d_k: 每头维度
        d_k = Q.size(-1)
        
        # 计算注意力分数: Q·K^T / √d_k
        # [B, H, L, d_k] @ [B, H, d_k, L] → [B, H, L, L]
        # 结果[L, L]矩阵表示每个词对其他词的关注程度
        scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(d_k)

        if mask is not None:
            # Mask广播: [B, 1, L, L] → [B, H, L, L] (H维自动复制)
            # 将mask为0的位置填充-1e9，softmax后变为0
            scores = scores.masked_fill(mask == 0, -1e9)
        
        # Softmax在最后一个维度(L)计算，每行之和为1
        attn = torch.softmax(scores, dim=-1)  # [B, H, L, L]
        
        # 加权求和: 注意力权重 @ 值向量
        # [B, H, L, L] @ [B, H, L, d_k] → [B, H, L, d_k]
        output = torch.matmul(attn, V)
        return output, attn

形状变化流程图：

Q/K/V: [B, H, L, d_k]
    ↓
Q·K^T: [B, H, L, L]  (注意力分数矩阵，第i行第j列表示第i个词对第j个词的关注度)
    ↓
Softmax: [B, H, L, L]  (每行归一化为概率分布)
    ↓
Attn·V: [B, H, L, d_k]  (加权后的特征表示)

---

2. 多头注意力（Multi-Head Attention）

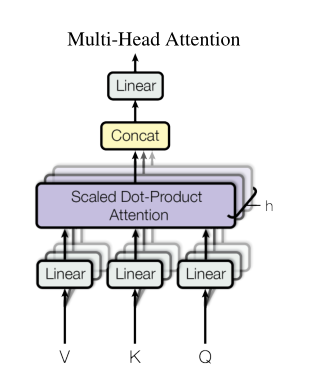
一个人看问题的角度有限，多头注意力就像召集H个专家，每人从不同角度（子空间）分析同一句话，最后汇总意见。

• Linear投影：用 learned 的矩阵把输入映射到不同子空间
• Split Heads：把大向量切成H份，每份d_k维度（类似分组讨论）
• Concat Heads：把H个专家的意见拼接回原始维度

代码实现

class MultiHeadAttention(nn.Module):
    def __init__(self, d_model, n_heads):
        super().__init__()
        assert d_model % n_heads == 0
        
        self.d_model = d_model  # 模型总维度 D
        self.n_heads = n_heads  # 头数 H
        self.d_k = d_model // n_heads  # 每头维度 d_k = D/H

        # 四个线性投影矩阵: Q, K, V 投影 + 最终输出投影
        self.W_q = nn.Linear(d_model, d_model)
        self.W_k = nn.Linear(d_model, d_model)
        self.W_v = nn.Linear(d_model, d_model)
        self.fc = nn.Linear(d_model, d_model)

        self.attn = ScaledDotProductAttention()

    def forward(self, q, k, v, mask=None):
        B, L, _ = q.size()  # 输入: [B, L, D]

        # 1. 线性投影并分头
        # [B, L, D] → Linear → [B, L, D] → View → [B, L, H, d_k]
        Q = self.W_q(q).view(B, L, self.n_heads, self.d_k)
        K = self.W_k(k).view(B, L, self.n_heads, self.d_k)
        V = self.W_v(v).view(B, L, self.n_heads, self.d_k)

        # 2. 调整维度准备并行计算
        # [B, L, H, d_k] → Transpose → [B, H, L, d_k]
        # 现在H和L交换位置，方便在L维度上做注意力计算
        Q, K, V = Q.transpose(1, 2), K.transpose(1, 2), V.transpose(1, 2)

        # 3. 计算注意力
        out, attn = self.attn(Q, K, V, mask)  # out: [B, H, L, d_k]

        # 4. 合并多头结果
        # Transpose: [B, H, L, d_k] → [B, L, H, d_k]
        # View: [B, L, H, d_k] → [B, L, D] (H*d_k=D，拼接所有头)
        out = out.transpose(1, 2).contiguous().view(B, L, self.d_model)
        
        return self.fc(out)  # 最终线性投影: [B, L, D]

分头合并可视化：

输入: [B, L, D] --投影--> [B, L, D]
            ↓ View
       [B, L, H, d_k]  (像把D维切成H个小段)
            ↓ Transpose
       [B, H, L, d_k]  (H个头并行处理)
            ↓ Attention
       [B, H, L, d_k]
            ↓ Transpose+View
       [B, L, D]  (合并所有头的见解)

---

3. 前馈网络（Feed Forward）

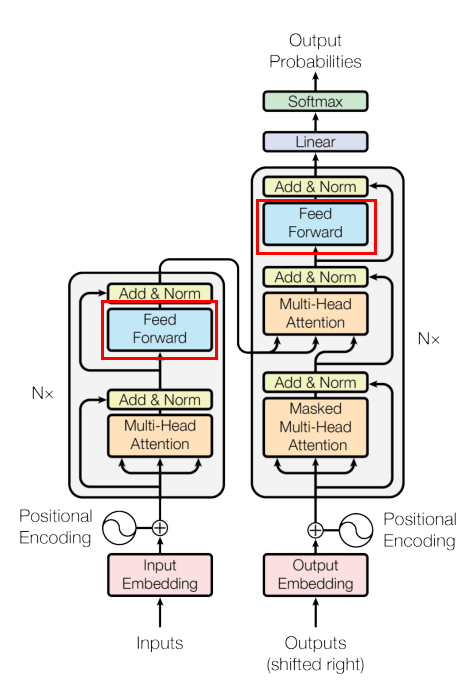
注意力机制提取了上下文关系后，前馈网络对每个位置独立做非线性变换（类似每个词根据自己的上下文表示做深入思考）。

结构：线性扩张 → ReLU激活 → 线性压缩（D → d_ffn → D）

代码实现

class FeedForward(nn.Module):
    def __init__(self, d_model, d_ffn):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(d_model, d_ffn),   # [B, L, D] → [B, L, d_ffn] (扩张4倍左右)
            nn.ReLU(),                    # 非线性激活
            nn.Linear(d_ffn, d_model)    # [B, L, d_ffn] → [B, L, D] (压缩回原维度)
        )
    
    def forward(self, x):
        return self.net(x)  # [B, L, D]

---

4. 层归一化（Layer Normalization）

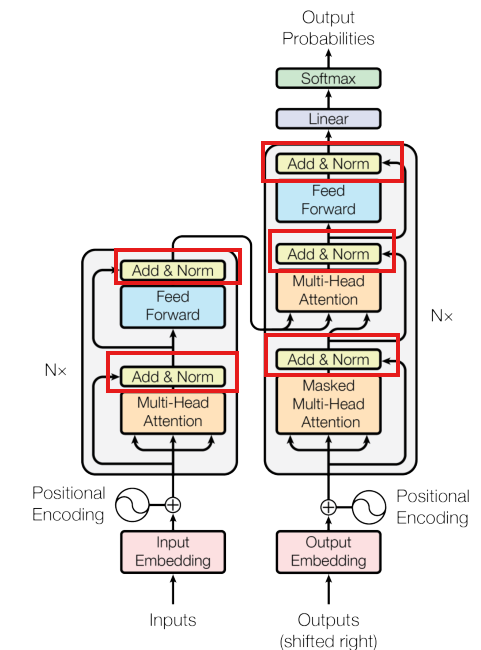
深度网络中数据分布会漂移（Internal Covariate Shift）。层归一化把每句话的特征归一化为标准分布（均值0，方差1），让训练更稳定。

• gamma/beta：可学习的缩放和平移参数。如果归一化破坏了有用信息，网络可以通过学习恢复（gamma=σ, beta=μ）。

代码实现

class LayerNorm(nn.Module):
    def __init__(self, d_model, eps=1e-12):
        super().__init__()
        # 可学习参数，初始gamma=1(不缩放)，beta=0(不平移)
        self.gamma = nn.Parameter(torch.ones(d_model))    # [D]
        self.beta = nn.Parameter(torch.zeros(d_model))    # [D]
        self.eps = eps  # 防止除0

    def forward(self, x):
        # x: [B, L, D]
        # 在最后一维(D)计算均值和方差，保持维度用于广播
        mean = x.mean(-1, keepdim=True)      # [B, L, 1]
        var = x.var(-1, unbiased=False, keepdim=True)   # [B, L, 1]
        
        # 广播过程1: 
        # x: [B, L, D] - mean: [B, L, 1] → mean广播为[B, L, D]后相减
        out = (x - mean) / math.sqrt(var + self.eps)   # [B, L, D]
        
        # 广播过程2:
        # gamma: [D] → 自动广播为 [B, L, D]
        # beta: [D] → 自动广播为 [B, L, D]
        out = self.gamma * out + self.beta   # [B, L, D]
        return out

---

5. 位置编码（Positional Encoding）

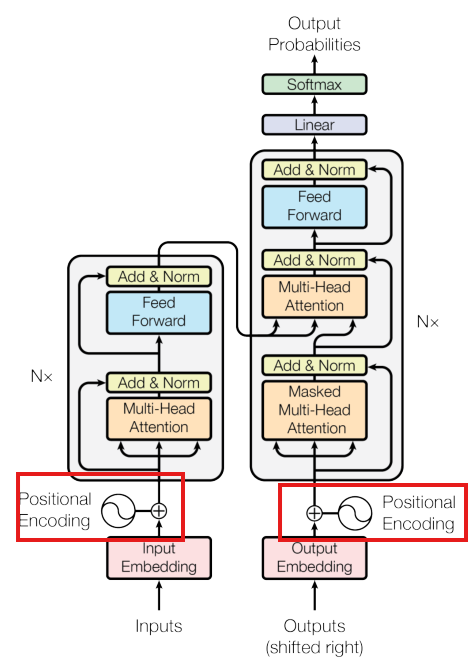
Transformer没有RNN的时序概念，需要位置编码给每个词注入"位置信息"。使用不同频率的正弦/余弦函数：

• 低维度：变化缓慢（捕捉长距离位置关系）
• 高维度：变化快速（捕捉精细位置差异）

代码实现

class PositionalEncoding(nn.Module):
    def __init__(self, d_model, max_len=5000):
        super().__init__()
        pe = torch.zeros(max_len, d_model)  # [max_len, D]
        
        # pos: [max_len, 1] - 位置索引列向量 [0,1,2...4999]^T
        pos = torch.arange(0, max_len).unsqueeze(1)
        
        # div_term: [D/2] - 频率衰减项，指数递减
        div = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model))
        
        # 广播计算: pos([max_len,1]) * div([D/2]) → [max_len, D/2]
        # 偶数维用sin，奇数维用cos
        pe[:, 0::2] = torch.sin(pos * div)   # [max_len, D/2]
        pe[:, 1::2] = torch.cos(pos * div)   # [max_len, D/2]
        
        # 注册为buffer: [1, max_len, D]，第0维为batch维度
        self.register_buffer("pe", pe.unsqueeze(0))

    def forward(self, x):
        # x: [B, L, D]
        # self.pe[:, :L]: [1, L, D]
        # 广播相加: [B, L, D] + [1, L, D] → [B, L, D]
        # pe在batch维广播，自动复制到所有样本
        return x + self.pe[:, :x.size(1)]

位置编码模式可视化（d_model=8, max_len=10）：

位置0: [sin(0), cos(0), sin(0), cos(0)...]  低频
位置1: [sin(1/10000^0), cos(1/10000^0), ...]  稍高频率
...
位置9: [sin(9/10000^(6/8)), ...]  高频波动

---

6. 掩码（Mask）

• Padding Mask ：屏蔽填充符（<pad>），让模型不要关注无意义的填充。
• Causal Mask：解码器用，防止偷看未来词（只能看已生成的词）。

代码实现

class Mask_Address:
    def make_src_mask(self, src):
        # src: [B, L]
        # 非零位置为True(有效词)，零位置为False(Padding)
        return (src != 0).unsqueeze(1).unsqueeze(2)  # [B, 1, 1, L]
    
    def make_tgt_mask(self, tgt):
        B, L = tgt.size()
        # Padding掩码: [B, 1, 1, L]
        pad_mask = (tgt != 0).unsqueeze(1).unsqueeze(2)
        
        # 因果掩码（下三角）: [L, L]，上三角为False
        causal_mask = torch.tril(torch.ones(L, L)).bool()
        
        # 广播与运算:
        # pad_mask: [B, 1, 1, L] → 广播为 [B, 1, L, L]
        # causal_mask: [L, L] → 广播为 [B, 1, L, L]
        # 结果: 必须同时满足"非填充"且"不越界"
        return pad_mask & causal_mask  # [B, 1, L, L]

掩码可视化（L=4）：

Padding Mask (假设第3、4位是padding):
[1, 1, 0, 0]
[1, 1, 0, 0]
[1, 1, 0, 0]
[1, 1, 0, 0]

Causal Mask:
[1, 0, 0, 0]  (第1词只能看自己)
[1, 1, 0, 0]  (第2词能看前2个)
[1, 1, 1, 0]  (第3词能看前3个)
[1, 1, 1, 1]  (第4词能看全部)

Combined (逐元素与):
[1, 0, 0, 0]
[1, 1, 0, 0]
[1, 1, 0, 0]  (第3行被padding限制)
[1, 1, 0, 0]  (第4行被padding限制)

---

7. 编解码器层（Encoder/Decoder Layer）

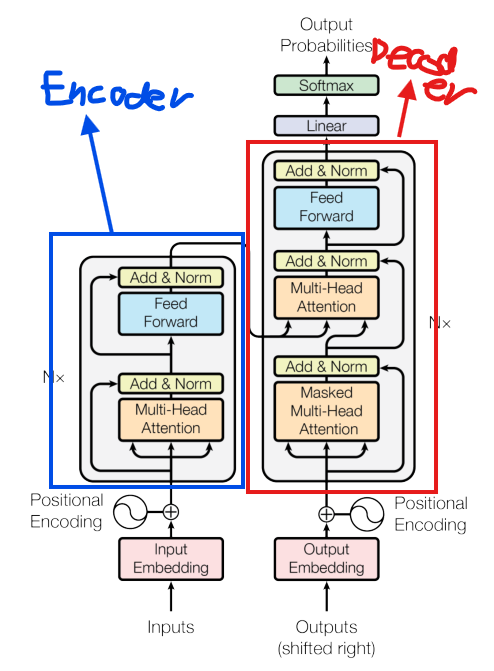
• 编码器：自注意力提取输入特征 → 残差连接+归一化 → 前馈网络 → 残差连接+归一化
• 解码器： masked自注意力（看不到未来）→ 交叉注意力（看编码器输出）→ 前馈网络，每层都有残差连接

代码实现

class EncoderLayer(nn.Module):
    def __init__(self, d_model, n_heads, d_ffn):
        super().__init__()
        self.self_attn = MultiHeadAttention(d_model, n_heads)
        self.ffn = FeedForward(d_model, d_ffn)
        self.norm1 = nn.LayerNorm(d_model)
        self.norm2 = nn.LayerNorm(d_model)

    def forward(self, x, src_mask):
        # 子层1: 多头自注意力 + 残差连接 + 层归一化
        # x + self_attn(x): 残差连接防止梯度消失
        x = self.norm1(x + self.self_attn(x, x, x, src_mask))  # [B, L, D]
        
        # 子层2: 前馈网络 + 残差连接 + 层归一化
        x = self.norm2(x + self.ffn(x))  # [B, L, D]
        return x

class DecoderLayer(nn.Module):
    def __init__(self, d_model, n_heads, d_ffn):
        super().__init__()
        self.self_attn = MultiHeadAttention(d_model, n_heads)   # 自注意力
        self.enc_attn = MultiHeadAttention(d_model, n_heads)    # 交叉注意力
        self.ffn = FeedForward(d_model, d_ffn)
        self.norm1 = nn.LayerNorm(d_model)
        self.norm2 = nn.LayerNorm(d_model)
        self.norm3 = nn.LayerNorm(d_model)

    def forward(self, x, enc_out, tgt_mask, src_mask):
        # 子层1: Masked Self-Attention（只能看已生成的词）
        x = self.norm1(x + self.self_attn(x, x, x, tgt_mask))
        
        # 子层2: Cross-Attention（Q来自解码器，K/V来自编码器）
        # x作为Query，去查询enc_out的Key和Value
        x = self.norm2(x + self.enc_attn(x, enc_out, enc_out, src_mask))
        
        # 子层3: Feed Forward
        x = self.norm3(x + self.ffn(x))
        return x  # [B, L, D]

---

8. 完整Transformer模型

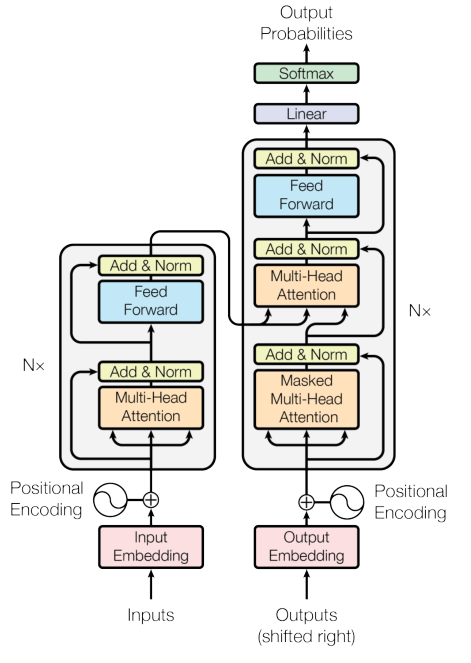
组装所有组件：

1. 嵌入层：把整数ID变成向量
2. 位置编码：加上位置信息
3. N层编码器：提取输入特征
4. N层解码器：生成输出序列
5. 输出投影：映射到词表维度（预测下一个词）

代码实现

class Transformer(nn.Module):
    def __init__(self, vocab_size, d_model, n_heads, d_ffn, n_layers):
        super().__init__()
        # 词嵌入: [B, L] → [B, L, D]
        self.emb = nn.Embedding(vocab_size, d_model)
        self.pos = PositionalEncoding(d_model)
        self.mask_address = Mask_Address()
        
        # 堆叠N层编码器和解码器
        self.encoder = nn.ModuleList([
            EncoderLayer(d_model, n_heads, d_ffn) for _ in range(n_layers)
        ])
        self.decoder = nn.ModuleList([
            DecoderLayer(d_model, n_heads, d_ffn) for _ in range(n_layers)
        ])
        
        # 输出投影到词表: [B, L, D] → [B, L, V]
        self.fc_out = nn.Linear(d_model, vocab_size)

    def forward(self, src, tgt):
        # 生成掩码
        src_mask = self.mask_address.make_src_mask(src)  # [B, 1, 1, L_src]
        tgt_mask = self.mask_address.make_tgt_mask(tgt)  # [B, 1, L_tgt, L_tgt]
        
        # 编码器路径
        enc = self.pos(self.emb(src))  # [B, L_src, D]
        for layer in self.encoder:
            enc = layer(enc, src_mask)  # [B, L_src, D]
        
        # 解码器路径
        dec = self.pos(self.emb(tgt))  # [B, L_tgt, D]
        for layer in self.decoder:
            # dec: [B, L_tgt, D], enc: [B, L_src, D]
            dec = layer(dec, enc, tgt_mask, src_mask)  # [B, L_tgt, D]
        
        return self.fc_out(dec)  # [B, L_tgt, V]

整体数据流：

src: [B, L_src] --emb+pos--> [B, L_src, D] --Encoder×N--> [B, L_src, D] (enc)
                                                    ↓
tgt: [B, L_tgt] --emb+pos--> [B, L_tgt, D] --Decoder×N--> [B, L_tgt, D] (dec)
                                                    ↓
                                              fc_out: [B, L_tgt, V]
                                                    ↓
                                             Softmax → 词表概率分布

---

总结

通过本文，我们实现了完整的Transformer架构：

1. 注意力机制通过Q/K/V三元组计算词间依赖
2. 多头机制并行捕捉不同子空间特征
3. 位置编码注入时序信息
4. 掩码处理变长序列和自回归生成
5. 残差连接和层归一化稳定深层网络训练

理解这些张量形状[B, H, L, D]的变化和广播机制，是掌握Transformer实现的关键。

引用：

@misc{vaswani2023attentionneed,

title={Attention Is All You Need},

author={Ashish Vaswani and Noam Shazeer and Niki Parmar and Jakob Uszkoreit and Llion Jones and Aidan N. Gomez and Lukasz Kaiser and Illia Polosukhin},

year={2023},

eprint={1706.03762},

archivePrefix={arXiv},

primaryClass={cs.CL},

url={https://arxiv.org/abs/1706.03762},

}