数据结构与算法 | 完全二叉树的实现、哈希表的实现

今天，将继续上次的二叉树的讲解，前面已经将二叉树的基本概念讲清楚了，我们接着就是去搞清楚如何实现二叉树，及其常用用法的基础实现，那我们就开始吧：

1、完全二叉树的实现

1.1 结构体的构建

对于二叉树而言，都是一个一个的节点，可以用数组来构建，也可以用链式存储，我们就用链表的设计方法来构建，数组存储很简单，加上我们昨天学习的它的特点，就可以根据下标得到它的左孩子和右孩子，所以我们就不讲这种方法了。

cs 复制代码

typedef struct TreeNode {
    int no;    //该节点的序号
    struct TreeNode *LeftChild;
    struct TreeNode *RightChild;
}TreeNode;

如果需要在节点里面存放数据，我们可以继续在结构体里面添加成员变量，是比较灵活的。

1.2 完全二叉树的构建

在我们知道有多少个节点的情况下，我们可以这么构建：

cs 复制代码

TreeNode *CreateCompleteBTree(int StartNo, int EndNo) {
    if(StartNo > EndNo) return NULL;
    TreeNode *newNode = NULL;
    newNode = malloc(sizeof(TreeNode));
    if(newNode == NULL) {
        perror("malloc newNode failed");
        return NULL;
    }
    
    newNode->no = StartNo;
    newNode->LeftChild = CreateCompleteBTree(StartNo * 2, EndNo);
    newNode->RightCild = CreateCompleteBTree(StartNo * 2 + 1, EndNo);
    
    return newNode;
}

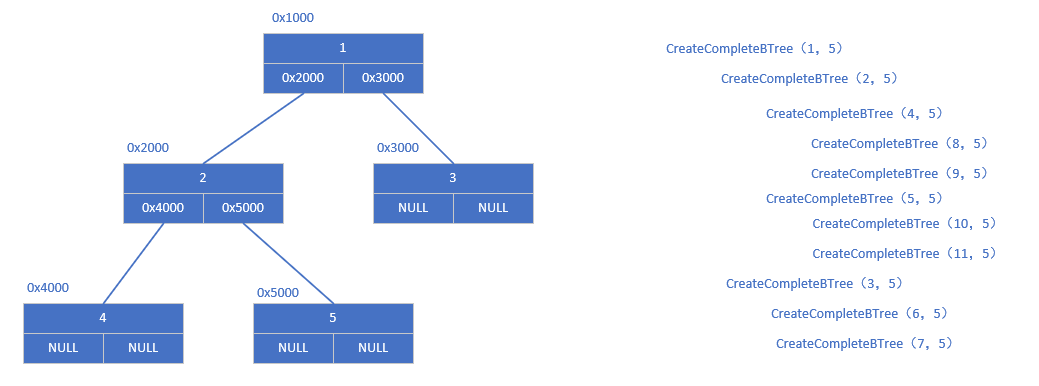
如果大家看代码还是不太理解的话，可以参考下图，就知道是怎么一步一步递归创建的了。

这种创建方法就是用前序遍历的思想实现的。

如果我们不知道的情况 下，或者不是一个完全二叉树 的时候，也就是没有规律的二叉树时，上面的方法就不适用了，我们也可以通过下述方法进行构建：

cs 复制代码

TreeNode *CreateBTree(int StartNo) {
    TreeNode *newNode = NULL;
    char ch = 0;
    scanf(" %c", &ch);
    if(ch == '#') {
        return NULL;
    }else {
        newNode = malloc(sizeof(TreeNode));
        if(newNode == NULL) {
            perror("malloc newNode failed");
            return NULL;
        }
        newNode->no = no;
        newNode->data = ch;
        newNode->LeftChild = CreateBTree(2 * no);
        newNode->RightChild = CreateBTree(2 * no + 1);
    }
    return 0;
}

在这里我们又定义了一个结构体成员变量，char data; 方便我们用来存储写入的数据，还有一点需要注意的是：我们一般用'#'表示空节点。

1.3 前序遍历

1.3.1 递归遍历

cs 复制代码

int PreOrderBtree(TreeNode *root) {
	if(root == NULL) return 0;

	printf("%d ", root->no);
	PreOrderBtree(root->LeftChild);
	PreOrderBtree(root->RightChild);

	return 0;
}

对于前序遍历我们只要记住是先根节点，在左节点，最后右节点，就很清晰可见了。

递归的方法也是比较简单，容易理解的。

1.3.2非递归

我们都知道这三种遍历都是深度优先，对于深度优先我们一般用栈遍历，先进后出的思想。

cs 复制代码

int PreOrderBTreeBySeqStack(TreeNode *root) {
	TreeNode **Stack = malloc(sizeof(TreeNode *) * 50);
	TreeNode *tmpNode = root;
	int top = -1;

	while(tmpNode || top >= 0) {
		while(tmpNode) {
			printf("%d ", tmpNode->no);
			Stack[++top] = tmpNode;
			tmpNode = tmpNode->LeftChild;
		}
		if(top < 0) break;
		tmpNode = Stack[top--];
		tmpNode = tmpNode->RightChild;
	}
	free(Stack);
	Stack = NULL;
	return 0;
}

这里采用了顺序栈进行遍历，大致思路：

就是先定义一个栈，然后先用一个指针指向根节点，然后进入循环，外层循环除了用上述的方法外，还可以直接用一个死循环进行遍历，里面通过判断顺序栈是否为空，进行退出，进入第二层循环，我们先打印根节点，在将节点存入栈中，然后遍历左孩子，一直到某一节点没有左孩子为止，退出内层循环，此时栈里存放的都是左节点，在判断栈是否为空，不为空，我们就取出栈顶数据，然后在取它的右孩子，如果有的话，会再次进入内层循环，在打印，此时因为根节点和左节点已经打印了，所以打印右节点，然后继续找右孩子的左孩子，直到没有左孩子为止，直到最后栈空，退出，表示遍历结束。

1.4 中序遍历

1.4.1 递归遍历

cs 复制代码

int InOrderBTree(TreeNode *root) {
	if(root == NULL) return 0;
	InOrderBTree(root->LeftChild);
	printf("%d ", root->no);
	InOrderBTree(root->RightChild);

	return 0;
}

与前序遍历的递归方法也是一样的，只是打印的位置放到了遍历左孩子的下面，也就是打印左节点。

1.4.2非递归

cs 复制代码

int InOrderBTreeBySeqStqck(TreeNode *root) {
	TreeNode **Stack = malloc(sizeof(TreeNode *) * 50);
	TreeNode *tmpNode = root;
	int top = -1;
	while(tmpNode || top >= 0) {
		while(tmpNode) {
			Stack[++top] = tmpNode;
			tmpNode = tmpNode->LeftChild;
		}
		if(top < 0) break;
		tmpNode = Stack[top--];
		printf("%d ", tmpNode->no);
		tmpNode = tmpNode->RightChild;
	}
	free(Stack);
	Stack = NULL;
	return 0;
}

中序和前序是差不多的思路，只是打印是在每次从栈中取出数据时进行打印，其他都是一样的。

1.5 后序遍历

1.5.1 递归遍历

cs 复制代码

int PostOrderBTree(TreeNode *root) {
	if(root == NULL) return 0;
	PostOrderBTree(root->LeftChild);
	PostOrderBTree(root->RightChild);
	printf("%d ", root->no);
	return 0;
}

可以看到，后序遍历打印放到了最下面，就是先左在右，最后根节点，这里就相当于把每个节点看成一个根节点，直到没有孩子就打印它。

1.5.2非递归

对于后序遍历来说会有一点麻烦，因为要先左在右，最后在根节点，这里给大家说下三种形式去实现吧，先来个简单的，

（1）通过双栈去实现

因为我们知道，后序遍历是左右根，放在栈里就是根右左，是不是和前序遍历的根左右很类似呢，那我们如何用双栈去实现第二个栈是根右左的顺序放进去呢，对于第一个栈，我们拆分一下，回想上面层序遍历的队列进入方式，我们先让根节点进入，然后取出放在第二个栈中，我们就实现了根先进入了，之后在让这个根节点的左右孩子依次进入栈中，如果有的话，然后下次再取出时，是不是就先取出的是右节点，然后在放入右孩子的左右孩子，依次往复，直到所有节点都放在了第二个栈中，在从第二个栈中依次取出，就是我们所要的后序遍历了。

cs 复制代码

int PostOrderBTreeByTwoStacks(TreeNode *root) {
	TreeNode **Stack1 = NULL;
	TreeNode **Stack2 = NULL;
	Stack1 = malloc(sizeof(TreeNode *) * 50);
	Stack2 = malloc(sizeof(TreeNode *) * 50);
	int top1 = -1;
	int top2 = -1;
	Stack1[++top1] = root;
	while(top1 >= 0) {
		TreeNode *node = Stack1[top1--];
		Stack2[++top2] = node;
		if(node->LeftChild) {
			Stack1[++top1] = node->LeftChild;
		}
		if(node->RightChild) {
			Stack1[++top1] = node->RightChild;
		}
	}
	while(top2 >= 0) {
		TreeNode *node = Stack2[top2--];
		printf("%d ", node->no);
	}

	printf("\n");
	free(Stack1);
	free(Stack2);

	return 0;
}

（2）单栈加一指针实现

cs 复制代码

int PostOrderBTreeByPointer(TreeNode *root) {
	TreeNode **Stack = malloc(sizeof(TreeNode *) * 50);
	int top = -1;
	TreeNode *lastVisited = NULL;
	TreeNode *tmpNode = root;
	while(tmpNode || top >= 0) {
		while(ctmpNode) {
			Stack[++top] = tmpNode;
			tmpNode = tmpNode->LeftChild;
		}

		if(top < 0) break;
		tmpNode = Stack[top];
		if(tmpNode->RightChild && tmpNode->RightChild != lastVisited) {
			tmpNode = tmpNode->RightChild;
		} else {
			printf("%d ", tmpNode->no);
			lastVisited = tmpNode;
			top--;
		}
	}

	printf("\n");
	free(Stack);
}

这里和上面前序和中序的方法是类似的，只不过加了个前置条件，我们加入了一个上一次已经打印过的节点，同时在这里，我们没有先出栈，而是先找到栈顶元素，然后判断它是否有右孩子，同时该右孩子是否是上一次打印过的，这样就能先打印右孩子，在打印该节点了，如果还像之前那样不加判断的话，就只能实现中序了。

（3）已有顺序栈的前提下

cs 复制代码

int PostOrderBTreeByStack(TreeNode *root) {
	SeqStack *tmpStack = NULL;
	TreeNode *tmpNode = NULL;

	tmpStack = CreateSeqStack(50);
	tmpNode = root;
	while(1) {
		while(tmpNode) {
			tmpNode->flag = 1;
			PushSeqStack(tmpStack, tmpNode);
			tmpNode = tmpNode->LeftChild;
		}
		if(IsEmptySeqStack(tmpStack)) break;
		
		tmpNode = PopSeqStack(tmpStack);
		if(tmpNode->flag) {
			tmpNode->flag = 0;
			PushSeqStack(tmpStack, tmpNode);
			tmpNode = tmpNode->RightChild;
		}else {
			printf("%d ", tmpNode->no);
			tmpNode = NULL;
		}

	}

	DestroySeqStack(&tmpStack);

	return 0;
}

在这里如果我们有获取栈顶元素的函数，还是可以用一指针和第二种方法一样去遍历，如果只有出栈的一个函数的话，我们在这里又得给这个二叉树的结构体添加一个flag标志的一个成员变量了，用它来判断该节点几次进入栈中了，什么意思呢？

也就是说，我们在每个节点第一次进栈时，让flag = 1，也就标志着该节点进入过一次栈，然后在出站时，接收该节点，判断flag是否为1，如果为1，我们给它置为0，表示第二次入栈了，然后遍历它的右孩子，如果为空，不会进入循环，回到退栈这里，再次接收该节点，就是flag=0，此时就表示两次进栈了，就打印它，然后在去接收下一个退出的节点；如果不为空的时候，我们就会继续遍历这个右孩子的左孩子，在遍历右孩子，这样也就实现了，先左孩子，在右孩子，最后根节点的遍历。

1.6 层序遍历

我们知道层序遍历是广度优先，对于广度优先我们就可以使用队列进行遍历，也就是先进先出的一个思想，代码如下：

cs 复制代码

int LevelOrderBTreeBySeqQueue(TreeNode *root, int len) {
	if(root == NULL) {
		printf("二叉树为空\n");
		return 0;
	}
	TreeNode **queue = malloc(sizeof(TreeNode *) * (len + 1));
	int head = 0;
	int tail = 0;
	queue[tail++] = root;
	while(head < tail) {
		TreeNode *curr = queue[head++];
		printf("%d ", curr->no);
		if(curr->LeftChild != NULL) {
			queue[tail++] = curr->LeftChild;
		}
		if(curr->RightChild != NULL) {
			queue[tail++] = curr->RightChild;
		}

	}
	printf("\n");
	free(queue);
	queue = NULL;

	return 0;
}

在这里我们使用的顺序队列去实现的，如果你有一个现成的链队列的话，我们使用链队列也比较方便，如果没有，就用顺序队列就好。

在这里，我们就先让根节点进入队列，然后进入while循环，先用一个指针接收它出队列，并打印，然后它有左孩子，右孩子，在依次入队，每次出一个，就判读有无左孩子和右孩子，有就进入队列，没有就跳过，知道head = tail 时为空，遍历结束，最后在free掉堆区申请的空间，就完成了层序遍历。

1.7 获取二叉树的高度

对于二叉树的高度的获取，我们同样采取的是递归的思想来完成。

cs 复制代码

int GetBTreeHigh(TreeNode *root) {
	int leftHigh = 0;
	int rightHigh = 0;
	if(root == NULL) {
		return 0;
	}

	leftHigh = GetBTreeHigh(root->LeftChild);
	rightHigh = GetBTreeHigh(root->RightChild);

	return (leftHigh > rightHigh ? leftHigh : rightHigh) + 1;
}

1.8 二叉树的销毁

cs 复制代码

int DestroyCompleteBTree(TreeNode **root) {
	if(*root == NULL) return 0;
	DestroyCompleteBTree(&(*root)->LeftChild);
	DestroyCompleteBTree(&(*root)->RightChild);
	free(*root);
	*root = NULL;

	return 0;
}

同样采用的递归的思想，用递归操作就会比较清晰明了，简单。

所以我们得要有递归这种思维，能帮我们省下很多事。

以上就是对二叉树的一个具体实现了，我们很容易发现，递归操作的，代码都比较简单，好理解，非递归的就比较麻烦，看不懂，是吧，没关系，我们可以通过画图在去细细分析就会明白了，还有记住：栈和队列的用法，今天又增加了：

栈可以用来实现深度优先遍历；

队列可以用来实现广度优先遍历。

接下来，我们就进行下一个：哈希表的讲解了：

2、哈希表

**哈希：**算法思想，将数据根据哈希算法映射成键值，根据键值来写入或是查找数据，以实现查找数据O(1)时间复杂度

**哈希碰撞（哈希冲突）：**多个数据通过哈希算法映射成同样的键值，说明产生哈希冲突

**链地址法：**数据产生哈希冲突通过在同一键值位置用链表实现多个数据的存储

实现方法： 这里我们以实现将0-100的数据存放到哈希表中为例子，来实现哈希，要实现一一映射 的话，就需要用数组大小为100来实现，那这样的话就没有啥意义了，直接就用普通数组存储就好了，那我们就用**%10来通过个位来存储吧，那这样是不是就需要数组空间大小为10**来存储呢，还有可能出现哈希冲突，所以我们就用链地址法来解决这个问题。

2.1 创建节点结构体

因为用到**链地址法，**我们就使用节点来存储这些数据：

cs 复制代码

typedef struct ListNode {
    int data;
    struct ListNode *next;
}

2.2 创建哈希表

cs 复制代码

static ListNode *HashTable[10];

int InserHashTable(int tmpData) {
	ListNode *newNode = NULL;
	newNode = malloc(sizeof(ListNode));
	if(newNode == NULL) {
		perror("malloc newNode failed");
		return -1;
	}
	newNode->data = tmpData;
	int idx = tmpData % 10;
	ListNode **tmpNode = &HashTable[idx];
	for(; *tmpNode && tmpData > (*tmpNode)->data; tmpNode = &(*tmpNode)->next);
	newNode->next = *tmpNode;
	*tmpNode = newNode;
	return 0;
}

这里因为我们用到了无头节点，需要对头节点进行处理，同时我们是按照数据从小到大的顺序存储的，所以我们用到了二级指针。

2.3 遍历哈希表

cs 复制代码

int ShowHashTable(void) {
	ListNode *tmpNode = NULL;
	for(int i =0; i < 10; i++) {
		printf("%d: ", i);
		tmpNode = HashTable[i];
		while(tmpNode) {
			printf("%2d ", tmpNode->data);
			tmpNode = tmpNode->next;
		}
		printf("\n");
	}

	return 0;
}

2.4 查找某个元素

cs 复制代码

int FindHashTable(int tmpData) {
	int idx = 0;
	idx = tmpData % 10;
	ListNode *tmpNode = HashTable[idx];
	while(tmpNode && tmpNode->data <= tmpData) {
		if(tmpNode->data == tmpData) return 1;
		tmpNode = tmpNode->next;
	}
	return 0;
}

通过键值映射到指定的空间查找，速度很快

2.5 哈希表的销毁

cs 复制代码

int DestroyHashTable(void) {
	ListNode *tmpNode = NULL;
	ListNode *nextNode = NULL;
	for(int i = 0; i < 10; i++) {
		tmpNode = HashTable[i];
		while(tmpNode) {
			nextNode = tmpNode->next;
			free(tmpNode);
			tmpNode = nextNode;
		}
		HashTable[i] = NULL;
	}

	printf("哈希表已成功销毁！\n");
	return 0;

}

好了，以上就是哈希表的一个讲解，其实对于哈希表来说，最重要的就是找到那个映射关系，才会在后面查询时间为O(1)；以及对于无头链表的一个创建。

那我们就先到这里了，下次见！