目录
[2、im2col + 矩阵乘法](#2、im2col + 矩阵乘法)
卷积操作的底层实现方式主要有两种核心思路：直接卷积（滑动窗口） 和im2col + 矩阵乘法。这两种方式在深度学习框架中都有应用，各有优劣。
1、直接卷积（滑动窗口）
这是最直观、最接近数学定义的实现方式。其核心思想是：
- 滑动卷积核：将一个小型的权重矩阵（称为卷积核或滤波器）在输入的特征图（通常是2D图像或3D张量）上滑动。
- 逐元素相乘与求和：在卷积核的每一个位置，将其与输入特征图上被覆盖的对应区域进行逐元素相乘，然后将所有乘积结果相加，得到一个标量值。
- 生成输出：这个标量值就是输出特征图中对应位置的像素值。卷积核按照设定的步长（stride）在输入上移动，直到覆盖整个输入空间，从而生成完整的输出特征图。
这种方式在概念上简单易懂，但当卷积核较大或输入尺寸很大时，计算效率相对较低，因为存在大量的重复计算。
2、im2col + 矩阵乘法
这是一种将卷积操作转化为高效矩阵乘法 的优化方法，是现代深度学习框架（如PyTorch、TensorFlow）底层常用的实现方式。
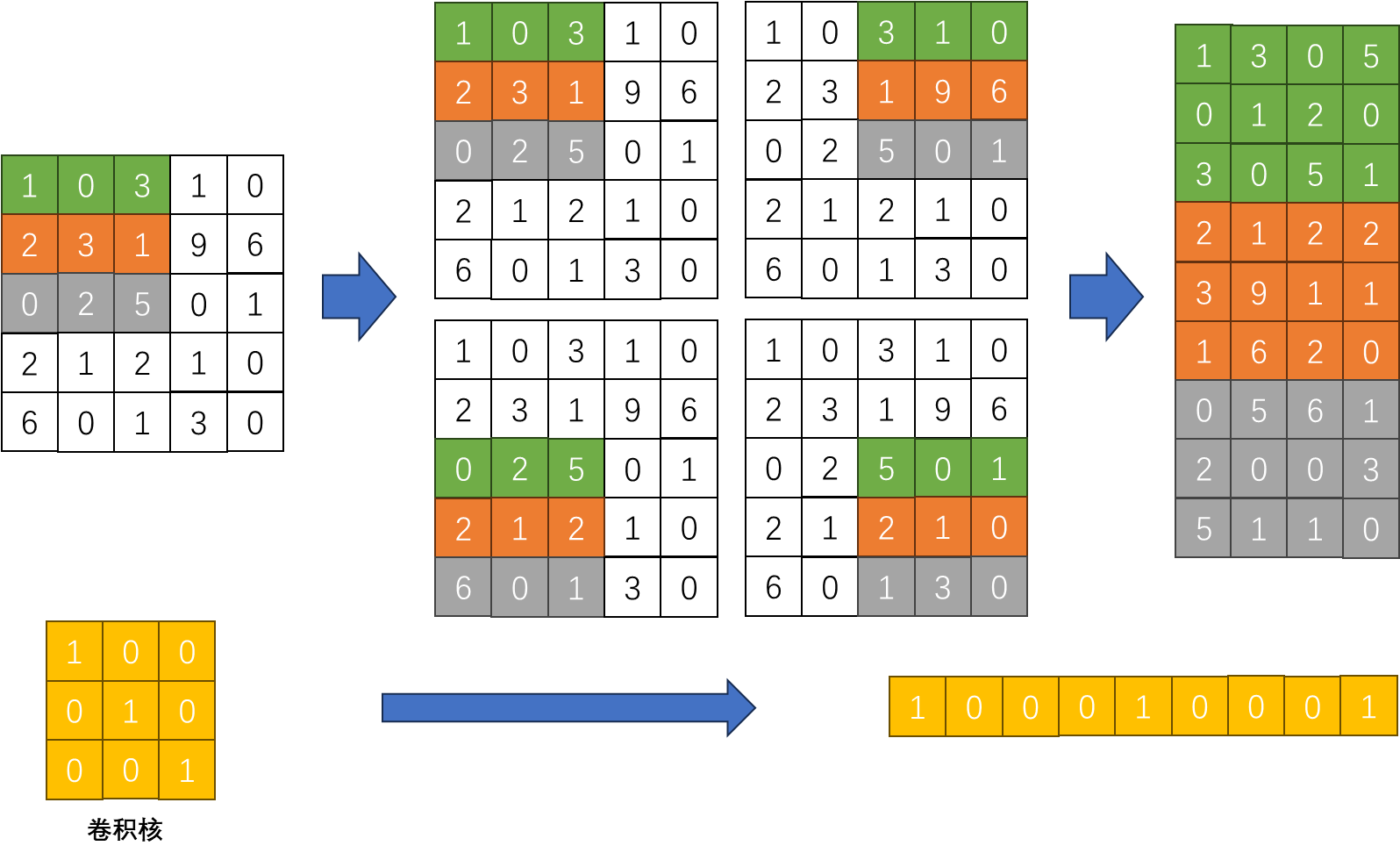im2col
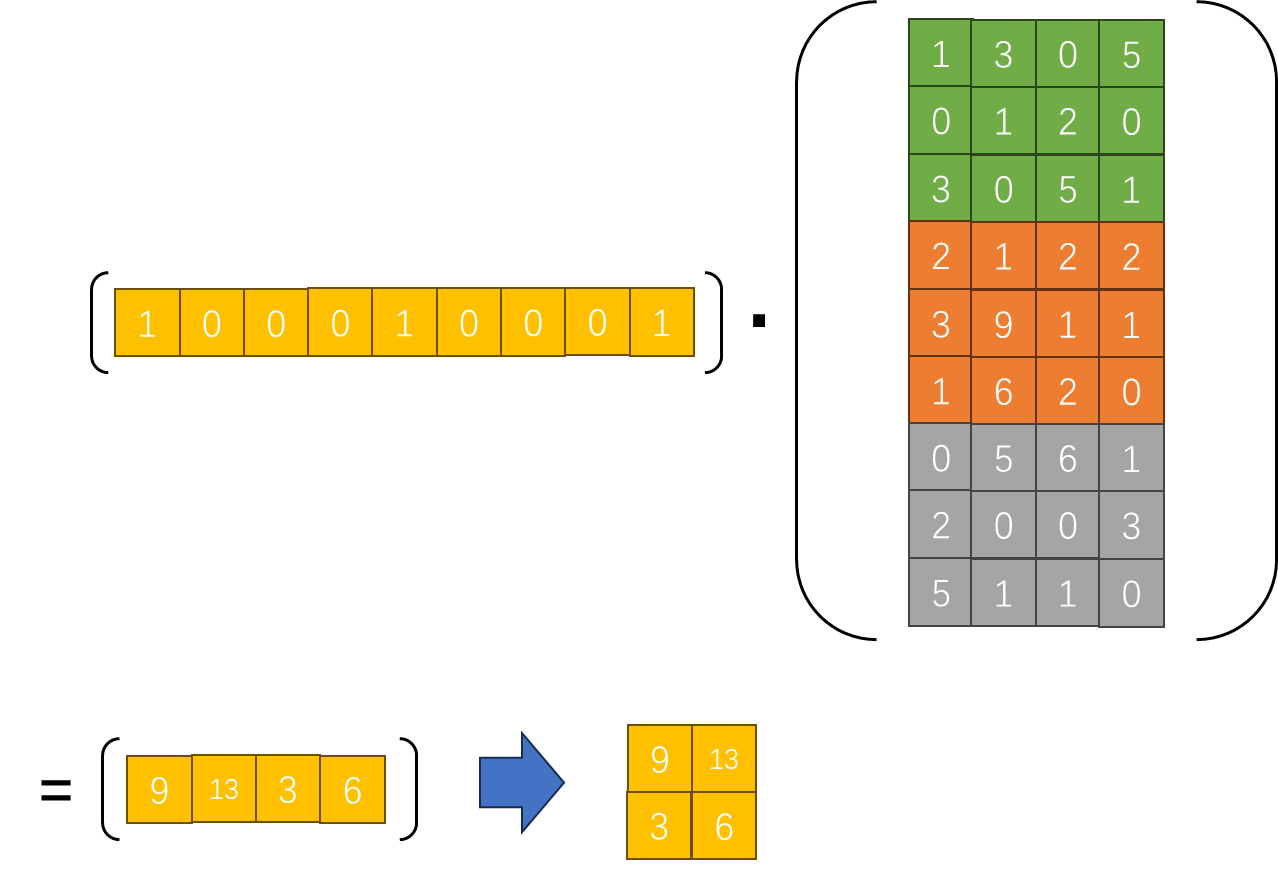矩阵乘法
- **im2col（Image to Column）**：这个步骤将输入特征图的局部区域（即卷积核每次滑动所覆盖的区域）"展平"（flatten）成一个长向量，并将所有这些向量按列组织成一个巨大的二维矩阵。简单来说，就是把输入中所有可能被卷积核"看到"的小块都拉成一列。
- 滤波器展平：将所有的卷积核（滤波器）也展平成行向量，并将它们组合成一个二维矩阵。
- 矩阵乘法：此时，卷积操作就等价于这两个大矩阵的乘法。输出的结果矩阵的每一行对应一个输出特征图的通道，每一列对应输出特征图的一个空间位置。
这种方法的优势在于，它可以充分利用高度优化的BLAS（Basic Linear Algebra Subprograms）库来执行矩阵乘法，从而在现代CPU和GPU上获得极高的计算效率。虽然它需要额外的内存来存储展平后的矩阵，但其速度优势使其成为主流实现。
总结来说 ，直接卷积是概念上的"本源"，而im2col+矩阵乘法是工程上的"加速器"。在实际的深度学习框架中，如PyTorch的torch.nn.functional.conv2d函数，其底层实现通常会根据输入尺寸、卷积核大小、硬件平台等因素，智能地选择最高效的计算路径，其中im2col+矩阵乘法是处理大规模数据时的首选方案。