AE 和 VAE 的核心差异在于编码输出的性质 和训练目标------AE 学习 "确定性编码",聚焦数据重构;VAE 学习 "概率性编码",聚焦生成建模,两者的设计逻辑和适用场景完全不同。
一、核心定义与核心目标对比
| 特性 | AE(自编码器) | VAE(变分自编码器) |
|---|---|---|
| 核心定位 | 无监督特征学习 / 数据压缩 | 生成模型(概率生成 + 特征学习) |
| 编码输出 | 确定性向量(编码后直接得到隐向量) | 概率分布(输出均值 μ 和方差 σ,隐向量从分布中采样) |
| 核心目标 | 最小化重构误差(输入≈输出) | 1. 最小化重构误差;2. 隐向量分布逼近标准正态分布 |
| 隐空间性质 | 离散、无规律(可能出现 "空洞") | 连续、平滑(全空间可采样生成) |
二、核心原理差异
1. AE:确定性重构流程
AE 的结构是 "编码器→解码器" 的简单闭环,全程无随机性:
- 编码器:输入数据(如图像、文本)通过神经网络(如 CNN、MLP),直接输出固定维度的隐向量(如 128 维),是 "输入→隐向量" 的确定性映射;
- 解码器:隐向量通过神经网络反向重构,输出与输入形状一致的数据;
- 训练目标:仅最小化重构误差(如 MSE),让解码器还原输入的细节。
关键问题
隐空间是 "离散且无序" 的 ------ 不同类别的数据可能聚集在隐空间的孤立区域,中间存在 "空洞"。若从隐空间随机采样一个向量输入解码器,重构结果会毫无意义(无法生成新数据)。
2. VAE:概率生成流程
VAE 在 AE 基础上引入 "概率建模",核心是让隐空间成为 "可采样的概率分布":
- 编码器:不直接输出隐向量,而是输出 "隐变量分布的参数"------ 均值 μ(mean)和方差 σ(log variance,避免负数值);隐向量 z 由该分布采样得到:z=μ+ε⋅σ(ε 是标准正态噪声);
- 解码器:输入采样得到的隐向量 z,重构输入数据;
- 训练目标 :双目标优化(损失 = 重构损失 + KL 散度损失):
- 重构损失:和 AE 一致,最小化输入与输出的差异;
- KL 散度损失:强制隐变量分布逼近标准正态分布(N (0,I)),让隐空间连续平滑。
关键价值
隐空间是 "连续且有规律" 的 ------ 任意采样一个标准正态分布的向量,输入解码器都能生成有意义的新数据(这是 VAE 作为 "生成模型" 的核心能力)。
三、训练损失差异
1. AE 的损失
仅包含重构损失,形式简单:
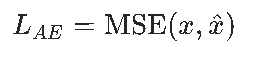
其中 x 是输入数据,x^是解码器重构输出。
2. VAE 的损失
双损失结合,平衡重构质量和生成能力:
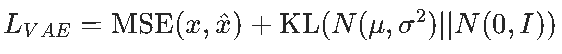
- 重构损失:保证生成数据的细节还原度;
- KL 散度损失:约束隐空间分布,避免模型 "只关注重构,忽略生成"(若不加 KL 损失,VAE 会退化为 AE)。
KL 散度的直观意义:衡量 "模型学到的隐分布" 与 "标准正态分布" 的差异,差异越小,隐空间越平滑可采样。
四、核心能力与应用场景
1. AE 的核心能力与应用
- 核心能力:特征提取、数据压缩、异常检测(如重构误差大的样本视为异常);
- 典型应用 :
- 图像去噪(输入带噪图像,输出清晰图像);
- 高维数据降维(隐向量作为低维特征);
- 异常检测(如工业产品缺陷识别、信用卡欺诈检测)。
2. VAE 的核心能力与应用
- 核心能力:概率生成(生成全新数据)、可控生成(调整隐向量改变生成结果)、特征学习;
- 典型应用 :
- 图像生成(如生成手写数字、人脸);
- 文本生成(如生成短句子);
- 数据增强(生成相似样本扩充数据集);
- 风格迁移(调整隐向量维度改变图像风格)。
五、直观示例:从隐空间采样对比
- AE:从隐空间随机选一个向量→解码器输出 "无意义的模糊数据"(因为隐空间有空洞,采样点可能落在无数据映射的区域);
- VAE:从标准正态分布随机采样一个向量→解码器输出 "有意义的新数据"(如全新的手写数字),因为隐空间是连续平滑的 "生成空间"。
总结
AE 和 VAE 的本质区别是 "是否引入概率建模":
- AE 是 "确定性重构工具",适合特征学习和数据压缩,不具备生成能力;
- VAE 是 "概率生成模型",兼顾重构与生成,核心价值是从隐空间采样生成全新数据。
选择时的核心原则:若需 "提取特征 / 异常检测",用 AE(简单高效);若需 "生成新数据 / 可控生成",用 VAE(概率建模 + 平滑隐空间)。