解码AI大模型：从神经网络到落地应用的全景探索

目录标题

解码AI大模型：从神经网络到落地应用的全景探索
- 一、神经网络：AI大模型的"思考内核"
- - [1.1 神经网络的"三层架构"：输入、隐藏与输出](#1.1 神经网络的“三层架构”：输入、隐藏与输出)
  - [1.2 正向传播：信号的"单向通行"](#1.2 正向传播：信号的“单向通行”)
  - [1.3 神经元：信号的"加工单元"](#1.3 神经元：信号的“加工单元”)
  - [1.4 激活函数：神经元的"开关与调光器"](#1.4 激活函数：神经元的“开关与调光器”)
  - 1.5常见激活函数详解
  - - [1. 阶跃函数（Step Function）：最朴素的"开关"](#1. 阶跃函数（Step Function）：最朴素的“开关”)
    - [2. Sigmoid函数：连续可调的"调光器"](#2. Sigmoid函数：连续可调的“调光器”)
    - [3. Tanh函数：零中心的"进阶调光器"](#3. Tanh函数：零中心的“进阶调光器”)
    - [4. ReLU函数：高效稳定的"单向导通器"](#4. ReLU函数：高效稳定的“单向导通器”)
    - [5. Leaky ReLU函数：解决"死亡"问题的改进版](#5. Leaky ReLU函数：解决“死亡”问题的改进版)
    - [6. GELU函数：Transformer的"标配激活函数"](#6. GELU函数：Transformer的“标配激活函数”)
    - [7. Swish函数：自适应的"动态激活器"](#7. Swish函数：自适应的“动态激活器”)
  - 1.6激活函数选型对比表
  - [1.7 权重与偏置：信号的"优先级调节器"](#1.7 权重与偏置：信号的“优先级调节器”)
  - [1.8 神经网络的参数：千亿级的"智慧密码"](#1.8 神经网络的参数：千亿级的“智慧密码”)
- 二、神经网络的学习：从"经验摸索"到"精准优化"
- - [2.1 矩阵运算：神经网络的"计算引擎"](#2.1 矩阵运算：神经网络的“计算引擎”)
  - [2.2 预测值与目标值：学习的"评价标准"](#2.2 预测值与目标值：学习的“评价标准”)
  - [2.3 损失函数：误差的"量化工具"（学习笔记）](#2.3 损失函数：误差的“量化工具”（学习笔记）)
  - [2.4 反向传播：误差的"责任分摊"](#2.4 反向传播：误差的“责任分摊”)
  - [2.5 链式求导与梯度下降：精准调参的"双引擎"](#2.5 链式求导与梯度下降：精准调参的“双引擎”)
- 三、初识大语言模型：从文字到智能的转化
- - [3.1 Token与分词：文字的"最小单元"](#3.1 Token与分词：文字的“最小单元”)
  - [3.2 词表：模型的"字典"](#3.2 词表：模型的“字典”)
  - [3.3 向量化与词嵌入：文字的"数字编码"](#3.3 向量化与词嵌入：文字的“数字编码”)
  - [3.4 大模型的输出：概率最高的"合理应答"](#3.4 大模型的输出：概率最高的“合理应答”)
  - [3.5 Softmax函数：概率的"归一化工具"（补充：归一化的其他方式+Softmax的唯一性）](#3.5 Softmax函数：概率的“归一化工具”（补充：归一化的其他方式+Softmax的唯一性）)
  - [3.6Softmax 核心公式](#3.6Softmax 核心公式)
  - 3.7两个关键特性：
  - [3.8核心适用场景和关键区分： Softmax函数 vs 损失函数](#3.8核心适用场景和关键区分： Softmax函数 vs 损失函数)
  - 3.9拓展：归一化并非只有Softmax，只是它是**概率归一化**的最优选择
  - - [3.9.1. 最值归一化（Min-Max Scaling）](#3.9.1. 最值归一化（Min-Max Scaling）)
    - [3.9. 2. 标准化（Z-Score Normalization）](#3.9. 2. 标准化（Z-Score Normalization）)
  - 3.10Softmax作为概率归一化的**不可替代性**
- 四、上下文理解：大模型的"记忆能力"
- - [4.1 循环神经网络（RNN）：串行的"记忆模式"](#4.1 循环神经网络（RNN）：串行的“记忆模式”)
  - [4.2 Transformer：并行的"上下文融合"](#4.2 Transformer：并行的“上下文融合”)
  - [4.3 稀疏自注意力：效率与效果的"平衡术"](#4.3 稀疏自注意力：效率与效果的“平衡术”)
- 五、大模型的训练：从"随机参数"到"智能模型"
- - [5.1 训练数据：模型的"知识来源"](#5.1 训练数据：模型的“知识来源”)
  - [5.2 超参数：模型的"调整旋钮"](#5.2 超参数：模型的“调整旋钮”)
  - [5.3 训练过程：批量、步长与轮次](#5.3 训练过程：批量、步长与轮次)
  - [5.4 过拟合与欠拟合：训练的"两个陷阱"](#5.4 过拟合与欠拟合：训练的“两个陷阱”)
  - [5.5 监督学习与自监督学习：训练的"两种模式"](#5.5 监督学习与自监督学习：训练的“两种模式”)
  - [5.6 温度系数与知识蒸馏：模型的"优化工具"](#5.6 温度系数与知识蒸馏：模型的“优化工具”)
- 六、AI浪潮下的基础设施：算力与网络的支撑
- - [6.1 GPU与CUDA：算力的"核心引擎"](#6.1 GPU与CUDA：算力的“核心引擎”)
  - [6.2 并行计算：算力的"规模化提升"](#6.2 并行计算：算力的“规模化提升”)
- 七、大模型的使用：从Agent到实用工具
- - [7.1 大模型的不足：知识过时与幻觉](#7.1 大模型的不足：知识过时与幻觉)
  - [7.2 Agent：大模型的"交互入口"](#7.2 Agent：大模型的“交互入口”)
  - [7.3 MCP：动态数据的"通信协议"](#7.3 MCP：动态数据的“通信协议”)
  - [7.4 RAG：消除幻觉的"外部知识库"](#7.4 RAG：消除幻觉的“外部知识库”)
  - [7.5 A2A：Agent之间的"通信标准"](#7.5 A2A：Agent之间的“通信标准”)
  - [7.6 专业技能层：Skill------AI Agent的"智能手册"（LLM的"专业导师"）](#7.6 专业技能层：Skill——AI Agent的“智能手册”（LLM的“专业导师”）)
- 八、未来的AI

解码AI大模型：从神经网络到落地应用的全景探索

人工智能并不是被"写好规则"的程序，而是一种通过数据不断逼近规律的统计系统。

大模型的强大，并非源于神秘，而是源于规模化、系统化、工程化的神经网络。

近年来，大语言模型（LLM）以前所未有的速度进入公众视野。从 ChatGPT 到 DeepSeek，从"能聊天"到"能干活"，模型的能力边界不断被刷新。但与此同时，模型参数 、Token 、Embedding 、自注意力 、RAG 、Agent 等概念，也让不少人产生了一种"看不懂但很厉害"的距离感。

事实上，大模型并不是凭空出现的黑箱系统。它的底层逻辑可以清晰拆解为三层：

数学与神经网络原理
模型架构与训练机制
工程系统与应用形态

本文将沿着这条主线，从神经网络讲起，一路拆解到 Agent 与协议化 AI，帮助你真正理解：

大模型究竟"会"在哪里，又"不会"在哪里。

一、神经网络：AI大模型的"思考内核"

提到神经网络，很多人会被微积分、矩阵运算等门槛吓退。但实际上，我们无需精通数学，也能理解其核心逻辑------它本质是对人类大脑信号传递机制的简化模拟，却构建出了强大的学习能力。

1.1 神经网络的"三层架构"：输入、隐藏与输出

神经网络之所以被称为"网络"，是因为它由多层节点互联 而成，类似计算机网络的"接入层-汇聚层-核心层"架构。

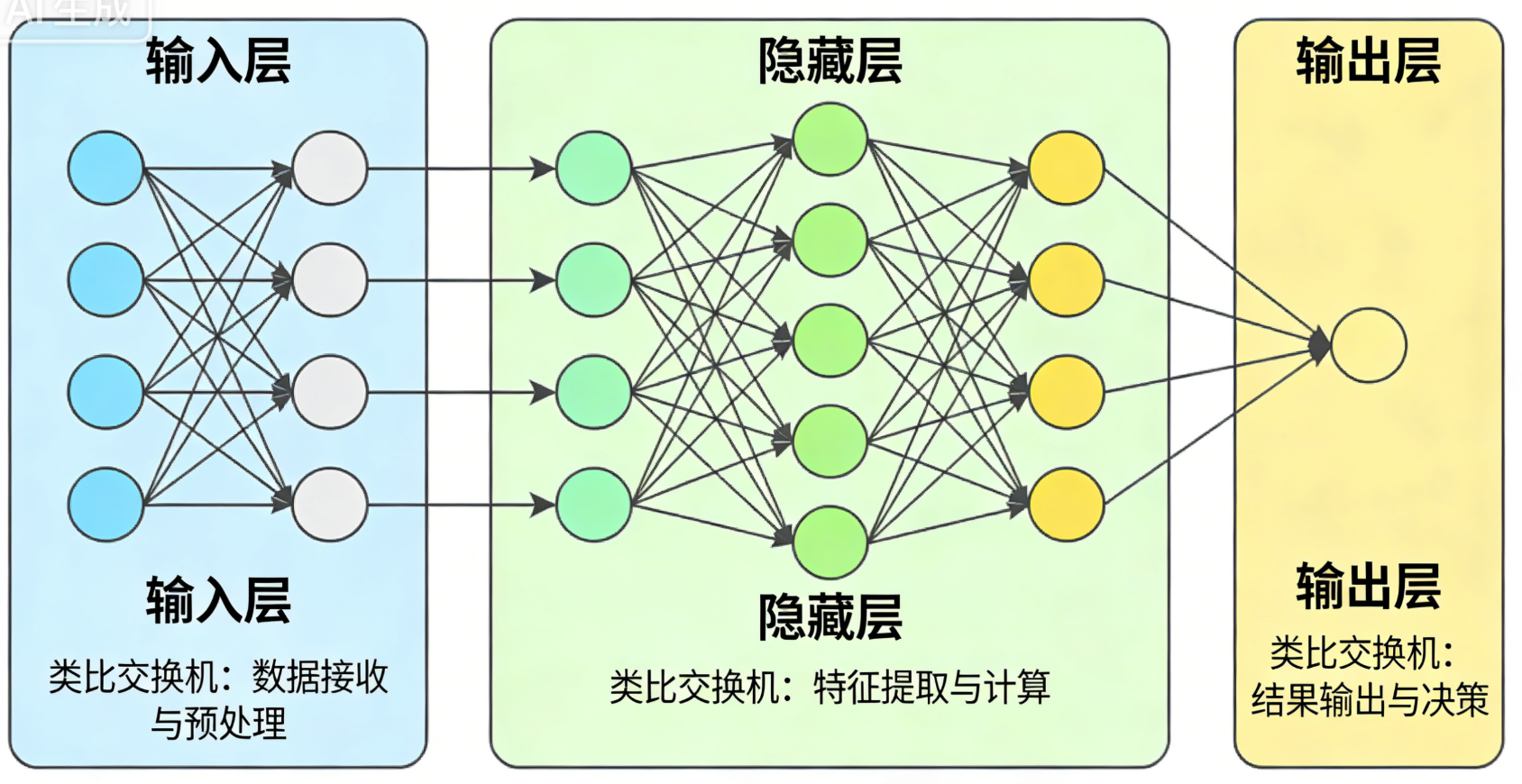
输入层（Input Layer）：接收原始数据的"信号入口"，如同计算机网络中发送数据的服务器上联的接入层交换机。比如识别图片时，输入层接收像素点数据；处理文字时，接收分词后的基础信息。
隐藏层（Hidden Layer）：位于输入层与输出层之间的"信号处理中心"，可理解为网络中的汇聚层与核心层。它的结构与输入层、输出层一致，只是因处于中间位置而得名，也被称为"黑盒层"------我们无需关注其内部细节，只需知道它在负责信号加工。
输出层（Output Layer）：输出处理结果的"信号出口"，对应接收数据的服务器上联的接入层交换机。比如识别图片后输出"猫""狗"等分类结果，处理文字后输出应答内容。

1.2 正向传播：信号的"单向通行"

与网络通信的"双工模式"不同，神经网络中的信号传递具有严格的单向性------只能从输入层经隐藏层传递到输出层，这个过程被称为"正向传播"（前馈）。

这就像家庭宽带的下行流量：短视频服务器的数据流只能通过运营商网络单向传输到家庭网络，无法反向倒流。这种单向性源于对大脑神经元的模拟------大脑中感觉神经元接收信号，经联络神经元传递，最终由运动神经元输出，整个过程不可逆。

比如当我们输入"我想吃水果"，信号会从输入层进入，逐层经过隐藏层处理，最终从输出层输出"推荐苹果、香蕉、橙子"等结果，全程不会出现信号反向传递的情况。

1.3 神经元：信号的"加工单元"

神经网络的"神经"二字，源于对大脑神经元的仿生设计。大脑神经元通过树突接收信号，经轴突传递给其他神经元，而神经网络中的每个节点就是一个"人工神经元"，具备信号接收、加工和输出的功能。

信号接收：每个神经元会接收上一层多个神经元的信号，如同树突收集来自不同神经的信息。
信号加工：神经元不会直接传递原始信号，而是对接收的信号进行"加工"------这是它与网络设备最大的区别（网络设备仅转发信号，不改变信号本身）。
信号输出：加工后的信号会传递给下一层所有神经元，如同轴突连接其他神经细胞。

大脑神经元的信号加工具有"选择性"：只有当接收的信号强度超过某个阈值时，才会输出信号，且输出强度可调节。神经网络中的神经元也模拟了这一特性，核心依赖"激活函数"实现。

1.4 激活函数：神经元的"开关与调光器"

激活函数是神经网络实现非线性处理的核心工具，它的作用是对神经元接收的信号进行非线性变换，让模型能够学习复杂的关系。

激活函数是神经网络实现非线性处理的核心工具，它的作用是对神经元接收的信号进行非线性变换，让模型能够学习复杂的关系------没有激活函数，神经网络无论叠多少层，都只是简单的线性组合，无法拟合现实世界的复杂规律。

激活函数的命名源于"激活阈值"的概念：神经元只有接收的信号超过阈值，才会被"激活"并输出信号。

1.5常见激活函数详解

1. 阶跃函数（Step Function）：最朴素的"开关"

数学表达式 ： f ( x ) = { 1 x ≥ θ 0 x < θ f(x) = \begin{cases} 1 & x \geq \theta \\ 0 & x < \theta \end{cases} f(x)={10x≥θx<θ（ θ \theta θ为阈值，通常取0）
核心特性：如同电路开关，只有"激活"和"未激活"两种状态，完美模拟早期对大脑神经元"阈值触发"的理解。
优势：计算极简单，逻辑直观，无需复杂运算。
局限性：输出仅0和1，无法表达"激活强度"；函数在阈值处不连续，无法求导，导致无法通过反向传播优化参数------这也是它逐渐被淘汰的核心原因，仅用于早期简单的感知器模型。

2. Sigmoid函数：连续可调的"调光器"

数学表达式 ： f ( x ) = 1 1 + e − x f(x) = \frac{1}{1 + e^{-x}} f(x)=1+e−x1
核心特性：输出值在(0,1)之间连续变化，能精准表达神经元的激活程度（如0.3表示弱激活，0.8表示强激活），S型曲线让信号变换更细腻。
优势：平滑连续，可导性好，适合作为输出层的激活函数（如二分类任务中输出概率）；梯度计算简单，早期在BP神经网络中广泛应用。
局限性：存在"梯度消失"问题------当x绝对值较大时（x>5或x<-5），函数导数趋近于0，导致深层网络的参数无法有效更新；输出不是零中心分布，会导致梯度更新偏向单一方向，影响训练效率。

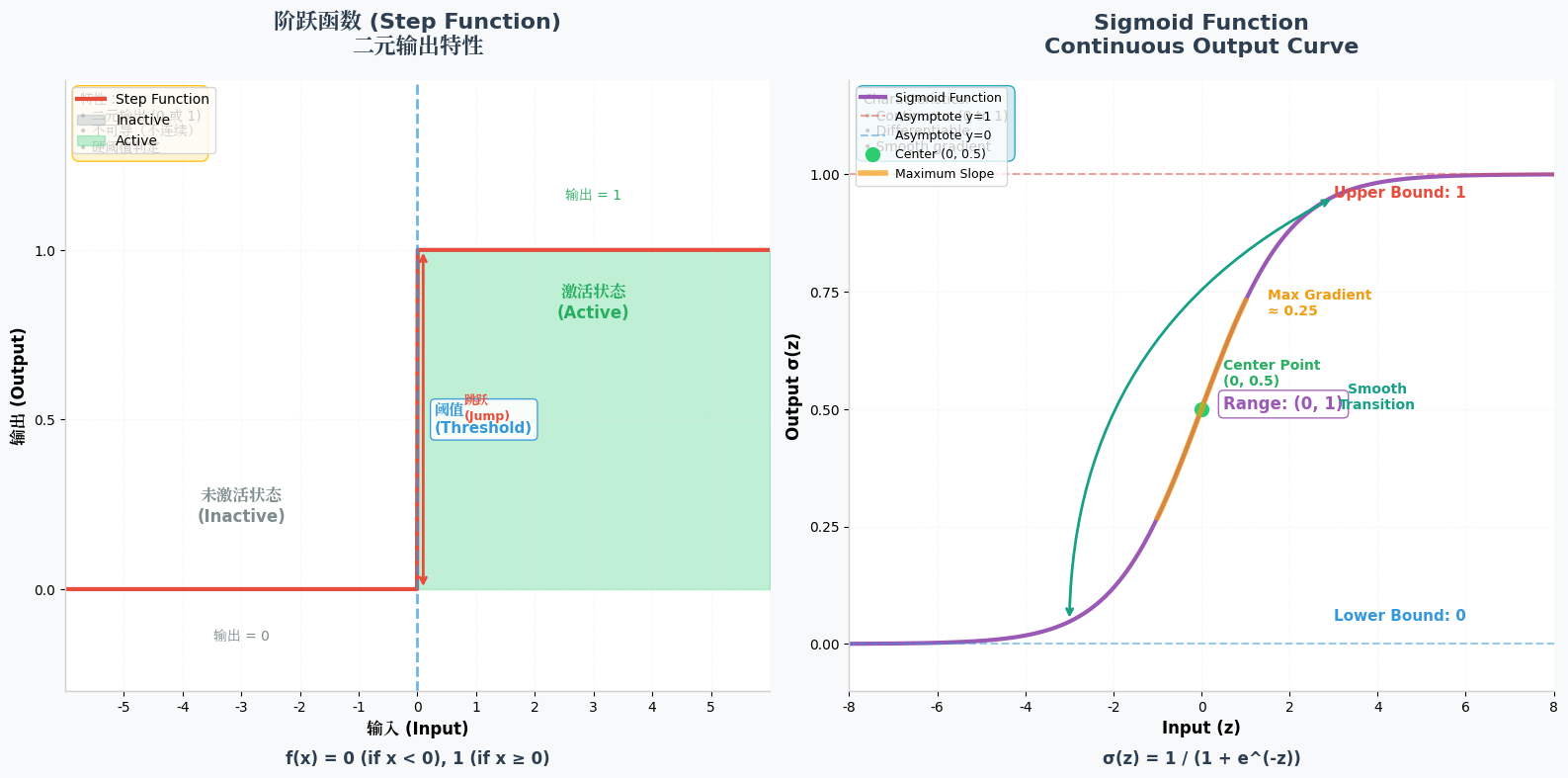
3. Tanh函数：零中心的"进阶调光器"

数学表达式 ： $f(x) = \\frac{e\^x - e^{-x}}{e^x + e\^{-x}}$ （双曲正切函数）
核心特性：输出值在(-1,1)之间连续变化，解决了Sigmoid函数"非零中心"的问题，梯度更新更稳定。
优势：零中心分布，能缓解梯度更新偏向性；相比Sigmoid，在中间区域（x∈ $-2,2$ ）梯度更大，梯度消失问题有所改善。
局限性：仍未完全解决梯度消失问题------当x绝对值过大时，导数依然趋近于0；计算量比Sigmoid略大（需计算指数差）。
适用场景：常用于深层神经网络的隐藏层，尤其在循环神经网络（RNN）早期版本中应用较多。

4. ReLU函数：高效稳定的"单向导通器"

数学表达式：( f(x) = \max(0, x) )（修正线性单元）
核心特性：x≥0时直接输出x（线性传递），x<0时输出0（完全抑制），类似"单向导通"的电子元件。
优势：计算极高效（仅需判断大小），GPU并行计算友好；有效缓解梯度消失问题------x>0时导数恒为1，深层网络的梯度能有效传递；稀疏激活特性（大量负输入被抑制），减少模型冗余计算，提升泛化能力。
局限性：存在"死亡ReLU"问题------当训练过程中神经元长期接收负输入，输出恒为0，梯度无法更新，该神经元永久"失效"；输出仍非零中心分布。
适用场景：目前深度学习中最常用的激活函数，广泛应用于CNN、Transformer等模型的隐藏层，是工业界的"首选方案"。

5. Leaky ReLU函数：解决"死亡"问题的改进版

数学表达式 ： f ( x ) = { x x ≥ 0 α x x < 0 f(x) = \begin{cases} x & x \geq 0 \\ \alpha x & x < 0 \end{cases} f(x)={xαxx≥0x<0 （ α \alpha α 为小于1的正数，通常取0.01）
核心特性 ：在ReLU基础上，为负输入保留微小的梯度（ α x \alpha x αx），避免神经元永久"死亡"。
优势：继承ReLU的高效性和梯度传递能力；解决"死亡ReLU"问题，负输入区域仍能更新参数。
局限性 ： α \alpha α 是手动设置的超参数，需通过验证集调优，缺乏自适应调整机制；实际效果不稳定，部分场景下性能不如ReLU。

6. GELU函数：Transformer的"标配激活函数"

数学表达式 ： f ( x ) = x ⋅ Φ ( x ) f(x) = x \cdot \Phi(x) f(x)=x⋅Φ(x)（ P h i ( x ) Phi(x) Phi(x)为标准正态分布的累积分布函数，近似表达式为 f ( x ) = 0.5 x ( 1 + tanh ⁡ ( 2 / π ( x + 0.044715 x 3 ) ) ) f(x) = 0.5x(1 + \tanh(\sqrt{2/\pi}(x + 0.044715x^3))) f(x)=0.5x(1+tanh(2/π (x+0.044715x3)))）
核心特性：融合了ReLU的稀疏激活和Sigmoid的平滑特性，输出更接近自然数据的分布，对噪声更鲁棒。
优势：梯度特性优异，无梯度消失问题；适配Transformer的多头注意力机制，能更好地捕捉文本、图像等数据的复杂语义关联；计算效率与ReLU相当。
局限性：近似表达式的计算量略大于ReLU；仅在深层模型（如Transformer、大语言模型）中优势明显，简单模型中性价比不如ReLU。
适用场景：目前主流大模型（如GPT、BERT、DeepSeek）的默认激活函数，是Transformer架构的"核心组件"之一。

7. Swish函数：自适应的"动态激活器"

数学表达式 ： f ( x ) = x ⋅ σ ( x ) f(x) = x \cdot \sigma(x) f(x)=x⋅σ(x)（ σ ( x ) \sigma(x) σ(x) 为Sigmoid函数）
核心特性：将输入x与Sigmoid的输出相乘，形成"自门控"机制------Sigmoid输出动态调节x的传递强度，自适应不同输入的激活需求。
优势：非线性表达能力强，能拟合更复杂的函数关系；在深层网络中表现优于ReLU，部分场景下能提升模型精度。
局限性：计算量较大（需同时计算Sigmoid和乘法）；x绝对值较大时仍存在轻微的梯度衰减问题；稳定性不如ReLU和GELU，未成为主流选择。

1.6激活函数选型对比表

激活函数	输出范围	核心优势	主要缺陷	典型应用场景
阶跃函数	{0,1}	计算极简，逻辑直观	不连续、不可导	早期感知器模型
Sigmoid	(0,1)	输出概率化，可导性好	梯度消失、非零中心	二分类任务输出层
Tanh	(-1,1)	零中心分布，梯度更稳	梯度消失	RNN隐藏层（早期）
ReLU	[0,+∞)	高效、抗梯度消失	死亡ReLU、非零中心	CNN/Transformer隐藏层
Leaky ReLU	(-∞,+∞)	解决死亡ReLU问题	α需手动调优	替代ReLU的备选方案
GELU	(-∞,+∞)	适配Transformer，鲁棒性强	近似计算略复杂	大语言模型、Transformer
Swish	(-∞,+∞)	自适应门控，表达能力强	计算量大、稳定性一般	深层模型实验性应用

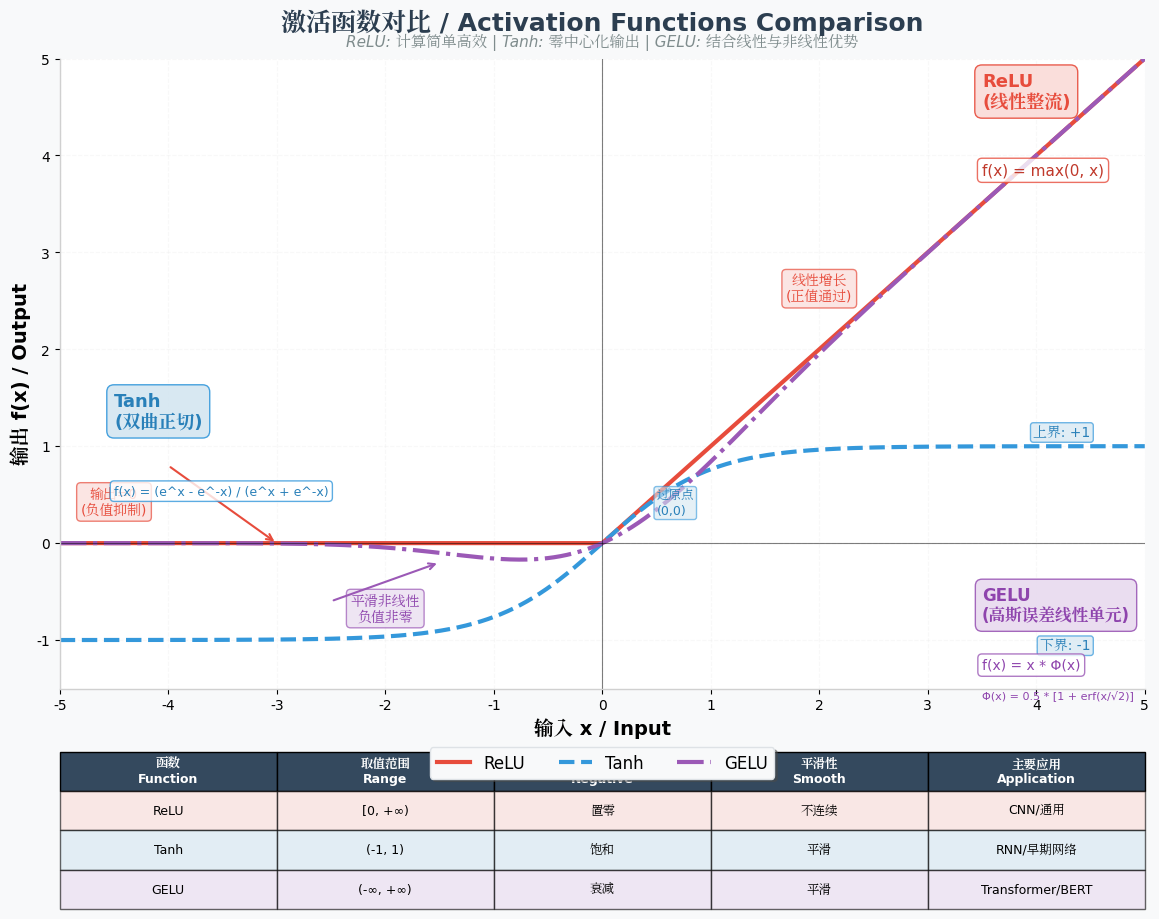
选型核心原则

优先选GELU：若使用Transformer架构或大语言模型，GELU是最优选择，适配模型的并行计算和语义捕捉需求。
默认选ReLU：普通深层网络（如CNN、简单DNN）中，ReLU的"高效性+抗梯度消失"优势突出，是性价比最高的选择。
输出层按需选：二分类任务用Sigmoid（输出概率），多分类任务用Softmax（后续章节详解），回归任务可直接不用激活函数（或用ReLU）。
避免阶跃函数：仅用于理论学习，实际工程中已完全淘汰。
缓解死亡ReLU：若训练中发现模型收敛缓慢，可尝试Leaky ReLU（α=0.01）或GELU替代ReLU。

1.7 权重与偏置：信号的"优先级调节器"

输入层神经元会将信号传递给隐藏层所有神经元，隐藏层神经元需要对多个输入信号进行"综合处理"------这个过程依赖"权重"和"偏置"两个核心参数。

权重（Weight）：表示每个输入信号的重要程度，如同给不同的网络方案分配不同的优先级。比如输入"我想吃甜的水果"，"甜"这个信号的权重会高于其他信号，让模型优先推荐苹果、香蕉等甜水果。
偏置（Bias）：调节神经元的激活难度，相当于给激活阈值"加减分"。偏置为正时，神经元更容易被激活；偏置为负时，神经元更难被激活。

神经元的信号处理公式为：y = f(wx + b)，其中：

y是输出信号，f是激活函数，w是权重，x是输入信号，b是偏置。
先通过wx + b对输入信号进行线性组合（加权求和），再通过激活函数f进行非线性变换，最终输出处理后的信号。

1.8 神经网络的参数：千亿级的"智慧密码"

权重和偏置是神经网络的核心参数，模型的"智慧"就蕴含在这些参数之中。随着隐藏层数量增加（形成深度神经网络）和每层节点增多，参数规模会呈指数级增长：

GPT-3的参数规模达1750亿；
Deepseek V3.2的参数规模已突破6700亿。

这些参数并非"变量"，而是"可优化的常量"：

训练阶段：参数会随着数据迭代不断调整，直至模型性能达标；
训练结束：参数会固定下来，成为模型的"固有属性"（重新训练需修改千亿级参数，成本极高）；
推理阶段：模型接收的输入数据才是真正的"变量"，这些数据会被转换为数字形式供模型计算。

模型文件的主体就是这些参数，再加上一个"词表"------神经网络输出的数值会通过词表映射为人类可读的文字，比如将数值"0.98"映射为"苹果"。

二、神经网络的学习：从"经验摸索"到"精准优化"

神经网络的强大之处在于它能通过"学习"不断优化参数，提升处理能力。这个过程类似人类从实践中积累经验，核心是通过"误差反馈"调整参数，让输出结果越来越接近目标。

2.1 矩阵运算：神经网络的"计算引擎"

神经网络的正向传播本质是一系列矩阵运算。对于拥有千亿级参数的深度神经网络，逐神经元分步计算效率极低，而矩阵运算能将复杂的计算过程简化为批量运算，再通过GPU实现并行计算。

比如一个输入层有2个神经元、隐藏层有2个神经元、输出层有2个神经元的简单网络：

先将隐藏层的权重整理为2×2的矩阵；
把输入信号整理为2×1的列向量；
一次矩阵乘法就能算出隐藏层所有神经元的加权和；
经激活函数变换后，再通过矩阵运算传递到输出层。

这种计算方式让神经网络能够高效处理海量数据，为大模型的规模化应用奠定了基础。

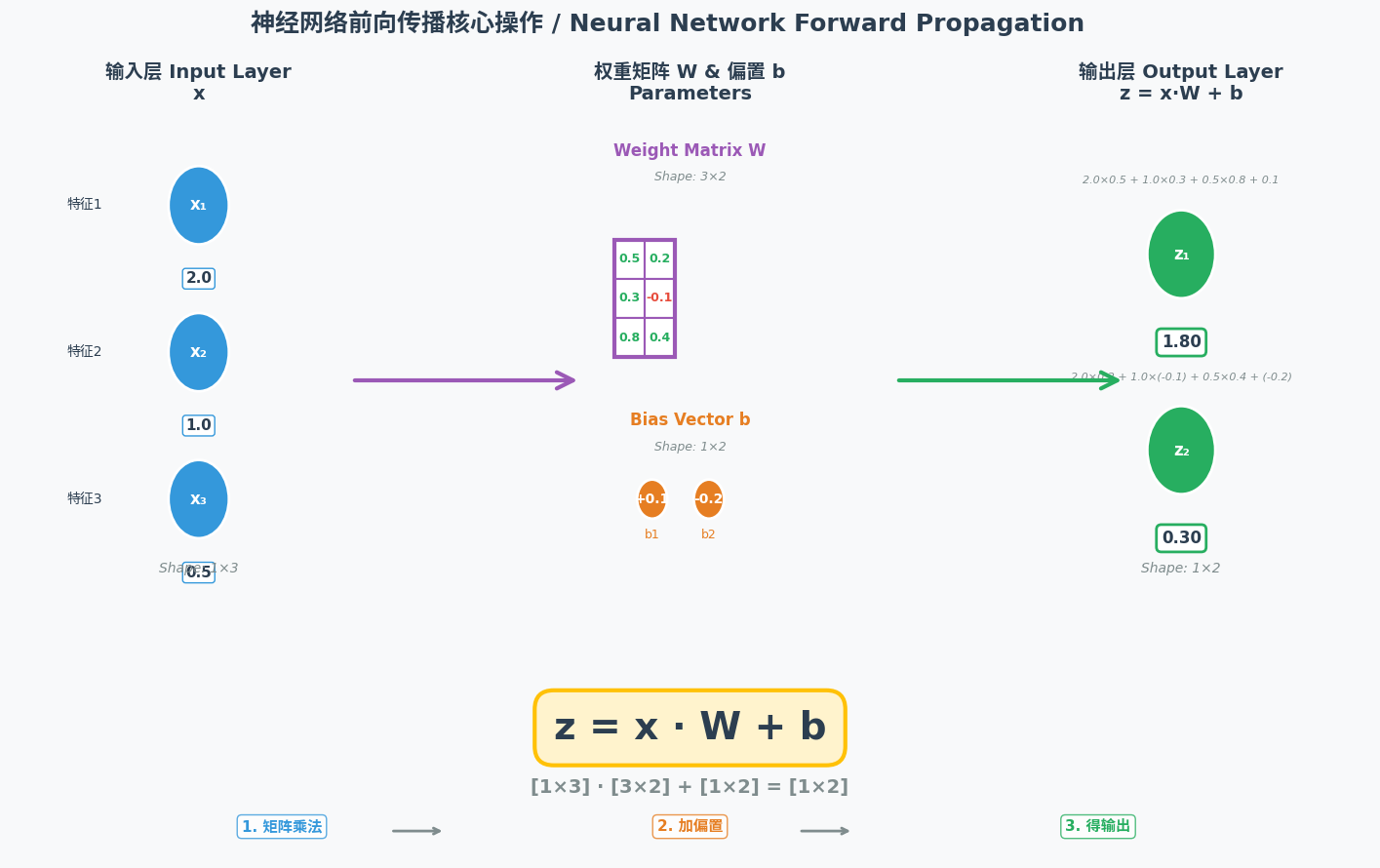
2.2 预测值与目标值：学习的"评价标准"

神经网络的输出称为"预测值"，而我们期望的理想结果称为"目标值"。学习的核心就是缩小预测值与目标值的差距：

若输入"恭喜"，目标值是"发财"，而模型输出"春节"，则说明预测值与目标值差距较大，需要调整参数；
若模型输出"发财"，则说明预测值接近目标值，参数无需大幅调整。

标注目标值的过程称为"打标签"，比如给猫的图片打上"猫"的标签，给"恭喜"搭配"发财"的标签。

2.3 损失函数：误差的"量化工具"（学习笔记）

预测值与目标值之间的偏差被称为误差（也叫损失），但原始的偏差直接相加减会出现正负抵消的问题，无法真实反映模型的整体预测误差。损失函数的核心作用，就是通过特定的数学运算对所有样本的预测偏差做量化整合，既消除正负误差的抵消问题，又能让模型清晰感知自身的预测不足，成为模型优化的"核心评判标准"。

简单来说，损失函数是模型的"成绩单"：损失值越小，代表模型的预测结果越贴近真实的目标值，模型的性能越好；反之则说明模型预测偏差大，需要进一步调整优化。

不同的任务场景（回归、分类、生成/语言建模等）适配不同的损失函数，核心是让损失的计算方式贴合任务的本质需求，以下是三类最常用的损失函数：

绝对值损失（L1损失）

核心计算：对单个样本的预测误差直接取绝对值，公式为 L = ∣ y − y ^ ∣ L=|y-\hat{y}| L=∣y−y^∣（其中 y y y 为真实目标值， y ^ \hat{y} y^ 为模型预测值）。
核心特点：通过取绝对值简单消除误差的负号，计算难度低、对异常值的鲁棒性强（不会过度放大极端偏差）；但存在明显缺陷------在误差为0处的导数不连续，可能会减慢模型的优化速度，影响收敛效率。
适用场景：简单回归任务（如简单数值预测），或对异常值敏感、不希望极端偏差过度影响模型的预测场景。

平方损失（L2损失/均方误差MSE）

核心计算：对单个样本的预测误差做平方运算，实际应用中常用"均方误差"（所有样本损失值的平均值），公式为 M S E = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 MSE=\frac{1}{n}\sum_{i=1}^n(y_i-\hat{y}_i)^2 MSE=n1∑i=1n(yi−y^i)2（其中 n n n 为样本总数， y i y_i yi 为第 i i i个样本的真实值， y ^ i \hat{y}_i y^i 为第 i i i个样本的预测值）。
核心特点：平方运算会放大较大的误差，让模型对明显的预测错误更敏感，会优先修正偏差大的样本；同时函数光滑可导，能让模型的优化过程更平稳、收敛更高效。缺点是对异常值的鲁棒性差，极端偏差会被平方大幅放大，主导整体损失值，进而影响模型的优化方向。
适用场景：大部分经典回归任务（如房价预测、销量预测、气温预测），是回归任务中最常用的默认损失函数。

交叉熵损失

核心计算：基于信息论的熵值概念设计，核心是计算模型预测的概率分布与真实的概率分布之间的差异，常用公式为 L = − ∑ i = 1 n y i log ⁡ ( y ^ i ) L=-\sum_{i=1}^n y_i \log(\hat{y}_i) L=−∑i=1nyilog(y^i)（其中 y i y_i yi为真实标签的概率分布， y ^ i \hat{y}_i y^i为模型预测的概率分布， n n n为类别总数），差异越小则损失值越低，完美适配概率类模型的误差衡量。
核心特点：能精准衡量模型对各类别/结果的预测置信度与真实情况的偏差；在分类任务中，会让模型优先修正"预测置信度与真实结果偏差大"的样本，优化针对性更强；无需复杂转换，可直接适配概率输出类模型。
适用场景：分类任务（如图片识别、垃圾邮件检测、文本分类）的核心损失函数；同时也是大语言模型、生成式AI的核心损失函数------因为语言模型的本质是概率模型，其输出是对下一个token/语句的概率分布预测，交叉熵能完美匹配这一特性，精准衡量语言生成的合理性与准确性。

机器学习/深度学习的核心学习逻辑，就是以损失函数为目标，通过优化算法（如梯度下降）不断调整模型的参数，让损失函数的计算结果无限逼近0。当损失值趋近于0时，代表模型的预测值与真实目标值几乎完全一致，模型的预测能力达到最优。

简单来说，损失函数为模型指明了"优化方向"：模型通过计算损失值，能清晰知道自己"预测错了多少、错在哪里"；而优化算法则根据损失值的变化趋势，指导模型"该调整哪些参数、调整多少幅度"，形成"计算损失→调整参数→再计算损失"的循环，直至模型性能达到最优。

2.4 反向传播：误差的"责任分摊"

由于神经网络的输出是所有神经元共同作用的结果，当出现误差时，需要将误差逐层分摊到每个神经元，让它们各自调整参数------这个过程就是"反向传播"。

反向传播的逻辑类似工厂的"责任追溯"：成品检测不合格时，会从最终工序反向追溯，找出每个环节的问题。在神经网络中：

误差从输出层开始，逐层向输入层传递；
每个神经元根据自身的权重大小承担相应的误差（权重越大，责任越大）；
神经元根据分摊的误差调整自身的权重和偏置，减少后续误差。

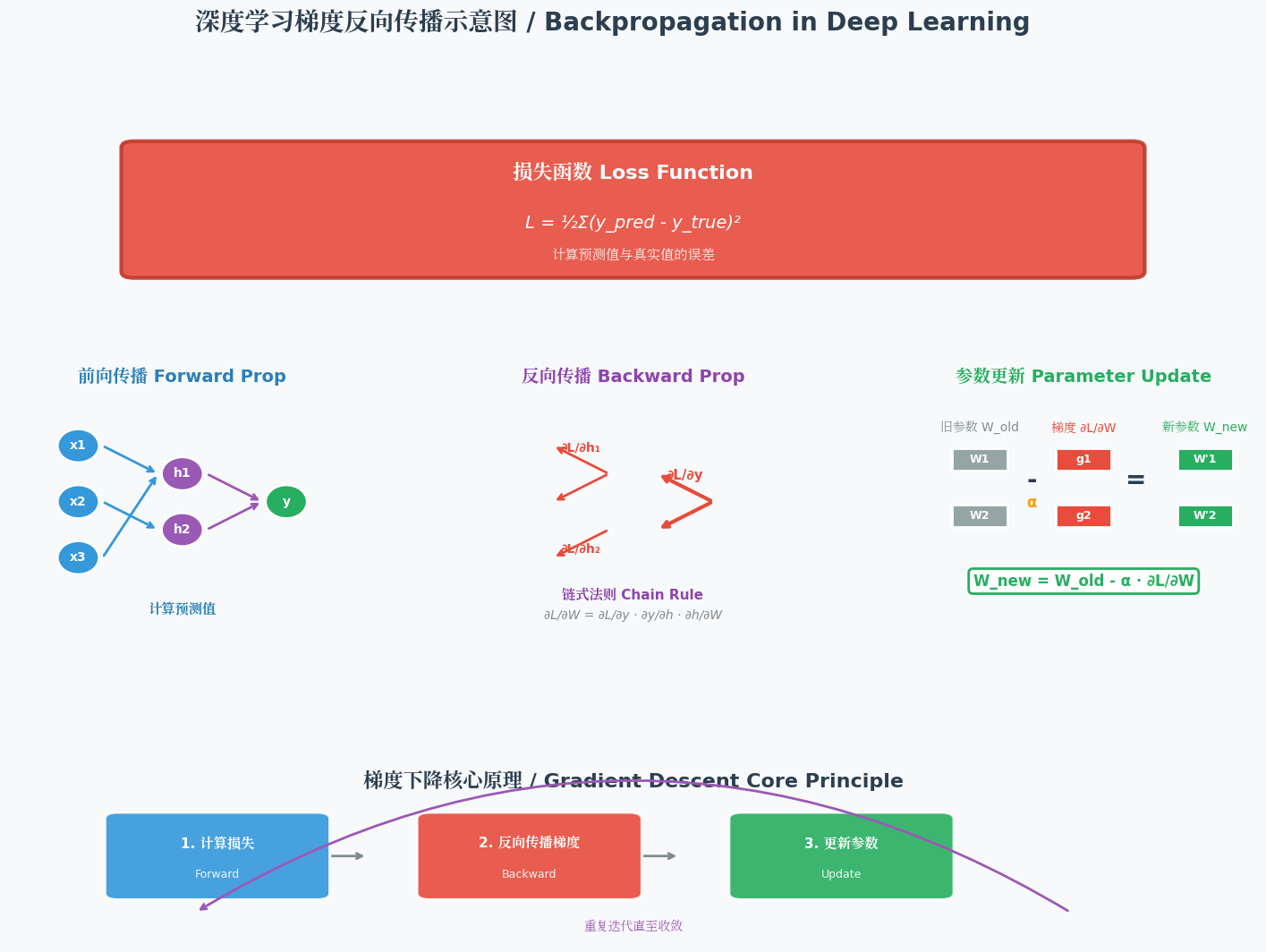
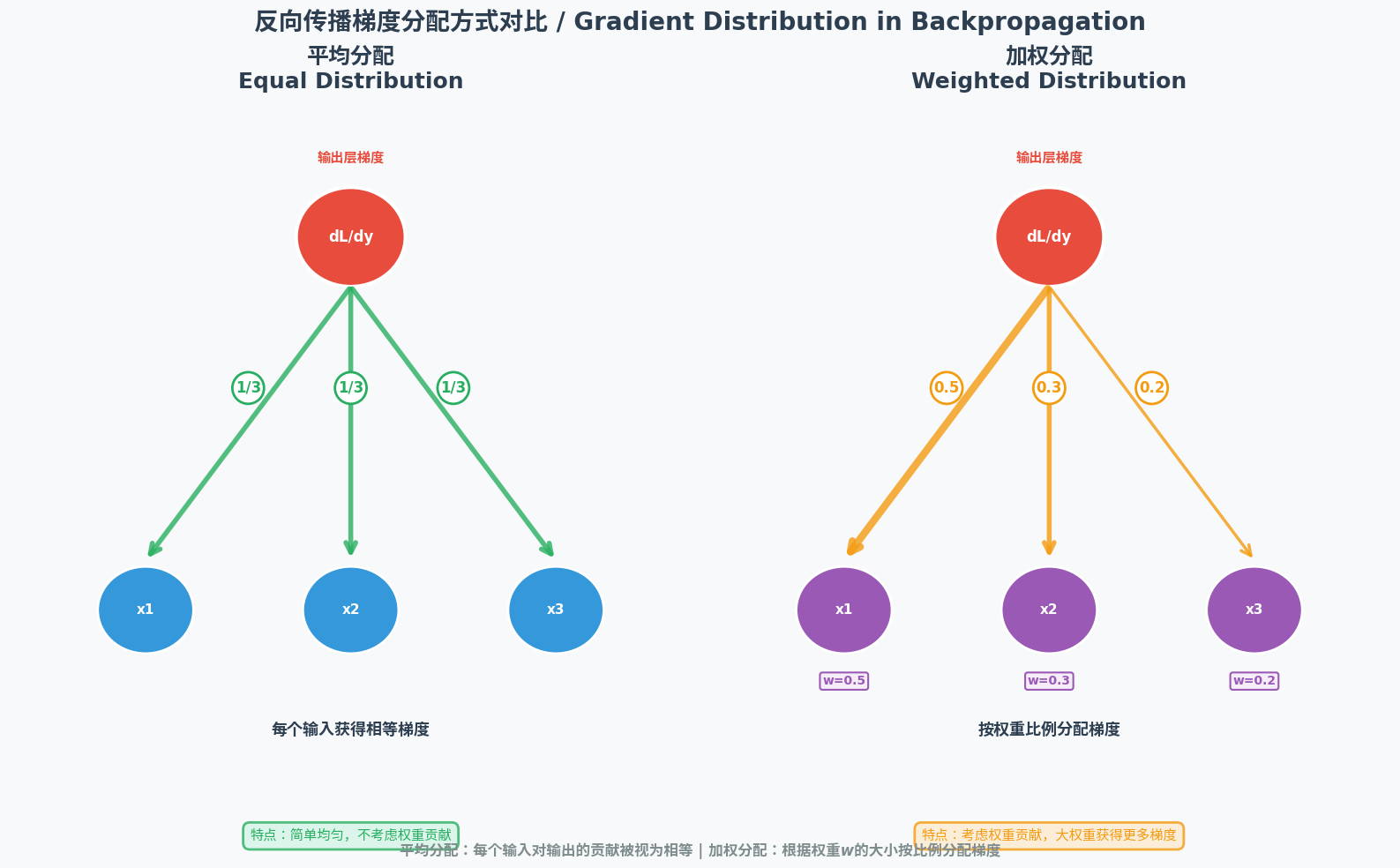
2.5 链式求导与梯度下降：精准调参的"双引擎"

早期神经网络的参数调整全靠"经验摸索"，如同和面时凭感觉加水加面，效率极低。1986年辛顿等人提出的"链式求导法则"，为参数调整提供了精准的数学依据。

链式求导：如同多米诺骨牌，从最外层的损失函数向最内层的输入信号逐层计算偏导数，精准确定每个参数对误差的影响程度。它要求损失函数和激活函数必须连续（比如Sigmoid函数），这也是阶跃函数被淘汰的重要原因。
梯度下降：链式求导计算出的偏导数构成"梯度"，它像一个"指南针"，指示参数调整的方向。梯度下降法按照这个方向逐步调整参数，让损失函数的结果持续下降，最终达到最小值。

这就像登山者寻找下山的最短路径：梯度指示了坡度最陡的方向，沿着这个方向小步前进，就能最快到达山脚（误差最小）。

三、初识大语言模型：从文字到智能的转化

神经网络是大语言模型的"骨架"，而大语言模型是神经网络在自然语言处理领域的专项应用。它的核心逻辑是将文字转换为数字，通过神经网络计算后，再将数字转换为人类可读的文字。

3.1 Token与分词：文字的"最小单元"

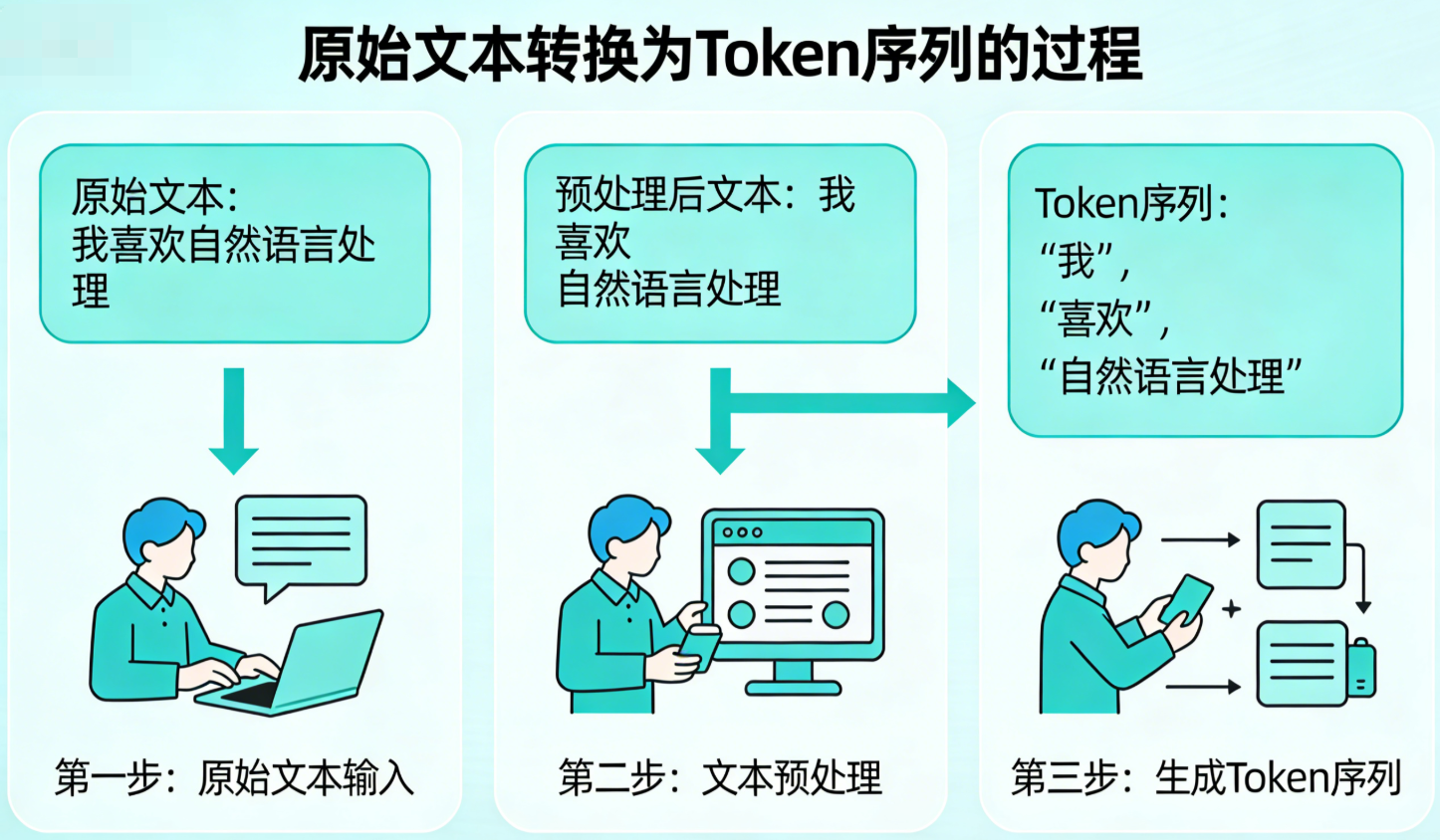
大语言模型处理文字时，首先要将文本拆解为语义紧密的最小单元，这个过程称为"分词"，拆分后的单元称为"Token"。

分词的核心是"语义完整性"：比如"我爱吃香蕉"会被拆分为"我|爱|吃|香蕉"，而"香蕉"不会被拆分为"香|蕉"------因为"香蕉"是一个完整的语义单元。

常用的分词算法是BPE（字节对编码）：如果两个字在文本中频繁同时出现（高概率相邻），就会被组合为一个Token，加入分词表。比如"人工智能"在文本中频繁同时出现，就会被当作一个Token，而不是拆分为"人|工|智|能"。

图示说明：以"我喜欢自然语言处理"为例，展示分词前后的对比。

3.2 词表：模型的"字典"

所有预先生成的Token会被记录在"词表"中，模型训练和推理时，都需要通过查询词表来分词。词表的大小需要平衡：

词表过大：若训练数据不足，部分Token无法被充分学习，导致模型理解能力不足；
词表过小：如同用一年级生词本理解长篇小说，模型的表达和理解能力会受限。

模型的理解能力完全取决于对词表中Token语义的掌握，因此训练数据的质量至关重要------高质量的语料能让模型更好地理解每个Token的含义和用法。

3.3 向量化与词嵌入：文字的"数字编码"

神经网络的计算对象是数字，因此Token需要被转换为数字形式，这个过程称为"向量化"。由于单个数字的表达能力有限，模型通常采用"多维向量"（张量）表示Token，这个过程也被称为"词嵌入（Word Embedding）"。

多维向量的核心作用是表达语义关联：

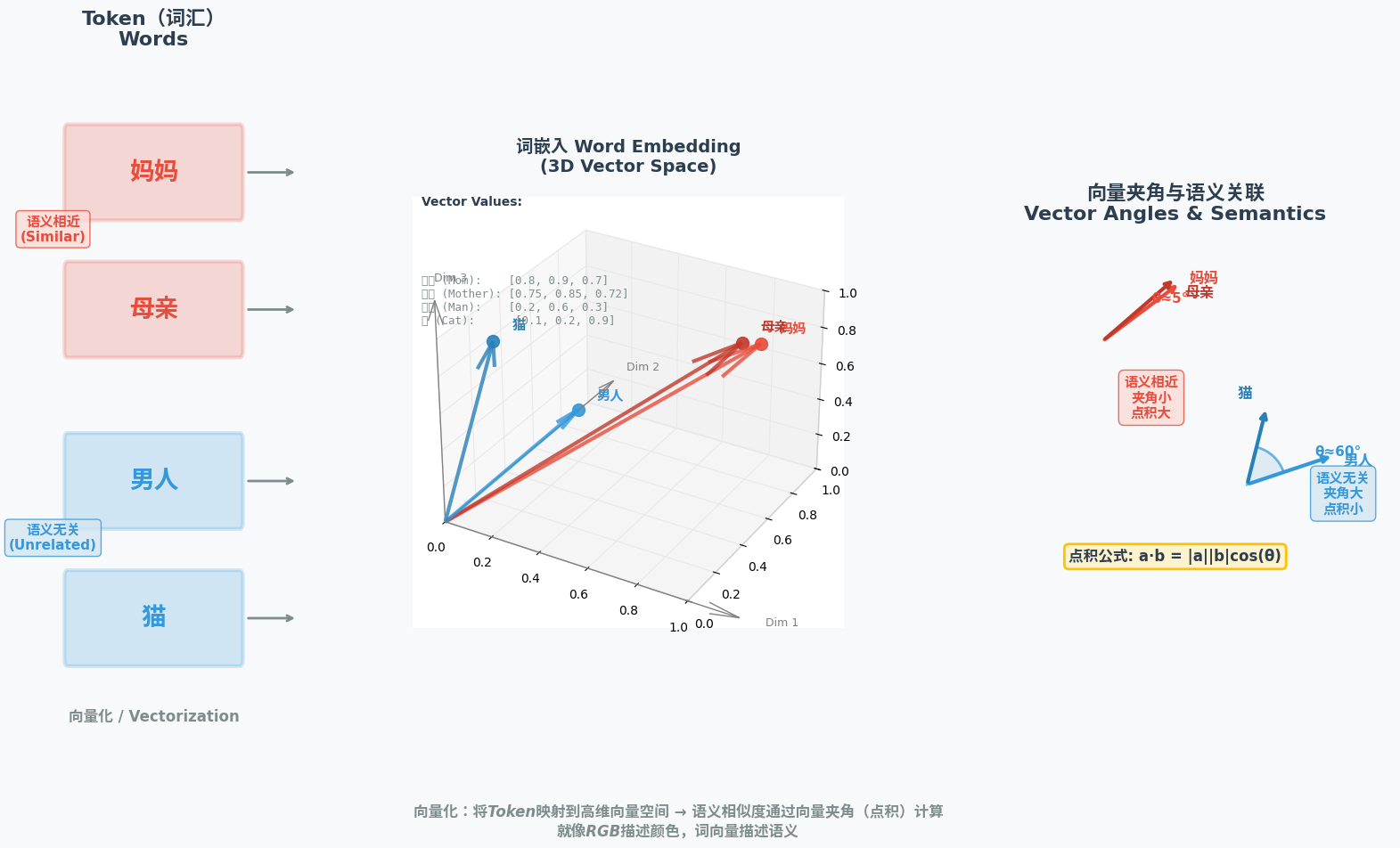
语义相近的Token，向量夹角越小（通过向量点积计算），比如"妈妈"和"母亲"的向量夹角接近0；
语义无关的Token，向量夹角越大，比如"男人"和"猫"的向量夹角较大。

这就像用RGB三原色描述颜色：每种颜色都可以用一个三维向量表示，向量的差异对应颜色的不同；而每个Token的向量差异，对应语义的不同。

图示说明：左侧为Token（中文标注"妈妈""母亲""男人""猫"），中间为对应的多维向量（英文标注向量数值），右侧为向量夹角示意图（中文标注"语义相近""语义无关"）。

3.4 大模型的输出：概率最高的"合理应答"

大语言模型本质是"概率预测模型"，它的输出是词表中所有Token的预测概率------模型会选择概率最高的Token作为最终输出。

比如输入"恭喜"，模型会计算词表中所有Token的概率：

"发财"的概率0.6；
"新婚快乐"的概率0.15；
"喜得贵子"的概率0.15；
"夺冠"的概率0.1；
其他Token的概率接近0。

最终模型会输出"发财"，因为它的概率最高。这种概率预测源于训练数据中的语料分布------训练数据中"恭喜"与"发财"同时出现的频率最高，模型就会认为二者的关联性最强。

3.5 Softmax函数：概率的"归一化工具"（补充：归一化的其他方式+Softmax的唯一性）

神经网络的原始输出是一组无约束的连续数值（也叫logits ），这类数值既无固定范围，总和也不等于1，无法直接表示各类别的发生概率。Softmax函数的核心作用，就是对这组原始输出做概率化归一化处理 ，将其转换为总和严格为1的概率分布，同时保留原始数值间的相对大小关系，实现概率的"此消彼长"。

3.6Softmax 核心公式

1.Softmax 简单公式

设神经网络最后一层的原始输出（logits） 为一维向量 z = $z 1 , z 2 , . . . , z n$ z = $z_1, z_2, ..., z_n$ z= $z1,z2,...,zn$ ，其中 n n n 为分类类别数，经过 Softmax 激活后，每个类别对应的概率 a i a_i ai 公式为：
a i = e z i ∑ j = 1 n e z j ( i = 1 , 2 , . . . , n ) \boldsymbol{a_i = \frac{e^{z_i}}{\sum_{j=1}^n e^{z_j}} \quad (i=1,2,...,n)} ai=∑j=1nezjezi(i=1,2,...,n)
关键特性 ：所有类别概率之和为 1，即 ∑ i = 1 n a i = 1 \sum_{i=1}^n a_i = 1 ∑i=1nai=1，满足概率分布的基本要求。
2.数值稳定版 Softmax 公式（工程必用）

原始公式中，若 z i z_i zi 数值过大， e z i e^{z_i} ezi 会发生指数爆炸 导致浮点数溢出，因此工程实现时会先对所有 z i z_i zi 减去向量中的最大值 z m a x = max ⁡ ( z 1 , z 2 , . . . , z n ) z_{max} = \max(z_1,z_2,...,z_n) zmax=max(z1,z2,...,zn)，推导后公式不变且能避免溢出：
a i = e z i − z m a x ∑ j = 1 n e z j − z m a x \boldsymbol{a_i = \frac{e^{z_i - z_{max}}}{\sum_{j=1}^n e^{z_j - z_{max}}}} ai=∑j=1nezj−zmaxezi−zmax
推导依据 ：分子分母同乘 e − z m a x e^{-z_{max}} e−zmax（非零常数），分式值不变，即
e z i ∑ j e z j = e z i ⋅ e − z m a x ∑ j e z j ⋅ e − z m a x = e z i − z m a x ∑ j e z j − z m a x \frac{e^{z_i}}{ \sum_j e^{z_j} } = \frac{e^{z_i} \cdot e^{-z_{max}} }{ \sum_j e^{z_j} \cdot e^{-z_{max}} } = \frac{e^{z_i - z_{max}} }{ \sum_j e^{z_j - z_{max}} } ∑jezjezi=∑jezj⋅e−zmaxezi⋅e−zmax=∑jezj−zmaxezi−zmax

公式关键说明

e x e^x ex：自然指数函数；

z m a x z_{max} zmax：对原始得分向量取最大值（解决指数爆炸问题，工程必用）；

所有类别概率之和 ∑ i = 1 k a i = 1 \sum_{i=1}^k a_i = 1 ∑i=1kai=1（满足概率分布）。

3.简化示例（二分类场景）

当 n = 2 n=2 n=2（二分类），Softmax 退化为和 Sigmoid 等价的形式，验证如下：

设 z = $z 1 , z 2$ z= $z_1, z_2$ z= $z1,z2$ ，则
a 1 = e z 1 e z 1 + e z 2 , a 2 = e z 2 e z 1 + e z 2 = 1 − a 1 a_1 = \frac{e^{z_1}}{e^{z_1}+e^{z_2}}, \quad a_2 = \frac{e^{z_2}}{e^{z_1}+e^{z_2}} = 1 - a_1 a1=ez1+ez2ez1,a2=ez1+ez2ez2=1−a1

若令 z 1 = x , z 2 = 0 z_1 = x, z_2 = 0 z1=x,z2=0（二分类常将其中一类输出置0），则 a 1 = e x e x + 1 a_1 = \frac{e^x}{e^x+1} a1=ex+1ex，即为Sigmoid 公式。
4.Softmax 梯度公式（与交叉熵搭配，损失对 logits 的梯度）

实际训练中，Softmax 必与交叉熵损失（Cross-Entropy） 搭配，可简化梯度计算（避免单独求 Softmax 梯度的复杂链式法则）。

设真实标签为独热向量 y = $y 1 , y 2 , . . . , y n$ y = $y_1,y_2,...,y_n$ y= $y1,y2,...,yn$ （仅目标类别为 1，其余为 0），损失函数 L = − ∑ i = 1 n y i ln ⁡ a i L = -\sum_{i=1}^n y_i \ln a_i L=−∑i=1nyilnai，则损失对原始输出 z i z_i zi 的梯度 为：
∂ L ∂ z i = a i − y i \boldsymbol{\frac{\partial L}{\partial z_i} = a_i - y_i} ∂zi∂L=ai−yi
核心优势：梯度结果极简，仅为「Softmax 输出概率 - 真实标签」，大幅降低训练计算量。

3.7两个关键特性：

保序性：原始输出中数值越大的维度，转换后的概率值越高；数值越小的维度，概率值越低，相对大小关系完全不变；
排他性：所有维度的概率总和为1，一个维度的概率升高，必然伴随其他维度的概率降低，贴合分类任务中"类别互斥"的概率表达需求。

直观示例 ：

若神经网络针对某一分类任务的原始输出为 $2.5 , 0.6 , 0.1 , 1.8$ $2.5, 0.6, 0.1, 1.8$ $2.5,0.6,0.1,1.8$ ，经Softmax函数处理后，会转换为概率分布 $0.6 , 0.15 , 0.05 , 0.2$ $0.6, 0.15, 0.05, 0.2$ $0.6,0.15,0.05,0.2$ 。

可见转换后所有概率之和为1，且原始数值的大小排序 2.5 > 1.8 > 0.6 > 0.1 2.5>1.8>0.6>0.1 2.5>1.8>0.6>0.1，与概率排序 0.6 > 0.2 > 0.15 > 0.05 0.6>0.2>0.15>0.05 0.6>0.2>0.15>0.05 完全一致，完美实现了"数值→概率"的合理转换。

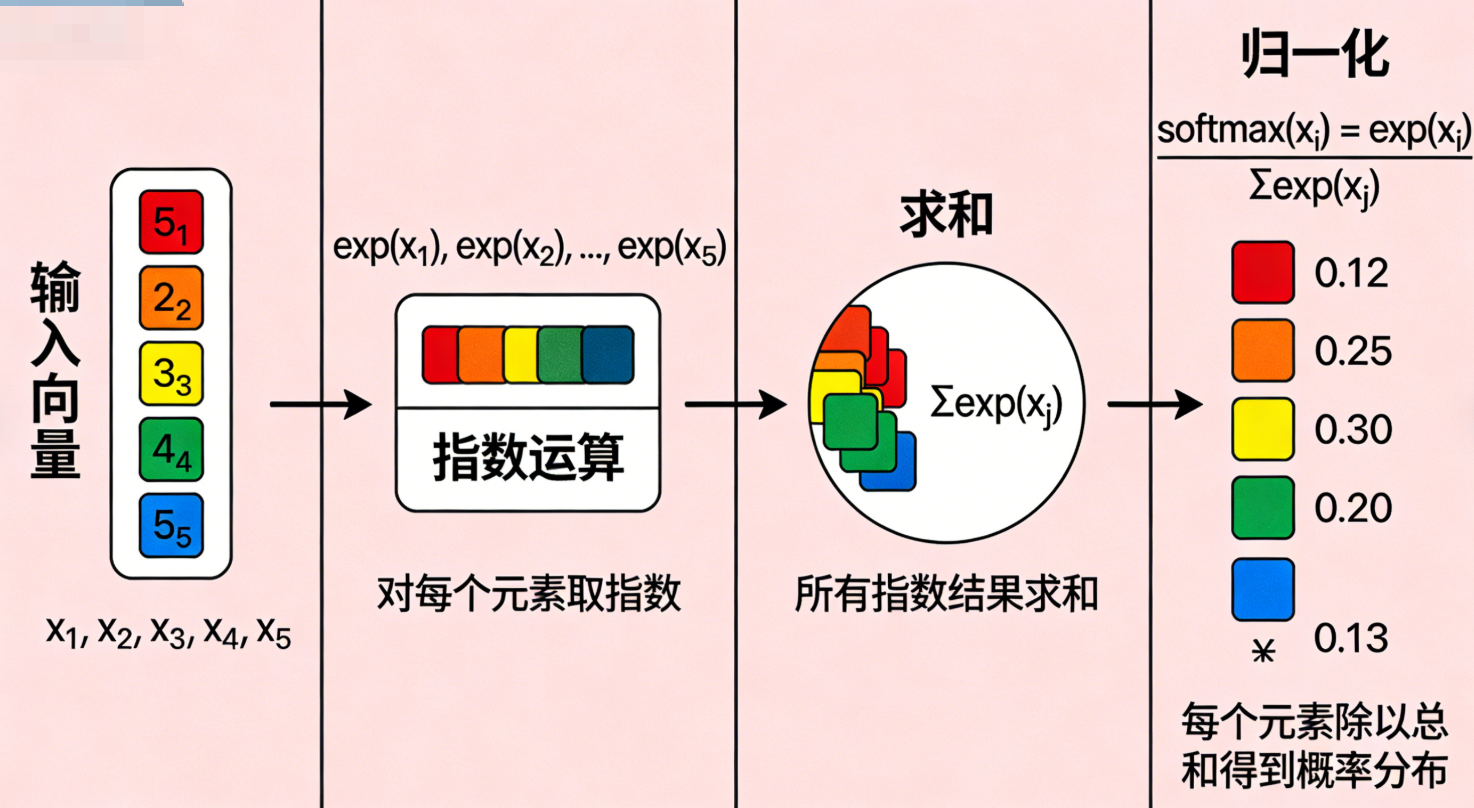
3.8核心适用场景和关键区分： Softmax函数 vs 损失函数

Softmax函数是分类任务的标配组件，常部署在神经网络的最后一层输出端：将模型的原始预测数值转换为各类别的概率后，既可以直观反映模型对不同类别的预测置信度，也能为交叉熵损失函数提供符合要求的概率分布输入，让损失计算更贴合任务本质。

Softmax函数和损失函数（如交叉熵）是分工明确的上下游组件，核心作用、解决问题、数学本质完全不同，二者常配合使用但不可混淆，核心区别如下：

维度	Softmax函数	损失函数（如交叉熵、L1/L2）
核心作用	做数值→概率的格式转换，生成符合概率定义的分布	做误差的量化评估，衡量预测结果与真实值的偏差
解决问题	解决神经网络原始输出无范围、非归一化，无法表示概率的问题	解决正负误差抵消、无法量化模型预测错误的问题
数学本质	是归一化变换函数，仅做数值格式转换，无"误差判断"逻辑	是误差计算函数，基于预测与真实值的对比，输出量化损失值
输出结果	总和为1的概率分布（如 $0.6,0.15,0.05,0.2$ ）	单个非负数值（损失值，如0.85、2.3）
核心目标	让模型输出"可解释的概率"，适配概率类任务的表达需求	让模型感知"预测错了多少"，为参数优化提供评判标准
使用阶段	模型预测输出阶段（最后一层）	模型训练评估阶段（预测后计算）

3.9拓展：归一化并非只有Softmax，只是它是概率归一化的最优选择

归一化是机器学习中通用的数值处理手段，核心是将无约束的数值映射到固定范围，Softmax只是归一化的其中一种方式 ，但它是唯一适配分类任务概率输出的归一化方法。常见的归一化方式还有以下两种，与Softmax适用场景、目标完全不同：

3.9.1. 最值归一化（Min-Max Scaling）

公式： x ′ = x − min ⁡ ( x ) max ⁡ ( x ) − min ⁡ ( x ) x' = \frac{x - \min(x)}{\max(x) - \min(x)} x′=max(x)−min(x)x−min(x)
核心：将数值映射到** $0,1$ ** 固定区间，仅做范围约束，不保证总和为1
适用：数据预处理阶段（如特征值标准化），无概率表达需求的场景
缺陷：对异常值敏感，若数据中有极端值，会导致大部分数值被压缩到极小范围

3.9. 2. 标准化（Z-Score Normalization）

公式： x ′ = x − μ σ x' = \frac{x - \mu}{\sigma} x′=σx−μ（ μ \mu μ为均值， σ \sigma σ为标准差）
核心：将数值映射为均值0、方差1的标准正态分布，无固定取值范围
适用：神经网络隐藏层的数值处理，解决梯度消失/爆炸问题
缺陷：无概率含义，无法直接表示各类别发生的可能性

3.10Softmax作为概率归一化的不可替代性

上述两种归一化虽能约束数值范围，但均无法满足分类任务的概率表达核心要求（总和为1+类别互斥），而Softmax恰好完美适配，这也是它成为分类任务最后一层标配的原因：

输出严格满足概率公理：所有维度值∈ $0,1$ ，且总和=1，可直接解释为"各类别发生的概率"；
贴合分类任务互斥特性：一个类别概率升高，其他类别必然降低，符合"样本只能属于一个类别"的实际场景；
与交叉熵损失完美兼容：交叉熵的核心是计算两个概率分布的差异，Softmax的输出恰好是合法的概率分布，可直接作为其输入。

二者的配合逻辑：神经网络原始输出（logits）→ Softmax概率归一化 → 生成合法概率分布 → 交叉熵损失计算 → 输出量化损失值 → 梯度下降优化模型参数

简单来说：Softmax负责把模型输出"转成能看的概率"，损失函数负责基于这个概率"判断模型预测的好坏"，归一化是基础，误差评估是核心。

四、上下文理解：大模型的"记忆能力"

自然语言的含义高度依赖上下文，比如"他喜欢打篮球，每天都玩它"中的"它"，需要结合前文才能知道指的是"篮球"。大模型的"上下文理解能力"，就是模拟人类的"记忆功能"，让模型能关联前后文的语义。

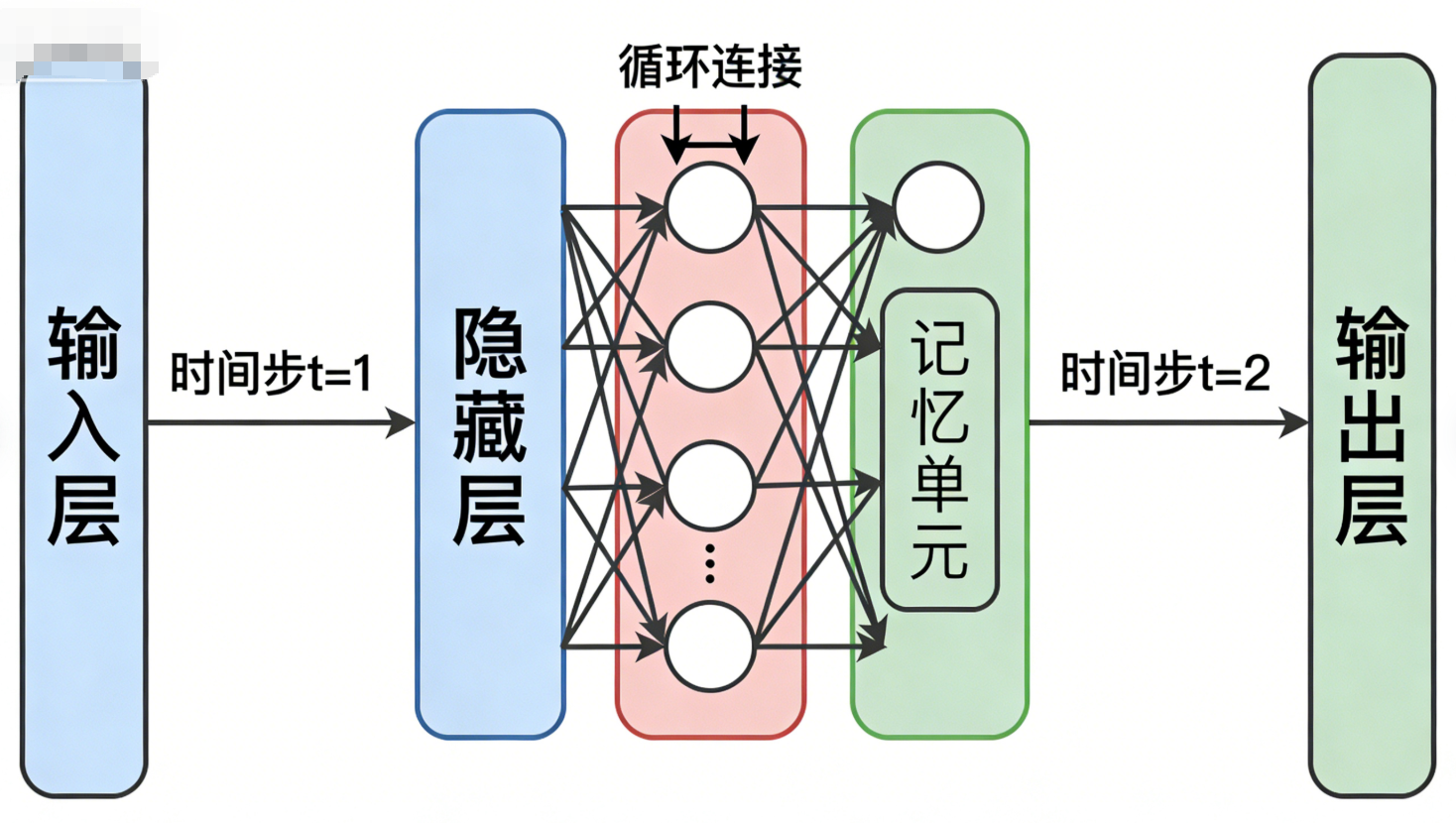
4.1 循环神经网络（RNN）：串行的"记忆模式"

早期的循环神经网络（RNN）通过"输出回环"实现上下文记忆：

模型的输出会作为"隐藏状态"，与下一个Token一起输入模型；
比如处理"我喜欢你的表哥的表哥"时，每个Token会按时间顺序输入，模型会通过隐藏状态记住前文的语义。

但RNN的短板很明显：串行计算导致效率极低------必须等前一个Token处理完成，才能开始处理下一个Token，无法并行计算，难以应对长文本和大规模数据。

你希望在Transformer的自注意力机制部分补充子注意力机制（也常称多头注意力/Multi-Head Attention）的核心内容，我会在原有基础上精简扩充，保持内容简洁且重点突出：

4.2 Transformer：并行的"上下文融合"

2017年Google发表的《Attention Is All You Need》论文，提出了基于"自注意力机制"的Transformer架构，彻底解决了RNN的效率问题。

Transformer的核心是"自注意力机制"：每个Token会主动计算与其他所有Token的"影响力权重"，并根据权重融合上下文信息，无需按时间顺序串行处理。

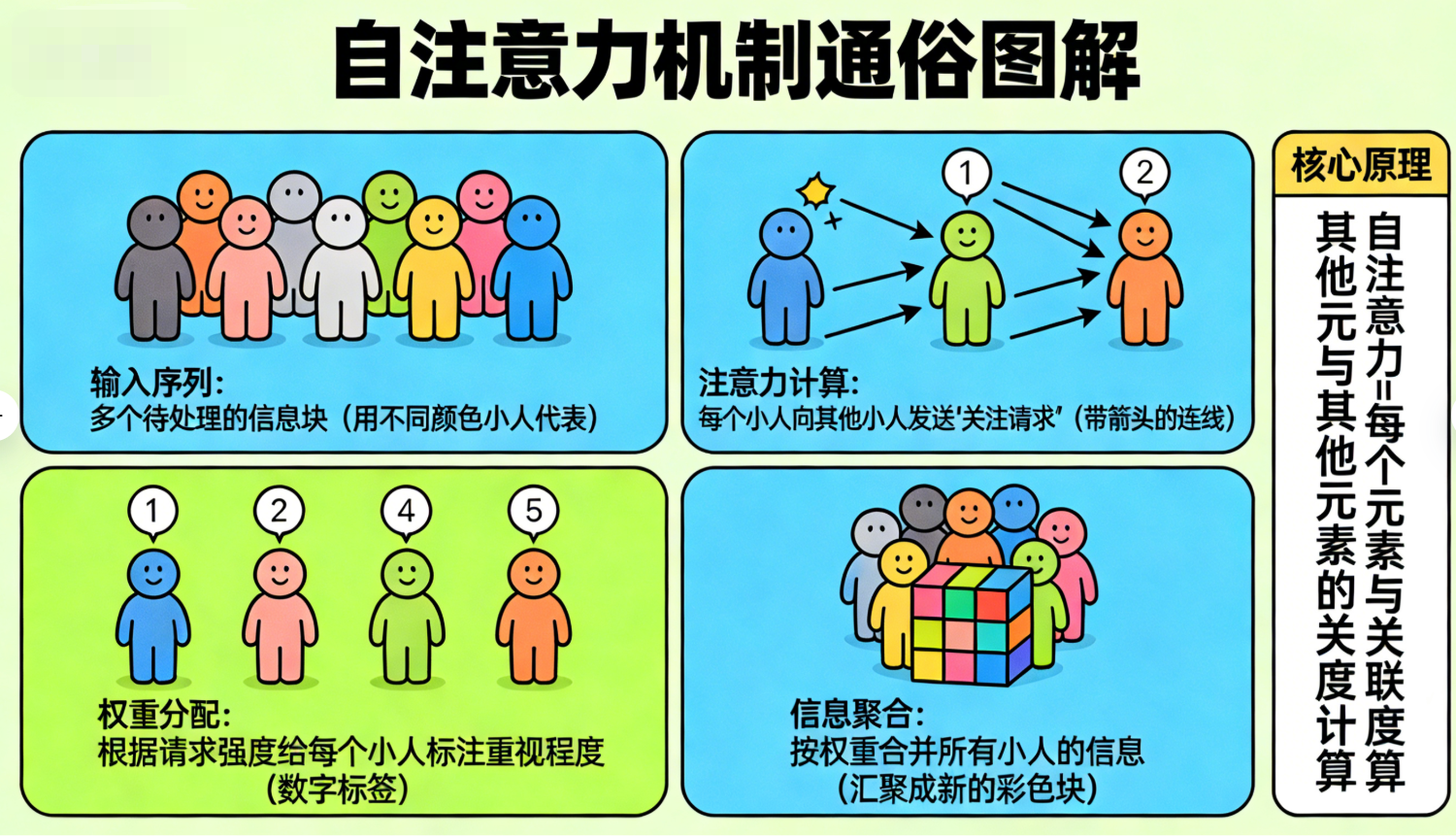
比如处理"新年好"：

"新"会计算与"年""好"的权重，融合二者的语义；
"年"会计算与"新""好"的权重，融合二者的语义；
所有Token的上下文融合可同时进行，实现并行计算。

自注意力机制的数学实现依赖三次矩阵运算（Q、K、V）：

Q（Query）：当前Token的查询向量；
K（Key）：其他Token的关键词向量；
V（Value）：其他Token的价值向量。

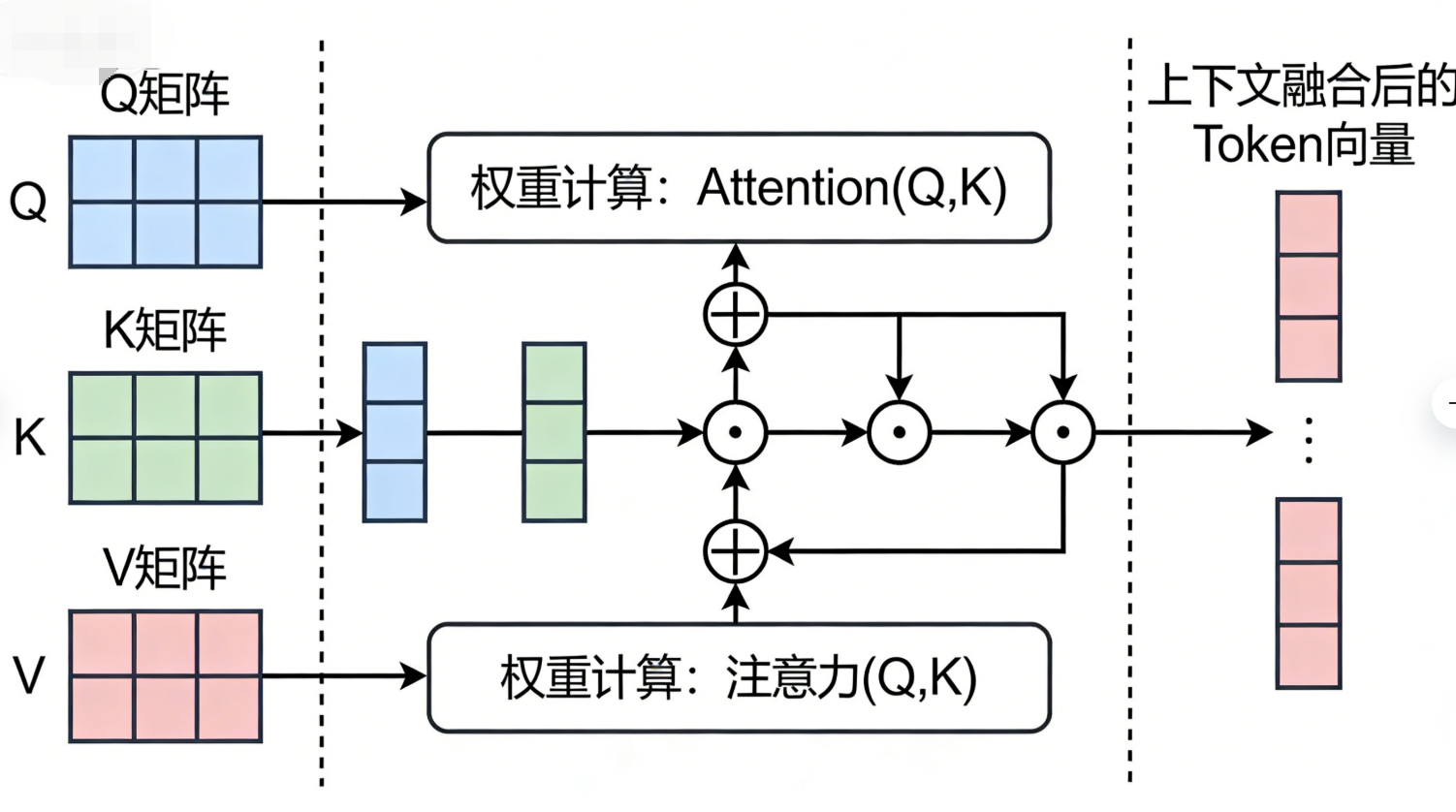
通过Q与K的点积计算权重，再与V加权求和，得到融合上下文后的Token向量。这种方式让模型既能高效融合上下文，又能通过并行计算提升效率。

为了让模型捕捉不同维度的语义信息（比如语法、语义、位置），Transformer进一步提出多头注意力：将Q、K、V拆分为多组独立的子向量，每组子向量单独计算一次自注意力（形成一个"注意力头"），最后将所有头的输出拼接并线性变换，得到最终的上下文向量。简单来说，单头注意力只关注一种上下文关联，多头注意力能同时关注多种关联，让模型的语义理解更全面。

多头注意力是Transformer的核心升级，也是目前绝大多数大模型的基础架构。

自注意力机制通过Q/K/V矩阵运算实现Token间的上下文融合，支持并行计算；
多头（子）注意力将Q/K/V拆分多组独立计算，捕捉多维度语义关联，是Transformer的关键优化。

图示说明：Transformer，左侧为Q、K、V矩阵（英文标注），中间为权重计算过程，右侧为上下文融合后的Token向量。

4.3 稀疏自注意力：效率与效果的"平衡术"

传统自注意力机制需要计算每个Token与其他所有Token的权重，计算量随文本长度呈平方增长。稀疏自注意力机制对此进行了优化：

每个Token仅计算与"重要Token"（如相邻Token、语义相关Token）的权重；
忽略与语义无关的Token，减少计算量，提升推理速度。

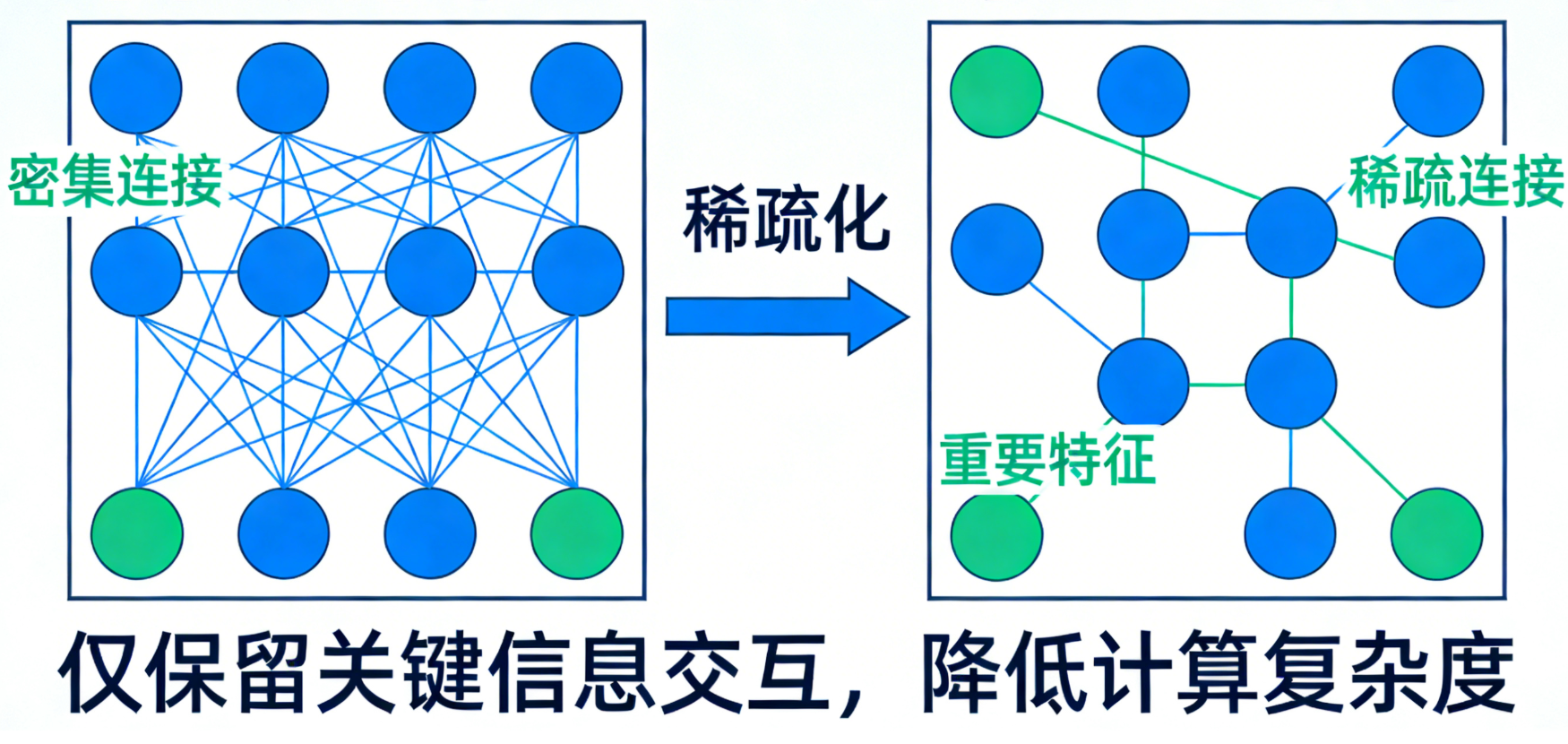
比如处理"我喜欢自然语言处理"，"喜欢"只需计算与"我""自然语言处理"的权重，无需计算与其他无关Token的关系。这种优化让大模型能高效处理更长的文本。

五、大模型的训练：从"随机参数"到"智能模型"

大模型的训练过程，就是通过海量数据调整参数，让模型从"随机初始化"的状态，逐步具备理解和生成语言的能力。这个过程类似人类的"学习成长"------先天的架构（模型结构）很重要，但后天的经历（训练数据）更能塑造能力。

5.1 训练数据：模型的"知识来源"

训练数据是大模型的核心"养分"，其质量和规模直接决定模型的性能上限，没有优质海量的数据，再复杂的模型也无法实现高效语义理解和生成。

规模：主流大模型的训练数据已突破万亿Token，远超早期模型的千万级规模；这些数据涵盖文本、图像、语音等多种形式，其中文本数据占比最高，覆盖书籍、网页、论文、对话等各类场景，为模型提供全方位的知识储备。
质量：经过过滤、筛选的优质数据能让模型学习到准确的知识、规范的表达和正确的逻辑，而低质量数据（如错误信息、低俗内容、逻辑混乱文本）会导致模型出现错误回答、偏见输出，甚至产生有害内容，因此数据清洗是训练前的关键步骤。

训练数据分为两类，二者分工明确、缺一不可：

训练集：用于模型学习和参数调整，是模型获取知识的主要载体，占整体数据的80%-90%左右；
验证集：用于评估模型性能，监控训练过程中的误差变化，避免训练数据"既当运动员又当裁判员"，帮助工程师及时发现训练问题。

模型在验证集上的表现称为"泛化能力"------泛化能力强的模型，能很好地处理未见过的新数据，就像适应能力强的人能快速融入新环境；反之，泛化能力弱的模型，只能应对训练过的内容，无法灵活适配新场景。

5.2 超参数：模型的"调整旋钮"

模型参数（权重、偏置）是训练过程中自动调整的，无需人工干预，而超参数是训练前设定的"外部参数"，相当于模型训练的"调节开关"，直接影响训练效率和最终性能。

模型架构：隐藏层数量、每层节点数量，以及注意力头数量（针对Transformer架构），决定了模型的复杂度和表达能力；架构越复杂，模型潜在的学习能力越强，但对硬件资源的要求也越高。
学习率：参数调整的步长，是最关键的超参数之一；步长过大易跳过最优解，导致模型训练不稳定、误差波动大；步长过小则训练效率极低，需要更多轮次才能达到理想效果，甚至可能陷入局部最优解无法跳出。
批量大小：每次训练输入的语料数量，与学习率相互配合；批量越大，训练效率越高，能更好地利用GPU并行计算能力，但对GPU显存的要求也越高，批量过大会导致显存溢出，批量过小则会使训练误差波动较大。

当模型在验证集上表现不佳时（如误差过高、泛化能力弱），工程师会调整这些超参数，而非修改模型的内部参数，通过反复调试找到最优的超参数组合，让模型达到最佳性能。

5.3 训练过程：批量、步长与轮次

大模型的训练是一个"迭代优化"的过程，核心是通过不断调整参数，降低模型预测误差，本质就是让模型反复"学习"训练数据中的规律，核心概念包括批量、步长与轮次，三者相互关联、协同作用。

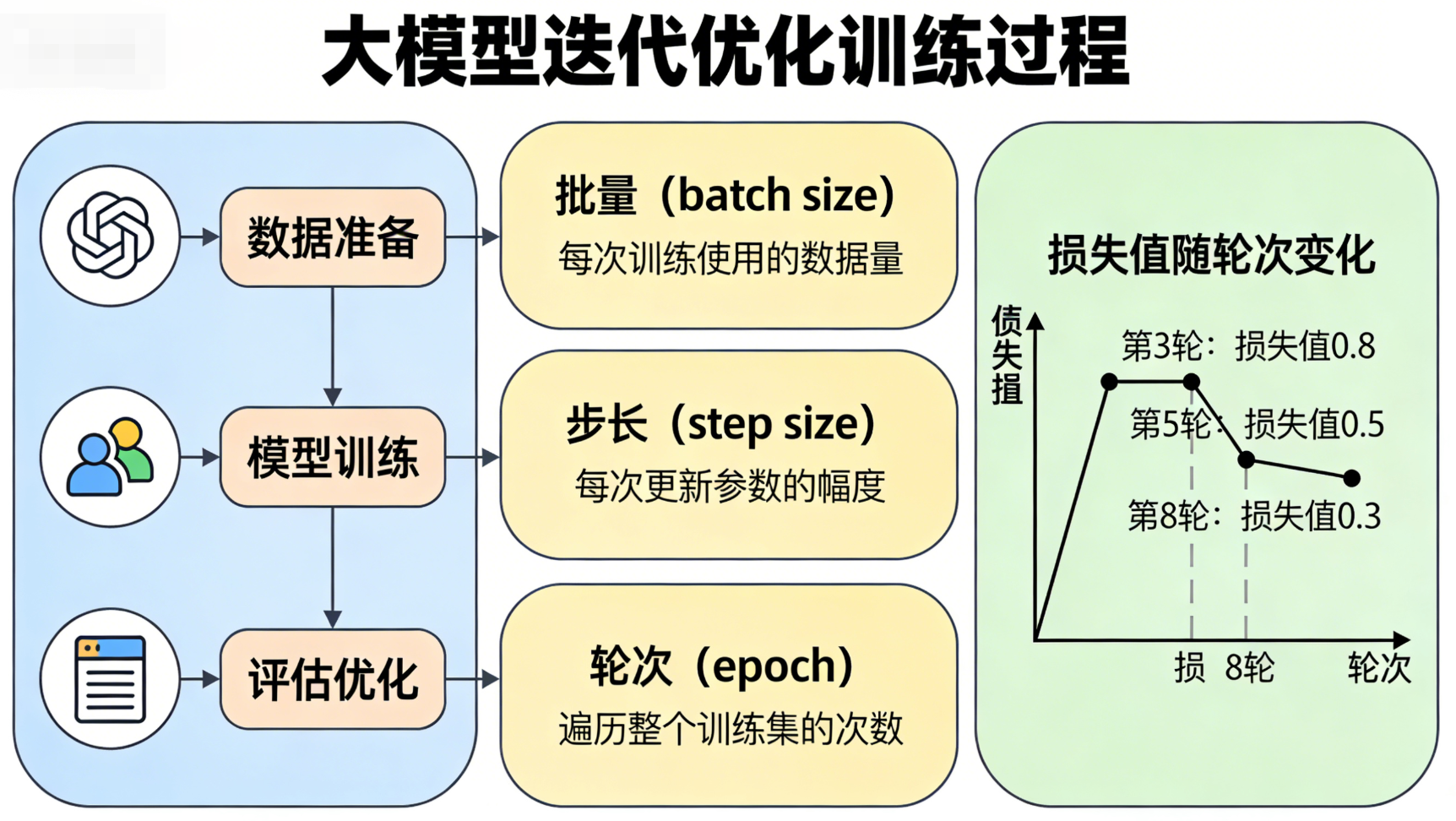
批量（Batch）：一次训练输入的"一批语料"，而非单个Token------批量越大，训练效率越高，能充分利用GPU的并行计算优势，但对GPU显存的要求也越高，超出显存容量会导致训练中断，因此批量大小需结合硬件条件设定。
步长（Step）：每处理一批数据后，模型会根据这批数据的平均预测误差，调整一次自身参数，这个过程称为一个步长（也叫一次迭代）；步长的数量与批量大小、训练集规模相关，训练集越大、批量越小，所需步长越多。
轮次（Epoch）：模型完整遍历一次所有训练数据，称为一个轮次；一轮训练结束后，模型会对所有训练数据的规律有初步掌握，但无法充分学习，因此需要多轮训练。

模型需要多轮训练才能充分学习：每轮训练会打乱数据顺序，避免模型"死记硬背"训练数据（即避免过拟合），让模型真正学习到数据中的通用规律，而非孤立的细节。

5.4 过拟合与欠拟合：训练的"两个陷阱"

训练过程中，工程师的核心目标之一是让模型既"学透"数据，又不"死记"数据，因此需要避免两个常见的训练陷阱------欠拟合与过拟合，二者均会导致模型性能不佳，但成因和表现截然不同。

欠拟合：模型经过多轮训练后，训练误差和验证误差仍很大，无法准确捕捉数据中的规律；原因通常是参数量不足、模型架构过于简单，或者训练轮次不够，导致模型无法拟合复杂的语义关系、逻辑关联，就像学生听课不认真，没学会知识点。
过拟合：模型在训练集上误差很小，几乎能完美预测训练数据，但在验证集上误差很大，泛化能力不足；原因是模型"死记硬背"了训练数据，包括无关细节、偶然规律，甚至数据中的错误，无法适应未见过的新数据，就像学生死记硬背答案，换一道同类题就不会做。

对应的解决方法有明确针对性：增加参数量、优化模型架构（应对欠拟合）；增加训练数据多样性、减少训练轮次、使用正则化方法（应对过拟合），同时调整超参数也能有效缓解这两种问题。

5.5 监督学习与自监督学习：训练的"两种模式"

大模型的训练模式主要分为两种，核心区别在于是否需要人工标注目标值，两种模式各有优劣，目前自监督学习已成为大模型训练的主流方式，解决了海量数据的训练难题。

监督学习 ：目标值需要人工标注，比如给图片打标签（猫/狗）、给文本配对应答、给句子标注情感（正面/负面）；这种方式训练出的模型精度高、针对性强，但标注成本极高，需要大量人力物力，无法应对大模型所需的万亿级海量数据，仅适用于小范围、高精度需求场景。
自监督学习 ：无需人工标注，模型自动从数据中生成目标值，实现"自我学习"；最常见的方式是"掩码预测"，即随机掩盖句子中的部分Token（如用 $MASK$ 替换），让模型根据上下文预测被掩盖的Token。除此之外，还有句子排序、同义句生成等自监督训练方式。

自监督学习彻底解决了海量数据的标注难题，让模型能够高效利用互联网上的海量无标注数据，快速积累知识、提升性能，是目前GPT、BERT等主流大模型的核心训练模式。

5.6 温度系数与知识蒸馏：模型的"优化工具"

大模型训练完成后，还需要通过一些优化工具，调整其输出效果、实现轻量化部署，满足不同场景的需求------训练好的基础大模型往往参数庞大、输出风格固定，无法直接适配所有实际应用，温度系数 和知识蒸馏 是最常用的两种优化工具，二者用途不同、互补性强，分别解决"输出适配"和"部署落地"两大核心问题。

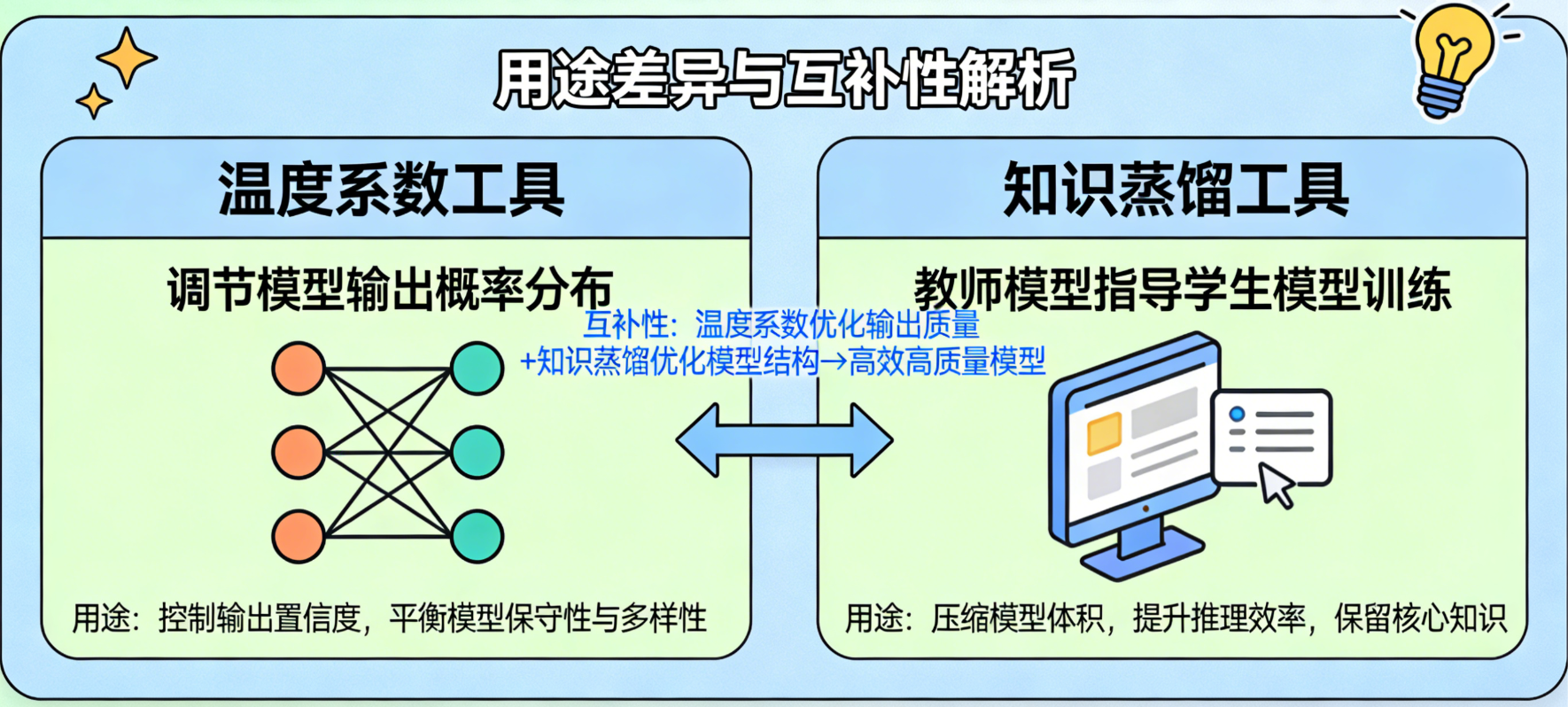
温度系数 （Temperature）：用于调节模型输出的随机性，本质是调整模型输出概率的分布，核心原理是对Softmax输出层的原始得分（logits）进行缩放，再计算概率（温度越低，概率分布越集中；温度越高，概率分布越平缓）。

温度值通常在0-2之间，温度低（如0.0-0.5）时，模型输出更确定，高概率Token的占比会进一步提升，输出更精准、稳定，避免无关信息干扰，适合代码生成、数学解题、专业问答等对准确性要求高的场景；温度高（如1.0-1.5）时，模型输出更多样，低概率Token也可能被选中，打破固定表达模式，输出更有创意，适合创意写作、诗歌创作、文案生成等需要多样性的场景；温度过高（超过2.0）则会导致输出杂乱无章，失去实际意义。
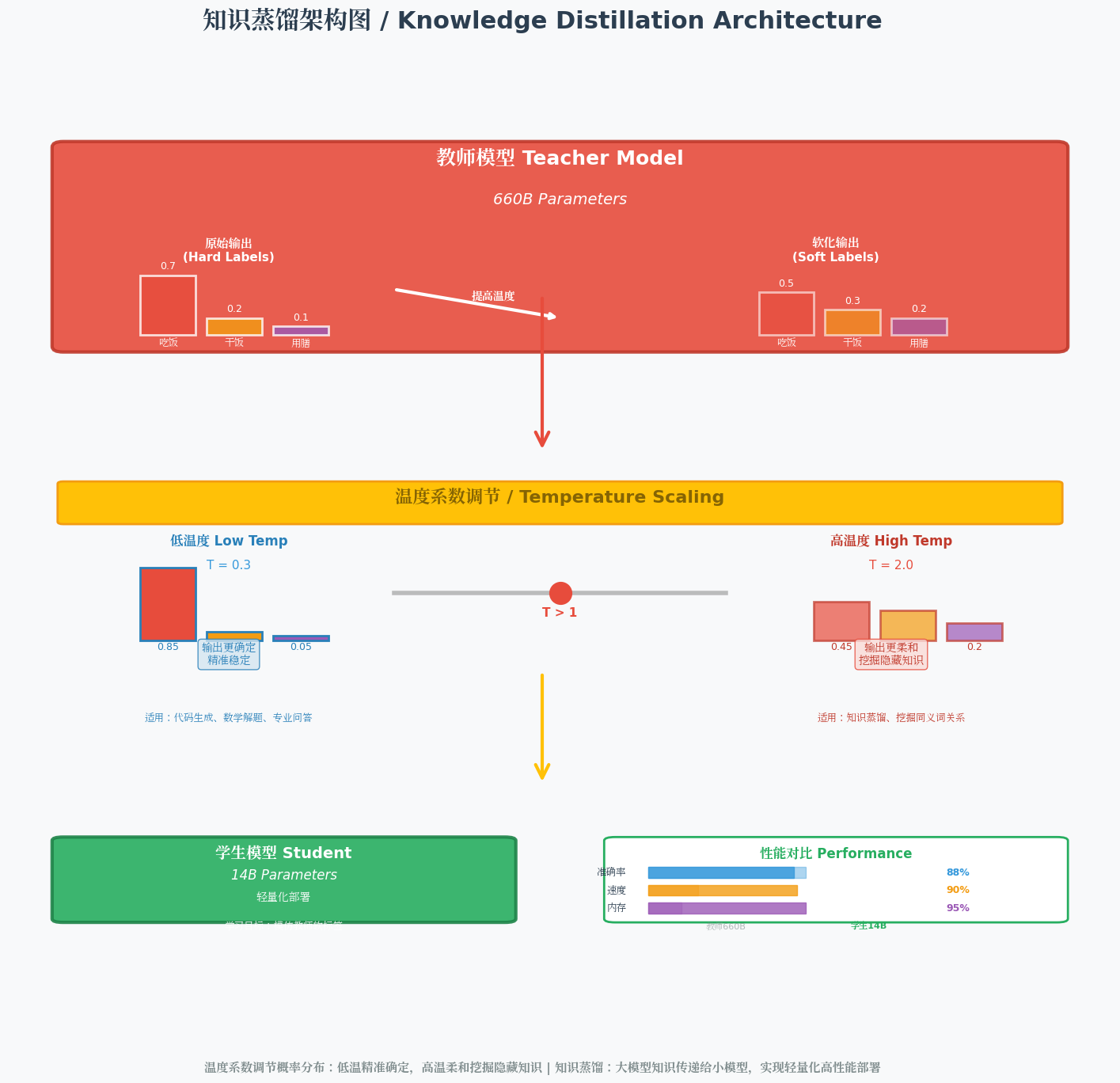
知识蒸馏 （Knowledge Distillation）：核心是"轻量化"，解决大模型参数庞大、显存占用高、部署成本高的痛点，本质是让小模型（学生模型）高效学习大模型（教师模型）的知识和预测逻辑，实现"降参不减能"。

其关键步骤的核心的是借助温度系数：通过提高温度系数（通常设为10-20），让教师模型输出更细腻、更丰富的概率分布，从而挖掘其"隐藏知识"（如"吃饭"的同义词"干饭""用膳"、句子的深层逻辑关联、模糊场景下的决策倾向），而非仅学习教师模型的最终预测结果；再让学生模型以教师模型的输出为"软标签"，结合少量真实数据的"硬标签"进行训练，最终实现"小模型具备接近大模型的性能"。轻量化后的小模型可灵活部署到手机、PC、嵌入式设备等显存有限的场景，大幅降低部署和运行成本，同时保证核心性能不受明显影响。

图示说明：上方为教师模型（英文标注"660B Parameters"），中间为温度系数调节过程（中英双语标注），下方为学生模型（中文标注"14B Parameters"）及性能对比。

六、AI浪潮下的基础设施：算力与网络的支撑

大模型的训练和推理需要海量算力和高效网络的支撑，GPU、并行计算、高速网络成为AI基础设施的核心要素。

6.1 GPU与CUDA：算力的"核心引擎"

大模型的矩阵运算和并行计算高度依赖GPU（图形处理器），与CPU相比，GPU拥有更多计算核心（如英伟达H100 GPU有18000多个CUDA核），能高效处理简单的加减乘除运算------这正是大模型训练和推理的核心需求。

英伟达的CUDA平台提供了GPU并行计算的调度能力，能将复杂的矩阵运算均匀分配给每个CUDA核，实现高效并行计算。没有GPU的强大算力，千亿级参数模型的训练几乎不可能完成。

6.2 并行计算：算力的"规模化提升"

大模型的并行计算分为两类：

数据并行：将训练数据分散到多个GPU，每个GPU运行相同的模型，通过参数服务器聚合梯度，统一更新参数；
模型并行：将模型的参数（张量）分散到多个GPU，每个GPU处理部分神经网络结构，通过AllGather操作拼接计算结果。

现代AI训练多采用"AllReduce"通信方式，摒弃了中心化的参数服务器，让所有GPU直接交换梯度数据，提升通信效率。

七、大模型的使用：从Agent到实用工具

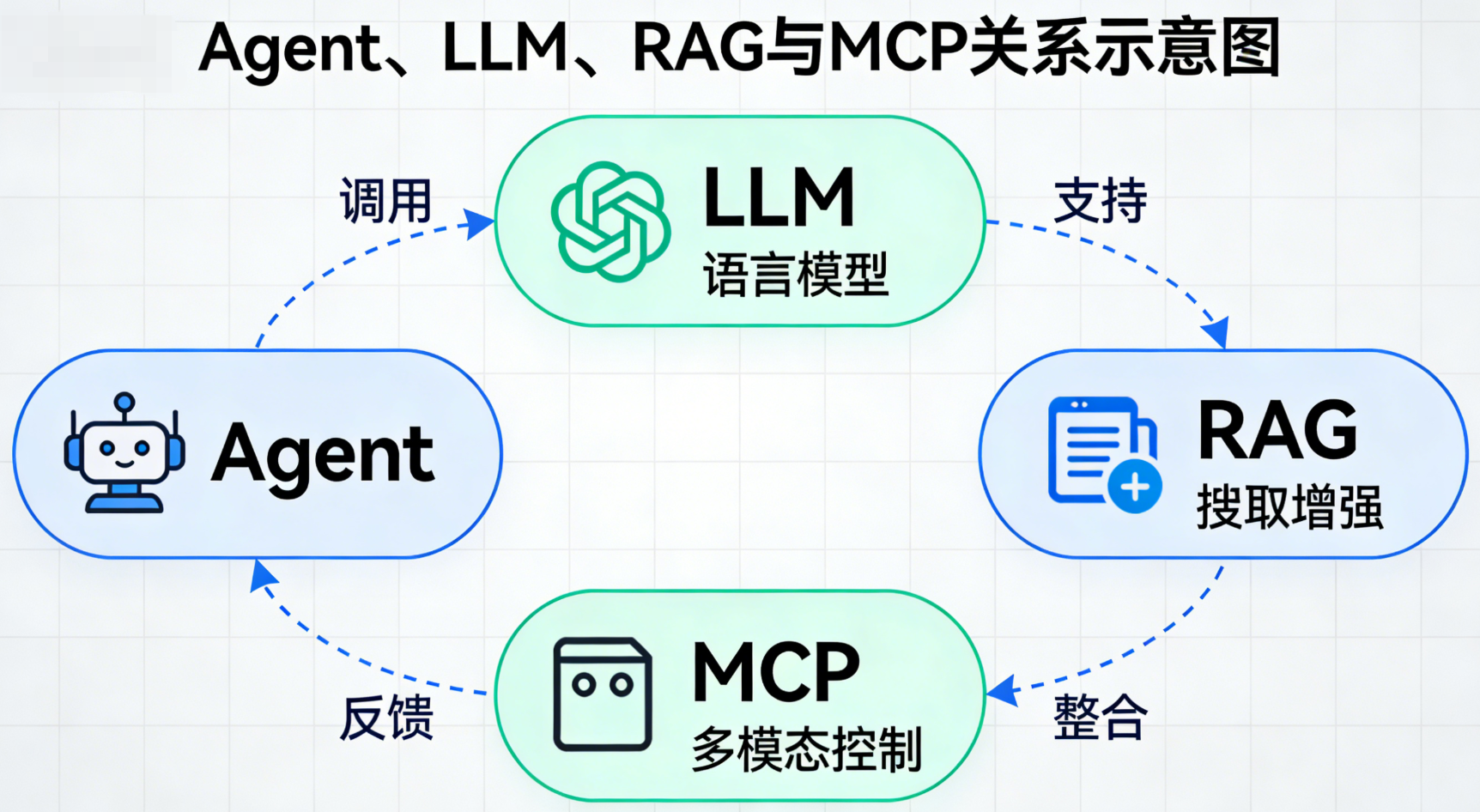
大多数人不会直接接触大模型的底层技术（如训练、参数调优），而是通过Agent、RAG、MCP等上层工具间接使用。这些工具精准解决了大模型的固有缺陷------知识过时、输出幻觉，同时降低了使用门槛，让大模型从"技术黑盒"转变为可落地、可信赖的实用工具，广泛适配日常办公、行业应用等各类场景。

7.1 大模型的不足：知识过时与幻觉

即便经过海量数据训练和优化，基础大模型仍存在两个核心短板，这也是各类上层工具诞生的核心原因，直接影响其实际使用的可靠性：

知识过时：模型训练完成后，内部参数会固定下来，无法主动实时更新知识；其知识范围仅限于训练数据的时间节点，无法获取训练后出现的动态数据（如实时天气、最新新闻、猪肉价格、行业新规等），相当于"停留在过去的知识库"。
幻觉：大模型本质是概率预测模型，核心是基于训练数据中的规律生成最可能的输出，而非基于"事实"；当处理未见过的知识、模糊的提问，或复杂的专业问题时，可能输出不准确、答非所问，甚至编造虚假信息的内容，且输出时会表现得十分确定，难以直接辨别真伪。

7.2 Agent：大模型的"交互入口"

**Agent（智能体）**是普通人使用大模型的核心载体，也是连接用户与大模型底层技术的"桥梁"，它具备完整的"感知-决策-执行"闭环能力，如同大模型的"专属经纪人"，替用户协调所有复杂操作：

感知器：负责接收用户的各类输入（文字、图片、语音、手势等），如同人类的眼、耳、口等感官，能精准捕捉用户的真实需求，无需用户用技术化语言描述。
决策器：由大模型本身担任核心，负责分析用户意图、拆解复杂任务，制定具体的行动方案；比如用户提问"今天适合去公园吗"，决策器会判断需要先查询实时天气，再结合天气情况给出结论。
执行器：负责调用外部工具（如查询天气的API、检索知识库、发送邮件、生成文档等），执行决策器制定的方案，并将最终结果整理后反馈给用户。

Agent最大的价值的是让大模型的使用更自然、更便捷------用户无需了解任何底层技术细节，只需像和人对话一样提出需求，Agent就会自动协调大模型和各类外部工具，完成复杂任务，真正实现"傻瓜式"使用。

7.3 MCP：动态数据的"通信协议"

**MCP（模型上下文协议）**是Agent与外部系统、工具交互的标准化通信协议，核心作用是解决大模型无法处理动态、实时数据的痛点，搭建起"Agent-外部工具-大模型"之间的高效数据通道，让三者能够无缝协同：

数据获取：当Agent需要实时数据或外部信息时，会通过MCP协议，标准化调用对应的外部工具（如天气查询工具、新闻检索工具、股票行情工具等），快速获取所需的动态数据。
数据格式化：外部工具返回的原始数据（如杂乱的接口数据、未整理的文本），会经过MCP协议格式化处理，转换为大模型能够识别、理解的上下文格式，再传递给大模型作为生成答案的依据。

7.4 RAG：消除幻觉的"外部知识库"

RAG（检索增强生成）是解决大模型幻觉和知识过时两大核心短板的关键技术，相当于给大模型额外增加了一块"可实时更新、可追溯的外部存储卡"，让模型能够基于可靠数据生成答案，而非单纯依赖内部固定知识：

知识库构建：将最新的公开数据、企业私域数据（如内部文档、行业资料）、专业知识等，拆分为合适大小的文本片段（Chunk），通过向量转换后存储到向量数据库中，形成可检索、可更新的外部知识库。
检索过程：当用户提出问题时，RAG系统会先对问题进行语义分析，然后在外部知识库中快速检索，找到与问题语义最匹配、最相关的文本片段，筛选出可靠的参考资料。
生成答案：RAG会将检索到的可靠文本片段，与用户的原始问题整合在一起，共同输入大模型；大模型基于这些明确、可追溯的参考数据生成答案，避免了凭空编造信息的情况。

RAG的核心优势在于"无需重新训练模型"，只需更新外部知识库，就能让大模型快速获取最新知识、专业知识，同时让答案具备可追溯性（可查看答案的参考来源），大幅降低幻觉概率，提升输出的准确性和可靠性。

7.5 A2A：Agent之间的"通信标准"

随着Agent的普及和应用场景的复杂化，单一Agent已无法满足用户的综合需求，不同行业、不同功能的Agent之间的通信、协同需求日益增长；A2A协议（Agent-to-Agent）正是为解决这一问题而生，搭建起Agent之间的标准化沟通桥梁。

2025年4月，Google正式发布A2A协议，并将其捐赠给Linux基金会，使其成为Agent之间的中立、开源通信标准，打破了不同厂商Agent之间的"通信壁垒"。

A2A协议让不同功能、不同行业的Agent能够高效协同工作，构建起庞大的Agent生态：比如购物Agent可以调用支付Agent完成交易结算，出行Agent可以调用天气Agent获取实时天气、调用票务Agent预订交通票务，办公Agent可以调用文档Agent生成报告、调用邮件Agent发送通知，让各类Agent各司其职、协同完成复杂的综合任务，进一步拓展大模型的应用边界。

图示说明：以用户查询"今日天气适合出游吗"为例，展示Agent调用MCP获取天气数据、调用RAG获取出游建议的完整流程（中英双语标注）。

7.6 专业技能层：Skill------AI Agent的"智能手册"（LLM的"专业导师"）

Skill 是Anthropic针对大语言模型（LLM）落地行业场景的核心痛点推出的结构化、可复用技能包 ，其核心设计目标是为通用LLM注入领域专属的知识体系、标准化执行流程与合规规则，从根本上解决LLM"懂通用知识但不懂行业规矩、上下文窗口有限导致专业信息承载不足、任务执行无标准化依据"的三大核心问题。

Skill最具创新性的"渐进式信息公开"机制，精准适配LLM的上下文窗口容量限制，既保证专业信息的完整性，又最大化降低Token消耗，实现"按需加载、精准供给"：

会话启动阶段：轻量化元数据加载
AI Agent会预先加载所有已配置Skill的元数据（核心包含技能名称、适用场景、核心能力描述，单条元数据仅占用约100 Token）。此时LLM仅需扫描元数据建立"技能索引"，无需加载任何专业细节，几乎不占用有效上下文空间，确保会话启动阶段的轻量化与高效性。
需求匹配阶段：核心指令精准加载
当LLM通过语义理解匹配到用户需求与某一/某类Skill元数据高度契合时，AI Agent会定向加载该Skill的核心指令集（包含任务执行步骤、核心规则、判断标准等，容量控制在5k Token以内）。这一步为LLM提供完成任务的"核心操作手册"，既满足任务执行的基础需求，又避免无关信息占用上下文。
任务执行阶段：参考资料按需调用
LLM依据核心指令执行具体任务过程中，若需要调取更详细的参考资料（如行业规范、案例库、参数表、合规文档等），AI Agent才会按需加载该Skill关联的支持文件（如reference.md、行业标准PDF、规则清单等），做到"用多少、加载多少"，彻底杜绝Token浪费，同时保证专业信息的可追溯性。

具象化示例：当用户提出需求"帮我审查这段Python代码的安全问题，重点排查注入漏洞和权限管控风险"时，Skill的渐进式加载流程如下：

会话启动时：AI Agent加载"Python代码安全审查Skill"的元数据------"适用场景：Python代码安全合规检测；核心能力：排查注入漏洞、权限管控、数据泄露等12类常见安全风险；执行输出：问题清单+修复建议+合规依据"（仅98 Token），LLM快速建立该技能的索引；
需求匹配时：LLM通过语义匹配识别出用户核心需求是"Python代码安全审查"，且聚焦"注入漏洞、权限管控"，AI Agent随即加载该Skill的核心指令集------包含"安全检查六步法（环境检测→语法扫描→漏洞匹配→风险定级→修复指引→合规校验）""注入漏洞判定规则""权限管控检查维度"等核心内容（约3.2k Token）；
任务执行时：LLM按核心指令逐条审查代码，当需要核对"Python官方安全规范中关于数据库操作权限的具体要求"时，AI Agent才加载该Skill关联的Python_Security_Specification_2025.md参考文件，为LLM提供精准的合规依据，完成风险点的精准判定与修复建议的输出。

八、未来的AI

up to you！🤭