《PyTorch神经网络从开发到调试：实战技巧、可视化与兼容性问题解决方案》

本篇技术博文摘要 🌟

文章首先引导读者实现一个简单的前馈神经网络，详细拆解了网络参数定义、数据生成、模型构建、损失函数与优化器配置以及训练循环等核心步骤，并附有对应的输出结果。

接着，通过可视化梯度下降算法的训练过程，直观展示了模型参数更新的动态效果。

文章的核心部分聚焦于一个完整的二分类任务实战，从非线性数据的生成与说明开始，逐步演示了定义神经网络结构、选择损失函数与优化器、执行模型训练、评估测试性能以及可视化决策边界与损失曲线的全过程，并提供了完整可运行的代码汇总。

最后，文章贴心地汇总了开发中常见的报错（如 matplotlib 版本兼容性问题）及其解决方案，提供了增强的决策边界函数与可视化技巧，旨在帮助读者从理论到实践，全面掌握 PyTorch 神经网络开发，并具备独立排查问题的能力。

引言 📘

在这个变幻莫测、快速发展的技术时代，与时俱进是每个IT工程师的必修课。

我是盛透侧视攻城狮，一名什么都会一丢丢的网络安全工程师，也是众多技术社区的活跃成员以及多家大厂官方认可人员，希望能够与各位在此共同成长。

上节回顾

目录

[本篇技术博文摘要 🌟](#本篇技术博文摘要 🌟)

[引言 📘](#引言 📘)

上节回顾

[1.PyTorch 第一个神经网络](#1.PyTorch 第一个神经网络)

1.1实现一个简单的前馈神经网络示例

1.1.1输出结果

1.1.2定义网络参数：

1.1.3生成输入数据和目标数据：

1.1.4定义神经网络模型：

1.1.5定义损失函数和优化器：

1.1.6训练循环：

2.可视化执行梯度下降算法进行模型训练示例一

2.1结果图

3.神经网络完成简单的二分类任务------示例2

3.1数据准备

3.1.1数据说明：

3.2定义神经网络

3.2.1定义神经网络示例

3.3定义损失函数和优化器

3.4训练模型

3.5测试模型并可视化结果

3.6完整代码汇总

3.7可视化分类边界图及损失输出

4.常见代码报错汇总如下：

[4.1matplotlib 版本存在兼容性问题](#4.1matplotlib 版本存在兼容性问题)

4.2解决方案

[4.2.1.解决 PyCharm 兼容性问题](#4.2.1.解决 PyCharm 兼容性问题)

4.2.2.保存图片而不是直接显示

[4.2.3. 增强的决策边界函数](#4.2.3. 增强的决策边界函数)

[4.2.4. 额外的可视化增强](#4.2.4. 额外的可视化增强)

4.3解决方案代码汇总

欢迎各位彦祖与热巴畅游本人专栏与技术博客

你的三连是我最大的动力

点击➡️指向的专栏名即可闪现

1.PyTorch 第一个神经网络

将介绍如何用 PyTorch 实现一个简单的前馈神经网络，完成一个二分类任务。

网络结构包括输入层、隐藏层和输出层，使用了 ReLU 激活函数和 Sigmoid 激活函数。

采用了均方误差损失函数和随机梯度下降优化器。

训练过程是通过前向传播、计算损失、反向传播和参数更新来逐步调整模型参数。

1.1实现一个简单的前馈神经网络示例

python 复制代码

# 导入PyTorch库
import torch
import torch.nn as nn

# 定义输入层大小、隐藏层大小、输出层大小和批量大小
n_in, n_h, n_out, batch_size = 10, 5, 1, 10

# 创建虚拟输入数据和目标数据
x = torch.randn(batch_size, n_in)  # 随机生成输入数据
y = torch.tensor([[1.0], [0.0], [0.0], 
                 [1.0], [1.0], [1.0], [0.0], [0.0], [1.0], [1.0]])  # 目标输出数据

# 创建顺序模型，包含线性层、ReLU激活函数和Sigmoid激活函数
model = nn.Sequential(
   nn.Linear(n_in, n_h),  # 输入层到隐藏层的线性变换
   nn.ReLU(),            # 隐藏层的ReLU激活函数
   nn.Linear(n_h, n_out),  # 隐藏层到输出层的线性变换
   nn.Sigmoid()           # 输出层的Sigmoid激活函数
)

# 定义均方误差损失函数和随机梯度下降优化器
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)  # 学习率为0.01

# 执行梯度下降算法进行模型训练
for epoch in range(50):  # 迭代50次
   y_pred = model(x)  # 前向传播，计算预测值
   loss = criterion(y_pred, y)  # 计算损失
   print('epoch: ', epoch, 'loss: ', loss.item())  # 打印损失值

   optimizer.zero_grad()  # 清零梯度
   loss.backward()  # 反向传播，计算梯度
   optimizer.step()  # 更新模型参数

1.1.1输出结果

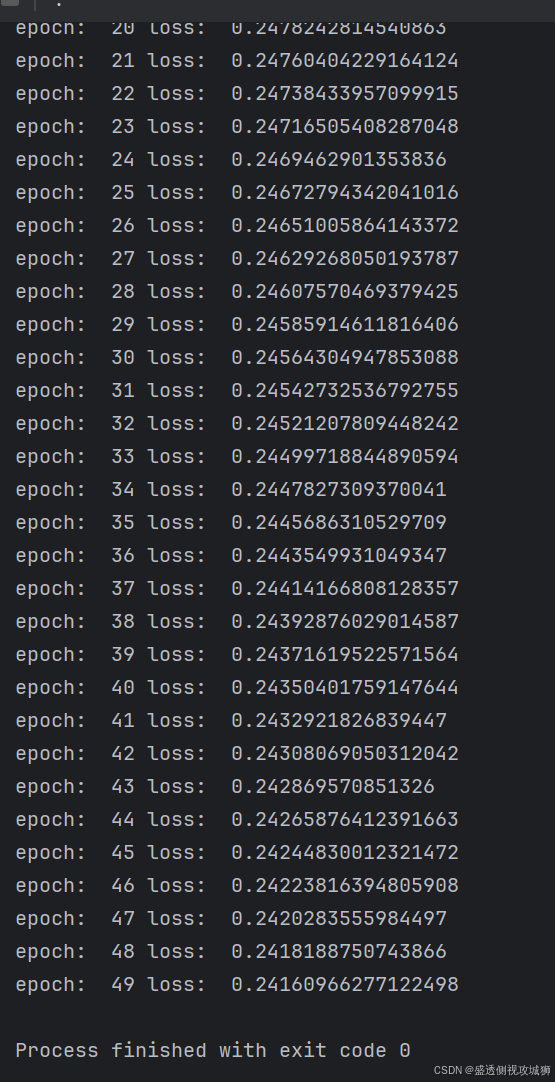
1.1.2定义网络参数：

python 复制代码

n_in, n_h, n_out, batch_size = 10, 5, 1, 10

n_in：输入层大小为 10，即每个数据点有 10 个特征。

n_h：隐藏层大小为 5，即隐藏层包含 5 个神经元。

n_out：输出层大小为 1，即输出一个标量，表示二分类结果（0 或 1）。

batch_size：每个批次包含 10 个样本。

1.1.3生成输入数据和目标数据：

python 复制代码

x = torch.randn(batch_size, n_in)  # 随机生成输入数据
y = torch.tensor([[1.0], [0.0], [0.0], 
                 [1.0], [1.0], [1.0], [0.0], [0.0], [1.0], [1.0]])  # 目标输出数据

x：随机生成一个形状为 (10, 10) 的输入数据矩阵，表示 10 个样本，每个样本有 10 个特征。

y：目标输出数据（标签），表示每个输入样本的类别标签（0 或 1），是一个 10×1 的张量。

1.1.4定义神经网络模型：

python 复制代码

model = nn.Sequential(
   nn.Linear(n_in, n_h),  # 输入层到隐藏层的线性变换
   nn.ReLU(),            # 隐藏层的ReLU激活函数
   nn.Linear(n_h, n_out),  # 隐藏层到输出层的线性变换
   nn.Sigmoid()           # 输出层的Sigmoid激活函数
)

nn.Sequential 用于按顺序定义网络层。

nn.Linear(n_in, n_h)：定义输入层到隐藏层的线性变换，输入特征是 10 个，隐藏层有 5 个神经元。

nn.ReLU()：在隐藏层后添加 ReLU 激活函数，增加非线性。

nn.Linear(n_h, n_out)：定义隐藏层到输出层的线性变换，输出为 1 个神经元。

nn.Sigmoid()：输出层使用 Sigmoid 激活函数，将结果映射到 0 到 1 之间，用于二分类任务。

1.1.5定义损失函数和优化器：

python 复制代码

criterion = torch.nn.MSELoss()  # 使用均方误差损失函数
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)  # 使用随机梯度下降优化器，学习率为 0.01

1.1.6训练循环：

python 复制代码

for epoch in range(50):  # 训练50轮
   y_pred = model(x)  # 前向传播，计算预测值
   loss = criterion(y_pred, y)  # 计算损失
   print('epoch: ', epoch, 'loss: ', loss.item())  # 打印损失值

   optimizer.zero_grad()  # 清零梯度
   loss.backward()  # 反向传播，计算梯度
   optimizer.step()  # 更新模型参数

for epoch in range(50)：进行 50 次训练迭代。

y_pred = model(x)：进行前向传播，使用当前模型参数计算输入数据 x 的预测值。

loss = criterion(y_pred, y)：计算预测值和目标值 y 之间的损失。

optimizer.zero_grad()：清除上一轮训练时的梯度值。

loss.backward()：反向传播，计算损失函数相对于模型参数的梯度。

optimizer.step()：根据计算出的梯度更新模型参数。

2.可视化执行梯度下降算法进行模型训练示例一

python 复制代码

import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# 定义输入层大小、隐藏层大小、输出层大小和批量大小
n_in, n_h, n_out, batch_size = 10, 5, 1, 10

# 创建虚拟输入数据和目标数据
x = torch.randn(batch_size, n_in)  # 随机生成输入数据
y = torch.tensor([[1.0], [0.0], [0.0], 
                  [1.0], [1.0], [1.0], [0.0], [0.0], [1.0], [1.0]])  # 目标输出数据

# 创建顺序模型，包含线性层、ReLU激活函数和Sigmoid激活函数
model = nn.Sequential(
    nn.Linear(n_in, n_h),  # 输入层到隐藏层的线性变换
    nn.ReLU(),            # 隐藏层的ReLU激活函数
    nn.Linear(n_h, n_out),  # 隐藏层到输出层的线性变换
    nn.Sigmoid()           # 输出层的Sigmoid激活函数
)

# 定义均方误差损失函数和随机梯度下降优化器
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)  # 学习率为0.01

# 用于存储每轮的损失值
losses = []

# 执行梯度下降算法进行模型训练
for epoch in range(50):  # 迭代50次
    y_pred = model(x)  # 前向传播，计算预测值
    loss = criterion(y_pred, y)  # 计算损失
    losses.append(loss.item())  # 记录损失值
    print(f'Epoch [{epoch+1}/50], Loss: {loss.item():.4f}')  # 打印损失值

    optimizer.zero_grad()  # 清零梯度
    loss.backward()  # 反向传播，计算梯度
    optimizer.step()  # 更新模型参数

# 可视化损失变化曲线
plt.figure(figsize=(8, 5))
plt.plot(range(1, 51), losses, label='Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss Over Epochs')
plt.legend()
plt.grid()
plt.show()

# 可视化预测结果与实际目标值对比
y_pred_final = model(x).detach().numpy()  # 最终预测值
y_actual = y.numpy()  # 实际值

plt.figure(figsize=(8, 5))
plt.plot(range(1, batch_size + 1), y_actual, 'o-', label='Actual', color='blue')
plt.plot(range(1, batch_size + 1), y_pred_final, 'x--', label='Predicted', color='red')
plt.xlabel('Sample Index')
plt.ylabel('Value')
plt.title('Actual vs Predicted Values')
plt.legend()
plt.grid()
plt.show()

2.1结果图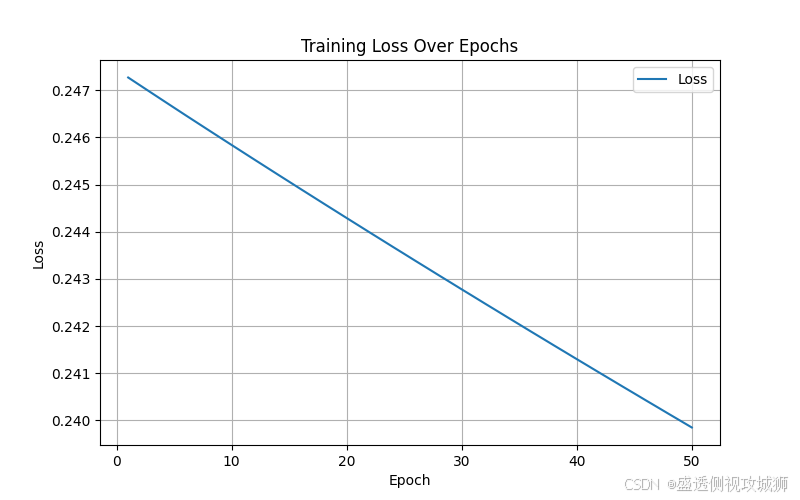

3.神经网络完成简单的二分类任务------示例2

假设有一个二维数据集，目标是根据点的位置将它们分类到两个类别中（例如，红色和蓝色点）。

为更复杂的任务奠定了基础，通过 PyTorch 的模块化接口，神经网络的构建、训练和可视化都非常直观。

3.1数据准备

、首先，我们生成一些简单的二维数据：

python 复制代码

import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt

# 生成一些随机数据
n_samples = 100
data = torch.randn(n_samples, 2)  # 生成 100 个二维数据点
labels = (data[:, 0]**2 + data[:, 1]**2 < 1).float().unsqueeze(1)  # 点在圆内为1，圆外为0

# 可视化数据
plt.scatter(data[:, 0], data[:, 1], c=labels.squeeze(), cmap='coolwarm')
plt.title("Generated Data")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()

3.1.1数据说明：

data 是输入的二维点，每个点有两个特征。

labels 是目标分类，点在圆形区域内为 1，否则为 0。

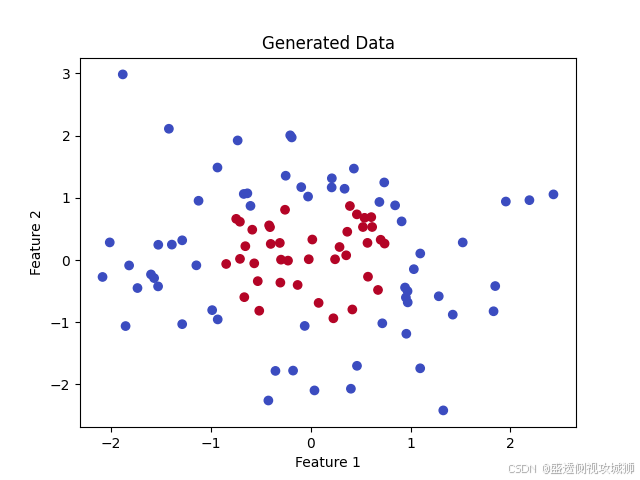
3.2定义神经网络

用 PyTorch 创建一个简单的前馈神经网络。

前馈神经网络使用了一层隐藏层，通过简单的线性变换和激活函数捕获数据的非线性模式。

3.2.1定义神经网络示例

python 复制代码

class SimpleNN(nn.Module):
    def __init__(self):
        super(SimpleNN, self).__init__()
        # 定义神经网络的层
        self.fc1 = nn.Linear(2, 4)  # 输入层有 2 个特征，隐藏层有 4 个神经元
        self.fc2 = nn.Linear(4, 1)  # 隐藏层输出到 1 个神经元（用于二分类）
        self.sigmoid = nn.Sigmoid()  # 二分类激活函数

    def forward(self, x):
        x = torch.relu(self.fc1(x))  # 使用 ReLU 激活函数
        x = self.sigmoid(self.fc2(x))  # 输出层使用 Sigmoid 激活函数
        return x

# 实例化模型
model = SimpleNN()

3.3定义损失函数和优化器

python 复制代码

# 定义二分类的损失函数和优化器
criterion = nn.BCELoss()  # 二元交叉熵损失
optimizer = optim.SGD(model.parameters(), lr=0.1)  # 使用随机梯度下降优化器

3.4训练模型

用数据训练模型，让它学会分类。

python 复制代码

# 训练
epochs = 100
for epoch in range(epochs):
    # 前向传播
    outputs = model(data)
    loss = criterion(outputs, labels)

    # 反向传播
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    # 每 10 轮打印一次损失
    if (epoch + 1) % 10 == 0:
        print(f'Epoch [{epoch + 1}/{epochs}], Loss: {loss.item():.4f}')

3.5测试模型并可视化结果

测试模型，并在图像上绘制决策边界。

python 复制代码

# 可视化决策边界
def plot_decision_boundary(model, data):
    x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
    y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
    xx, yy = torch.meshgrid(torch.arange(x_min, x_max, 0.1), torch.arange(y_min, y_max, 0.1), indexing='ij')
    grid = torch.cat([xx.reshape(-1, 1), yy.reshape(-1, 1)], dim=1)
    predictions = model(grid).detach().numpy().reshape(xx.shape)
    plt.contourf(xx, yy, predictions, levels=[0, 0.5, 1], cmap='coolwarm', alpha=0.7)
    plt.scatter(data[:, 0], data[:, 1], c=labels.squeeze(), cmap='coolwarm', edgecolors='k')
    plt.title("Decision Boundary")
    plt.show()

plot_decision_boundary(model, data)

3.6完整代码汇总

python 复制代码

import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt

# 生成一些随机数据
n_samples = 100
data = torch.randn(n_samples, 2)  # 生成 100 个二维数据点
labels = (data[:, 0]**2 + data[:, 1]**2 < 1).float().unsqueeze(1)  # 点在圆内为1，圆外为0

# 可视化数据
plt.scatter(data[:, 0], data[:, 1], c=labels.squeeze(), cmap='coolwarm')
plt.title("Generated Data")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()

# 定义前馈神经网络
class SimpleNN(nn.Module):
    def __init__(self):
        super(SimpleNN, self).__init__()
        # 定义神经网络的层
        self.fc1 = nn.Linear(2, 4)  # 输入层有 2 个特征，隐藏层有 4 个神经元
        self.fc2 = nn.Linear(4, 1)  # 隐藏层输出到 1 个神经元（用于二分类）
        self.sigmoid = nn.Sigmoid()  # 二分类激活函数

    def forward(self, x):
        x = torch.relu(self.fc1(x))  # 使用 ReLU 激活函数
        x = self.sigmoid(self.fc2(x))  # 输出层使用 Sigmoid 激活函数
        return x

# 实例化模型
model = SimpleNN()

# 定义损失函数和优化器
criterion = nn.BCELoss()  # 二元交叉熵损失
optimizer = optim.SGD(model.parameters(), lr=0.1)  # 使用随机梯度下降优化器

# 训练
epochs = 100
for epoch in range(epochs):
    # 前向传播
    outputs = model(data)
    loss = criterion(outputs, labels)

    # 反向传播
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    # 每 10 轮打印一次损失
    if (epoch + 1) % 10 == 0:
        print(f'Epoch [{epoch + 1}/{epochs}], Loss: {loss.item():.4f}')

# 可视化决策边界
def plot_decision_boundary(model, data):
    x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
    y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
    xx, yy = torch.meshgrid(torch.arange(x_min, x_max, 0.1), torch.arange(y_min, y_max, 0.1), indexing='ij')
    grid = torch.cat([xx.reshape(-1, 1), yy.reshape(-1, 1)], dim=1)
    predictions = model(grid).detach().numpy().reshape(xx.shape)
    plt.contourf(xx, yy, predictions, levels=[0, 0.5, 1], cmap='coolwarm', alpha=0.7)
    plt.scatter(data[:, 0], data[:, 1], c=labels.squeeze(), cmap='coolwarm', edgecolors='k')
    plt.title("Decision Boundary")
    plt.show()

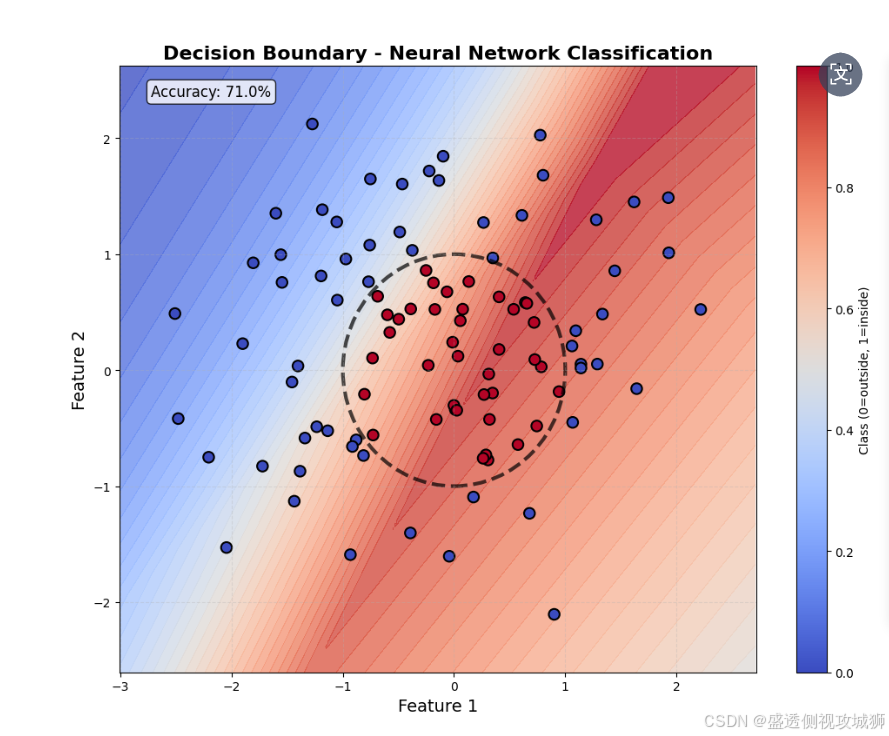
plot_decision_boundary(model, data)

3.7可视化分类边界图及损失输出

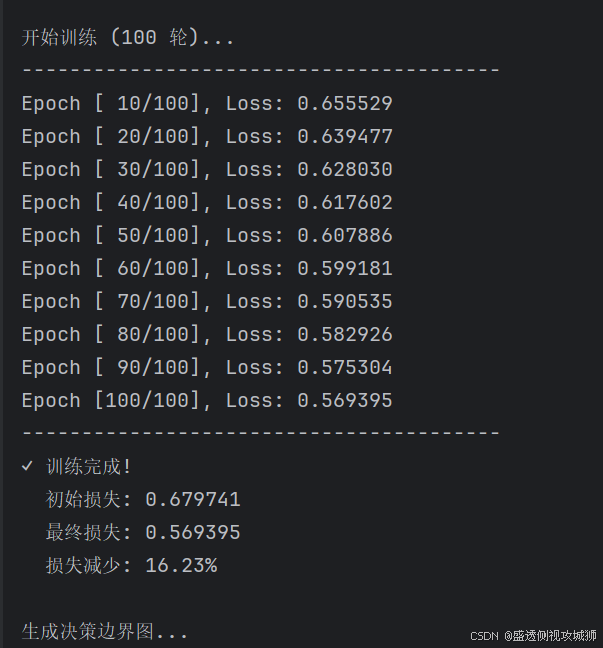
4.常见代码报错汇总如下：

4.1matplotlib 版本存在兼容性问题

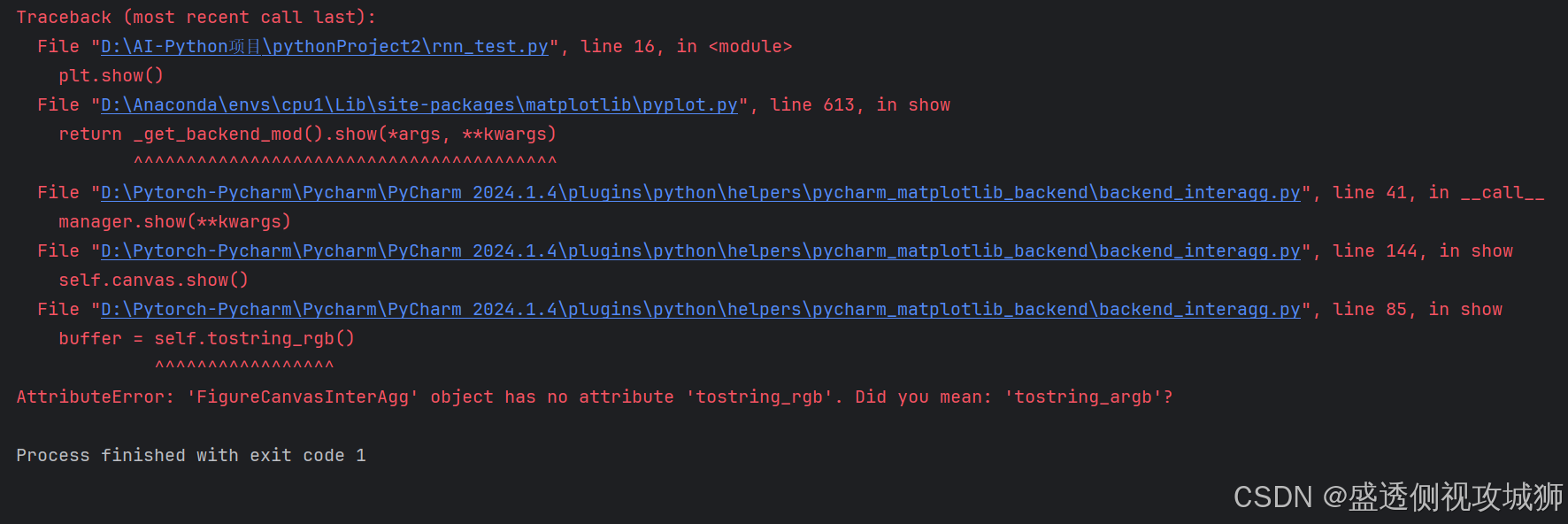
4.2解决方案

4.2.1.解决 PyCharm 兼容性问题

python 复制代码

import matplotlib
matplotlib.use('Agg')  # 使用Agg后端，避免PyCharm内置后端的兼容性问题
import matplotlib.pyplot as plt

4.2.2.保存图片而不是直接显示

python 复制代码

plt.savefig('filename.png', dpi=100, bbox_inches='tight')

4.2. 3. 增强的决策边界函数

使用 np.meshgrid替代 torch.meshgrid避免版本兼容性问题

添加了准确率计算和显示

添加了原始圆边界作为参考

4.2. 4. 额外的可视化增强

生成三个可视化文件：

generated_data.png：原始数据分布

decision_boundary.png：决策边界图

training_loss.png：训练损失曲线

添加了模型评估和样本预测示例

添加了训练过程日志

4.3解决方案代码汇总

python 复制代码

import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib
import numpy as np

# 设置matplotlib后端为Agg，避免PyCharm兼容性问题
matplotlib.use('Agg')
import matplotlib.pyplot as plt

print("=" * 50)
print("神经网络训练与决策边界可视化")
print("=" * 50)

# 生成一些随机数据
n_samples = 100
torch.manual_seed(42)  # 设置随机种子确保可重复性
data = torch.randn(n_samples, 2)  # 生成 100 个二维数据点
labels = (data[:, 0] ** 2 + data[:, 1] ** 2 < 1).float().unsqueeze(1)  # 点在圆内为1，圆外为0

print(f"数据集大小: {n_samples} 个样本")
print(f"数据形状: {data.shape}")
print(f"标签形状: {labels.shape}")
print(f"正样本数量 (圆内): {labels.sum().item()}")
print(f"负样本数量 (圆外): {n_samples - labels.sum().item()}")

# 可视化数据 - 保存图片而不是直接显示
plt.figure(figsize=(8, 6))
plt.scatter(data[:, 0], data[:, 1], c=labels.squeeze(), cmap='coolwarm', s=50, edgecolors='k')
plt.title("Generated Data - Circle Classification")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.colorbar(label="Class (0=outside, 1=inside)")
plt.grid(True, alpha=0.3)

# 添加圆边界用于参考
circle = plt.Circle((0, 0), 1, color='green', fill=False, linestyle='--', linewidth=2)
plt.gca().add_patch(circle)
plt.text(0, 0, 'r=1', ha='center', va='center', fontsize=12, color='green')

plt.tight_layout()
plt.savefig('generated_data.png', dpi=100, bbox_inches='tight')
print(f"✓ 数据可视化已保存为: generated_data.png")


# 定义前馈神经网络
class SimpleNN(nn.Module):
    def __init__(self, input_size=2, hidden_size=4, output_size=1):
        super(SimpleNN, self).__init__()
        # 定义神经网络的层
        self.fc1 = nn.Linear(input_size, hidden_size)  # 输入层有 2 个特征，隐藏层有 4 个神经元
        self.fc2 = nn.Linear(hidden_size, output_size)  # 隐藏层输出到 1 个神经元（用于二分类）
        self.sigmoid = nn.Sigmoid()  # 二分类激活函数

    def forward(self, x):
        x = torch.relu(self.fc1(x))  # 使用 ReLU 激活函数
        x = self.sigmoid(self.fc2(x))  # 输出层使用 Sigmoid 激活函数
        return x


# 实例化模型
model = SimpleNN()
print(f"\n✓ 神经网络模型已创建")
print(f"  输入层: 2 个神经元")
print(f"  隐藏层: 4 个神经元 (ReLU激活)")
print(f"  输出层: 1 个神经元 (Sigmoid激活)")
print(f"  总参数数量: {sum(p.numel() for p in model.parameters())}")

# 定义损失函数和优化器
criterion = nn.BCELoss()  # 二元交叉熵损失
optimizer = optim.SGD(model.parameters(), lr=0.1)  # 使用随机梯度下降优化器

print(f"\n✓ 损失函数: 二元交叉熵损失 (BCELoss)")
print(f"✓ 优化器: 随机梯度下降 (SGD), 学习率: 0.1")

# 训练
epochs = 100
print(f"\n开始训练 ({epochs} 轮)...")
print("-" * 40)

losses = []
for epoch in range(epochs):
    # 前向传播
    outputs = model(data)
    loss = criterion(outputs, labels)

    # 反向传播
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    losses.append(loss.item())

    # 每 10 轮打印一次损失
    if (epoch + 1) % 10 == 0:
        print(f'Epoch [{epoch + 1:3d}/{epochs}], Loss: {loss.item():.6f}')

print("-" * 40)
print(f"✓ 训练完成!")
print(f"  初始损失: {losses[0]:.6f}")
print(f"  最终损失: {losses[-1]:.6f}")
print(f"  损失减少: {(losses[0] - losses[-1]) / losses[0] * 100:.2f}%")


# 可视化决策边界函数
def plot_decision_boundary(model, data, labels):
    print(f"\n生成决策边界图...")

    # 创建网格点
    x_min, x_max = data[:, 0].min() - 0.5, data[:, 0].max() + 0.5
    y_min, y_max = data[:, 1].min() - 0.5, data[:, 1].max() + 0.5

    # 生成网格
    h = 0.02  # 网格步长
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))

    # 将网格点转换为tensor并进行预测
    grid_tensor = torch.tensor(np.c_[xx.ravel(), yy.ravel()], dtype=torch.float32)
    with torch.no_grad():
        Z = model(grid_tensor)
        Z = Z.numpy().reshape(xx.shape)

    # 绘制决策边界
    plt.figure(figsize=(10, 8))

    # 绘制决策边界区域
    plt.contourf(xx, yy, Z, alpha=0.8, cmap='coolwarm', levels=50)

    # 绘制原始数据点
    scatter = plt.scatter(data[:, 0], data[:, 1],
                          c=labels.squeeze(),
                          cmap='coolwarm',
                          edgecolors='k',
                          s=80,
                          linewidth=1.5)

    # 添加原始圆边界作为参考
    circle = plt.Circle((0, 0), 1, color='black', fill=False,
                        linestyle='--', linewidth=3, alpha=0.7)
    plt.gca().add_patch(circle)

    # 设置图表属性
    plt.title("Decision Boundary - Neural Network Classification", fontsize=16, fontweight='bold')
    plt.xlabel("Feature 1", fontsize=14)
    plt.ylabel("Feature 2", fontsize=14)
    plt.colorbar(scatter, label="Class (0=outside, 1=inside)")
    plt.grid(True, alpha=0.3, linestyle='--')

    # 添加准确率信息
    with torch.no_grad():
        predictions = model(data)
        predicted_labels = (predictions > 0.5).float()
        accuracy = (predicted_labels == labels).float().mean().item() * 100

    plt.text(0.05, 0.95, f'Accuracy: {accuracy:.1f}%',
             transform=plt.gca().transAxes,
             fontsize=12,
             bbox=dict(boxstyle='round', facecolor='white', alpha=0.8))

    plt.xlim(x_min, x_max)
    plt.ylim(y_min, y_max)
    plt.tight_layout()

    # 保存图像
    plt.savefig('decision_boundary.png', dpi=100, bbox_inches='tight')
    print(f"✓ 决策边界图已保存为: decision_boundary.png")

    return accuracy


# 生成决策边界图
accuracy = plot_decision_boundary(model, data, labels)

# 可视化训练损失
plt.figure(figsize=(10, 6))
plt.plot(range(1, len(losses) + 1), losses, 'b-', linewidth=2)
plt.xlabel('Epoch', fontsize=12)
plt.ylabel('Loss (BCE)', fontsize=12)
plt.title('Training Loss over Epochs', fontsize=14, fontweight='bold')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('training_loss.png', dpi=100, bbox_inches='tight')
print(f"✓ 训练损失曲线已保存为: training_loss.png")

# 模型评估
print(f"\n" + "=" * 50)
print("模型评估结果")
print("=" * 50)
print(f"测试准确率: {accuracy:.2f}%")

# 打印几个样本的预测结果
print(f"\n样本预测示例:")
with torch.no_grad():
    test_samples = 5
    test_indices = torch.randint(0, n_samples, (test_samples,))

    for i, idx in enumerate(test_indices):
        sample = data[idx].unsqueeze(0)
        true_label = labels[idx].item()
        prediction = model(sample).item()
        predicted_class = 1 if prediction > 0.5 else 0

        print(f"  样本 {i + 1}:")
        print(f"    特征: [{sample[0, 0]:.3f}, {sample[0, 1]:.3f}]")
        print(f"    真实标签: {int(true_label)}")
        print(f"    模型输出: {prediction:.4f}")
        print(f"    预测类别: {predicted_class} {'✓' if predicted_class == true_label else '✗'}")
        print(f"    是否正确: {'是' if predicted_class == true_label else '否'}")

print(f"\n" + "=" * 50)
print("训练完成!")
print("=" * 50)
print(f"生成的文件:")
print(f"  1. generated_data.png - 原始数据分布图")
print(f"  2. decision_boundary.png - 决策边界图")
print(f"  3. training_loss.png - 训练损失曲线")
print(f"\n模型准确率: {accuracy:.2f}%")
print("=" * 50)

# 尝试用系统默认程序打开图片（可选）
try:
    import webbrowser
    import os

    if os.path.exists('decision_boundary.png'):
        webbrowser.open('decision_boundary.png')
        print("✓ 已尝试自动打开决策边界图")
except:
    pass

欢迎各位彦祖与热巴畅游本人专栏与技术博客

你的三连是我最大的动力

点击➡️指向的专栏名即可闪现

➡️计算机组成原理****
➡️操作系统
➡️****渗透终极之红队攻击行动********
➡️ 动画可视化数据结构与算法
➡️ 永恒之心蓝队联纵合横防御
➡️****华为高级网络工程师********
➡️****华为高级防火墙防御集成部署********
➡️ 未授权访问漏洞横向渗透利用
➡️****逆向软件破解工程********
➡️****MYSQL REDIS 进阶实操********
➡️****红帽高级工程师
➡️红帽系统管理员********
➡️****HVV 全国各地面试题汇总********