数字测速方法和PID控制

文章目录

前言
一、数字测速方法
- [1.1 M法测速（测频法）](#1.1 M法测速（测频法）)
- [1.2 T法测速（测周法）](#1.2 T法测速（测周法）)
- [1.3 M/T法（混合法）](#1.3 M/T法（混合法）)
二、PID算法
- [2.1 控制概念](#2.1 控制概念)
- [2.2 什么时候要用到PID](#2.2 什么时候要用到PID)
- [2.3 PID的数学表达式及含义](#2.3 PID的数学表达式及含义)
- [2.4 从数学表达式到代码](#2.4 从数学表达式到代码)
- [2.5 PID在电机控制中的使用](#2.5 PID在电机控制中的使用)
总结

前言

电力拖动自动控制系统中各种系统都是通过控制电动机的转速来实现的，而控制电动机转速就要获取电动机转速即对电动机测速和设计合适的控制算法，下面将对旋转编码器的数字测速方法和PID控制进行介绍。

一、数字测速方法

我们如何通过旋转编码器（Encoder）传回来的脉冲信号，算出发动机转了多快？

下面介绍三种测量方法，M法，T法，M/T法

为了方便理解，我们先设定几个角色：

编码器（Encoder） ：电机转一圈，它发出 Z Z Z个脉冲（比如1024个）。
高频时钟（Clock） ：一个跑得很快的计时器，频率为 f 0 f_0 f0（比如1MHz，即1微秒跳一次）。
采样周期（ T c T_c Tc）：你的单片机每隔多久计算一次速度（比如10ms）。

为了理解后面的公式推导，首先来看怎么用"脉冲频率 f e n c f_{enc} fenc"表示"转速 n n n"？

n ( r / m i n ) = f e n c ( 脉冲 / 秒 ) × 60 ( 秒 / 分 ) Z （脉冲 / 转） n(r/min) = \frac{f_{enc}(脉冲/秒) \times 60(秒/分)}{Z（脉冲/转）} n(r/min)=Z（脉冲/转）fenc(脉冲/秒)×60(秒/分)

化简得：
n = 60 × f e n c Z ，公式 A n=\frac{60 \times f_{enc}}{Z}，公式A n=Z60×fenc，公式A

所有的M法、T法、M/T法，本质上都是在用不同的方式计算 f e n c f_{enc} fenc（每秒有多少个脉冲），然后代入(公式A)。

1.1 M法测速（测频法）

M法测速类似于你要算每秒能跑多少米，你先跑 T c T_c Tc秒，看跑了多少米，然后除一下。

过程：

设定一个固定的采样时间 T c T_c Tc（单位：秒）。
在这段时间内，计数器数到了 M 1 M_1 M1个编码器脉冲。
那么，编码器的平均频率 f e n c f_{enc} fenc是多少？ f e n c = 总脉冲数总时间 = M 1 T c f_{enc}=\frac{总脉冲数}{总时间}=\frac{M_1}{T_c} fenc=总时间总脉冲数=TcM1

代入公式A: n = 60 Z × f e n c = 60 Z × M 1 T c n=\frac{60}{Z} \times f_{enc} = \frac{60}{Z} \times \frac{M_1}{T_c} n=Z60×fenc=Z60×TcM1

最终公式： n = 60 M 1 Z T c n=\frac{60M_1}{ZT_c} n=ZTc60M1

M法测速类比站在路边，规定1分钟（采样时间 T c T_c Tc）内，数有多少辆车（脉冲个数 M 1 M_1 M1）经过。

它的问题 ：
高速时很好 ：车很多，你数了1000辆或1001辆，误差只有0.1%，很准。
低速时很烂：假如车很慢，1分钟内只过去了2辆车。万一第3辆车车头刚露出来时间就到了，你没数进去。你数到的就是2。

因此，M法适合高速测量。

1.2 T法测速（测周法）

T法测速类似于你要算每秒跑多少米，这次你只跑一步（1个脉冲间隔），用秒表记录这一步花了多长时间。

过程：

我们只测相邻两个脉冲之间 的时间间隔 T t T_t Tt
这个时间怎么测？用高频时钟 f 0 f_0 f0来数。
假设两个脉冲之间，高频时钟数了 M 2 M_2 M2个数。
那么，这一个脉冲的时间间隔 T t T_t Tt是多少？ T t = M 2 f 0 （单位：秒） T_t = \frac{M_2}{f_0} （单位：秒） Tt=f0M2（单位：秒）
知道了走一步（1个脉冲）的时间，频率 f e n c f_{enc} fenc（1秒能走几步）就是时间的倒数： f e n c = 1 T t = 1 M 2 / f 0 = f 0 M 2 f_{enc} = \frac{1}{T_t}=\frac{1}{M_2 /f_0} = \frac{f_0}{M_2} fenc=Tt1=M2/f01=M2f0
代入公式A： n = 60 Z × f e n c = 60 Z × f 0 M 2 n=\frac{60}{Z} \times f_{enc} = \frac{60}{Z} \times \frac{f_0}{M_2} n=Z60×fenc=Z60×M2f0

最终公式： n = 60 f 0 Z M 2 n=\frac{60f_0}{ZM_2} n=ZM260f0

T法测速类比：既然车很少，那我只等两辆车（相邻两个脉冲），手里拿个毫秒表（高频时钟），看这两辆车之间隔了多少毫秒（时钟脉冲数 M 2 M_2 M2）。

它的问题（痛点） ：
低速时很好 ：车慢，两辆车间隔时间长，你的毫秒表能数出很大一个数字（比如10000），少计一个数误差很小。
高速时很烂：车太快了，两辆车几乎同时过去。你的毫秒表可能只来得及跳一下或者没跳。

结论：T法适合低速测量。

1.3 M/T法（混合法）

这是最完美的物理定义------速度 = 真实位移 / 真实时间。

回顾M法和T法的缺陷 ：

M法：时间 T c T_c Tc是准的，但脉冲数 M 1 M_1 M1可能少算半个（因为时间到了强行截断），导致位移不准。

T法：脉冲数是准的（就是1个），但如果转速极快，时间 T c T_c Tc太短，误差大。

M/T法的过程：

我们在一段时间内，同时记录两个数据：

真实位移 ：也就是这段时间内，编码器到底发了多少个完整的脉冲？记为 M 1 M_1 M1。
真实时间 ：这 M 1 M_1 M1个脉冲，到底花了多少精确时间？

怎么记录精确时间？

我们用高频时钟数数，记为 M 2 M_2 M2

那么，真实时间 T c = M 2 f 0 T_c = \frac{M_2}{f_0} Tc=f0M2

根据定义计算频率 f e n c f_{enc} fenc： f e n c = 真实脉冲数真实时间 = M 1 M 2 / f 0 = M 1 f 0 M 2 f_{enc}=\frac{真实脉冲数}{真实时间}=\frac{M_1}{M_2/f_0}=\frac{M_1f_0}{M_2} fenc=真实时间真实脉冲数=M2/f0M1=M2M1f0
代入公式A： n = 60 Z × f e n c = 60 Z × M 1 f 0 M 2 n=\frac{60}{Z}\times f_{enc}= \frac{60}{Z}\times \frac{M_1f_0}{M_2} n=Z60×fenc=Z60×M2M1f0

最终公式： n = 60 f 0 M 1 Z M 2 n=\frac{60f_0M_1}{ZM_2} n=ZM260f0M1

以上公式n单位为转/分，若采用弧度转，需乘上 2 π 60 \frac{2\pi}{60} 602π

M/T法测速把前两者的优点结合起来，同时数编码器脉冲和时钟脉冲。

原理步骤：

设定一个大概的检测时间 T c T_c Tc(比如10ms)。
但是，当时间到了 T c T_c Tc时，如果在这个时刻没有收到编码器的脉冲，我不马上停止计数！
我会多等一会儿，直到收到下一个编码器脉冲的上升沿，才同时停止两个计数器。
这保证了：我计录的编码器脉冲 M 1 M_1 M1是完整的整数，我记录的时间 M 2 M_2 M2也是严格对应这些脉冲的总时间的。

类比：

老板让你统计车流量，让你大概统计1分钟。

1分钟到了，正好有一辆车开到一半。如果你这时候掐表，那这半辆车算不算？算时间准不准？

M/T法的做法是：1分钟到了，我看一眼路口，只要没有车刚好压线，我就停；如果有车在中间，我就等这辆车完全过去了再掐表。虽然时间比1分钟多了一点点，但我统计的车数（ M 1 M_1 M1）和总耗时（ M 2 M_2 M2）是严格对应的。

全范围适用：低速时，测量时间会自动延长以保证精度；高速时， M 1 M_1 M1很大，精度也高。

小结：

方法	中文名	测量对象	适用场景	为什么
M法	测频法	固定时间，数脉冲	高速	脉冲多，少算一个脉冲影响不大（分母大，分子误差小）
T法	测周法	固定脉冲，数时钟	低速	间隔长，时钟跳得多，计时准（分子固定，分母大）
M/T法	混合法	动态时间，全都要	全范围	自动对齐脉冲边缘，消除了 ± 1 \pm 1 ±1的半个脉冲误差

现在的MCU（微控制器）内部都有专门的定时器/计数器和输入捕获单元，或者专门的正交编码器接口。

M法 = 定时中断读寄存器。

T法 = 输入捕获两个边沿的时间差。

M/T法 = 结合两者，在定时中断里不急着算，等下一个捕获中断来了再算。

二、PID算法

2.1 控制概念

开环控制：只有输入，没有反馈。做了就不管了。系统的输出量（比如转速）不会返回来影响控制端。控制器只根据给定的输入指令工作，不检查执行结果对不对。

生活中的电风扇就是开环控制，你按下"3档"，风扇就按3档的功率转。如果电压低了，或者扇叶积灰转不动了，风扇自己是不知道的，转慢了也就转慢了，它不会自动加速。

电机控制中的开环：给直流电机加 100V 电压，理论上它应该转 1000转。但如果这时候加上负载（比如带了个重物），转速掉到了 800转。因为没有测速元件，系统不知道速度掉了，电压还是保持 100V，转速就一直只有 800转。

以上可以看出开环控制，结构简单、成本低、稳定性好（不会震荡），但精度差，抗干扰能力差。

闭环控制：有反馈，有比较，有修正 。把输出量（转速）检测出来，反馈回来与输入量（目标转速）进行比较，用它们的差值（误差）去控制系统。

生活中的空调就是闭环控制，你设定 26℃。空调通过温度传感器检测室温。如果室温 30℃，它就拼命制冷；如果室温降到 26℃，它就降低功率或停机。它时刻在"看"结果。

电机控制中的闭环：测速发电机/编码器检测实际转速，实际转速 800转，目标 1000转，产生误差200转，控制器看到误差，自动增加电压，直到实际转速回到 1000转。

以上闭环控制控制精度高，能抑制干扰（负载变化不影响转速），但结构复杂，参数调不好容易震荡

PID控制是闭环控制系统里最经典、最通用的控制器。闭环系统里，把误差 e(t) 拿到了，具体该怎么用这个误差去计算控制电压？这就是 PID 负责的事。

它做了三件事：

P (比例)：误差大，我就用力推。（现在）
I (积分)：误差一直消除不掉，我就积累力量慢慢推，直到误差为0。（过去）
D (微分)：误差变化太快，我就反向用力阻尼一下，防止冲过头。（未来）

PID调参参考这篇文章，仿真调参环境可以进小球调参和无人机模拟调参加深对PID的理解。

2.2 什么时候要用到PID

系统需要高精度，且不能有静差
场景：传送带速度必须稳定在 1m/s，不能因为放了一个箱子上去就变慢。
对策：必须用闭环，且必须用 PID 中的 PI（比例积分），因为 I 能消除静差。
系统会有外部干扰（负载变化）
场景：无人机在飞，风会把它吹歪。电梯上人多人少，电机负载完全不同。
对策：开环搞不定，必须用 PID 闭环来自动抵抗这些干扰。
线性或近似线性的系统
场景：电机调速、温度控制、液位控制、压力控制。
对策：这些是 PID 的"主场"。
你不知道系统的精确数学模型
场景：给你一个黑盒子电机，没铭牌，不知道参数。
对策：用 PID。因为 PID 可以通过"试凑法"（调参数）来适应系统，而不需要像"现代控制理论（极点配置、LQR）"那样先去解微分方程。

2.3 PID的数学表达式及含义

P算法： u = K p ∗ e k u = K_p * e_k u=Kp∗ek------ "现在的力量"

作用：只要有误差，马上响应。 K p K_p Kp越大，响应越快。
P算法的作用是减小测量值和理论值之间的误差（差值），让测量值不断接近理论值。

缺点：永远消灭不了静差。

I算法： u = K i ∑ j = 0 k e j u = K_i \sum^{k}_{j=0}e_j u=Ki∑j=0kej ------ "过去的积累"

作用：消除静差。只要误差存在，积分项就会一直累加，输出越来越大，直到把误差彻底顶回去变成0。
I算法的作用是消除稳态误差。当系统误差已经接近0时，P的输出会很小，起不到继续减小误差的作用，导致误差值时钟没法到0.这时就需要用到I算法，让误差不断累加，并将累加后的值输出。

I算法常用于追求更精确的控制。

缺点：导致相位滞后和超调。

D算法： u = K d × ( e ( k ) − e ( k − 1 ) ) u=K_d \times(e(k)-e(k-1)) u=Kd×(e(k)−e(k−1))------ "未来的预测"

作用：抑制超调。当发现误差正在快速减小时，D项会计算出一个负值，抵消P和I的力量，提前减速。
D算法的作用是"阻尼" 。如果系统误差很大或P参数较大，那么P的输出就会很大，导致系统剧烈响应，出现过冲现象，此时就需要用到D算法来抑制，让系统可以刚好停在理论值而不过冲。

就好像在水里挥拳，挥的速度越快，受到水的阻力越大，越难继续挥拳。这个水的"阻力"跟D算法的作用很像，因此可以把D算法理解为"阻尼"，抑制过冲现象。

缺点：对噪声敏感。

2.4 从数学表达式到代码

u k = K p ∗ e k + K i ∑ j = 0 k e j + K d ( e k − e k − 1 ) u_k=K_p*e_k+K_i\sum^{k}{j=0}e_j+K_d(e_k-e{k-1}) uk=Kp∗ek+Kij=0∑kej+Kd(ek−ek−1)

在keil中，用C语言实现

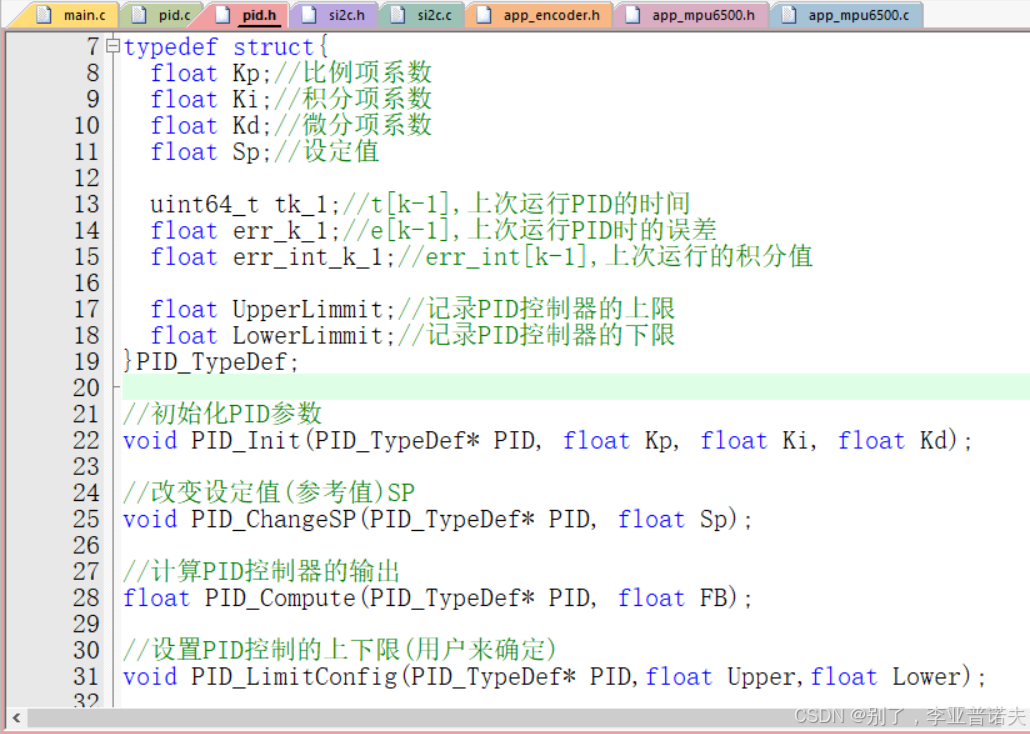
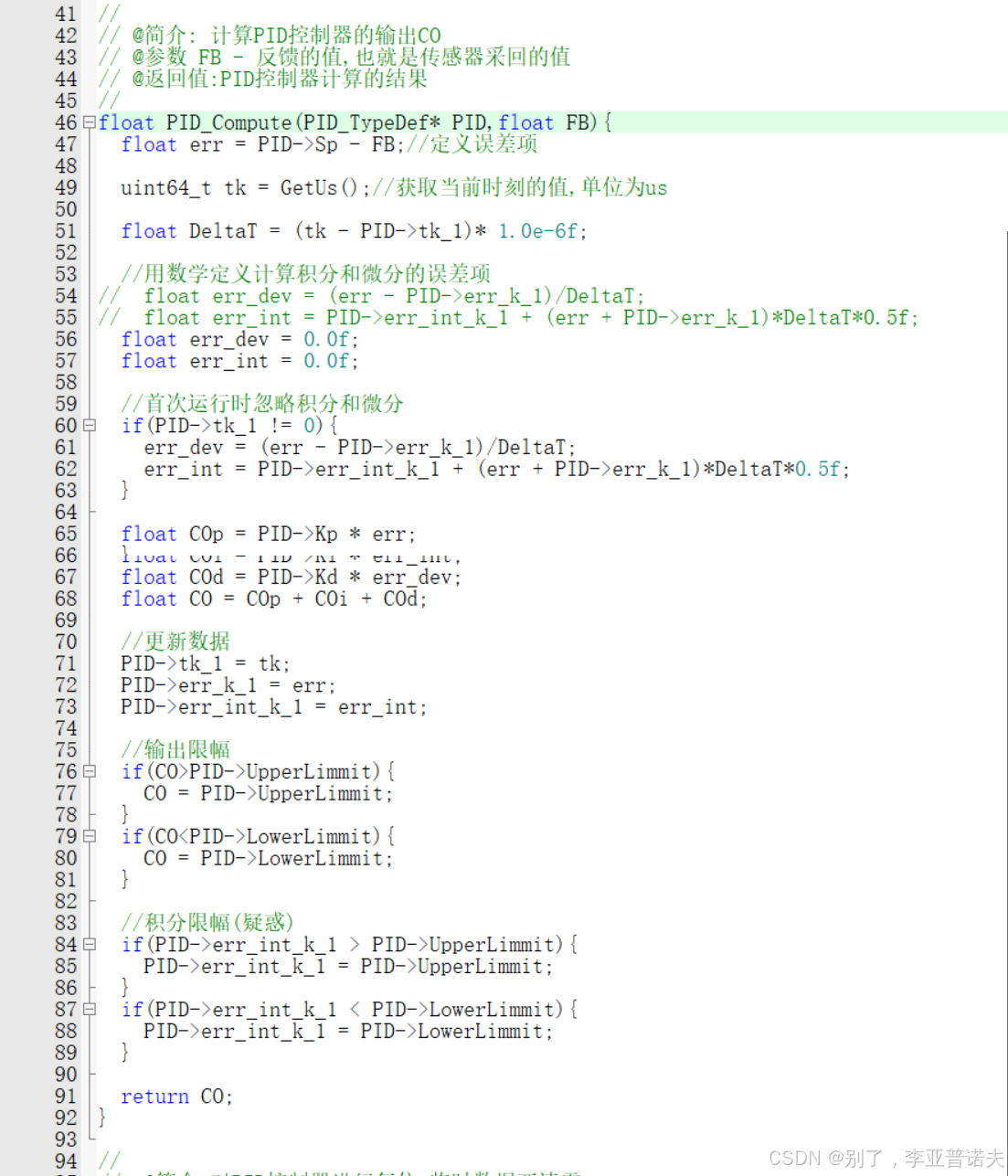
书本公式是理想的，实际写代码（C语言）时，必须处理以下问题，否则PID根本没法用：

积分饱和 ------ 必做！
现象：电机启动瞬间，误差很大，I 项迅速累加到一个天文数字。等电机到了目标速度，I 项还很大，导致电机严重超速。
对策：积分限幅，当积分累加到控制量的输入上限，停止累加。
死区控制
现象：在误差非常小（比如 1 rpm）时，系统可能会频繁微调，导致电机抖动。
对策：如果 ∣ e r r o r ∣ < 阈值 |error|<阈值 ∣error∣<阈值，则认为 e r r o r = 0 error=0 error=0，不做调节，让系统"休息"。

实际使用中PID的各类组合

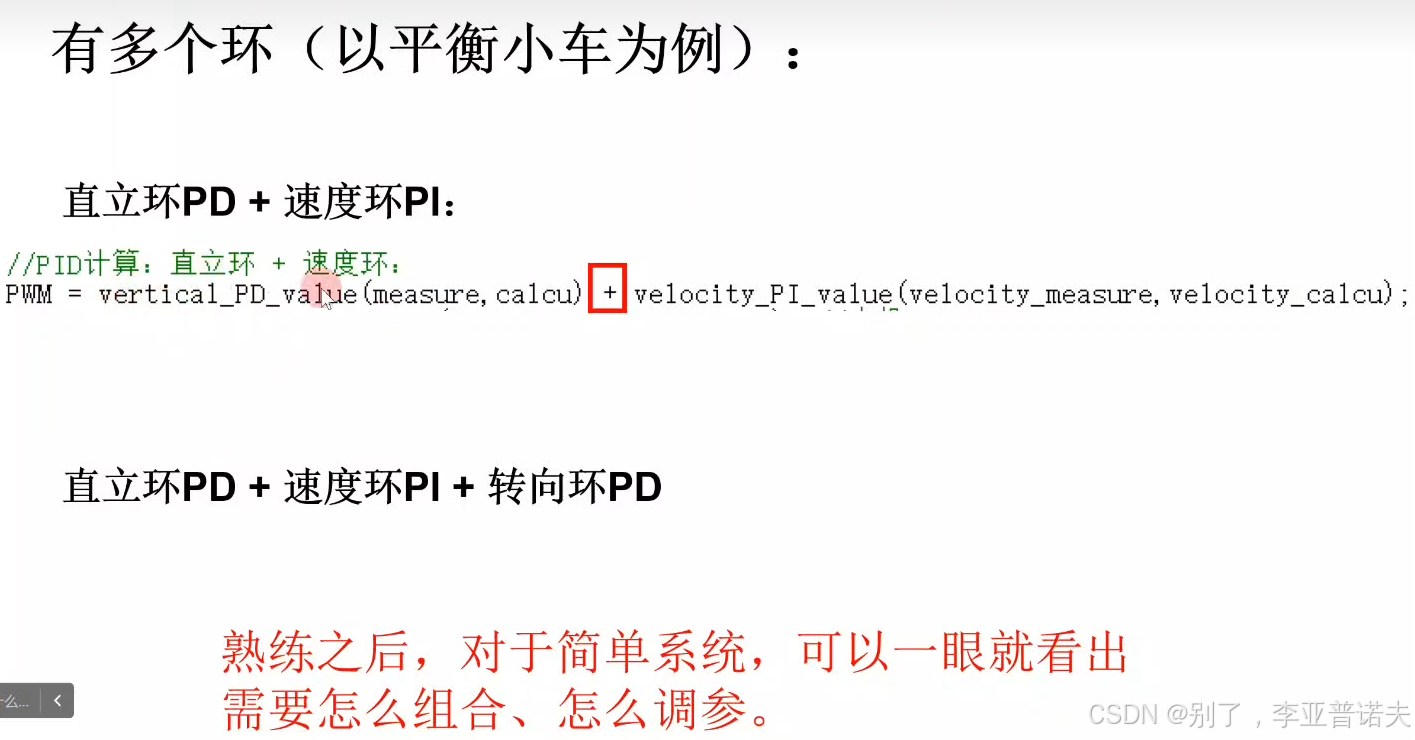
2.5 PID在电机控制中的使用

在电机控制系统（如直流调速、FOC矢量控制的速度环）中，90%以上的情况只用 PI（比例-积分），而把 D（微分）项置为0。

主要原因：

噪声放大
微分项 D D D的数学定义是 K d × d e ( t ) d t K_d \times \frac{de(t)}{dt} Kd×dtde(t)（误差的变化率）。
现实中，测速信号（M法/T法/M/T法）其实是不平滑的。编码器会有量化误差，电磁干扰会带来毛刺。
假如速度信号里混入了一个极短的高频尖峰噪声（哪怕幅值很小），它的变化率（斜率）是无穷大的。D环节一旦看到这个无穷大的斜率，就会瞬间输出一个巨大的控制电压。
系统惯性与响应需求
D是"预测未来"，它在误差刚开始变化时就猛烈介入，为了抑制超调，相当于一个"阻尼器"。
电机是典型的一阶惯性环节 （机械时间常数）。电机的机械惯性本身就起到了滤波和平滑的作用，速度一般不会发生那种"完全无法控制的突变"。
只要 P（比例）给得够，响应速度通常已经足够满足工业需求；I（积分）负责消除静差。对于速度环，不需要 D 来进行过度的"超前预测"。
甚至可能导致不稳定
电机和负载（如齿轮箱、皮带）之间存在柔性连接，这会产生机械谐振。
D 环节会增加系统的高频增益，容易正好"踩中"这个机械谐振频率，导致整个系统发生机械震荡。

极点对消（零极点配置）

直流电机的电磁惯性和机械惯性在数学上大多近似为一阶惯性环节 。

我们设计PI调节器时，用PI的"零点"去抵消电机对象的极点（那个惯性大的大滞后）

什么时候必须要用 D ？

通常在位置环或者是温度控制这种大滞后系统中。

位置环：当你要精确定位时，为了不冲过头（超调），需要 D 来充当"刹车"。

温度/化工：热惯性太大，现在的加热动作可能5分钟后才体现出来，必须用 D 提前预测趋势。

PID控制器的设计过程分两步

第一步，先选择调节器的结构，以确保系统稳定，同时满足所需的稳态精度

第二步，选择调节器的参数，以满足动态性能指标的要求

严谨的设计方法

在电力拖动自动控制系统的分析和设计中最常应用的是伯德图 ，即开环对数频率特性的渐近线，它的绘制方法简便，可以确切地提供稳定性和稳定裕度的信息，然后根据三频段理论，确定PID控制器的设计

试凑法，确定PID控制器的参数

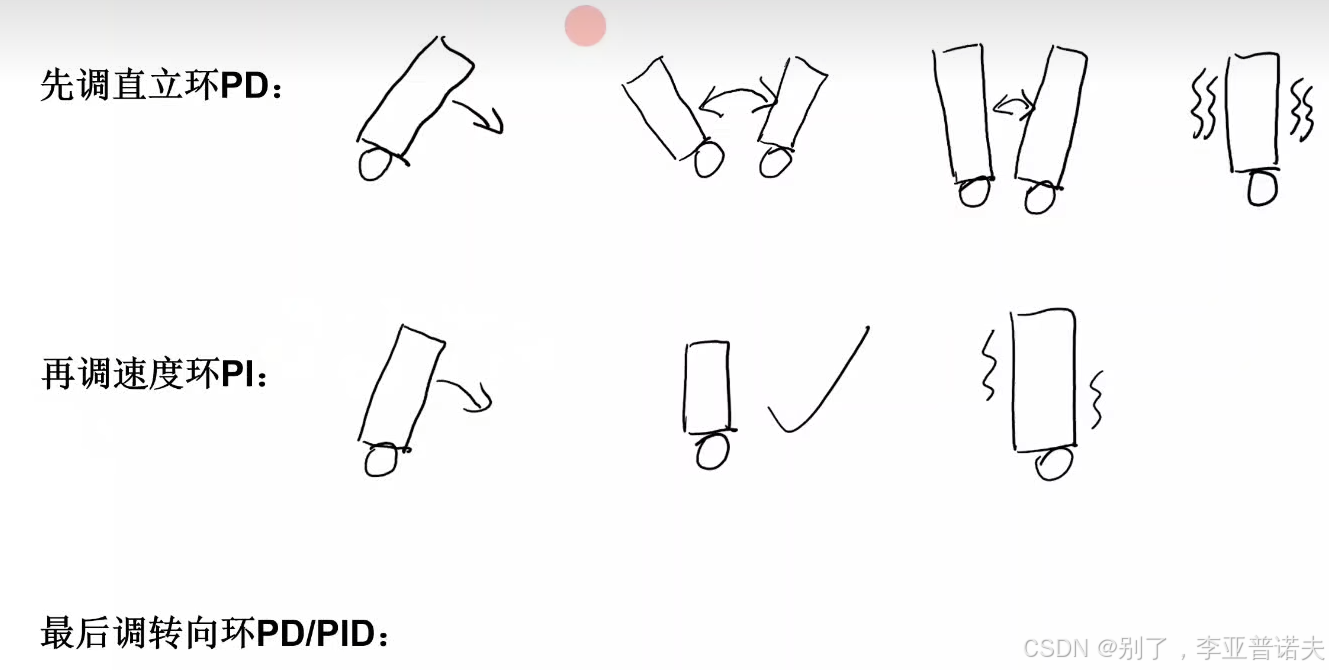
第一步：准备工作

断开I和D，设置 K p = 0 K_p=0 Kp=0， K i = 0 K_i=0 Ki=0， K d = 0 K_d=0 Kd=0

设定目标：给一个阶跃信号（比如目标转速从 0 跳变到 500 rpm）。

第二步：调 P (先快起来)

从小到大增加 K p K_p Kp

当系统开始出现轻微的震荡（嗡嗡声或波形来回晃）时，把 K P K_P KP往回调小一点（比如取当前值的 60%~70%）。

此时状态：响应挺快，但转速达不到 500，可能稳定在 480 rpm（这就是静差）。

第三步：调 I (消除误差)

保持 K p K_p Kp不变，开始一点点增加 K i K_i Ki

观察：那个 480 rpm 的实际值会慢慢爬升，最终与 500 rpm 重合。

副作用： K i K_i Ki加得越大，超调量可能越大（比如先冲到 550 再回来）。
只要静差能消除，且超调在允许范围内，I 越小越安全。

第四步：调 D (如果必须的话)

对于电机调速，这一步通常跳过。

如果系统超调太大，且无法通过减小 K i K_i Ki来解决，可以微量加入 K d K_d Kd起到刹车作用。

总结

以上为数字测速方法和PID算法的介绍，PID控制器的参数设计需要大量实践，对后续的电机控制及其重要。