1.数学模型转换
理科中很多问题会给你一段场景描述,这个场景可能直接来源生活、或者来源于某个故事,然后会提出一个问题让你解决。
例如:一个圆形蛋糕被分成 16 等份后,小明想要吃其中的 A 块,小华想要吃其中的 B 块,但是同一个人不能拿相邻的两块蛋糕。请问他们能否拿到自己想要的数量的蛋糕?
类似这种题目我们要做的第一件事情是理解题干中描述的数学问题:一个蛋糕分成 16 份,想要蛋糕不相邻,换个角度思考,不能拿超过 8 个,超过了就肯定要相邻了;一个人拿完以后,剩下那个人只剩下 8 个不相邻的可以拿,多了也没有。
这题就转换成小明和小华每人各拿不超过 8 块就行,即 A<=8 and B<=8 即可。
当然这是一个比较简单的例子。在更多场合我们需要灵活使用计算、几何、二进制、坐标系等你熟悉的数学知识,将遇到的问题与你了解的数学模型关联起来-----一个问题可能可以关联不止一个数学模型,选择合适的数学模型,能够为你解题提供最佳途径。
2.纸币组成
现有面值为4元和7元的纸币各100张。请问用这些纸币能否组成N元(N<=100)
本题数学模型转换是不定方程问题(未知数的数量超过方程的数量),即 4x+7y=n 求整数解(x、y 可以为 0)。
从效能最优角度来思考,这里可以考虑只枚举 y,只有 n-y能被 4 整除,使得 x 可以取到整数解。注意 y 可以取 0,也就是不用 7 元纸币的意思。就不用二重循环枚举了。
为了简便这里直接上 7,就不再 1*7 了
cpp
for(int y=0;y<=n;y+=7)
{
if((n-y)%4==0)
{
//有整数解
}
}3.给定一个正整数 n,请你计算在 1 和 n 之间有多少个奇数有 8 个因数(n<=200)
这个题目的方法有多种,当 n 不大时,这些方法都能行得通。
方法 1:如果1 到之间有正好 4 个数可以被 n 整除,且
不是整数,那么这个 n 刚好满足 8 个因数的条件
解读:首先如果是整数,说存在整数 k=
,满足 k*k=n,这样 n 的因数一定是奇数个(那就不是 8 了);其次既然
左侧(比
小)有 4 个因数,说明与这 4 个因素存在一一对应的 4 个更大的因数在
右侧(因数都是一对对的出现)
方法 2:对 n 进行质因数分解。

8=4*2=2*2*2
也就是说这个 n 可以是 或者
的形式 (质因数的分解在往期的初级算法技巧有总结)
【更复杂的思考】:如果 n 很大,最大可以到,应该如何处理这个问题?
首先方法 1 是必然超时的:其时间复杂度是*
,已经超过了
的安全上限,这个做法必然拿不到全分。
方法 2 需要进行一些调整:如果对于每个数 i 我们都是用"现做"的方式去分解质因数----对每个数的因数都是从 2 到 开始尝试进行分解,速度会要比方法 1 快一些(因为每找到一个)n 就要除掉这个因素,自身会缩小。
但是仍然有极端情况:如果某个 i 是个质数,且其大小接近,对这个 i 就可能超时!导致程序本身超时。
所以这里有一种做法,但是需要我们学完数组以后才能做:
既然 n 最大,首先枚举
以内的质数放在数组里,然后在质因数分级的时候只要尝试这些质数就可以----这样可以大幅降低计算次数,使得在 n 很大的时候都不会超时。
总结:
一个题目可能有多个解法,但是在某些条件限制以后(如数据上限),这会导致一些原本可行的方法超时,需要谨慎的选择更合适的算法。
4.画空心菱形

从示例可以看出,当 n=3 时,输出了一个 5 层的菱形,这里讲两种绘制方法:
【使用模拟绘制】:
模拟法是一种通用的技法,如果我们没有办法总结归纳更好的办法时,模拟法是一种"寻求问题自然解"的做法:通过直观的描述这个事情怎么做,从而求解。
这种做没有算法上的难度,但是本题逻辑比较复杂,也是大家第一次接触到这种不难但是过程长、代码长的题目。
此题型主要考察对问题的理解是否全面、考虑是否周到、能否构建完全匹配问题的思维模式,不能遗漏。
这个菱形一共有 2n-1 层,并且以第 n 层为分界,从 1 到第 n 层逐渐变宽、从第 n 层到第 2n-层逐渐收拢
对于每一层来说共有4 个操作动作:
1.前空格
2.画*
3.中间空格
4.画*
其中第 1 层和第 2n-1 层例外,只有步骤 1、2,没有 3、4
观察前空格和中空格的数量:
以 n=3 为例
每层前空格的数量为:2 1 0 1 2
每层中间空格的数量为: 0 1 3 1 0
如果扩展到 n=4:
每层前空格的数量为:3 2 1 0 1 2 3
每层中间空格的数量为: 0 1 3 5 3 1 0
推理公式:其中 i 为行数(虽然题目只给了一个例子,但是我们需要扩展多个例子总结规律)
前空格: n-1 n-2 .... 0 1 2...n-2 n-1 ,让 i 从 1 开始,每一行输出的空格数量就是 n-i 。到第 n 行正好输出 0 个前空格
中空格: 0 1 3 .. 2(n-1)-1 2(n-1)-3 ... 3 1 0 ,让 i 从 1 开始, 每一行输出的中空格数量就是 2(n-i)-1, 注意 i 等于 1 时,这个值为-1,可以理解为不输出中空格
因为 1-n 是增长,n 到 2n-1 是下降,为了方便理解,这里可以把菱形拆成上下两部分输出,也就是由两个循环来处理。
大致的代码:
上半段的循环:
处理前空格的循环
输出*
处理中空格的循环。注意特判一层,第一层没有中空格和输出,在这一层要 continue
输出*
下半段的循环:
处理前空格的循环
输出*
处理中空格的循环 注意特判第 2n-1 层,没有中空格和输出
输出*
【捷径】
一般来说做起来比较复杂的题目都可能存在捷径。捷径需要你充分观察和理解题目,重绘数学模型,从而在高一个维度推演出来更简便的思路。
是的,所谓捷径,通常都是在高一个认知维度的降维打击。
站在盘外思考:
对于输入 n 来说,我们实际上绘制了了 (2n-1)*(2n-1)个格子,每个格子不是*就是空格
菱形是一个轴对称图形,这个题目给出的菱形是左右对称的,其中轴线正好是第 n 列,其菱形的中心点就是(n,n)。
当 n=5 时,如下图,C 是中心点,正好在(5,5)的位置。
|----|----|----|----|----|----|----|----|----|
| | | | | * | | | | |
| | | | * | | * | | | |
| | | * | | | | * | | |
| | * | | | | | | * | |
| * | | | | C | | | | * |
| | * | | | | | | * | |
| | | * | | | | * | | |
| | | | * | | * | | | |
| | | | | * | | | | |
对于每一个*,注意*的横坐标和纵坐标(左上角从 1,1 开始), 这个点对于中心点 (n,n)的横坐标和纵坐标的差值正好是 n-1,即dx-n 的绝对值和 dy-n 的绝对值之和正好就是 n-1。(观察总结)
满足这个条件就输出*,其他时候就输出空格。
如此一来这个问题简化很多了:
cpp
int n;
cin>>n;
for(int x=1;x<=2*n-1;x++)
{
for(int y=1;y<=2*n-1;y++)
{
if(abs(x-n)+abs(y-n)==n-1)
cout<<"*";
else
cout<<" ";
}
}总结:观察角度的不同,决定了这个题目的复杂度。
模拟法可以帮你兜底,但不一定是最好的做法。更好的做法要看你对题目的理解程度和动手程度,信息学竞赛要求我们善于观察和发现规律,在学习信息学竞赛的过程中这两种能力也会得到充分锻炼。
5.二进制转十进制
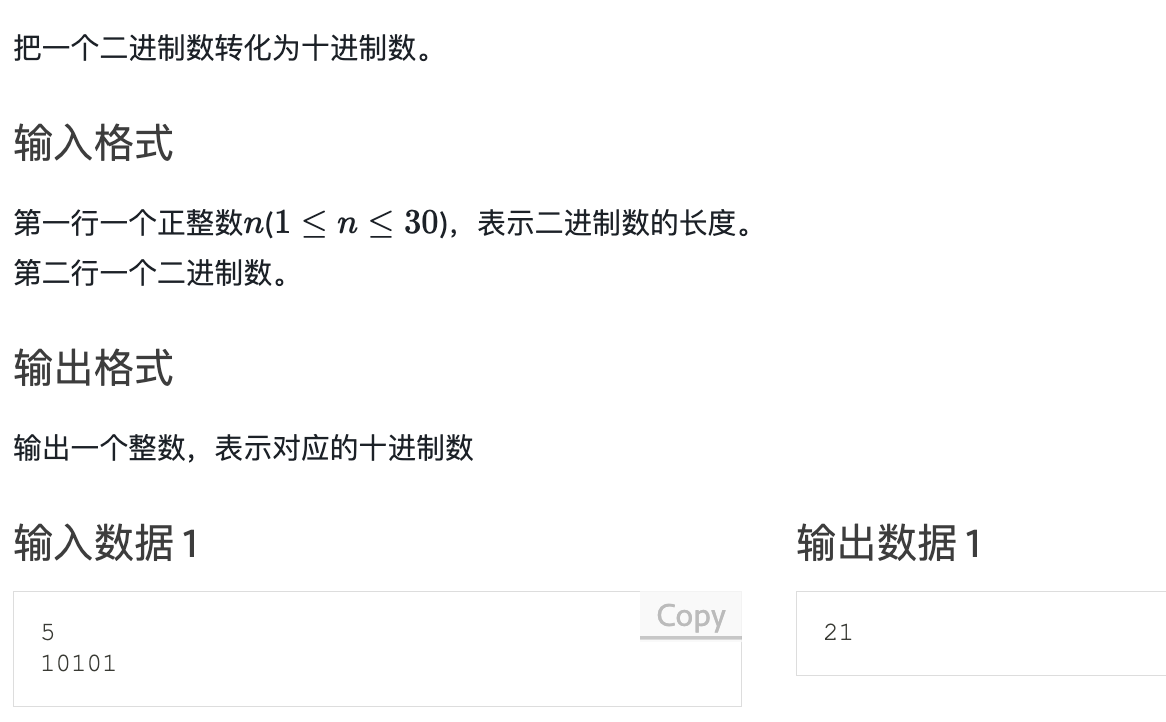
我们目前的进度讲完了二进制但是还没有讲到数组和 string,且已经知晓 n 最多有 30 位,所以用 longlong 都是没有办法完整的接收 n 的。所以要另想办法。
对于一个二进制数例如:10101,其转换为十进制的规则为:
我们事先已经从题目知道了这个二进制有 n 位,这就方便我们处理了:这里可以在循环中用 char 读取二进制的每一位,比对当前的值,乘以二进制的权即可。
cpp
int a;
char b;
cin>>a;
int q= 1<<(a-1); //通过位移预算直接得到最高位的权
int sum=0;
for(int i=0;i<a;i++)
{
cin>>b;
if(b=='1')
sum+= q;
q>>=1;//位权降低 1,效果等同于 /2
}
cout<<sum;总结:
办法总比困难多,灵活运用现有的知识来帮助你解决问题。
6.四舍五入是一种常见的近似计算方法。现在,给定 n 个整数,你需要将每个整数四舍五入到最接近的整十数。例如,43 四舍五入后为 40,58 四舍五入后为 60。
C++中当然是没有现成的可以将整数四舍五入的方法的。
所以本题我们看思考这个四舍五入的本质:
当最后一位大于等于 5,那么十位就要加 1,否则十位不加,然后最后一位需要抹除。
那么我们要做的事情:
1.用%拿到个位a
2.将输入的数据 /10 再 *10,这样通过整除的特性抹掉了最后一位
3.判断a 的大小,如果大于等于 5,则第二步得到的数据+10
输出结果。
总结:当要做的事情无法一步到达时,拆解步骤,看看每一步是否都可以实现,那就整件事可以实现。
7."考虑无序对" 或 "不计顺序的有序对" 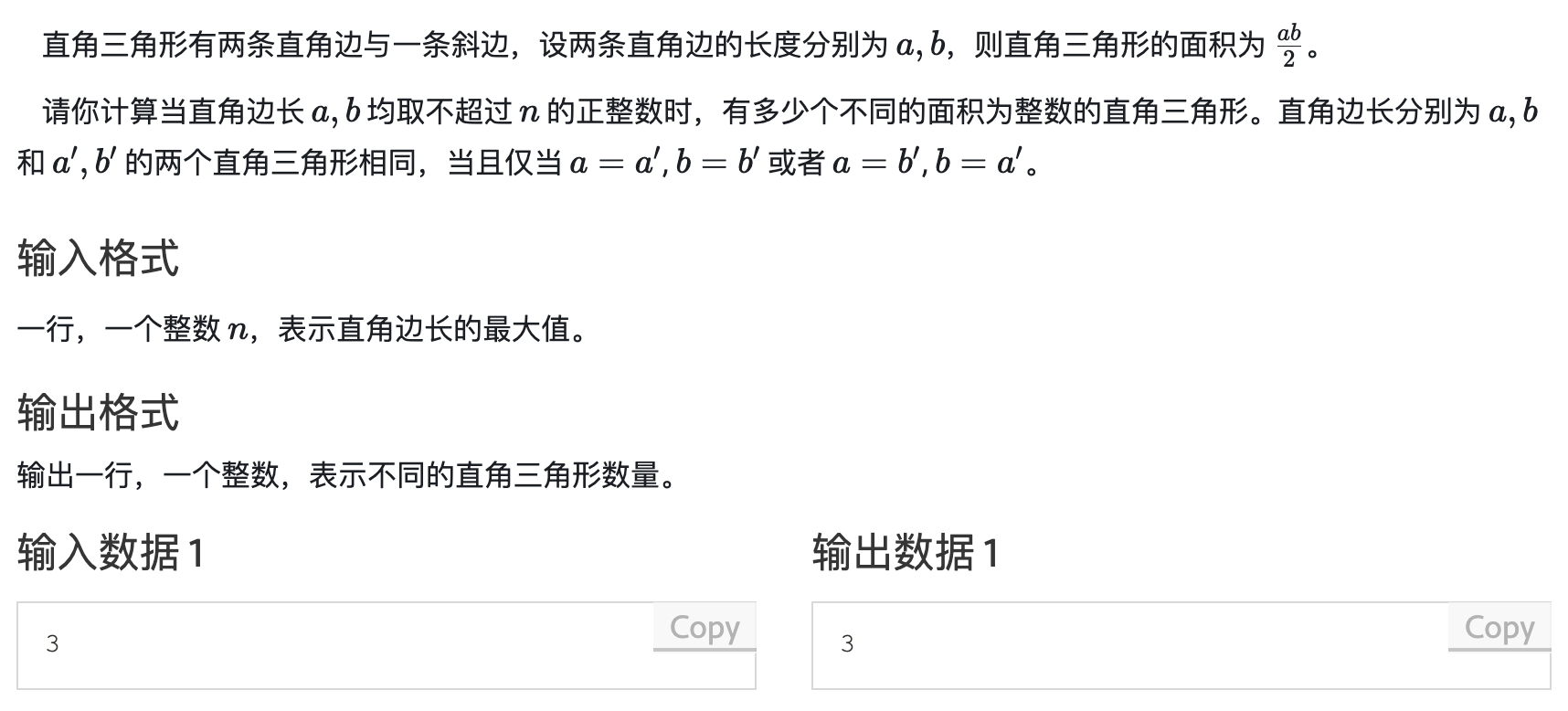
本题的数学模型实际上是直角三角形面积的整数解,这就要求两条边的至少有一个为偶数(这样才能确保a*b的结果可以被2整除,使得结果为整数),解决这个问题依靠枚举即可,a和b都是从1枚举到n,然后判断a和b是否至少有一个能整除2即可。
但是本题有一个附件条件:那就是当a和b调换以后,认为这是一个重复的三角形(不能重复计入次数)
那么这一题就要在a和b至少有一个偶数的基础上,只能计算"有序对"的ab(即如出现先a后b的情况,则不取先b后a)
本题其实有一个非常好的参考样例:99乘法表

以3*4举例,这个表是看不到4*3的
仔细观察乘法表,这个表都是 x*y=c的形式,我们可以看到这里的y都不小于x,即y>=x
应用同样的思路,我们可以来处理这个问题:
cpp
int cnt=0;
for(int a=1;a<=n; a++)
{
for(int b=a;b<=n;b++)
//关键点:b从a开始,从而确保b>=a
{
if(a%2==0 || b%2==0)
cnt++;
}
}我们让第二轮循环b从第一轮循环的当前值开始,这样就完美的避开b<a的情形,所有符合条件的ab对都满足a<=b,确保ab对不会重复。
总结:
这种循环控制的方式是常见过滤无序对的技巧,在要求多个变量保持从小到大的关系是,也可以参考这个思路。例如:a、b、c三个数的和不超过n,要求a<b<c,求a、b、c的正整数解的数量,就可以使用这个思路。
8.幂和数

直观做法:如果直接使用2的n次方去暴力枚举,在n很大的时候必然会超时。
本题如果要使用更高效的解法,首先要明确对n的认知。
既然n可以表示为2个由2的若干次方的和,那么的n的二进制一定能表达为以下形式:
000000000000000000000000000110000
上述2进制数一定只有不超过2个1
解读:
题目没有明确x和y是否相同,这里分情况讨论:
1.当x和y相同时,原式可以表达为,很明显,此时n的二进制只有1个1
2.当x和y不同时,和
各占据一个1,此时n的二进制有2个1
所以本题的实质就是检测l和r之间所有数,看看这些数的二进制中有多少个数含有1的个数不超过2
cpp
int cnt=0;
for(int i=l;i<=r;i++)
{
int t=i;//一定要暂存一个t用来计算,因为i是不能变的
int cnt2=0;
while(t)
{
if(t%2==1) // 可以替换为 t&1==1 ,其意义为通过与运算判断最低位是否为1,和当前等效
cnt2++;
t>>1;//右位移,等效 t/=2,但是速度更快
}
if(cnt2<=2)
cnt++;
}总结:
一题虽然可能多解,但是必然有1种思路是最契合题目设计意图的,这个思路通常来说是最优解。