一、代码完整实现
python
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
class Kinematics:
def __init__(self):
"""初始化运动学模块,使用JAKA Zu12官方DH参数"""
# JAKA Zu12 D-H 参数表(单位:mm,角度:rad)
# 标准DH参数定义:[a_i, alpha_i, d_i, theta_i]
# a: 连杆长度(沿x_i方向)
# alpha: 连杆扭转角(绕x_i旋转)
# d: 连杆偏移(沿z_{i-1}方向)
# theta: 关节角(绕z_{i-1}旋转)
self.dh_params = [
[0.0, 0.0, 142.65, 0.0], # 关节1:基座旋转
[0.0, np.pi/2, 0.0, 0.0], # 关节2:肩部俯仰
[595.0, 0.0, 0.0, 0.0], # 关节3:肘部伸展
[571.5, 0.0, -131.5, 0.0], # 关节4:腕部旋转
[0.0, np.pi/2, 115.0, 0.0], # 关节5:腕部俯仰
[0.0, -np.pi/2, 103.5, 0.0] # 关节6:末端工具旋转
]
def compute_transformation_matrix(self, a, alpha, d, theta):
"""计算单个关节的齐次变换矩阵(标准DH约定)"""
ctheta = np.cos(theta)
stheta = np.sin(theta)
calpha = np.cos(alpha)
salpha = np.sin(alpha)
# 标准DH变换矩阵(4步变换组合)
T = np.array([
[ctheta, -stheta * calpha, stheta * salpha, a * ctheta],
[stheta, ctheta * calpha, -ctheta * salpha, a * stheta],
[0.0, salpha, calpha, d],
[0.0, 0.0, 0.0, 1.0]
])
return T
def forward_kinematics(self, joint_values):
"""正运动学:关节角度 → 末端位姿(位置+姿态)"""
if len(joint_values) != 6:
raise ValueError("JAKA Zu12为6轴机械臂,需提供6个关节角度")
# 累积变换:T0_6 = T0_1 * T1_2 * ... * T5_6
T = np.eye(4)
for i in range(6):
a, alpha, d, theta_offset = self.dh_params[i]
theta = theta_offset + joint_values[i] # 关节变量叠加
T_i = self.compute_transformation_matrix(a, alpha, d, theta)
T = np.dot(T, T_i)
# 提取位置向量 (x, y, z)
position = T[:3, 3]
# 提取旋转矩阵 (3x3)
R = T[:3, :3]
# 旋转矩阵 → 欧拉角(Z-Y-X,即RPY:Roll-Pitch-Yaw)
# 注意:存在万向节死锁问题(当pitch=±90°时)
if abs(R[0, 2]) >= 1:
# 万向节死锁处理
ry = np.sign(R[0, 2]) * np.pi/2
rx = 0
rz = np.arctan2(-R[1, 0], R[1, 1])
else:
ry = np.arcsin(R[0, 2])
rx = np.arctan2(-R[1, 2], R[2, 2])
rz = np.arctan2(-R[0, 1], R[0, 0])
return {
'x': position[0], 'y': position[1], 'z': position[2],
'rx': rx, 'ry': ry, 'rz': rz, # 单位:弧度
'rotation_matrix': R,
'transformation_matrix': T
}
def inverse_kinematics(self, pose, elbow_up=True):
"""
逆运动学:末端位姿 → 关节角度(含肘部配置选择)
参数:
pose: {'x','y','z','rx','ry','rz'} 末端位姿
elbow_up: True=肘部向上配置, False=肘部向下配置
返回:
joints: [q1,q2,q3,q4,q5,q6] 关节角度列表(弧度)
"""
# 1. 位姿预处理
x, y, z = pose['x'], pose['y'], pose['z']
rx, ry, rz = pose['rx'], pose['ry'], pose['rz']
R = self.euler_to_rotation_matrix(rx, ry, rz)
# 2. 计算腕部中心(Wrist Center)
# 末端到法兰距离 = d5 + d6(沿工具Z轴方向)
d5 = self.dh_params[4][2] # 115.0 mm
d6 = self.dh_params[5][2] # 103.5 mm
tool_offset = d5 + d6
# 从末端位姿反推腕部中心
a_x, a_y, a_z = R[:, 2] # 旋转矩阵第三列为Z轴方向
wx = x - tool_offset * a_x
wy = y - tool_offset * a_y
wz = z - tool_offset * a_z
# 3. 求解关节1(基座旋转角)
# 投影到XY平面,atan2处理全象限
q1 = np.arctan2(wy, wx)
# 4. 求解关节2和3(平面2R机构)
d1 = self.dh_params[0][2] # 142.65 mm (基座高度)
a3 = self.dh_params[2][0] # 595.0 mm (连杆3长度)
a4 = self.dh_params[3][0] # 571.5 mm (连杆4长度)
d4 = self.dh_params[3][2] # -131.5 mm (连杆4偏移)
# 转换到关节1坐标系(绕Z轴旋转-q1)
wx_prime = wx * np.cos(q1) + wy * np.sin(q1)
wy_prime = wz - d1
# 计算三角形边长
r = np.sqrt(wx_prime**2 + wy_prime**2)
# 余弦定理求关节3角度(肘部配置选择)
cos_q3 = (wx_prime**2 + wy_prime**2 + a3**2 - a4**2) / (2 * a3 * r)
if abs(cos_q3) > 1.0:
raise ValueError(f"目标点超出工作空间范围: cos(q3)={cos_q3:.3f}")
sin_q3 = np.sqrt(1 - cos_q3**2)
q3 = np.arctan2(sin_q3 if elbow_up else -sin_q3, cos_q3)
# 求解关节2
theta23 = np.arctan2(wy_prime, wx_prime)
q2 = theta23 - q3 - np.pi/2 # 注意:JAKA Zu12关节2零位定义特殊
# 5. 求解腕部关节4/5/6(姿态解耦)
# 计算T0_3(基座到连杆3末端)
T01 = self.compute_transformation_matrix(*self.dh_params[0][:3], q1)
T12 = self.compute_transformation_matrix(*self.dh_params[1][:3], q2)
T23 = self.compute_transformation_matrix(*self.dh_params[2][:3], q3)
T03 = T01 @ T12 @ T23
# 计算T3_6(连杆3到末端)
T06 = np.eye(4)
T06[:3, :3] = R
T06[:3, 3] = [x, y, z]
T36 = np.linalg.inv(T03) @ T06
# 从T3_6提取腕部关节角
q5 = np.arctan2(np.sqrt(T36[0, 2]**2 + T36[1, 2]**2), T36[2, 2])
# 处理奇异位形(q5 ≈ 0)
if abs(np.sin(q5)) < 1e-6:
q4 = 0 # 任意值,此处设为0
q6 = np.arctan2(-T36[1, 0], T36[0, 0]) - q4
else:
q4 = np.arctan2(T36[1, 2], T36[0, 2])
q6 = np.arctan2(-T36[2, 1], T36[2, 0])
return [q1, q2, q3, q4, q5, q6]
def euler_to_rotation_matrix(self, rx, ry, rz):
"""欧拉角(Z-Y-X)→ 旋转矩阵"""
# 绕X轴旋转(Roll)
Rx = np.array([
[1, 0, 0],
[0, np.cos(rx), -np.sin(rx)],
[0, np.sin(rx), np.cos(rx)]
])
# 绕Y轴旋转(Pitch)
Ry = np.array([
[ np.cos(ry), 0, np.sin(ry)],
[ 0, 1, 0 ],
[-np.sin(ry), 0, np.cos(ry)]
])
# 绕Z轴旋转(Yaw)
Rz = np.array([
[np.cos(rz), -np.sin(rz), 0],
[np.sin(rz), np.cos(rz), 0],
[0, 0, 1]
])
# 复合旋转:R = Rz * Ry * Rx(注意顺序!)
return Rz @ Ry @ Rx
def rotation_matrix_to_euler(self, R):
"""旋转矩阵 → 欧拉角(Z-Y-X)"""
if abs(R[0, 2]) >= 1:
ry = np.sign(R[0, 2]) * np.pi/2
rx = 0
rz = np.arctan2(-R[1, 0], R[1, 1])
else:
ry = np.arcsin(R[0, 2])
rx = np.arctan2(-R[1, 2], R[2, 2])
rz = np.arctan2(-R[0, 1], R[0, 0])
return rx, ry, rz
def visualize_robot(self, joint_angles, ax=None):
"""可视化机械臂构型(需matplotlib 3D支持)"""
if ax is None:
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# 计算各关节位置
positions = [[0, 0, 0]] # 基座原点
T = np.eye(4)
for i in range(6):
a, alpha, d, theta_offset = self.dh_params[i]
theta = theta_offset + joint_angles[i]
T_i = self.compute_transformation_matrix(a, alpha, d, theta)
T = T @ T_i
positions.append(T[:3, 3].tolist())
# 绘制连杆
xs, ys, zs = zip(*positions)
ax.plot(xs, ys, zs, 'o-', linewidth=3, markersize=8, color='blue')
# 设置坐标轴
ax.set_xlabel('X (mm)', fontsize=12)
ax.set_ylabel('Y (mm)', fontsize=12)
ax.set_zlabel('Z (mm)', fontsize=12)
ax.set_title('JAKA Zu12 机械臂构型', fontsize=14, fontweight='bold')
ax.grid(True)
ax.set_box_aspect([1,1,1]) # 等比例缩放
# 设置工作空间范围(JAKA Zu12臂展1327mm)
max_range = 1400
ax.set_xlim([-max_range, max_range])
ax.set_ylim([-max_range, max_range])
ax.set_zlim([0, max_range])
plt.tight_layout()
return ax二、核心算法原理深度解析
2.1 DH参数建模:机械臂的"骨骼系统"
标准DH参数四要素
| 参数 | 物理意义 | JAKA Zu12典型值 | 作用 |
|---|---|---|---|
| a_i | 连杆长度 | 595mm (关节3) | 沿x_i轴的平移 |
| α_i | 扭转角 | 90° (关节2) | 绕x_i轴的旋转 |
| d_i | 偏移量 | 142.65mm (关节1) | 沿z_{i-1}轴的平移 |
| θ_i | 关节角 | 变量 | 绕z_{i-1}轴的旋转 |
关键理解 :DH参数本质是相邻坐标系间的变换规则。每个关节对应一个4×4齐次变换矩阵,6个关节串联形成从基座到末端的完整变换链。
JAKA Zu12 坐标系布局示意图
python
基座坐标系 {0}
│
├── 关节1 (θ1):绕Z0旋转 → 坐标系{1}
│ (a1=0, α1=0, d1=142.65)
│
├── 关节2 (θ2):绕Z1旋转 → 坐标系{2}
│ (a2=0, α2=90°, d2=0) ← 扭转90°使Z2指向水平
│
├── 关节3 (θ3):绕Z2旋转 → 坐标系{3}
│ (a3=595, α3=0, d3=0) ← 主臂伸展
│
├── 关节4 (θ4):绕Z3旋转 → 坐标系{4}
│ (a4=571.5, α4=0, d4=-131.5) ← 腕部偏移
│
├── 关节5 (θ5):绕Z4旋转 → 坐标系{5}
│ (a5=0, α5=90°, d5=115)
│
└── 关节6 (θ6):绕Z5旋转 → 末端坐标系{6}
(a6=0, α6=-90°, d6=103.5)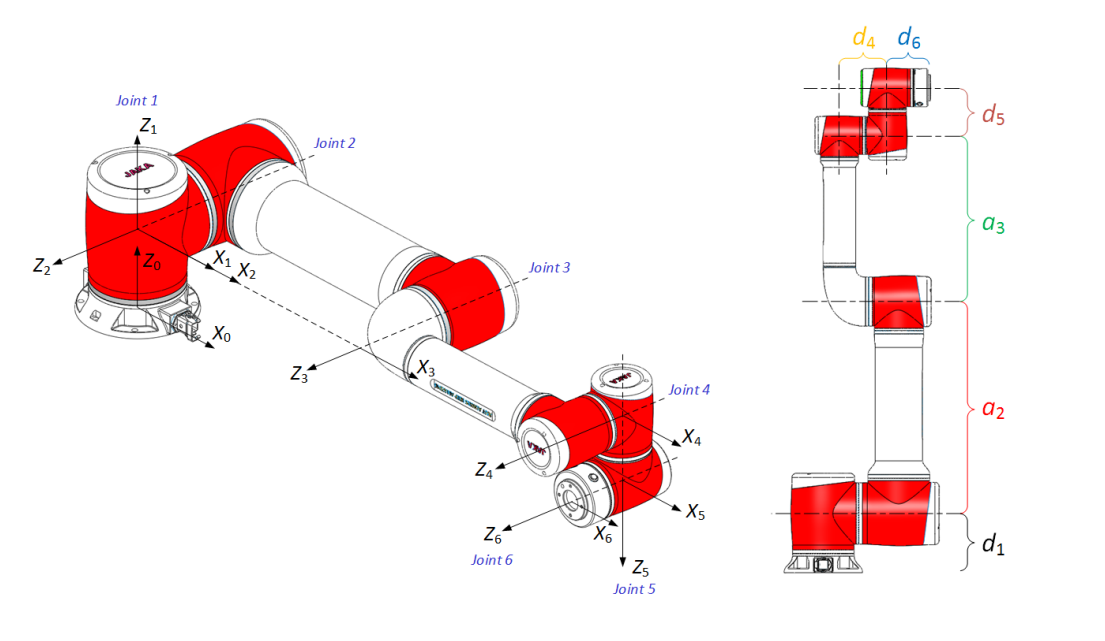
使用的是JAKA的资料图片,侵权删除
工程提示:JAKA Zu12的d4为负值(-131.5mm),表示腕部存在向下偏移,这是避免与工件干涉的关键设计。
2.2 正运动学:从"关节角度"到"末端位姿"
算法流程(6步链式变换)

数学本质
末端位姿由4×4齐次变换矩阵完整描述:
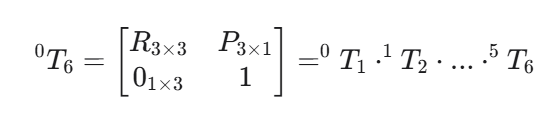
其中:
- R:3×3旋转矩阵,描述末端朝向
- P:3×1位置向量,描述末端位置
代码关键点
python
# 累积变换(矩阵连乘)
T = np.eye(4) # 单位矩阵初始化
for i in range(6):
T_i = compute_DH_matrix(...) # 单关节变换
T = T @ T_i # 注意顺序:左乘(标准DH约定)⚠️ 常见错误:矩阵乘法顺序错误(应为T = T @ T_i,而非T = T_i @ T),这会导致坐标系变换方向颠倒。
2.3 逆运动学:从"末端位姿"到"关节角度"
解耦法(Pieper条件):6轴机械臂的优雅解法
JAKA Zu12满足Pieper条件(最后3个关节轴线交于一点),可将逆解分解为:
- 位置解:前3个关节 → 确定腕部中心位置
- 姿态解:后3个关节 → 确定末端朝向
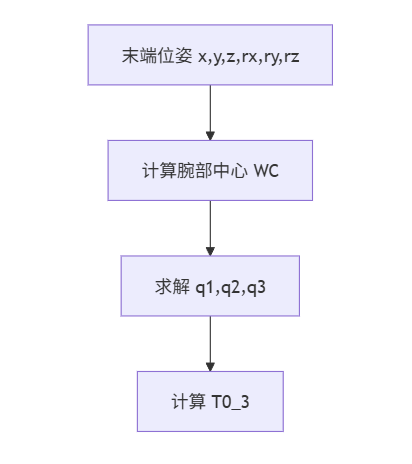
步骤1:腕部中心计算
python
# 末端Z轴方向(工具坐标系)
a = R[:, 2] # 旋转矩阵第三列
# 腕部中心 = 末端位置 - 工具长度 × Z轴方向
WC = [x, y, z] - (d5 + d6) * a步骤2:关节1求解(基座旋转)
python
q1 = atan2(WC_y, WC_x) # 投影到XY平面几何意义:关节1仅影响腕部中心在XY平面的投影角度,与高度无关。
步骤3:关节2/3求解(平面2R机构)
将问题降维到XZ平面:
python
腕部中心 WC
*
/ \
/ \ a4=571.5
/ q3 \
*-------*
基座投影 连杆3末端
|
| d1=142.65
*
基座原点使用余弦定理:
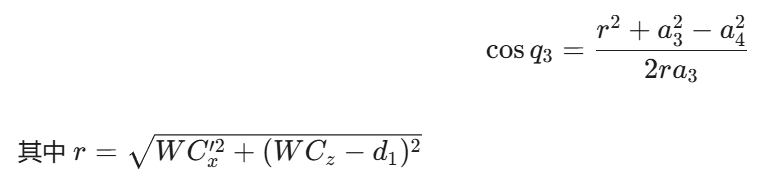
肘部配置 :sin q3 取正/负对应肘部向上/向下两种解,实际应用中需根据避障需求选择。
步骤4:腕部关节4/5/6求解
通过矩阵分解:
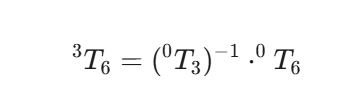

奇异位形警告:当 q5=0°q5=0° 时(腕部完全伸直),q4q4 和 q6q6 耦合,存在无穷多解,需特殊处理。
三、可视化方案
3.1 机械臂3D构型可视化
python
# 示例:绘制JAKA Zu12在特定姿态下的构型
kin = Kinematics()
# 示例关节角度(弧度):展开姿态
joints = [0, -np.pi/4, np.pi/4, 0, np.pi/4, 0]
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')
kin.visualize_robot(joints, ax)
# 添加工作空间球体(半径1327mm)
u, v = np.mgrid[0:2*np.pi:20j, 0:np.pi:10j]
r = 1327
x = r * np.cos(u) * np.sin(v)
y = r * np.sin(u) * np.sin(v)
z = r * np.cos(v)
ax.plot_wireframe(x, y, z, color="gray", alpha=0.1)
plt.show()3.2 运动学验证:正逆解一致性测试
python
# 随机关节角度
q_original = [0.5, -0.3, 0.8, -0.2, 0.4, 0.1]
# 正运动学
pose = kin.forward_kinematics(q_original)
print("末端位置: ({:.2f}, {:.2f}, {:.2f}) mm".format(
pose['x'], pose['y'], pose['z']))
# 逆运动学
q_solved = kin.inverse_kinematics(pose)
# 验证误差
error = np.max(np.abs(np.array(q_original) - np.array(q_solved)))
print(f"关节角度最大误差: {error*180/np.pi:.4f}°")3.3 工作空间可视化(蒙特卡洛法)
python
def plot_workspace(kin, samples=5000):
"""绘制JAKA Zu12可达工作空间"""
positions = []
for _ in range(samples):
# 随机生成关节角度(考虑关节限位)
q = [
np.random.uniform(-np.pi*1.5, np.pi*1.5), # ±270°
np.random.uniform(-1.48, 4.63), # -85°~+265°
np.random.uniform(-3.14, 3.14),
np.random.uniform(-3.14, 3.14),
np.random.uniform(-3.14, 3.14),
np.random.uniform(-3.14, 3.14)
]
try:
pose = kin.forward_kinematics(q)
positions.append([pose['x'], pose['y'], pose['z']])
except:
continue
positions = np.array(positions)
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(positions[:,0], positions[:,1], positions[:,2],
s=1, alpha=0.3, c='blue')
ax.set_xlabel('X (mm)')
ax.set_ylabel('Y (mm)')
ax.set_zlabel('Z (mm)')
ax.set_title('JAKA Zu12 工作空间(蒙特卡洛采样)')
plt.show()四、工程应用关键问题
4.1 奇异位形处理
| 奇异类型 | 条件 | 影响 | 解决方案 |
|---|---|---|---|
| 腕部奇异 | q5 ≈ 0° | q4/q6耦合,逆解不稳定 | 限制q5范围(如 |
| 肩部奇异 | 腕部中心在Z0轴上 | q1不确定 | 保持q1连续性(增量规划) |
| 肘部奇异 | 连杆共线 | 2R机构退化 | 避免完全伸展/折叠 |
4.2 多解选择策略
JAKA Zu12逆解通常有8组解(2^3):
- 肘部配置:2种(up/down)
- 腕部翻转:2种(flip/non-flip)
- 基座旋转:2种(±180°等效)
工程选择原则:
python
def select_best_solution(all_solutions, current_joints, obstacles=None):
"""
选择最优逆解
策略:1. 关节行程最小 2. 避开奇异位形 3. 避障
"""
best = None
min_cost = float('inf')
for sol in all_solutions:
# 成本函数:关节变化量 + 奇异惩罚
cost = np.sum((np.array(sol) - np.array(current_joints))**2)
# 奇异惩罚(当|q5|<10°时)
if abs(sol[4]) < np.deg2rad(10):
cost += 1000
if cost < min_cost:
min_cost = cost
best = sol
return best4.3 与JAKA控制器的接口
python
# 实际工程中需注意单位转换
def joints_to_degrees(joints_rad):
"""弧度→角度(JAKA API要求)"""
return [q * 180/np.pi for q in joints_rad]
def pose_from_jaka(jaka_pose):
"""JAKA位姿格式转换(X,Y,Z,Rx,Ry,Rz)"""
return {
'x': jaka_pose[0],
'y': jaka_pose[1],
'z': jaka_pose[2],
'rx': np.deg2rad(jaka_pose[3]),
'ry': np.deg2rad(jaka_pose[4]),
'rz': np.deg2rad(jaka_pose[5])
}五、算法验证与调试建议
5.1 单元测试用例
python
def test_kinematics():
kin = Kinematics()
# 测试1:零位姿
q0 = [0]*6
pose0 = kin.forward_kinematics(q0)
assert abs(pose0['x']) < 1e-6
assert abs(pose0['y']) < 1e-6
assert abs(pose0['z'] - 1426.65) < 1e-6 # 理论高度
# 测试2:正逆解一致性
q_test = [0.5, -0.3, 0.8, -0.2, 0.4, 0.1]
pose = kin.forward_kinematics(q_test)
q_inv = kin.inverse_kinematics(pose)
error = np.max(np.abs(np.array(q_test) - np.array(q_inv)))
assert error < 1e-6, f"逆解误差过大: {error}"
print("✓ 所有测试通过")5.2 常见问题排查表
| 现象 | 可能原因 | 解决方案 |
|---|---|---|
| 逆解返回None | 目标点超出工作空间 | 检查 cos_q3 是否 >1 |
| 末端抖动 | 奇异位形附近 | 限制关节5范围 |
| 姿态偏差大 | 欧拉角万向节死锁 | 改用四元数表示姿态 |
| 计算速度慢 | 未向量化 | 使用NumPy批量计算 |