(以下内容全部来自上述课程)
目录
- 栈
-
- [1. 括号匹配问题](#1. 括号匹配问题)
-
- [1.1 概述](#1.1 概述)
- [1.2 算法演示](#1.2 算法演示)
- [1.3 算法实现](#1.3 算法实现)
- [1.4 小结](#1.4 小结)
- [2. 表达式求值问题](#2. 表达式求值问题)
-
- [2.1 引言](#2.1 引言)
- [2.2 简述](#2.2 简述)
- [2.3 中转后(手算)](#2.3 中转后(手算))
- [2.4 后缀表达式的计算](#2.4 后缀表达式的计算)
-
- [2.4.1 手算](#2.4.1 手算)
- [2.4.2 机算](#2.4.2 机算)
- [2.5 中转前(手算)](#2.5 中转前(手算))
- [2.6 前缀表达式的计算](#2.6 前缀表达式的计算)
- [2.7 小结](#2.7 小结)
- [3. 表达式求值问题(第二季)](#3. 表达式求值问题(第二季))
-
- [3.1 中转后(手算)](#3.1 中转后(手算))
- [3.2 中转后(机算)](#3.2 中转后(机算))
- [3.3 小结](#3.3 小结)
- [4. 栈在递归中的应用](#4. 栈在递归中的应用)
-
- [4.1 函数调用背后的过程](#4.1 函数调用背后的过程)
- [4.2 递归](#4.2 递归)
-
- [4.2.1 阶乘](#4.2.1 阶乘)
- [4.2.2 斐波那契数列](#4.2.2 斐波那契数列)
- [4.3 小结](#4.3 小结)
- 队列
-
- [1. 树的层次遍历](#1. 树的层次遍历)
- [2. 图的广度优先遍历](#2. 图的广度优先遍历)
- [3. 在操作系统中的应用](#3. 在操作系统中的应用)
- 矩阵的压缩存储
-
- [1. 数组的存储结构](#1. 数组的存储结构)
-
- [1.1 一维数组的存储结构](#1.1 一维数组的存储结构)
- [1.2 二维数组的存储结构](#1.2 二维数组的存储结构)
- [2. 矩阵的存储结构](#2. 矩阵的存储结构)
-
- [2.1 普通矩阵](#2.1 普通矩阵)
- [2.2 对称矩阵](#2.2 对称矩阵)
- [2.3 三角矩阵](#2.3 三角矩阵)
- [2.4 带状矩阵](#2.4 带状矩阵)
- [2.5 稀疏矩阵](#2.5 稀疏矩阵)
- [2.6 小结](#2.6 小结)
栈
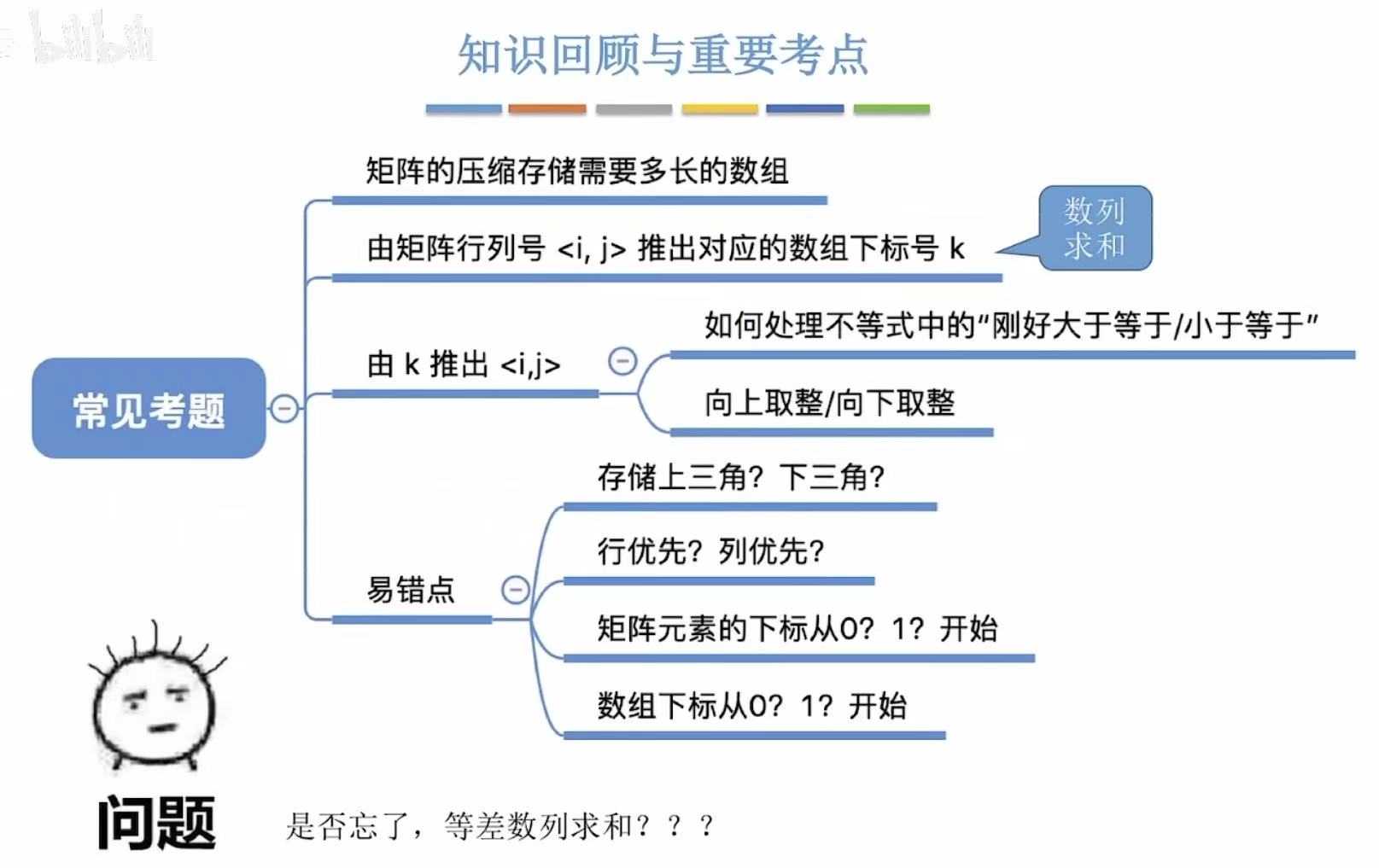
1. 括号匹配问题
1.1 概述
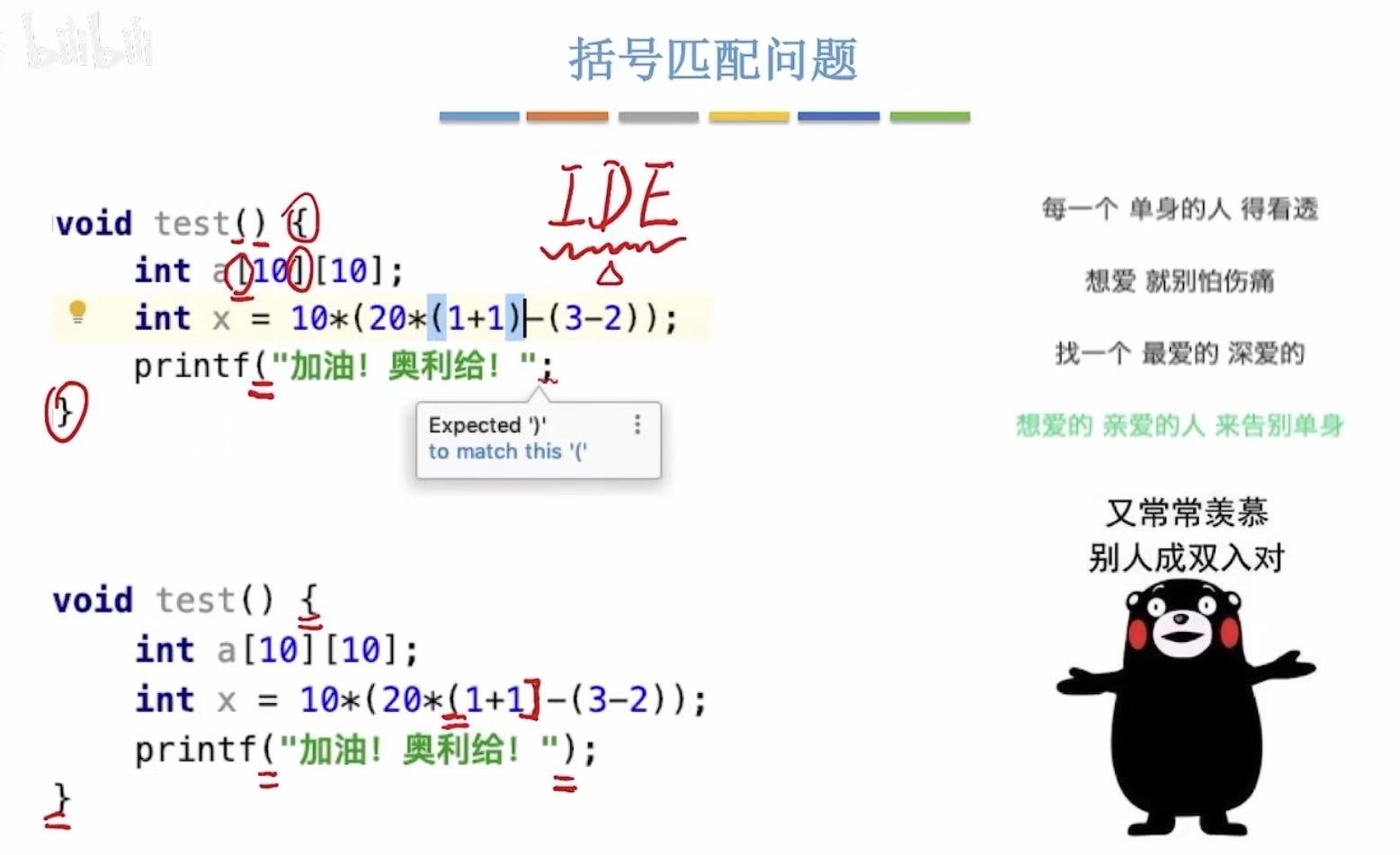
当我们打代码的时候,如果我们一不小心落下一个右括号,编译器就会报错提示我们。
接下来我们就要具体了解,为什么编译器可以看出来我们少了一个括号。
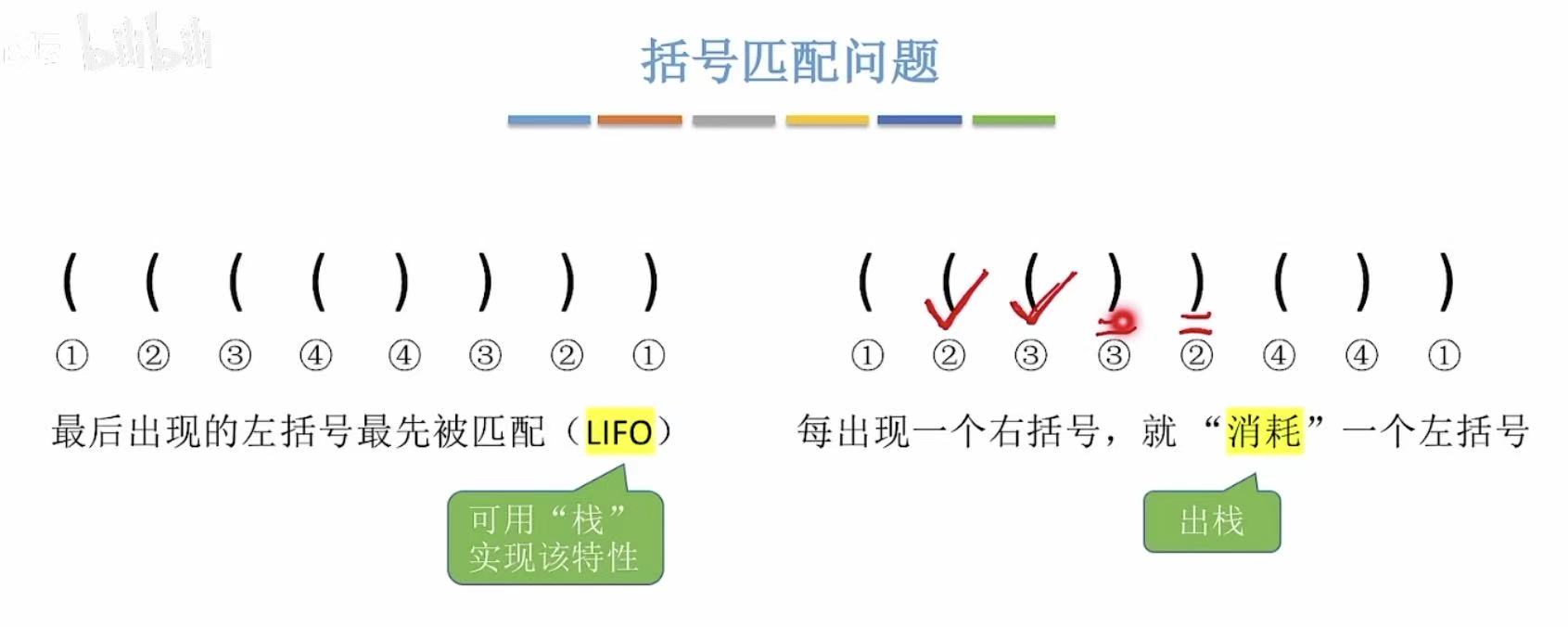
最后出现的左括号最先被匹配走(最里层被外层包起来了)
这就符合后进先出的性质,也就是栈的性质,就可以用栈来帮我们解决这个问题。
1.2 算法演示
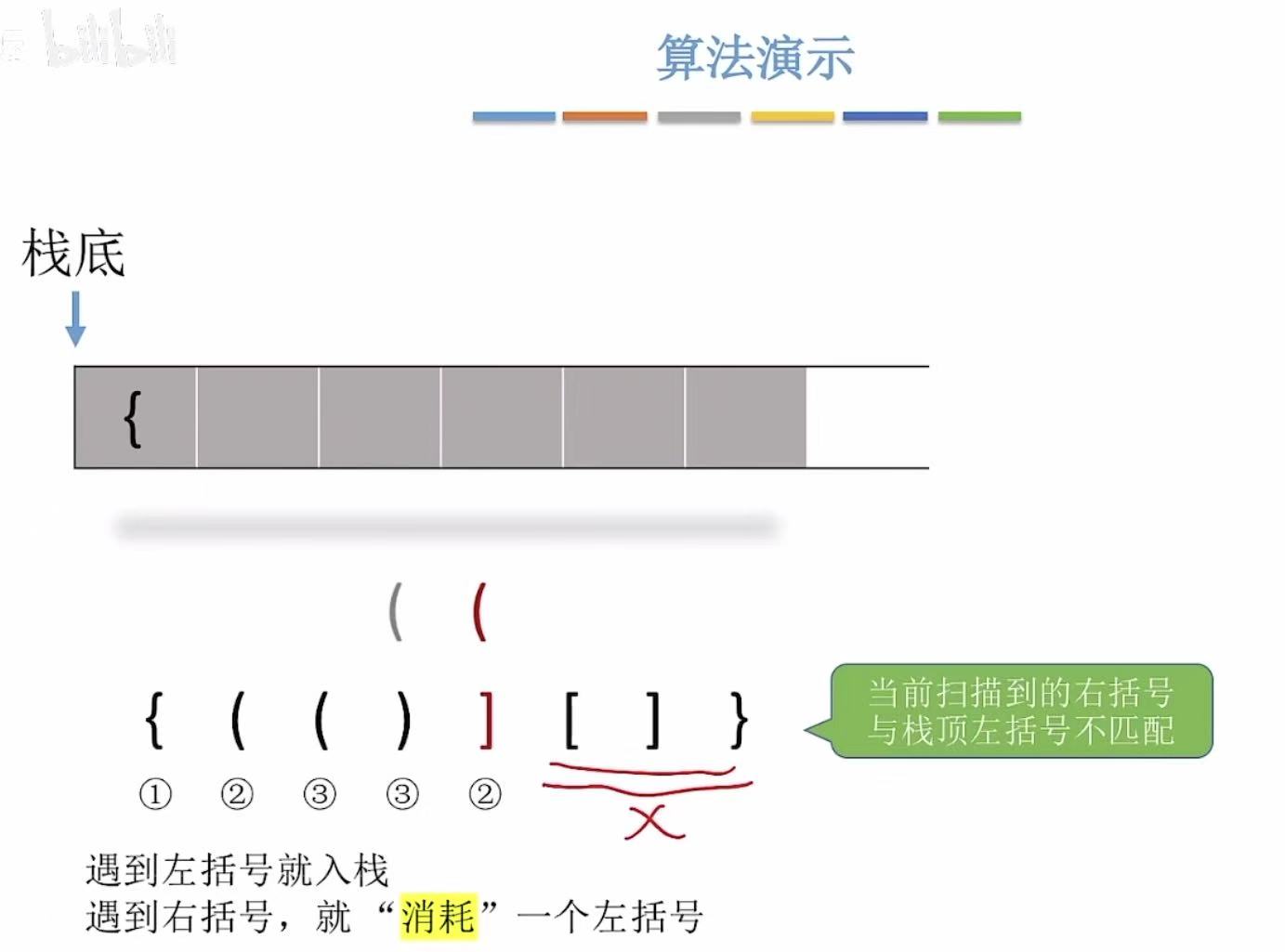
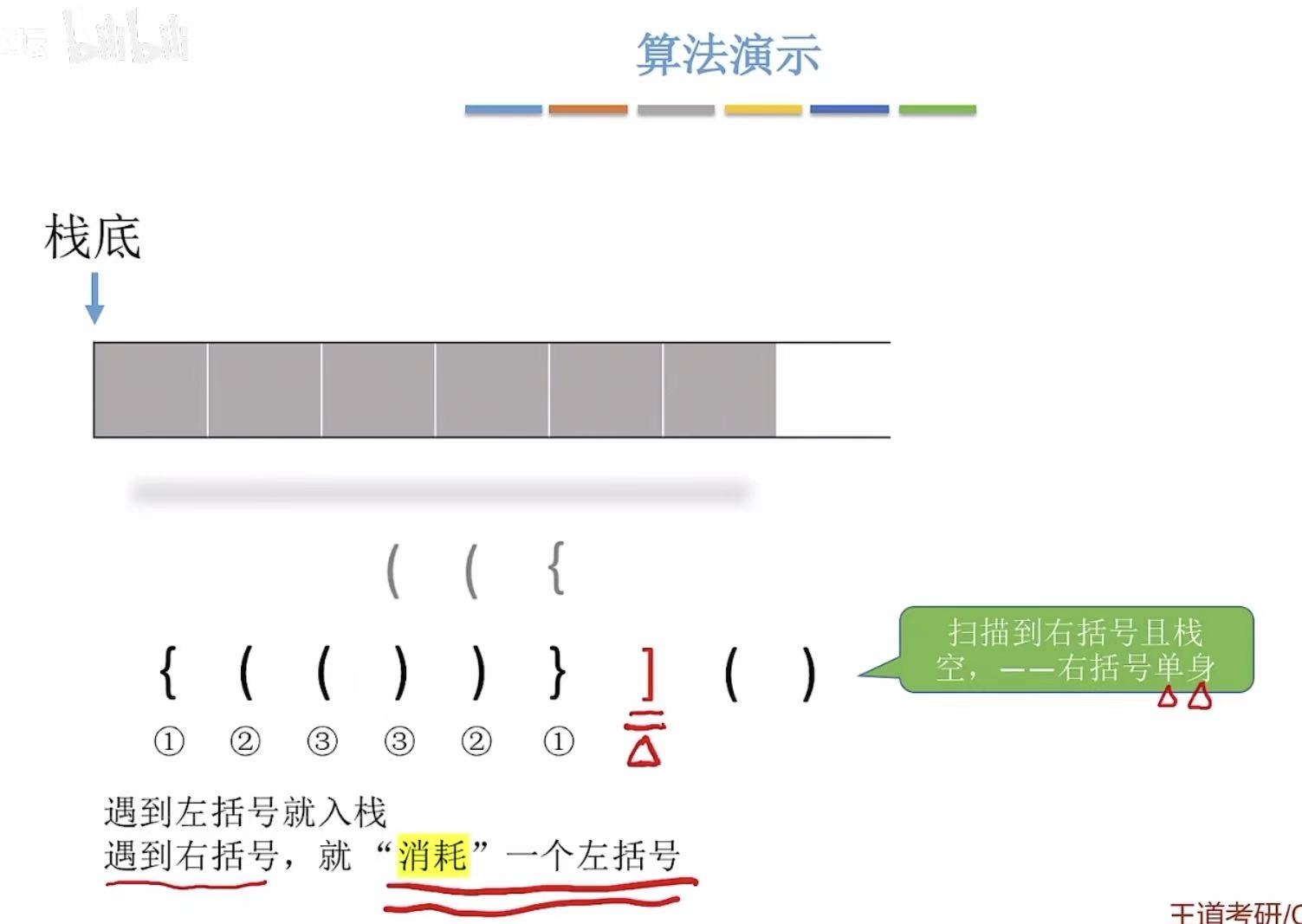
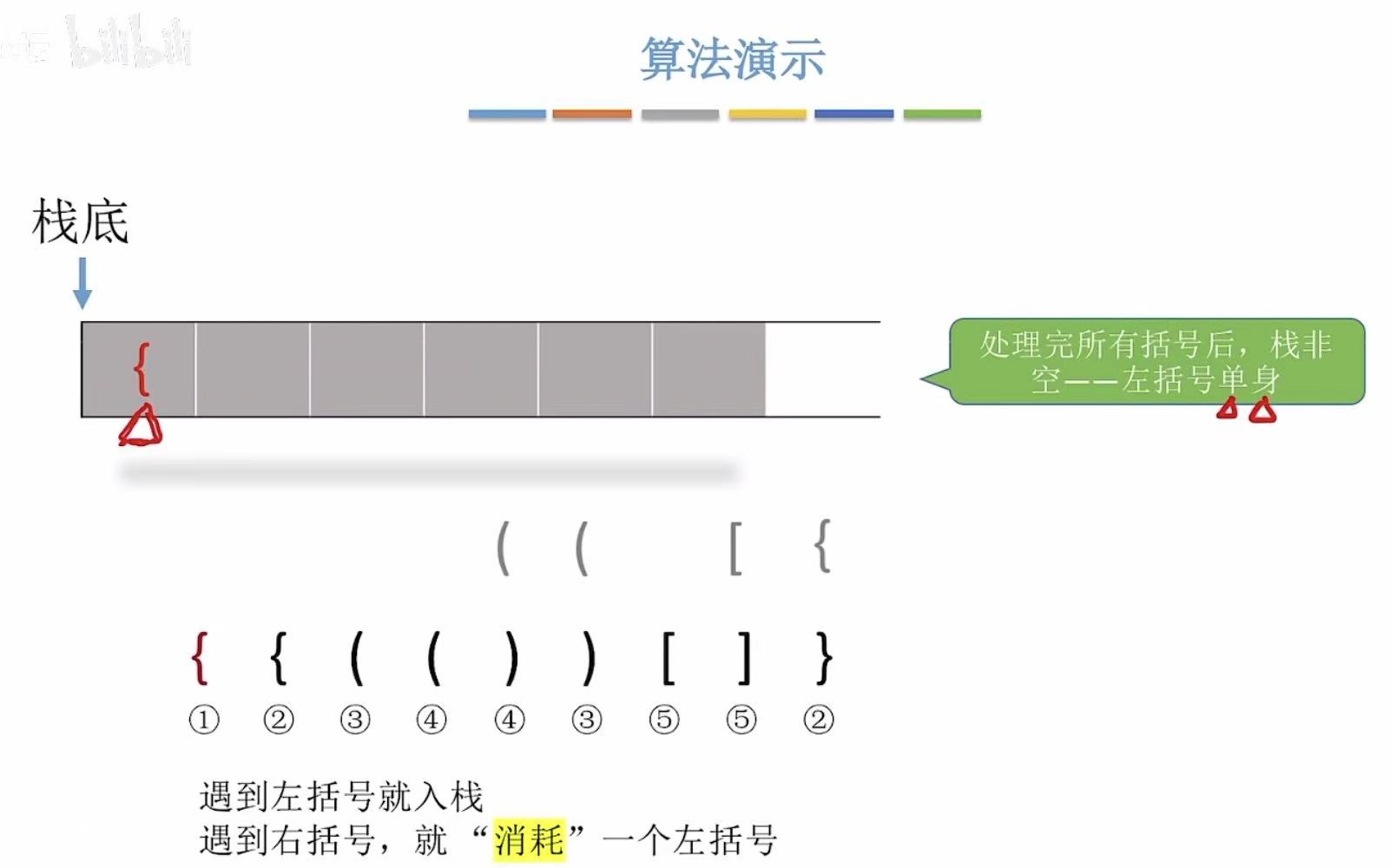
遵循规则:
- 左括号-->入栈
- 右括号-->左括号出栈进行匹配
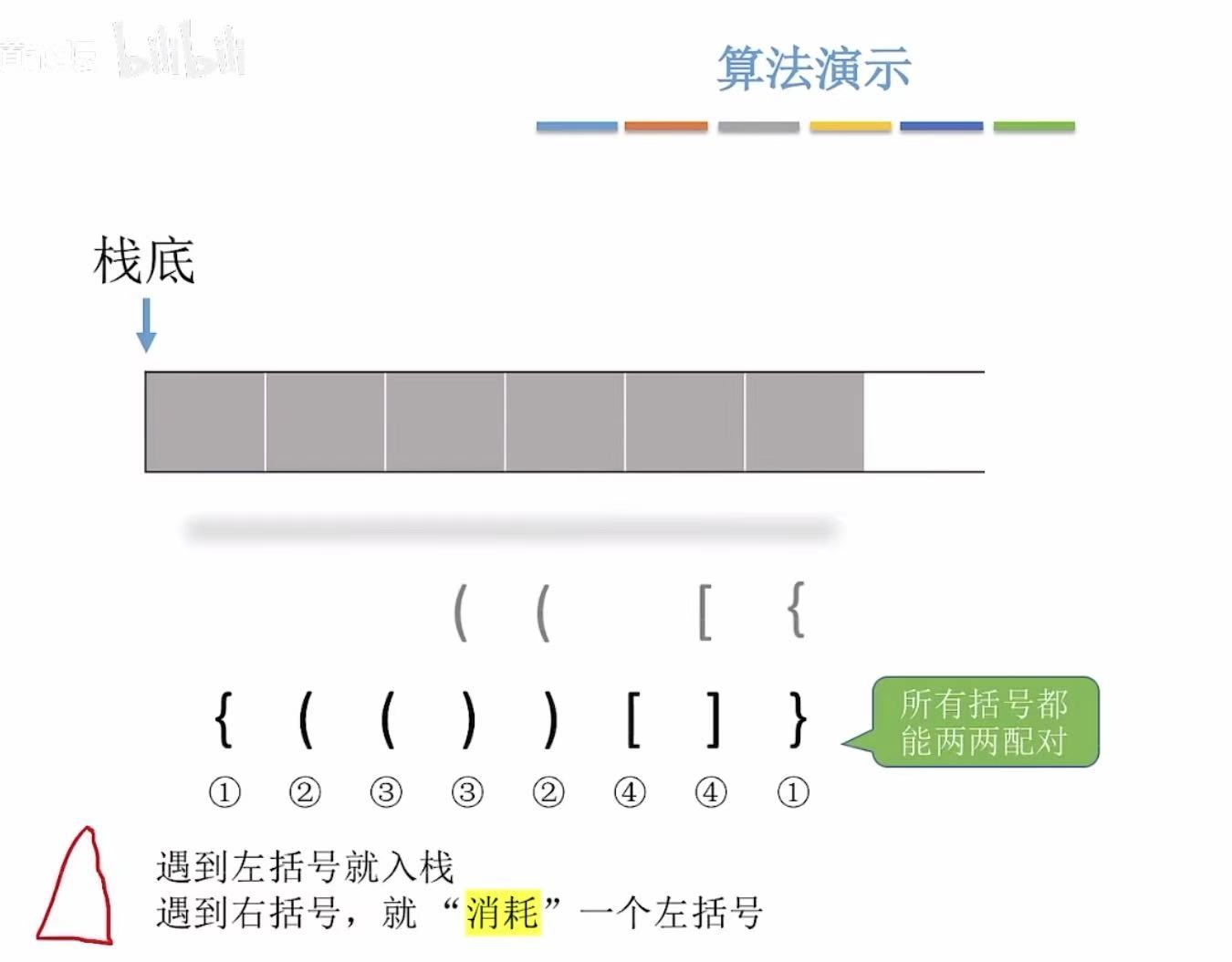
- 左右括号不匹配
- 右括号单身-->缺少一个左括号
- 左括号单身-->缺少一个右括号
将上述的逻辑进行整合,就可以形成如下的流程图:
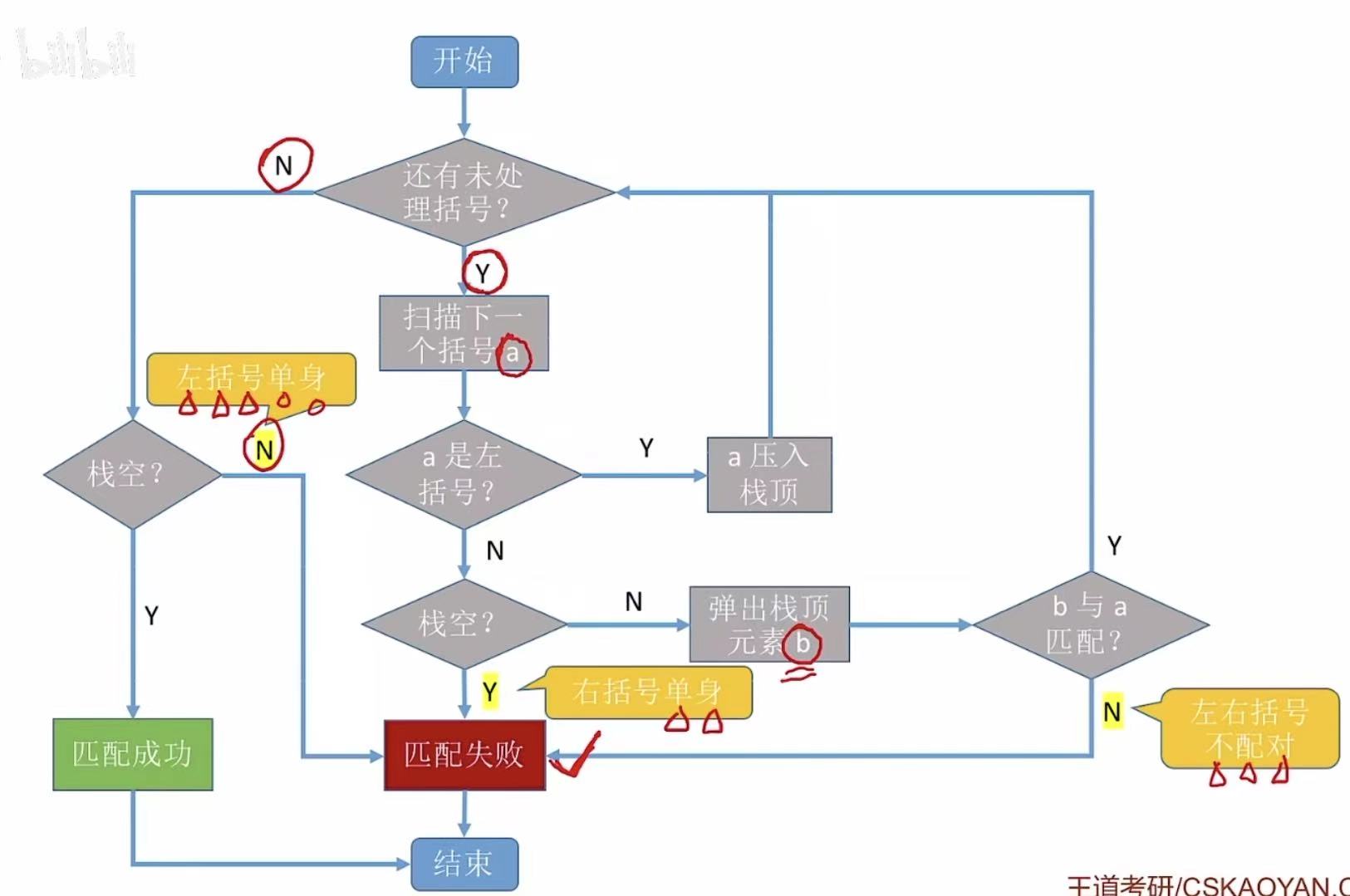
1.3 算法实现

1.4 小结

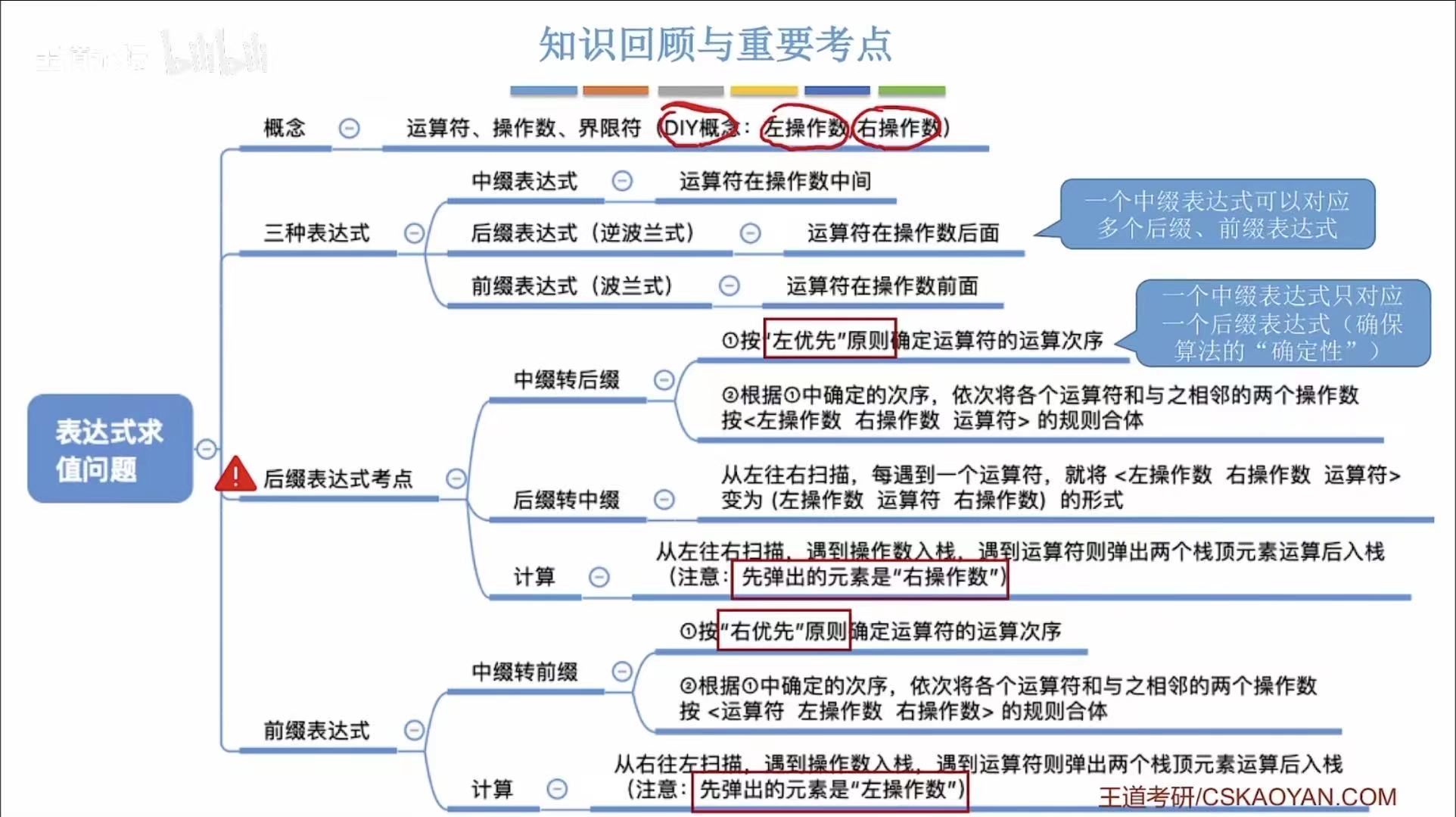
2. 表达式求值问题
2.1 引言
- 操作数:阿拉伯数字,1,2,3...
- 运算符:+、-、*、/...
- 界限符 :就是括号

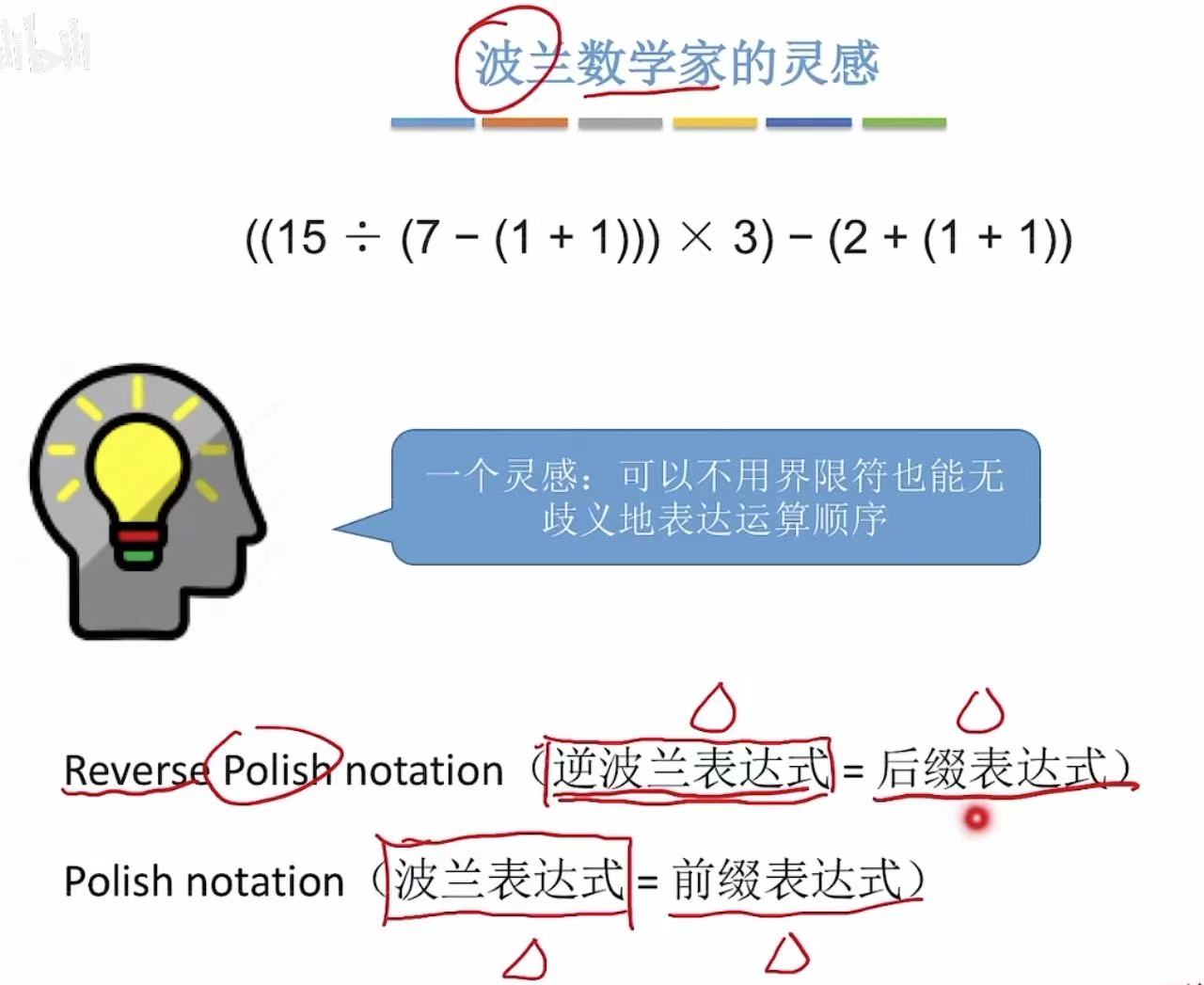
正常就是上面的表达式,但是有一个数学家就突发奇想:可不可以不用括号表示这些算式呢
所以就出现了前缀 表达式和后缀 表达式
因为是波兰数学家想出来的,所以还叫波兰 表达式和逆波兰 表达式
2.2 简述
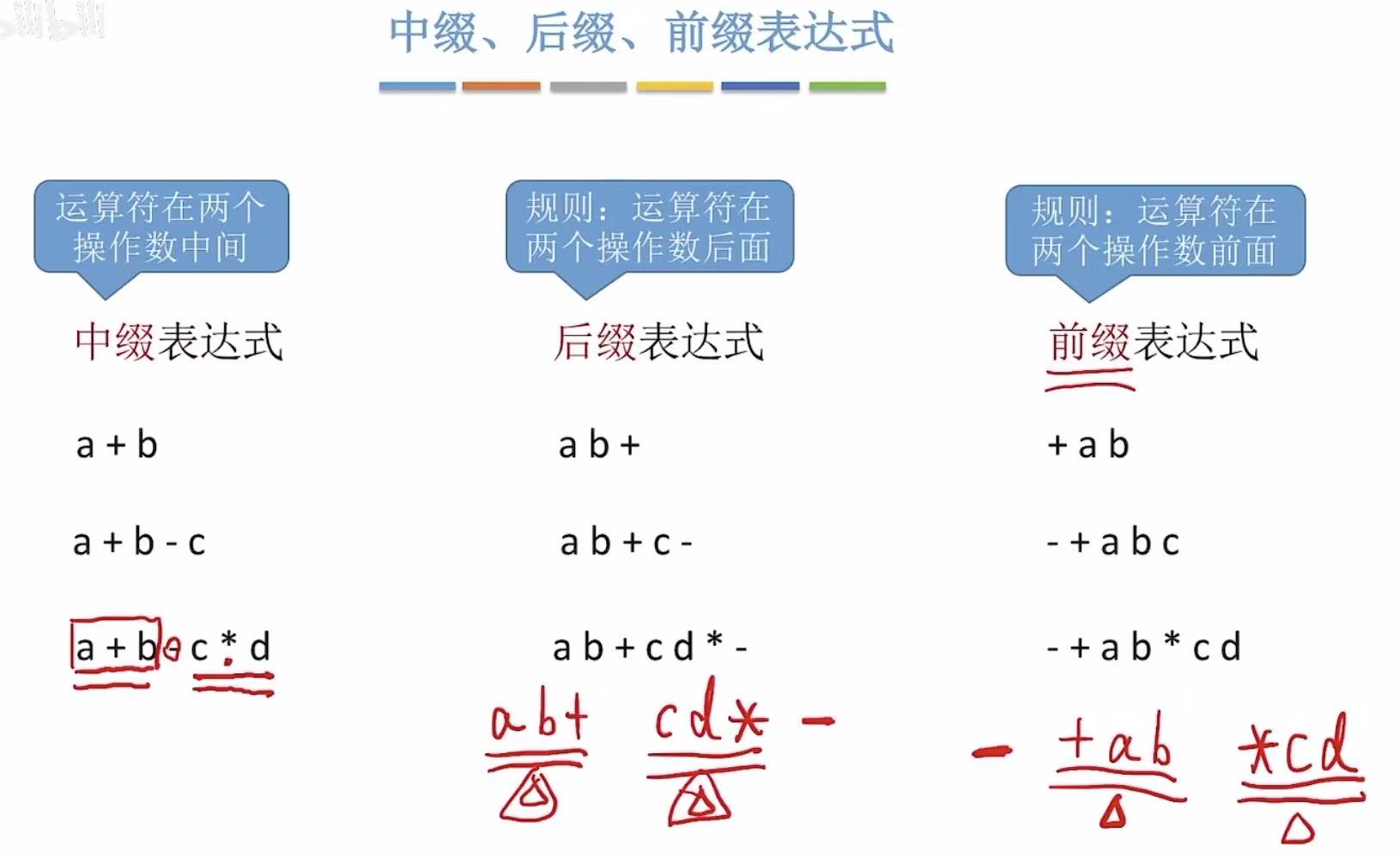
- 中缀:运算符在两个操作数中间
- 后缀:运算符在两个操作数后面
- 前缀 :运算符在两个操作数前面
2.3 中转后(手算)
观察点:第一排表达式的运算符顺序与第二排表达式的运算符顺序不一样

- 运算顺序不唯一,因此对应的后缀表达式也不唯一
- 那么我们如果想让两排表达式的运算符顺序一样该怎么做呢?
- 这就出现了我们需要学习的左优先原则 (见左侧图片效果)!
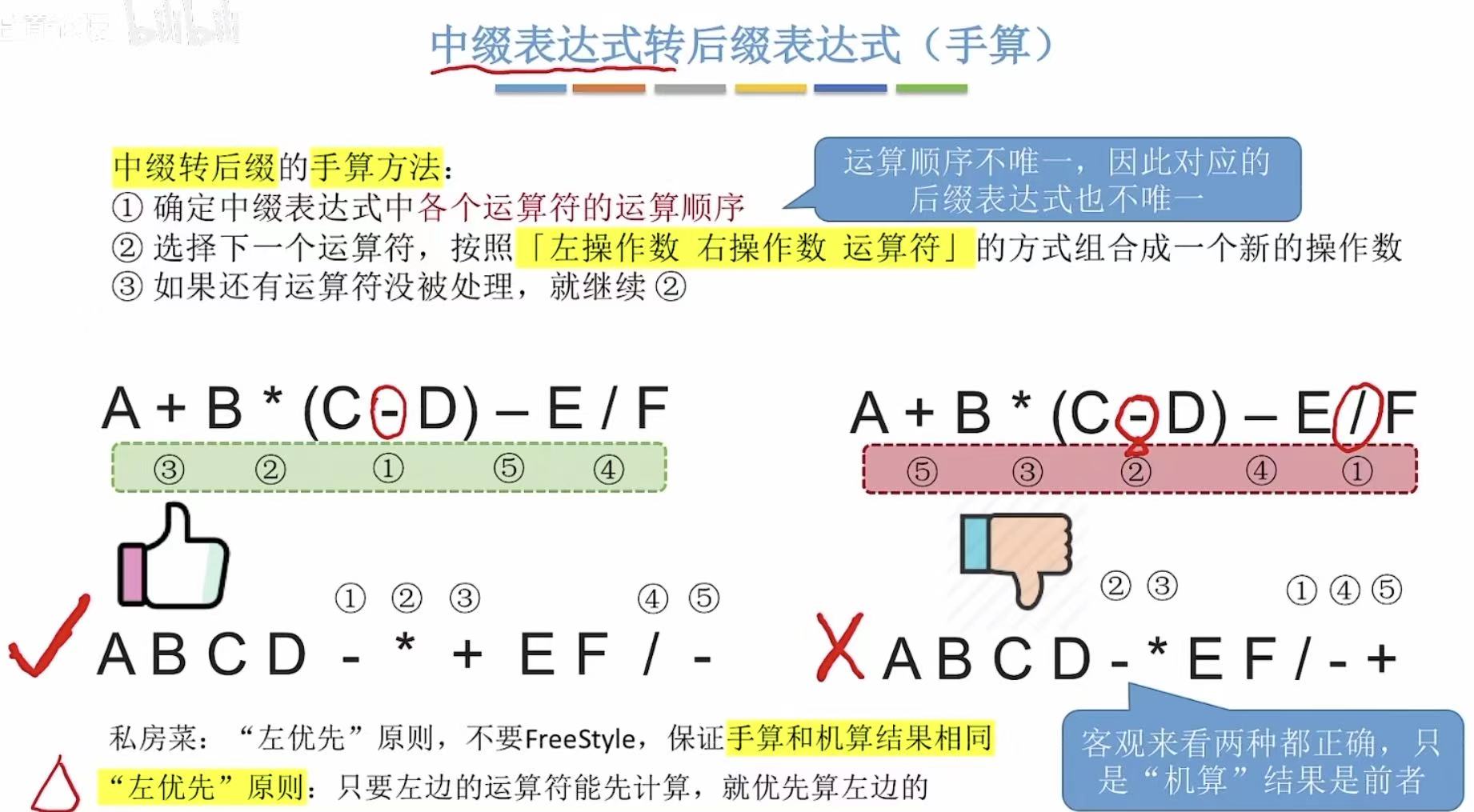
使用左优先原则,就可以保证运算顺序唯一。
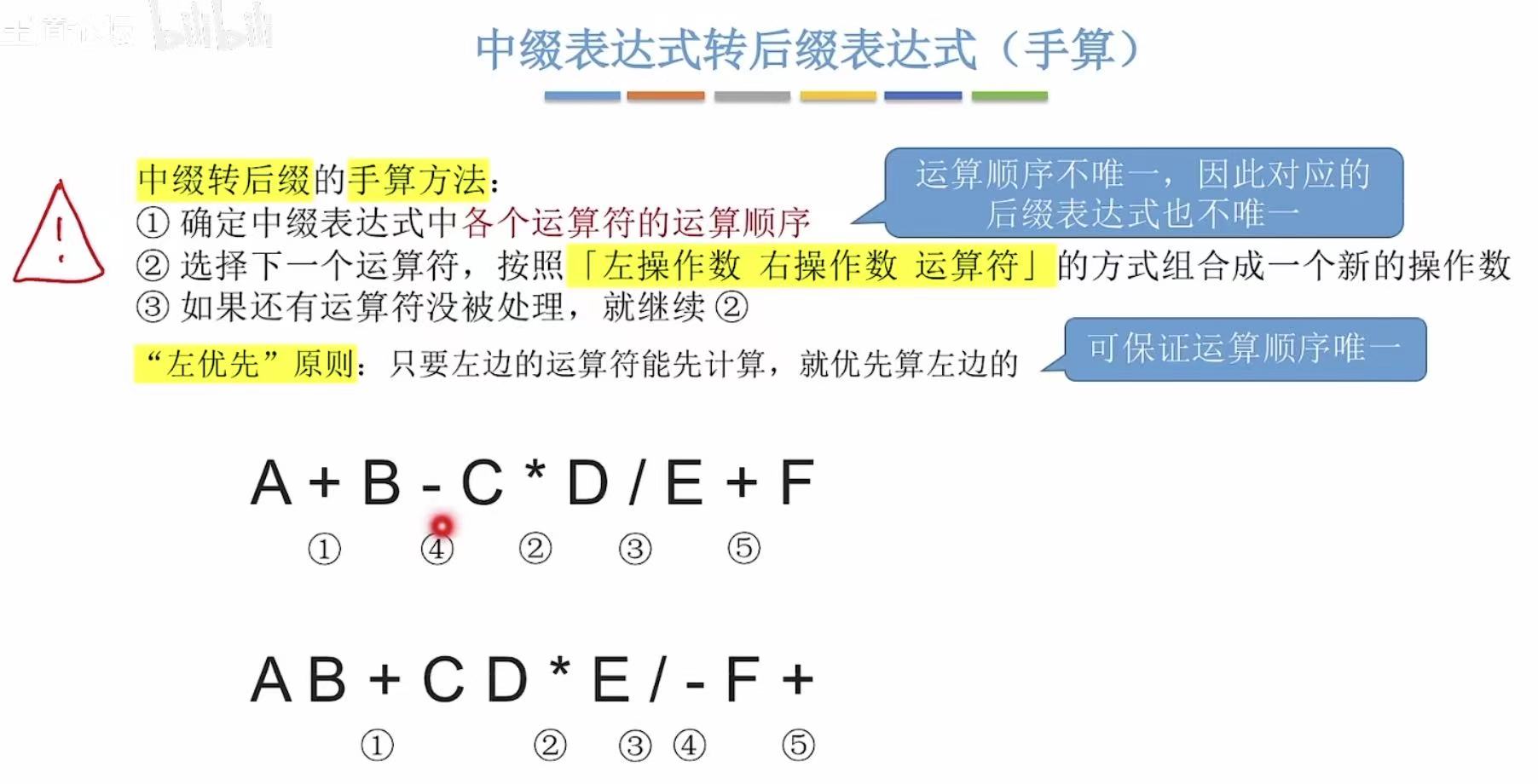
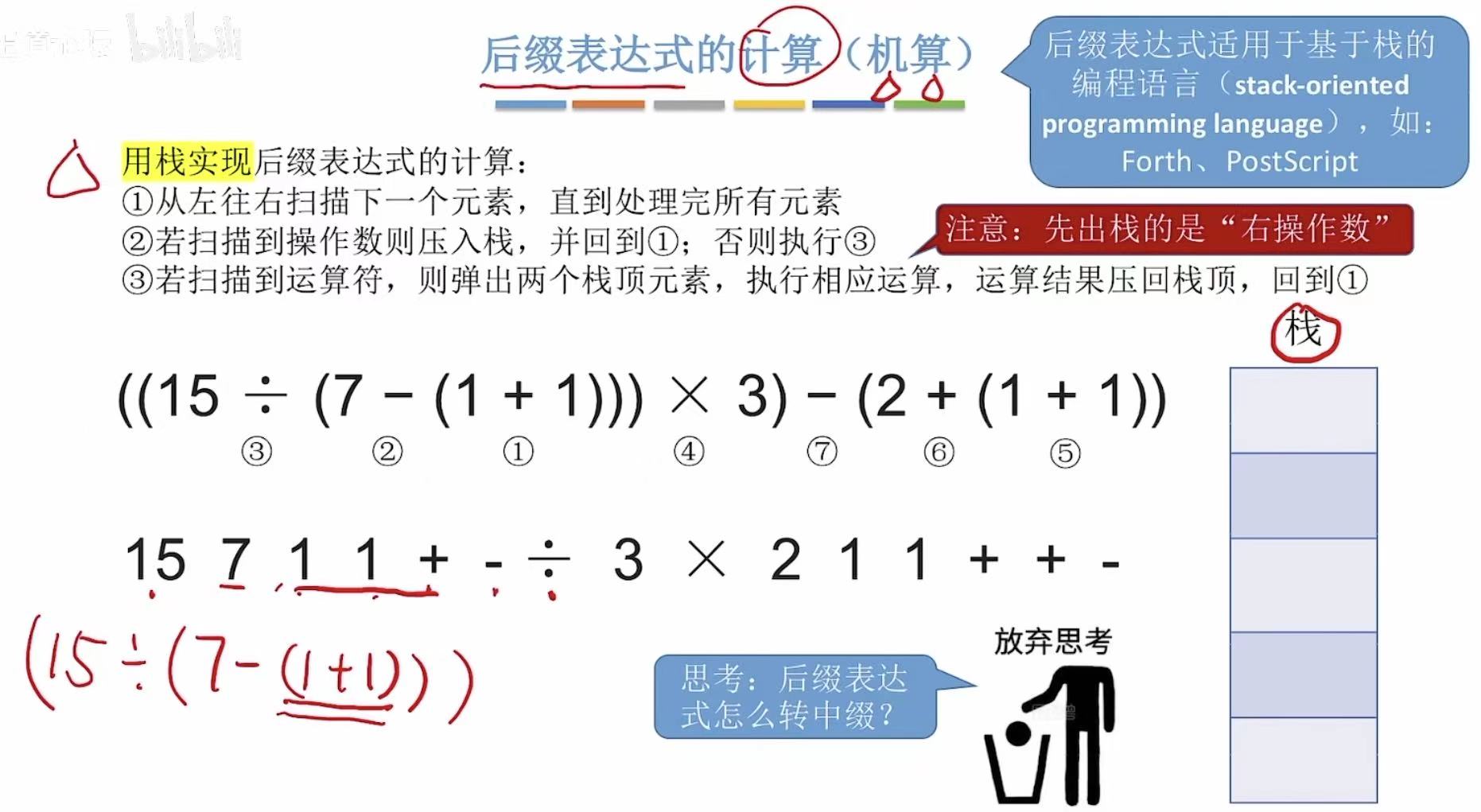
2.4 后缀表达式的计算
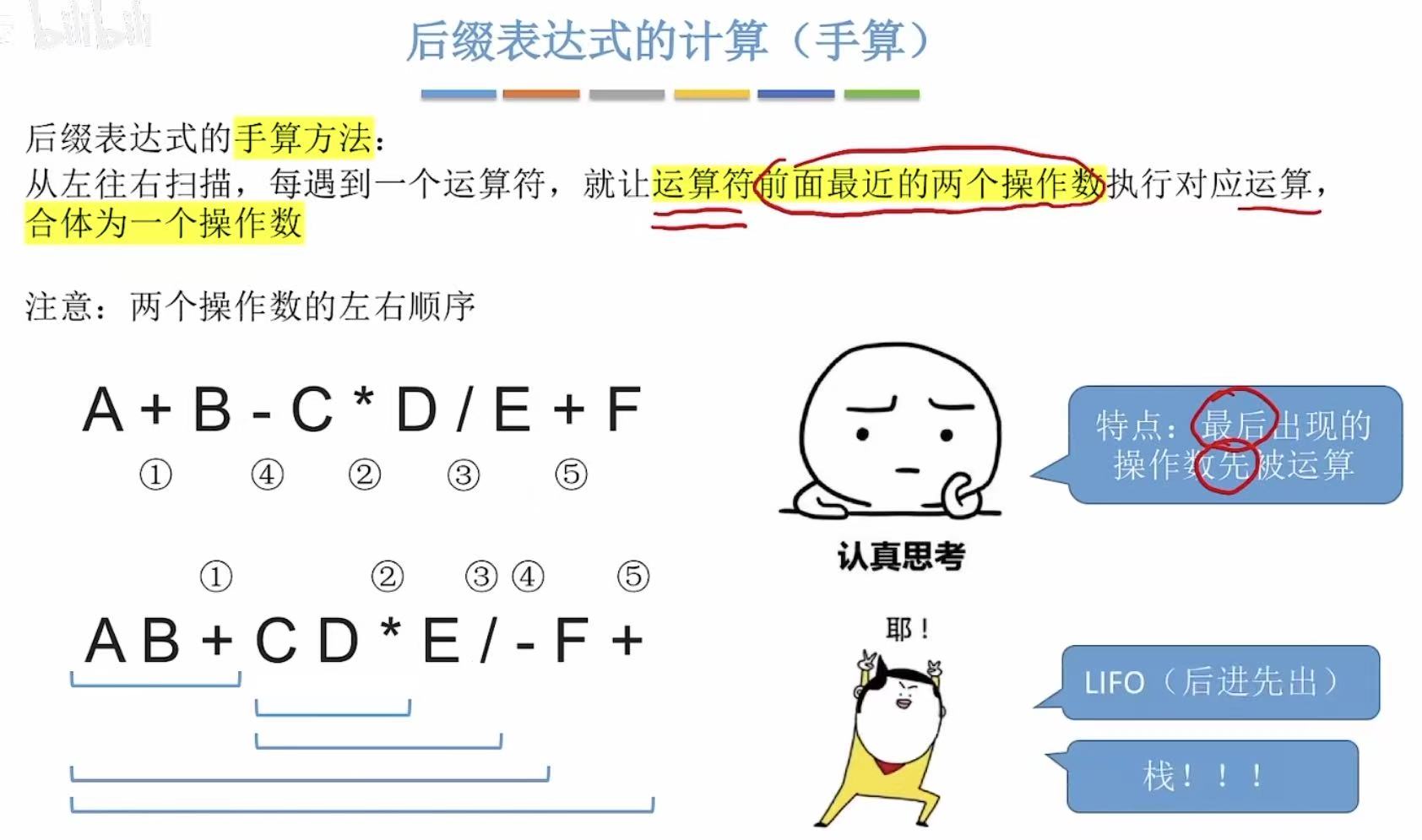
2.4.1 手算
操作数操作数运算符 = 一个式子 = 下一次计算的操作数
如上,一直套娃就可以得到最终结果。

最后出现的操作数才能和最先出现的操作数经过运算符的匹配进行计算,所以也属于一种后进先出,可以用栈来实现。
2.4.2 机算
java
表达式: A B + C D * E / - F +
步骤 栈内容(从底到顶)
1. A [A]
2. B [A, B]
3. + [A+B]
4. C [A+B, C]
5. D [A+B, C, D]
6. * [A+B, C*D]
7. E [A+B, C*D, E]
8. / [A+B, (C*D)/E]
9. - [(A+B) - ((C*D)/E)]
10. F [(A+B)-((C*D)/E), F]
11. + [((A+B)-((C*D)/E)) + F]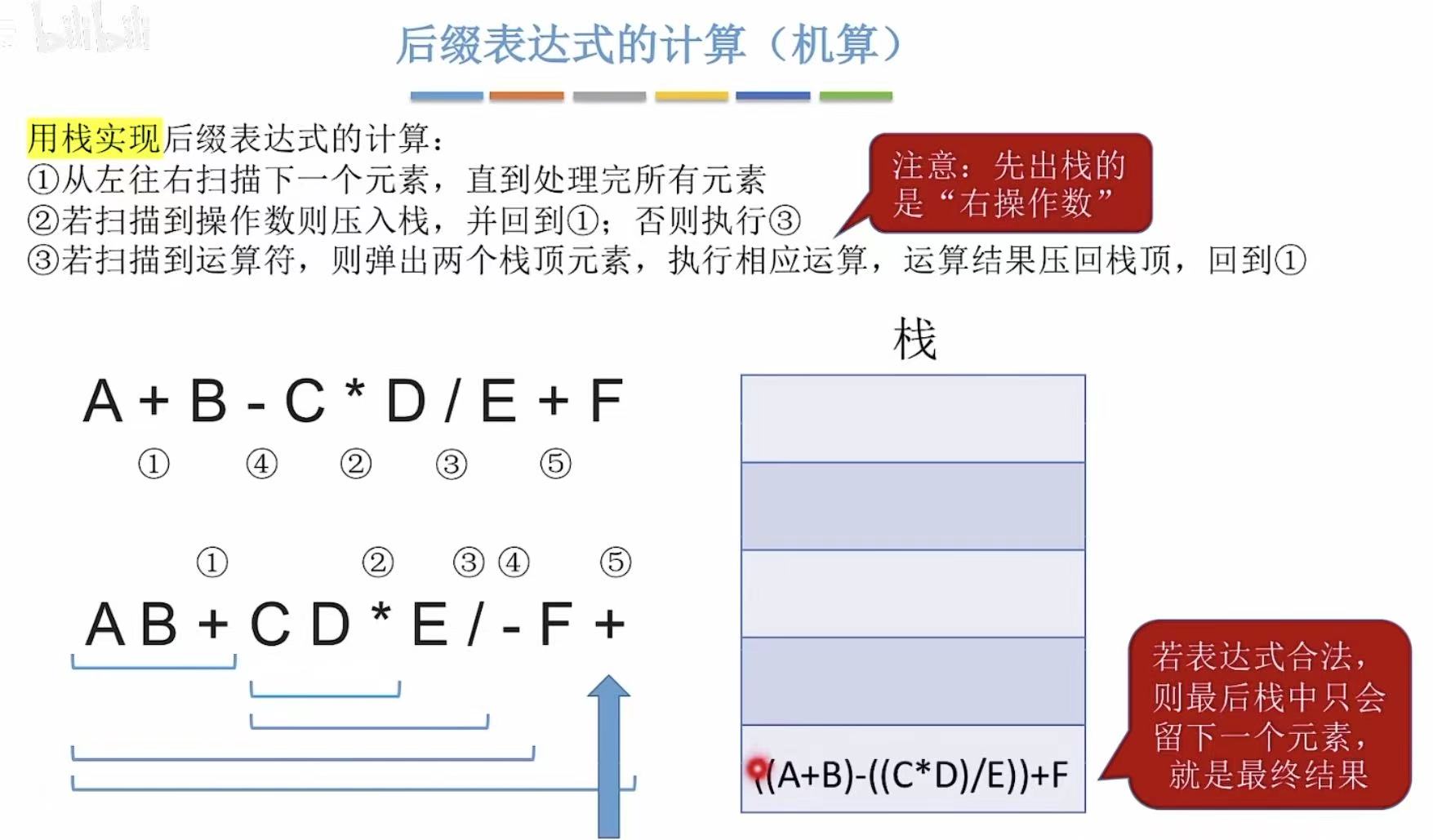
换成具体的例子:
2.5 中转前(手算)
之前提到后缀表达式是左优先原则
转为前缀表达式就完全反过来了,就是右优先原则。


2.6 前缀表达式的计算
和后缀表达式的计算除了反过来,剩余完全相同。
| 步骤 | 元素 | 栈(从底到顶) | 说明 |
|---|---|---|---|
| 1 | 1 | [1] | 入栈 |
| 2 | 1 | [1,1] | 入栈 |
| 3 | + | [2] | 1+1=2 |
| 4 | 2 | [2,2] | 入栈 |
| 5 | + | [4] | 2+2=4 |
| 6 | 3 | [4,3] | 入栈 |
| 7 | 1 | [4,3,1] | 入栈 |
| 8 | 1 | [4,3,1,1] | 入栈 |
| 9 | + | [4,3,2] | 1+1=2 |
| 10 | 7 | [4,3,2,7] | 入栈 |
| 11 | - | [4,3,5] | 7-2=5 |
| 12 | 15 | [4,3,5,15] | 入栈 |
| 13 | ÷ | [4,3,3] | 15÷5=3 |
| 14 | × | [4,9] | 3×3=9 |
| 15 | - | [5] | 9-4=5 |

2.7 小结
3. 表达式求值问题(第二季)
3.1 中转后(手算)

3.2 中转后(机算)
正常没有括号的形式:

加了括号之后的形式:
| 步骤 | 字符 | 栈内容(从底到顶) | 后缀表达式 |
|---|---|---|---|
| 1 | A | [] | A |
| 2 | + | [+] | A |
| 3 | B | [+] | AB |
| 4 | * | [+, *] | AB |
| 5 | ( | [+, *, (] | AB |
| 6 | C | [+, *, (] | ABC |
| 7 | - | [+, *, (, -] | ABC |
| 8 | D | [+, *, (, -] | ABCD |
| 9 | ) | [+, *] | ABCD - * |
| 10 | - | [-] | ABCD - * + |
| 11 | E | [-] | ABCD - * + E |
| 12 | / | [-, /] | ABCD - * + E |
| 13 | F | [-, /] | ABCD - * + E F |
| 14 | (结束) | [-, /] | ABCD - * + E F / - |

换成具体的例子:

3.3 小结

4. 栈在递归中的应用
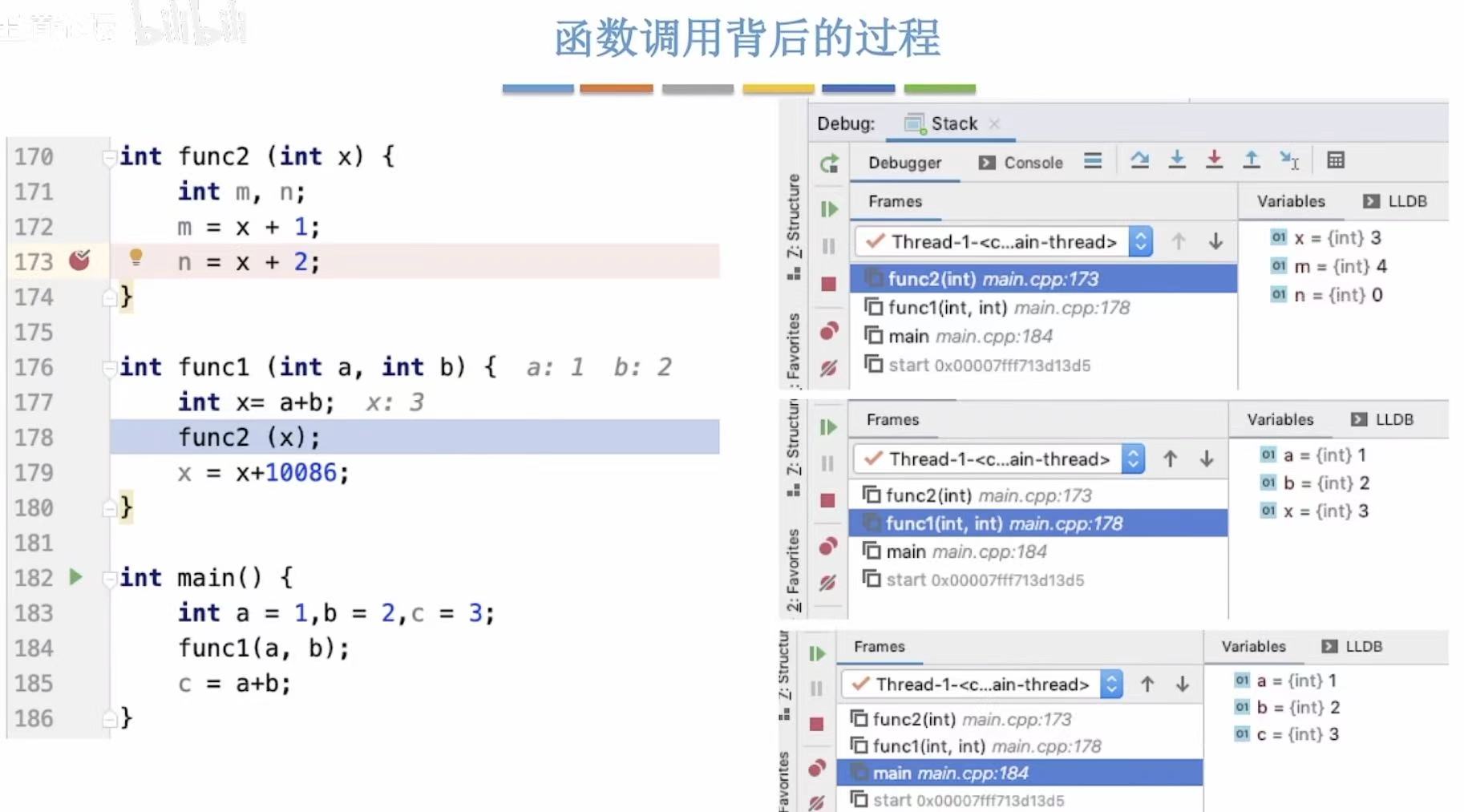
4.1 函数调用背后的过程
A调用B-->B调用C-->C结束-->B继续执行-->B结束-->A继续执行-->A结束
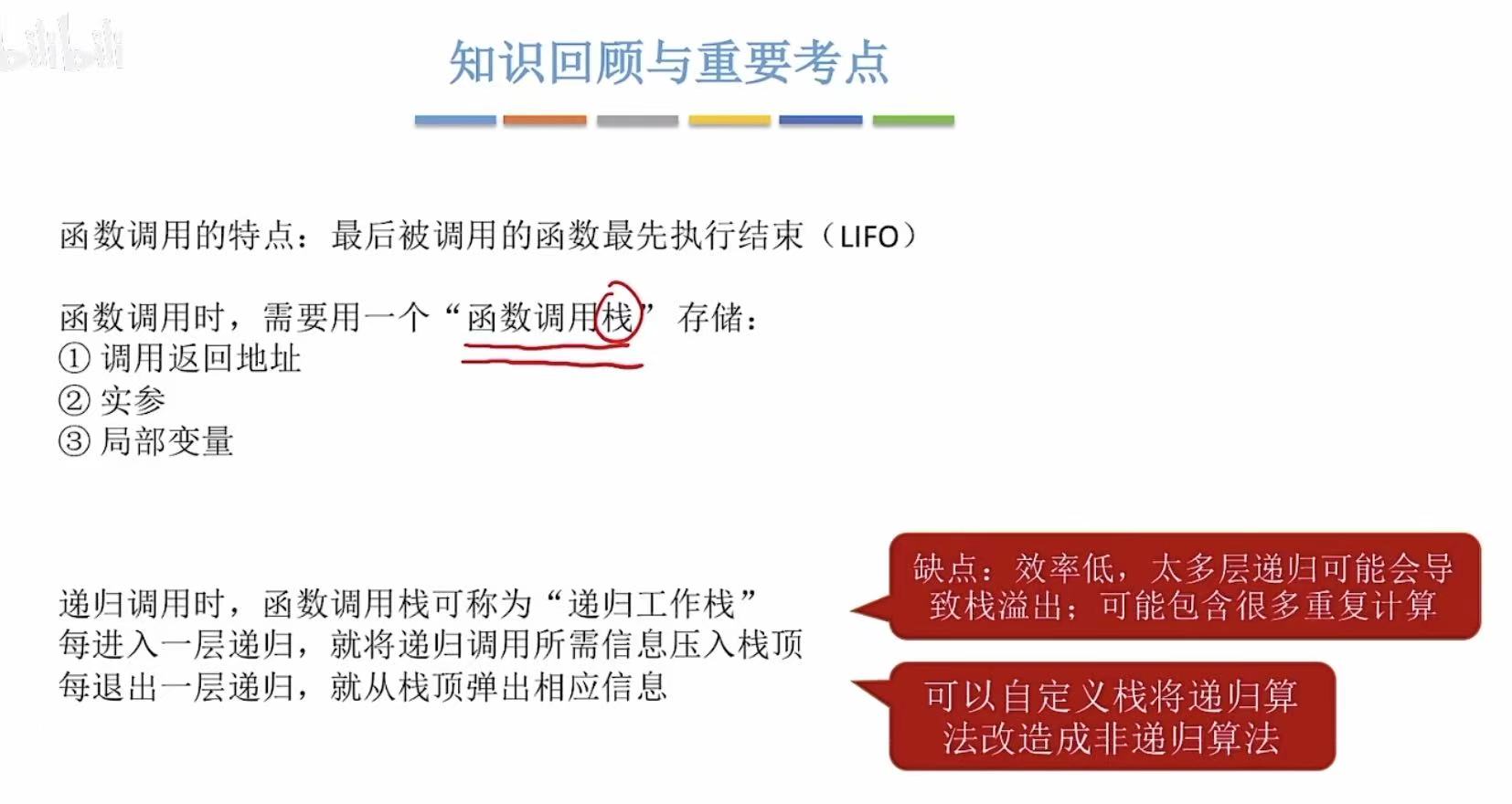
由此可见,最后调用的函数最先结束,符合后进先出的特性,所以可以用栈来实现。
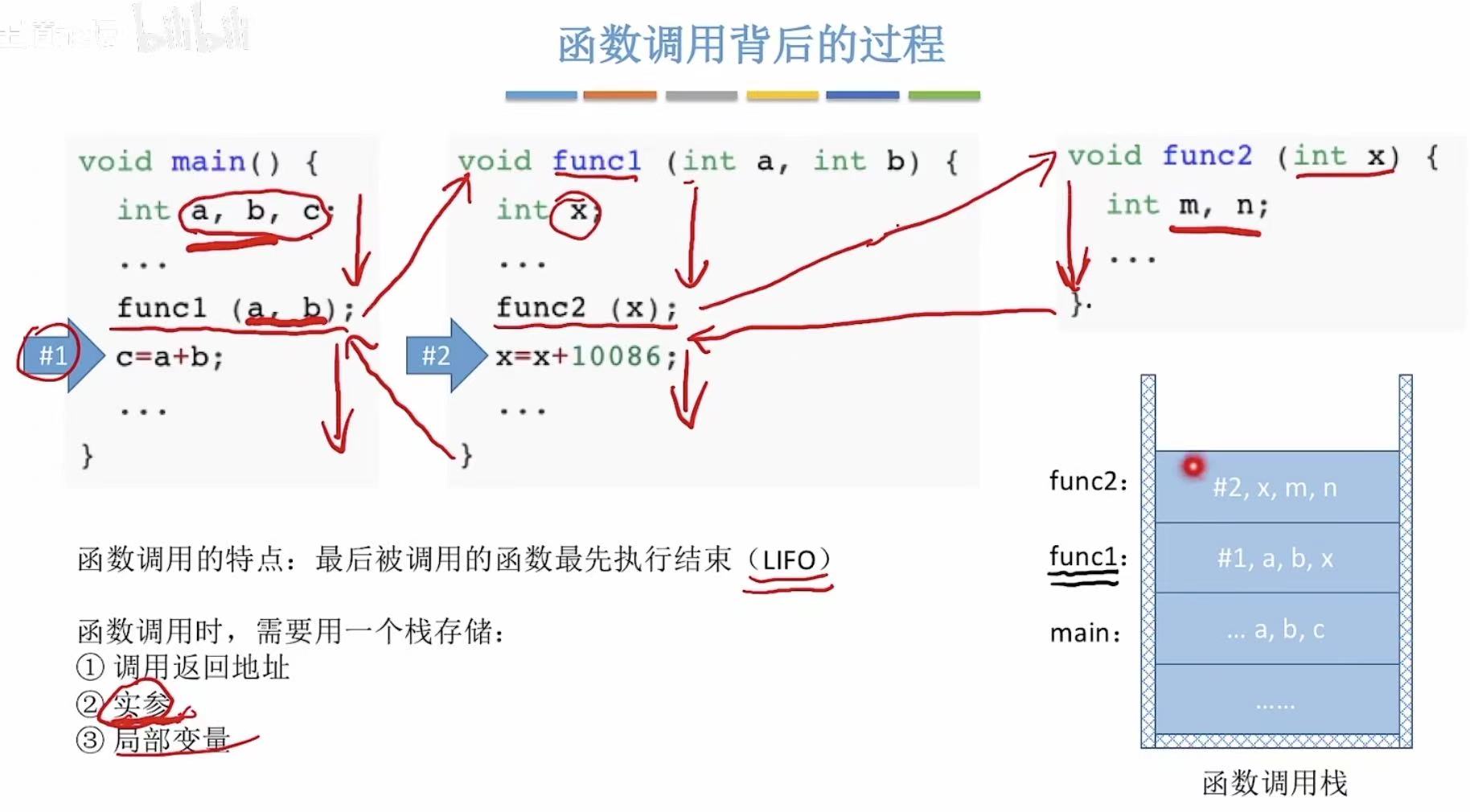
在IDE中,我们可以通过打不同的断点来观察每个阶段,栈中的情况怎么样。
4.2 递归
递归就是自己调用自己。
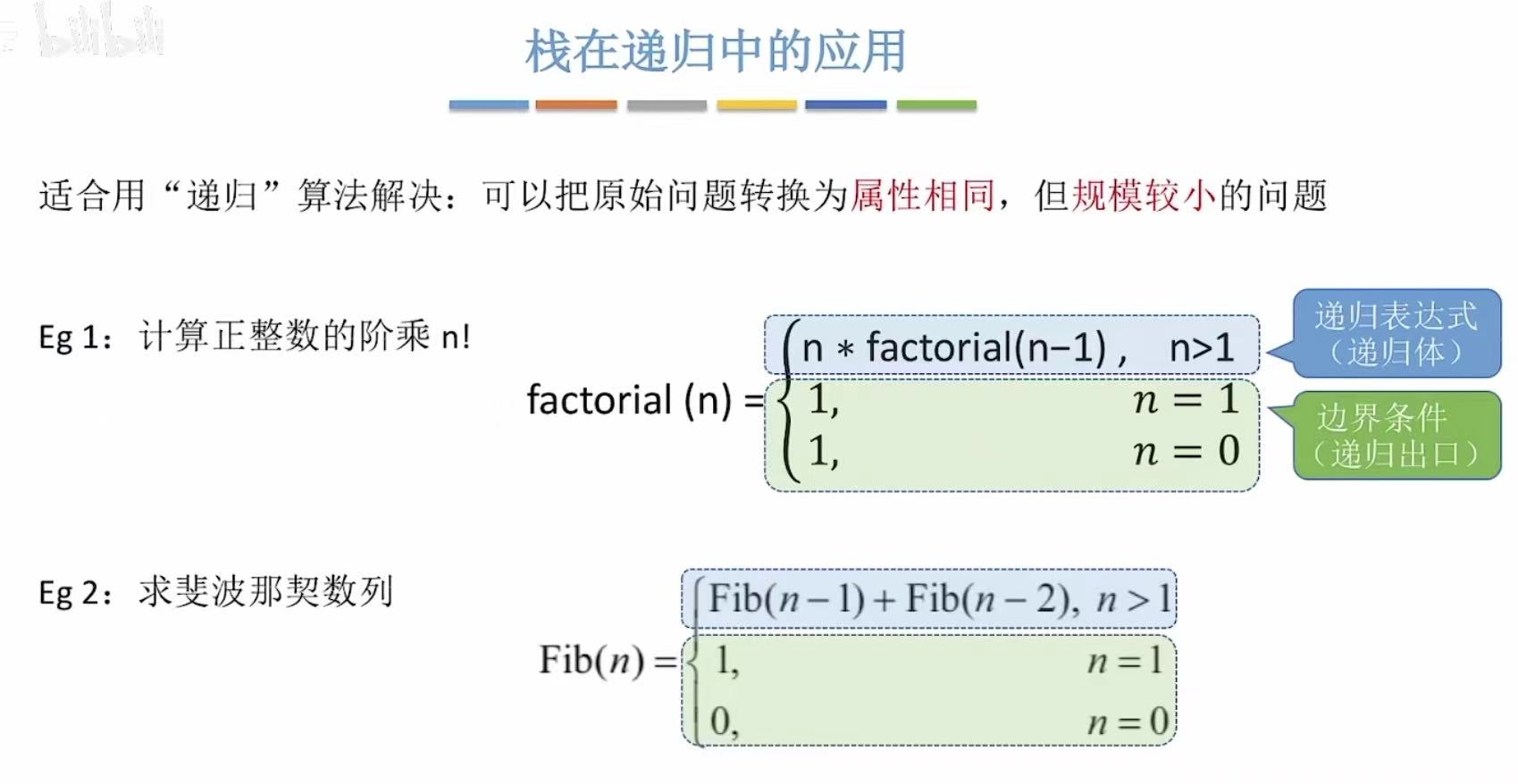
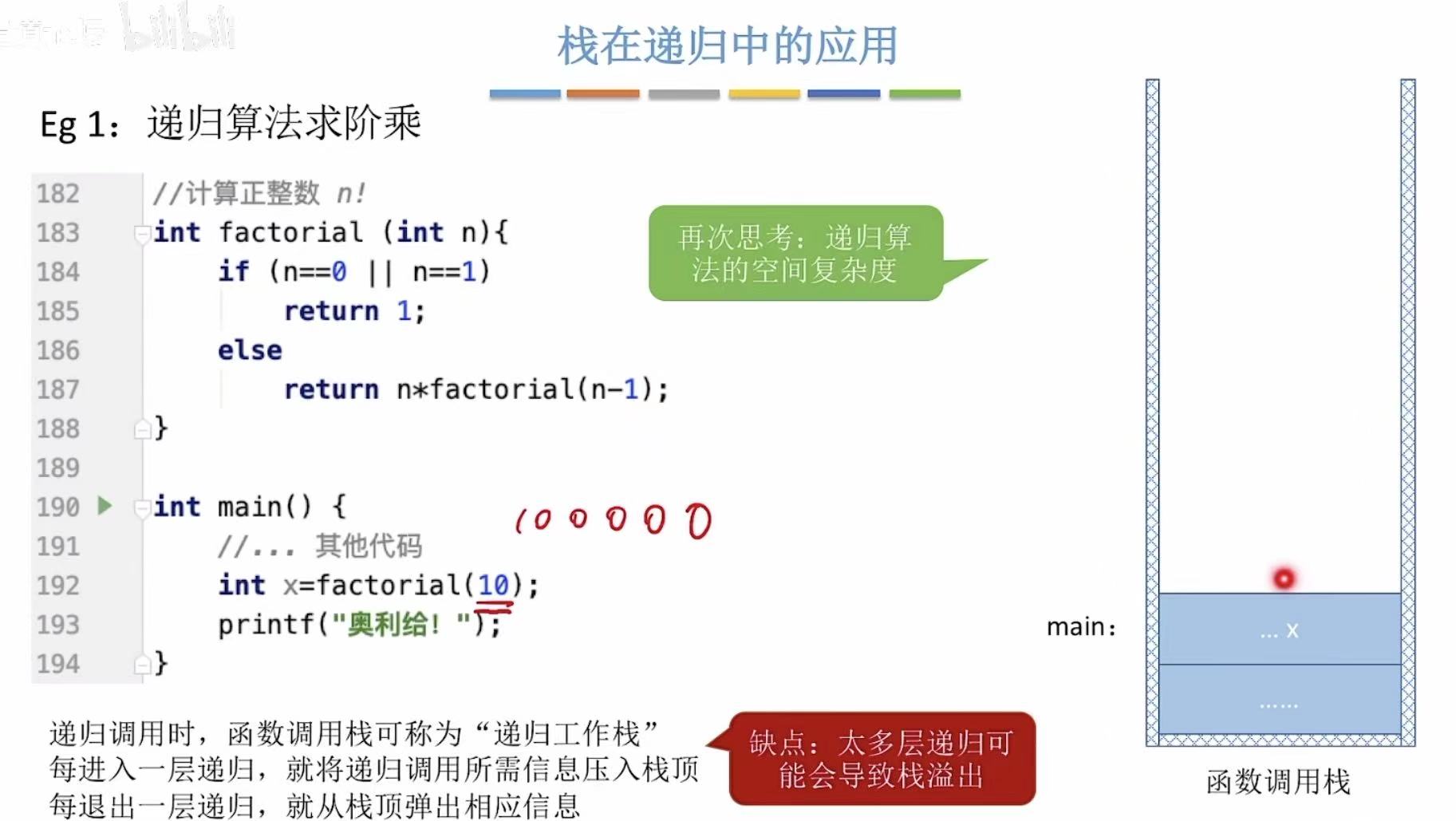
4.2.1 阶乘
栈底-->栈顶:n=10-->n=1

栈顶-->栈底:98 76 54 32 1

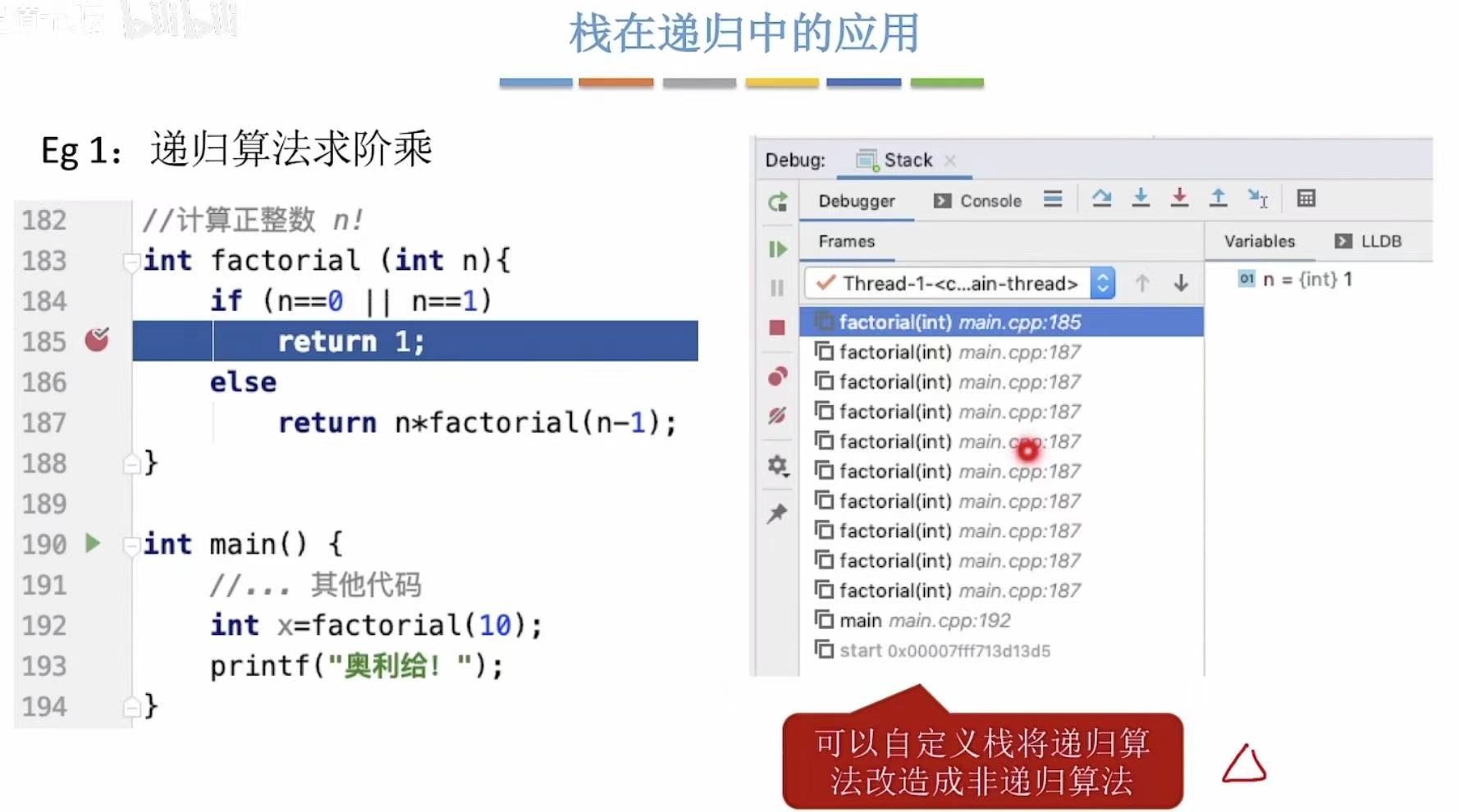
IDE可以查看栈中元素
4.2.2 斐波那契数列
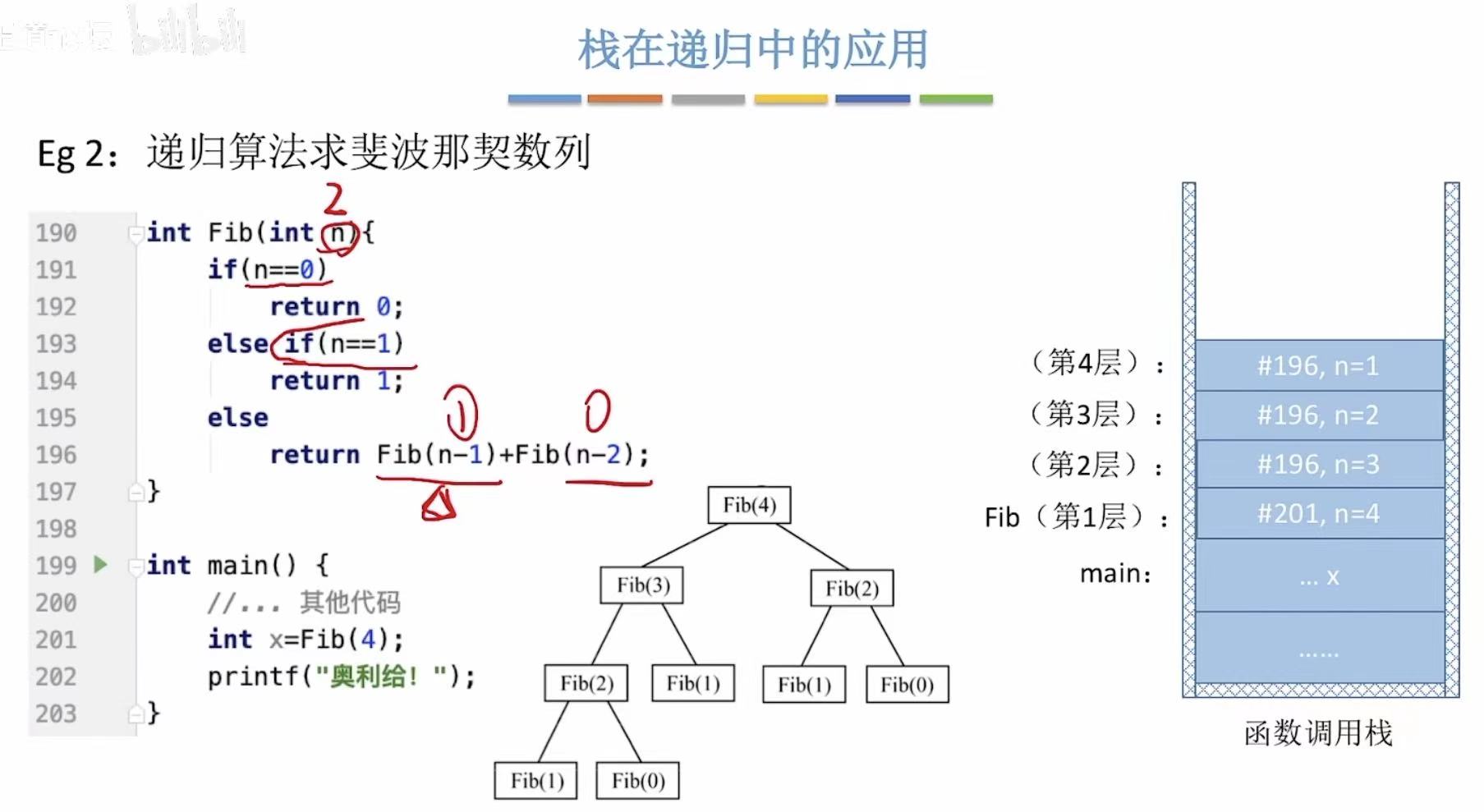
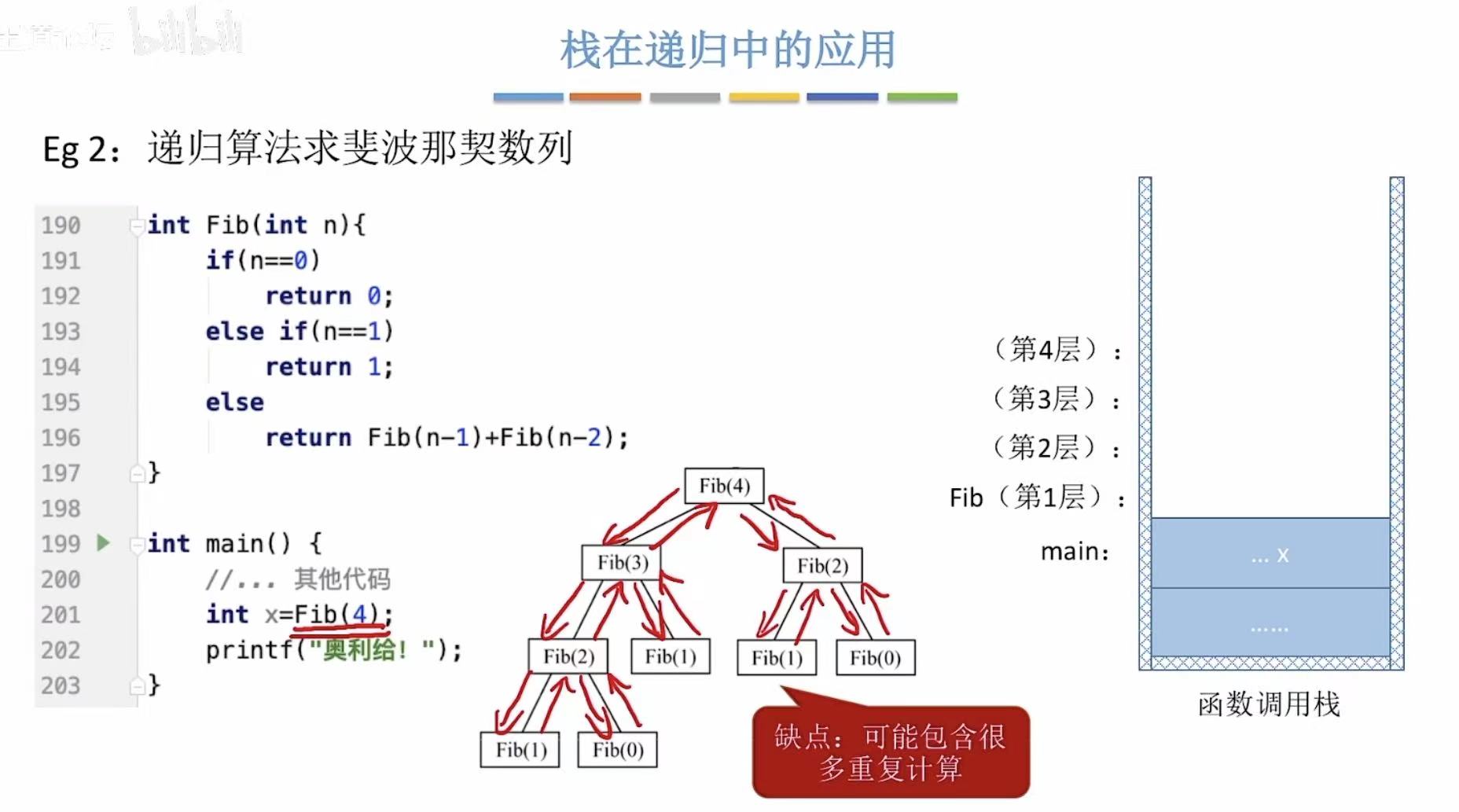
4.3 小结
队列
具体应用会在后续详细学习。
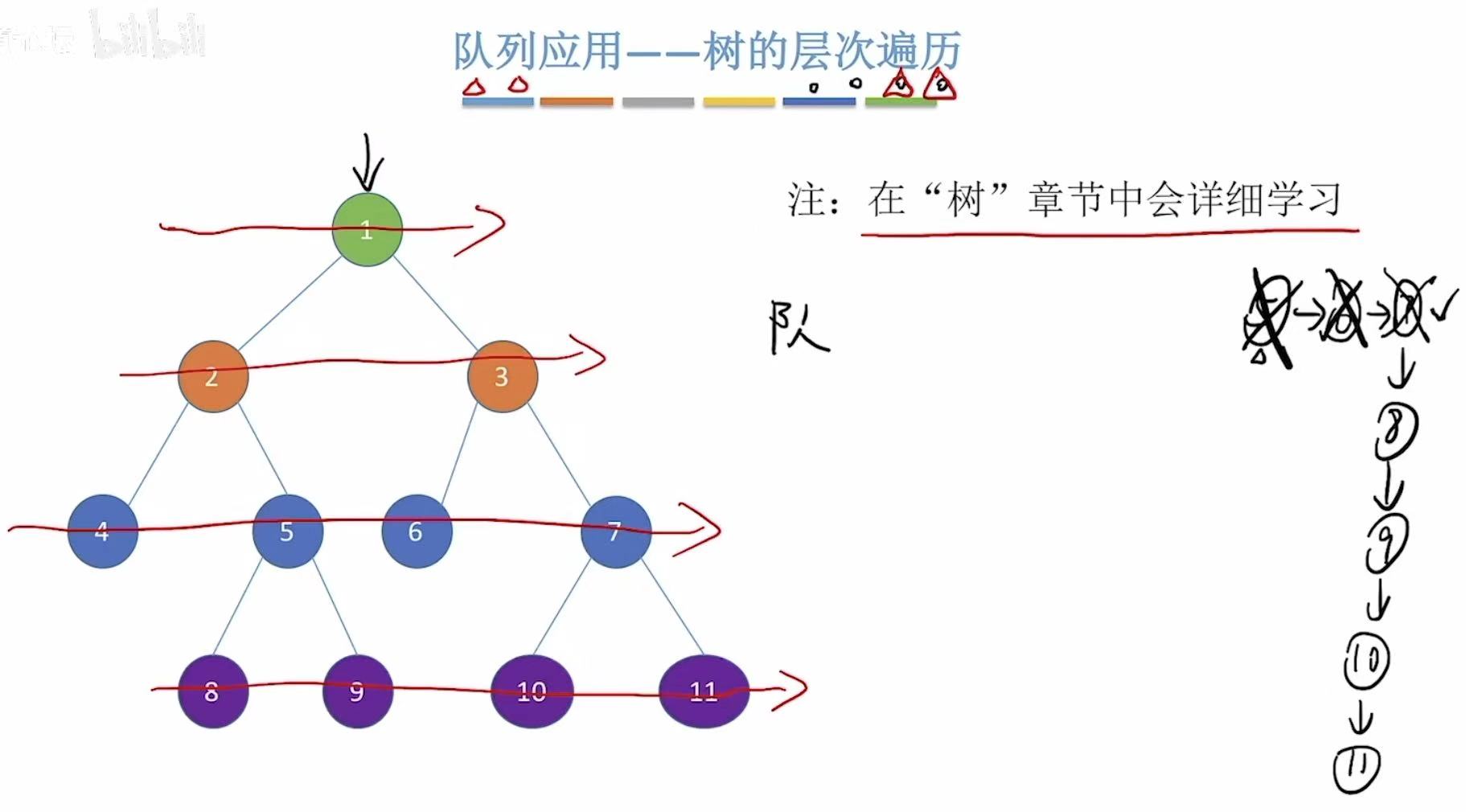
1. 树的层次遍历
先进先出:
- 先访问根节点(第1层)
- 再访问它的两个子节点(第2层)
- 然后访问第2层所有节点的子节点(第3层)
- 依此类推
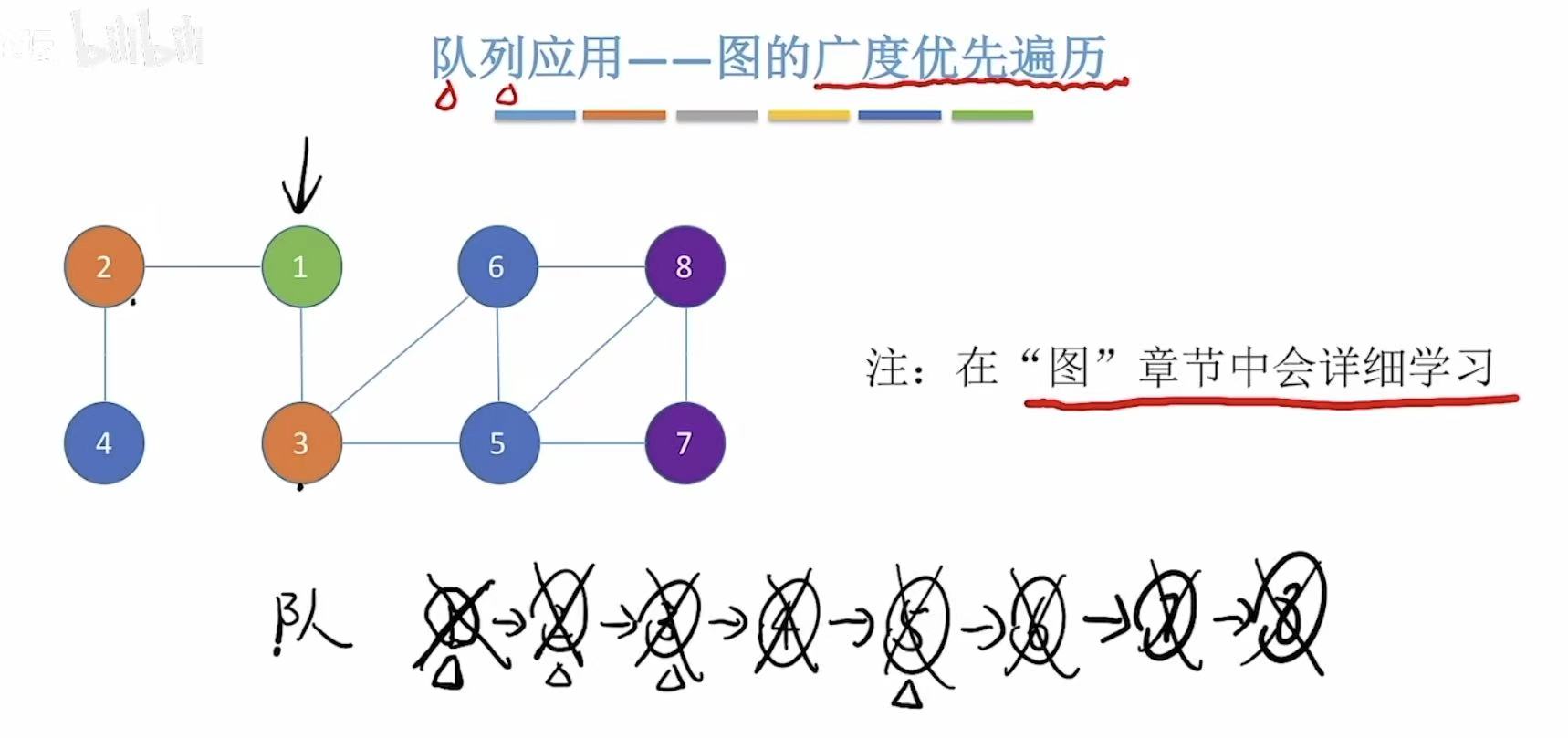
2. 图的广度优先遍历
先进先出:
- 先访问起点(1)
- 再访问它的所有邻居(2,3)
- 然后访问第1层所有节点的邻居(2-->4,3-->5,6)
- 依此类推
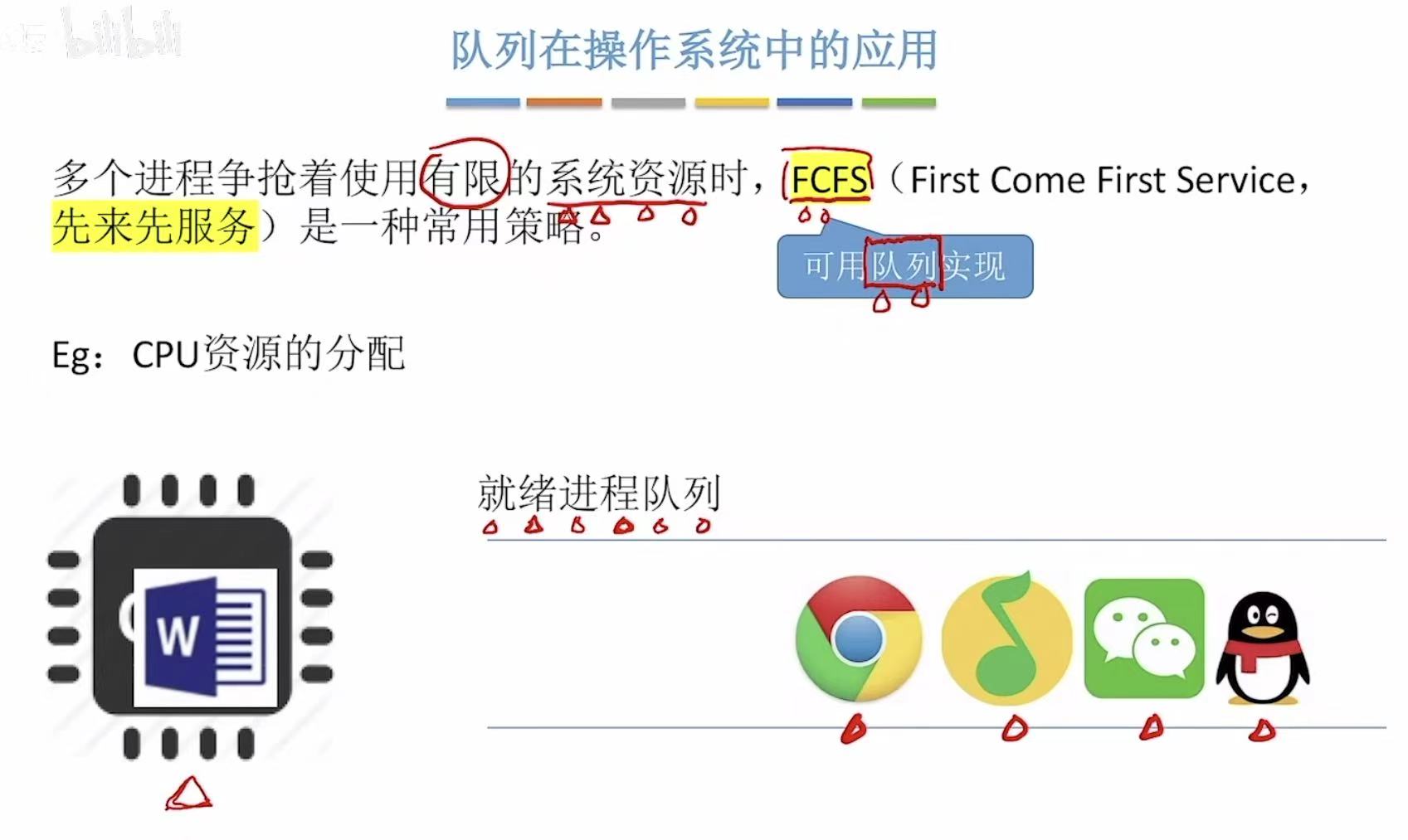
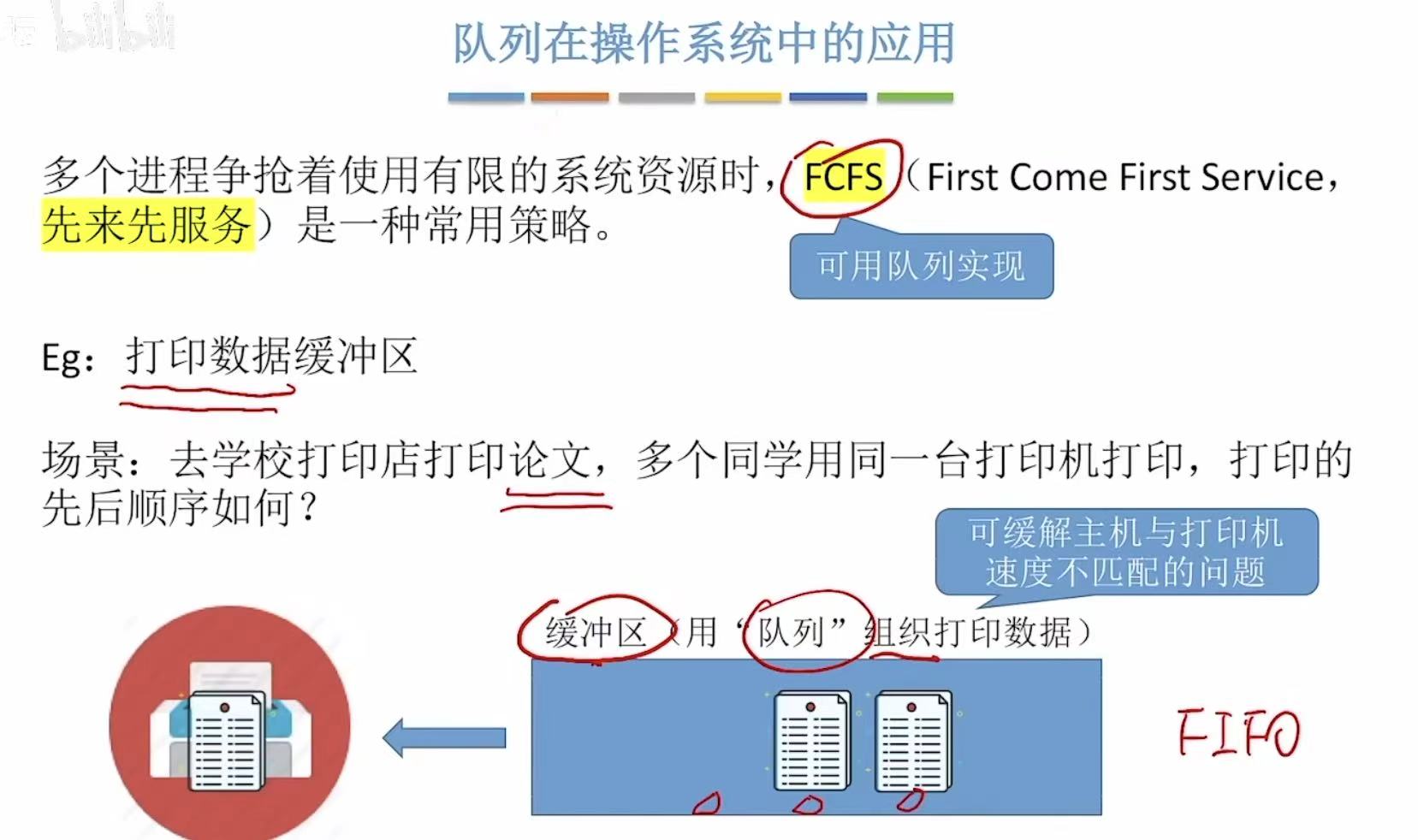
3. 在操作系统中的应用
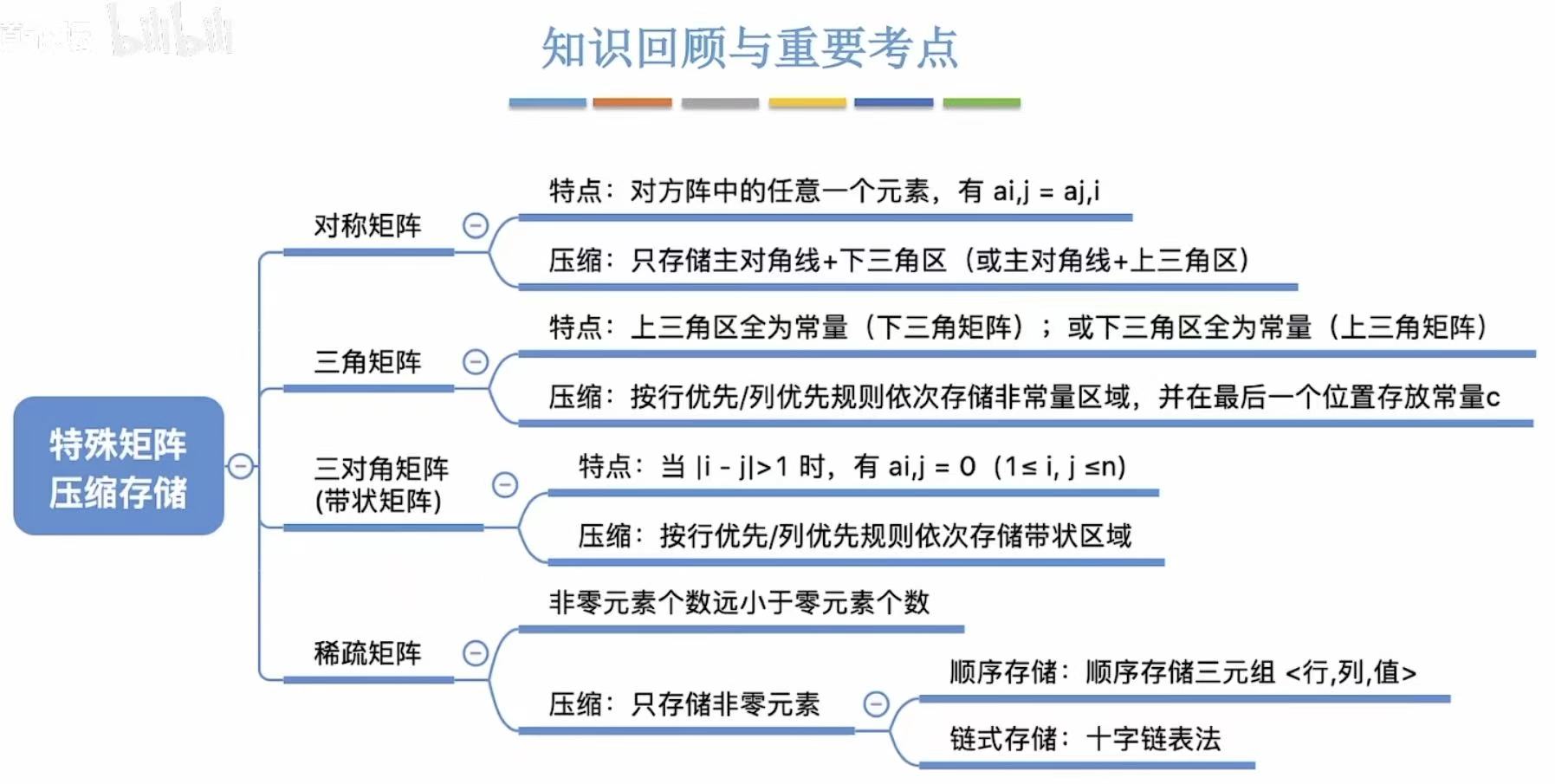
矩阵的压缩存储
涉及线性代数。
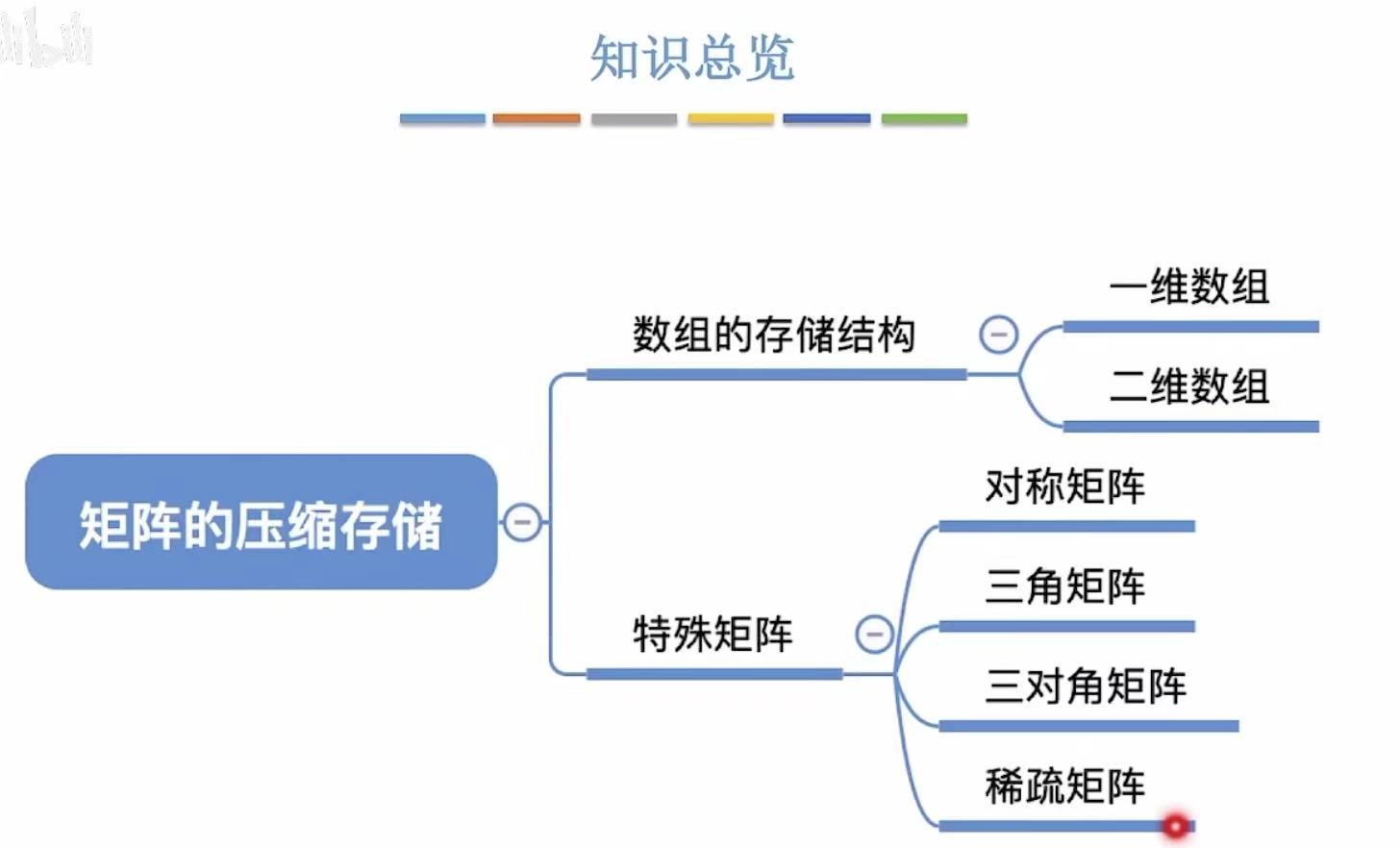
1. 数组的存储结构
1.1 一维数组的存储结构

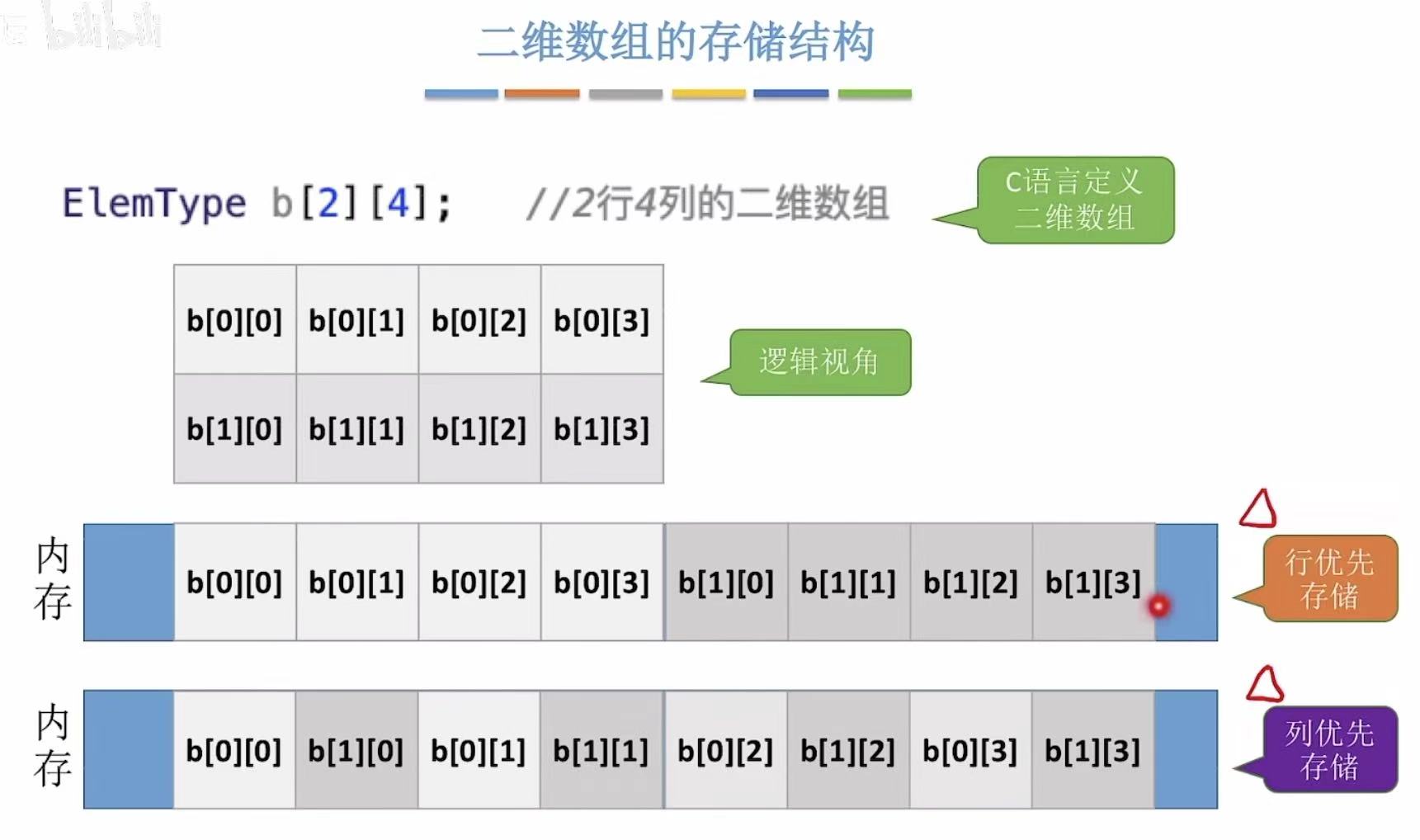
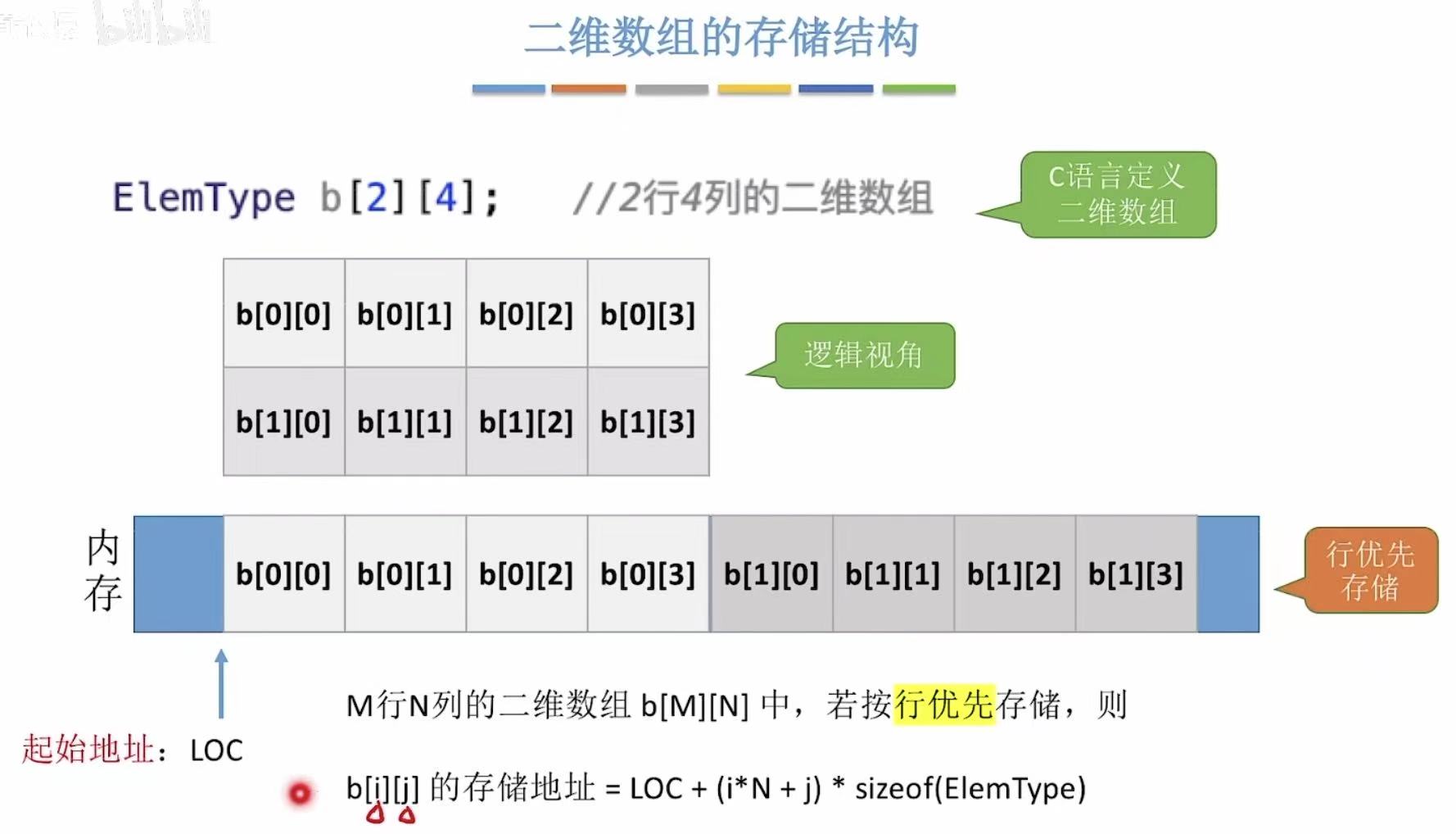
1.2 二维数组的存储结构
分为行优先 和列优先 。

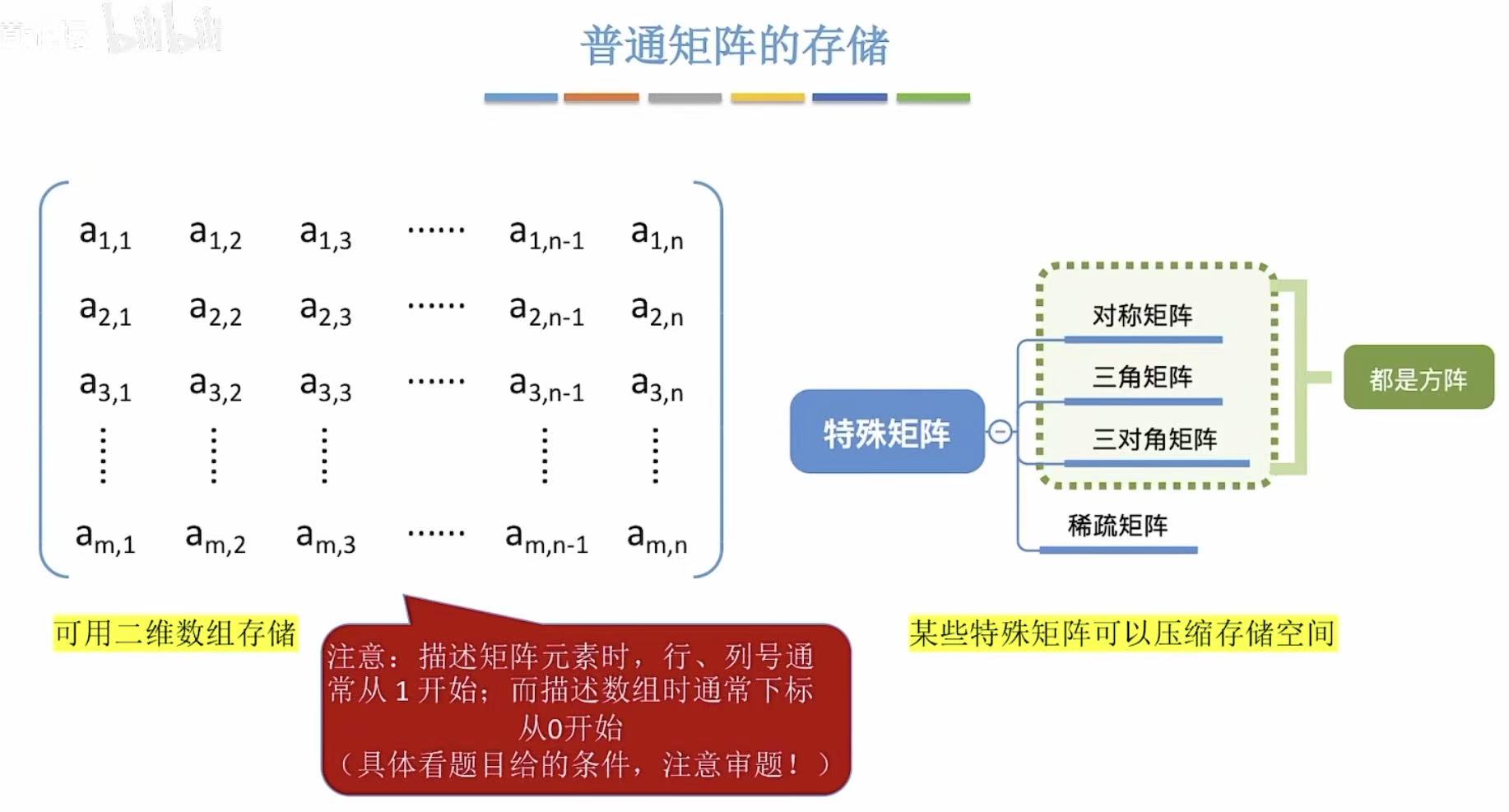
2. 矩阵的存储结构
2.1 普通矩阵
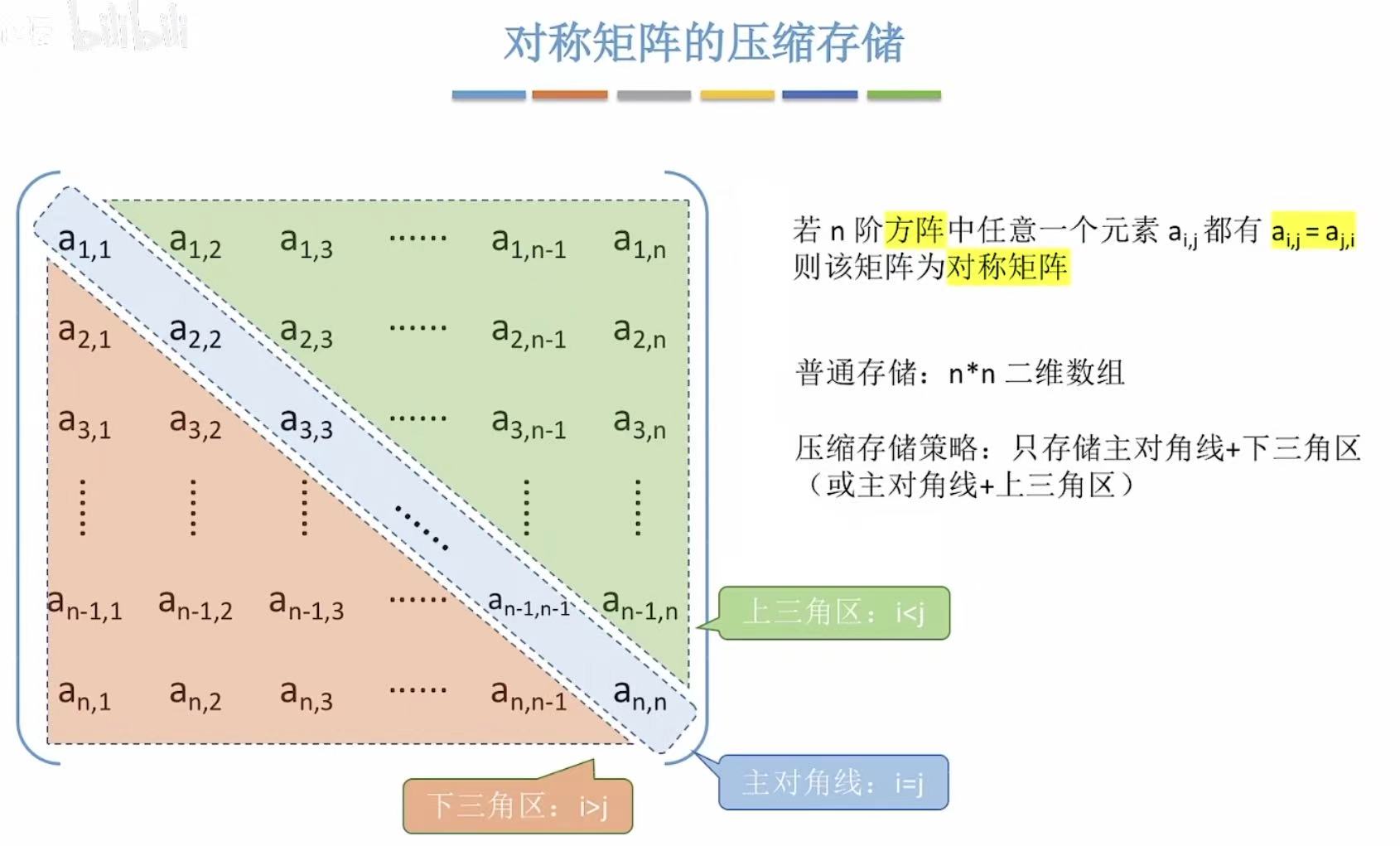
2.2 对称矩阵
对称 :上下两个三角区的数据是重复的,所以就可以节约一个三角区的空间。
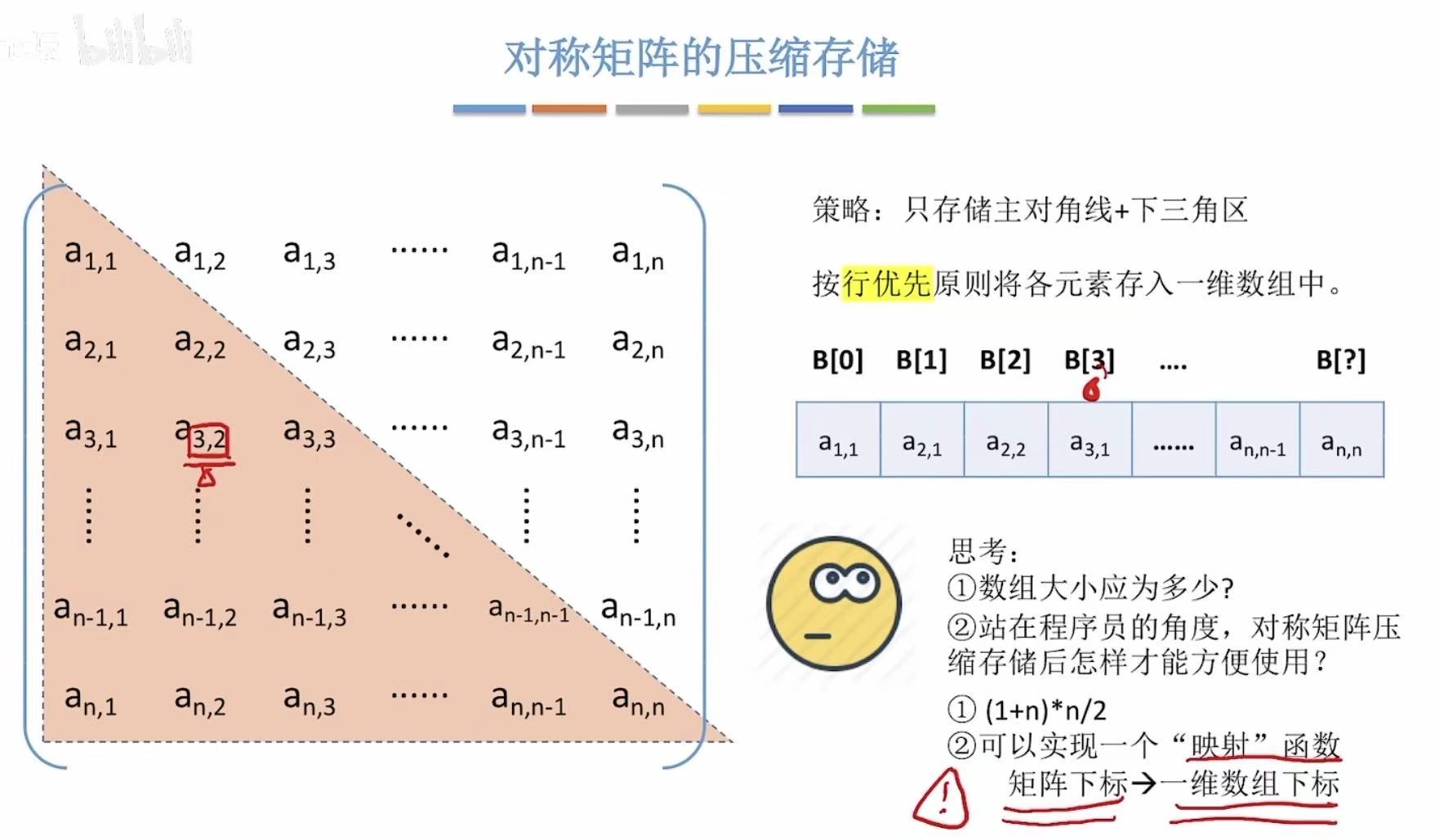
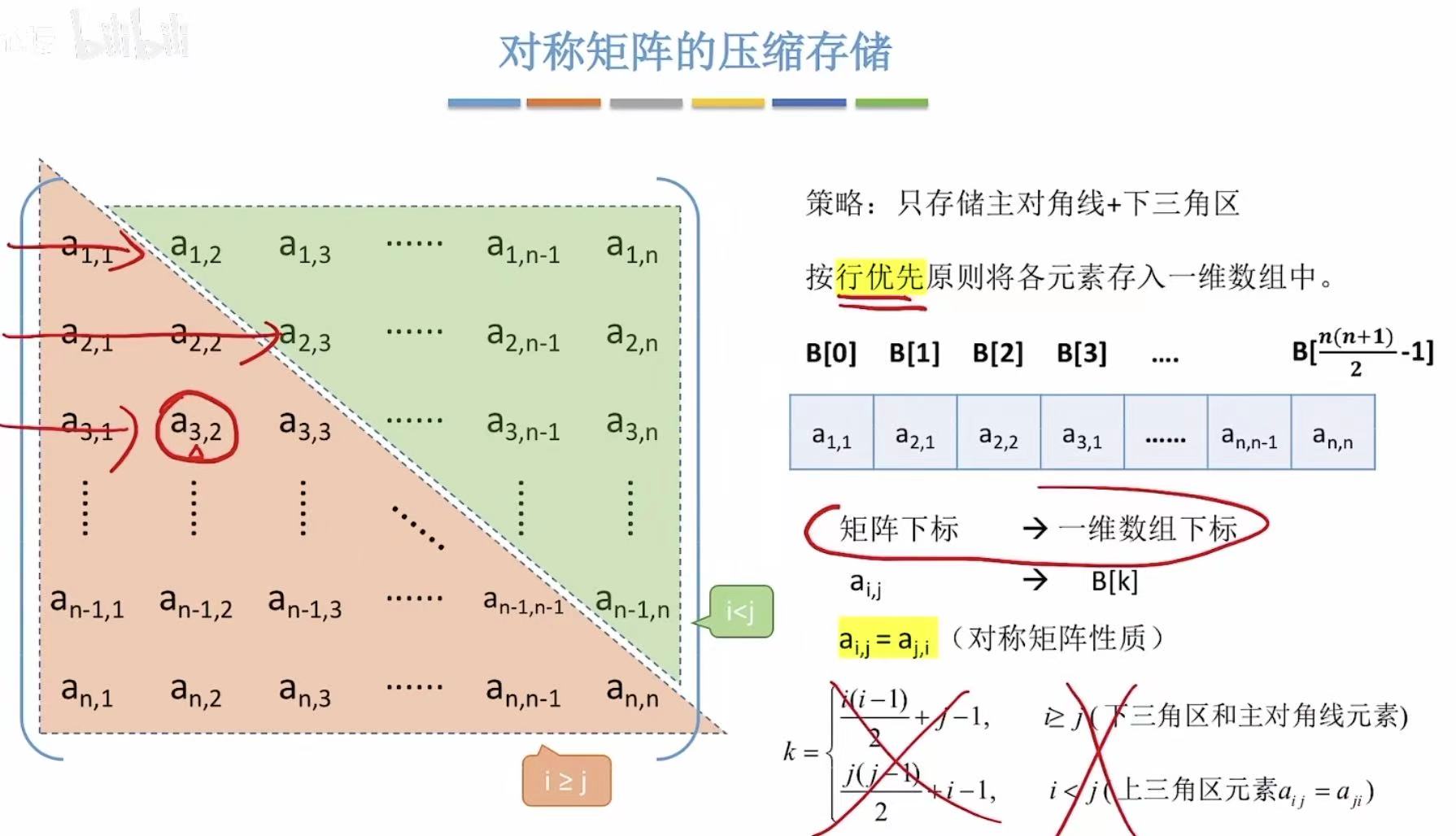
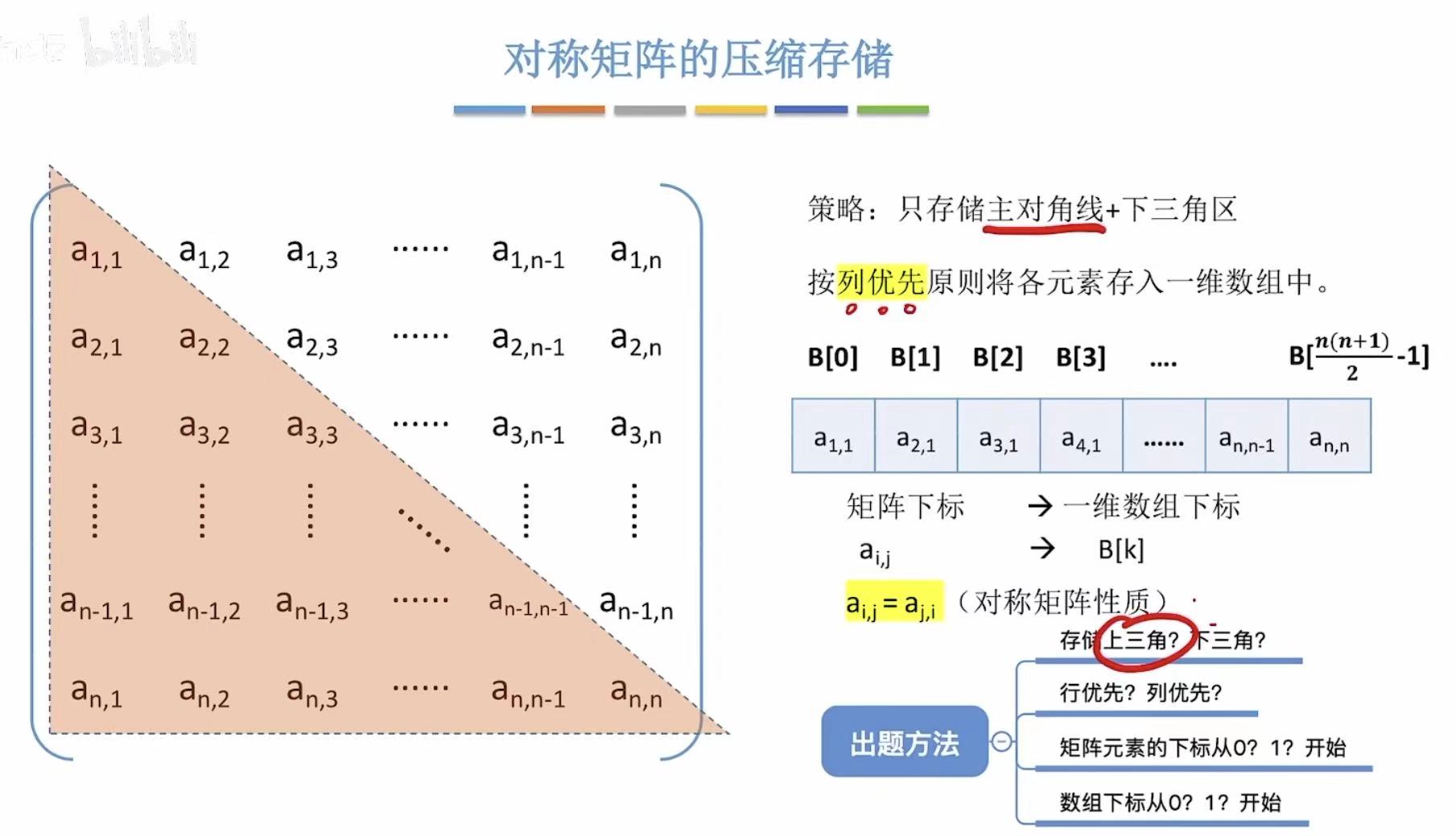
2.3 三角矩阵
三角 :上三角区或下三角区都是同一个元素,所以也可以省略出一个三角区的空间。
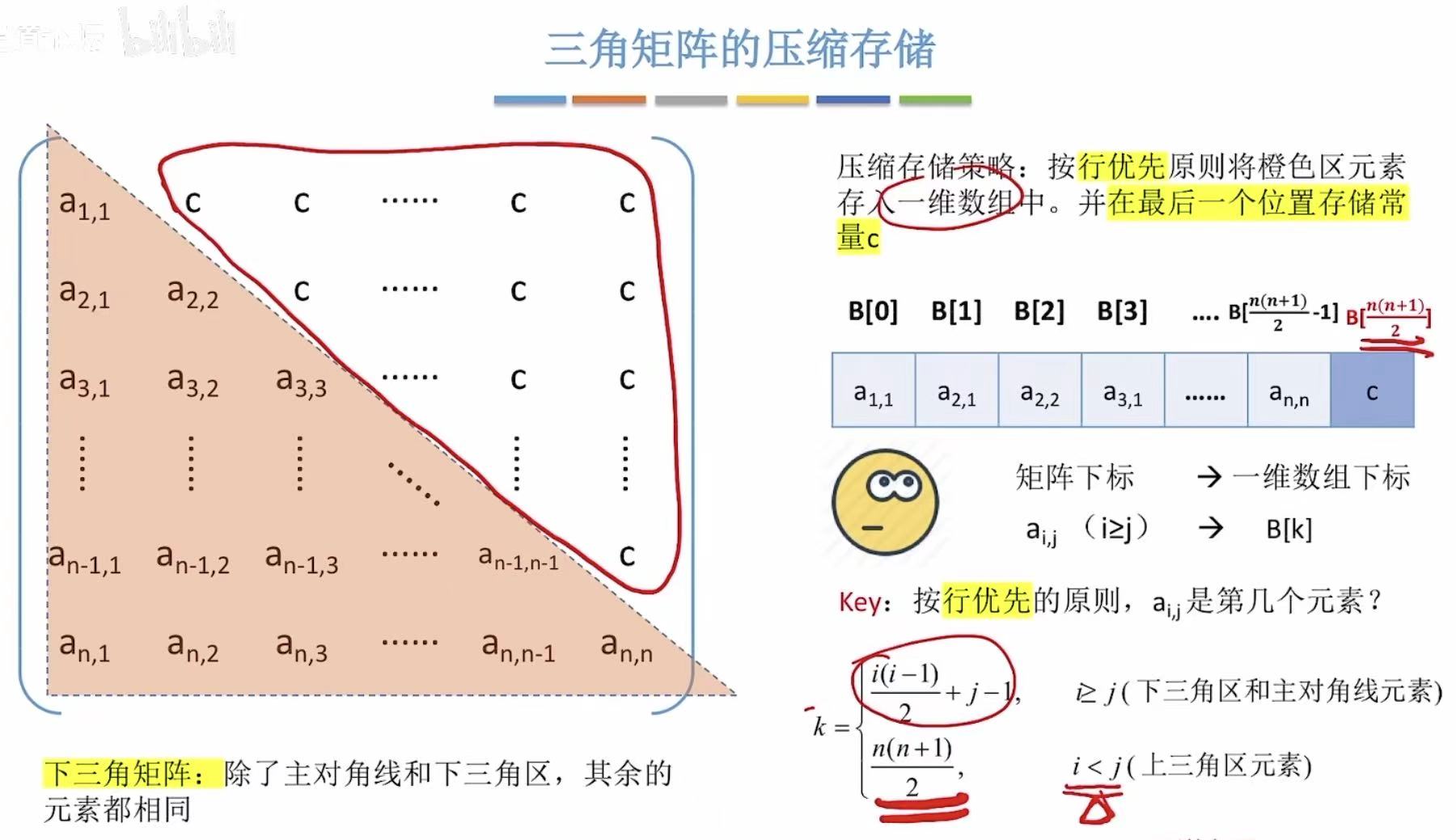
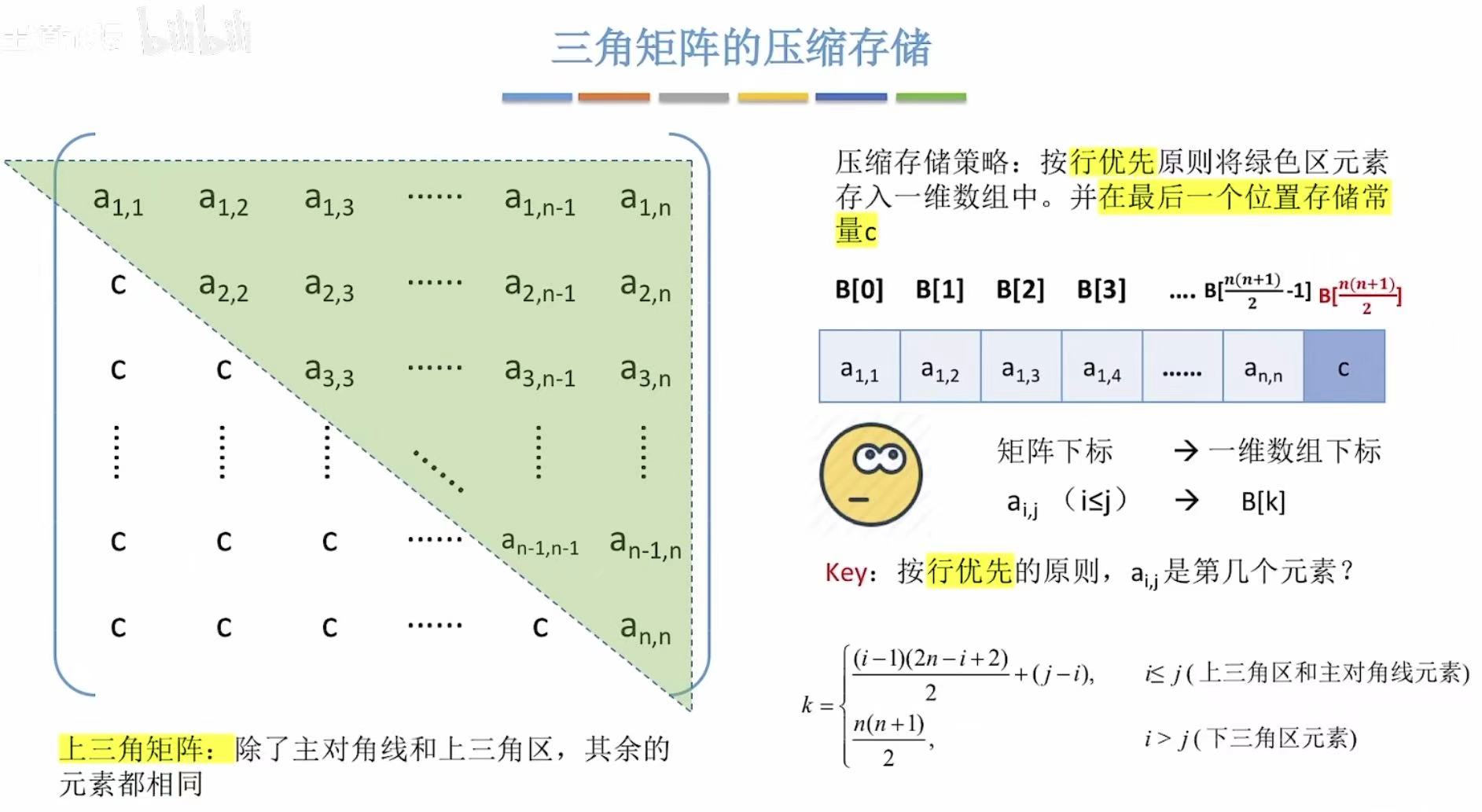
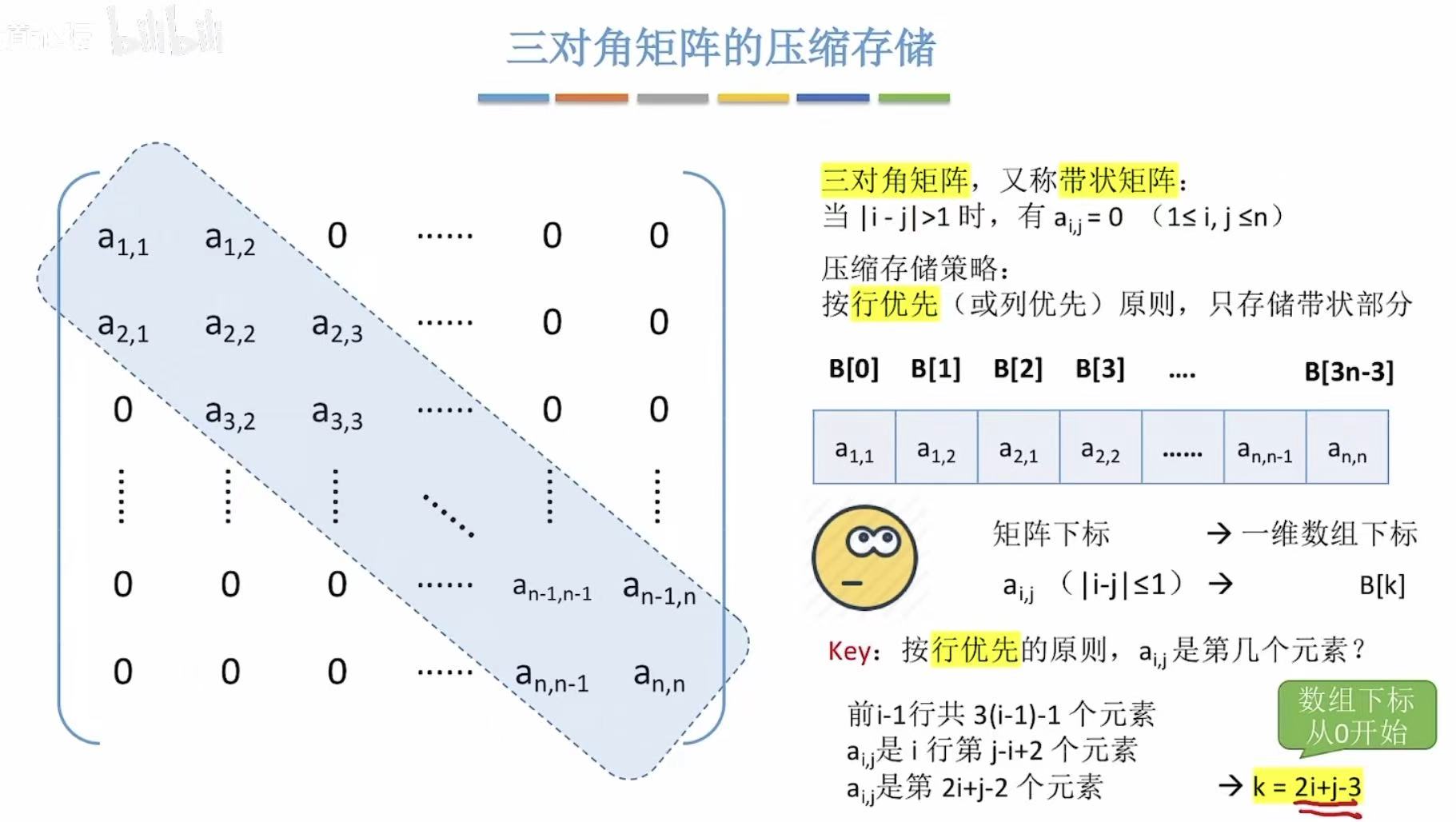
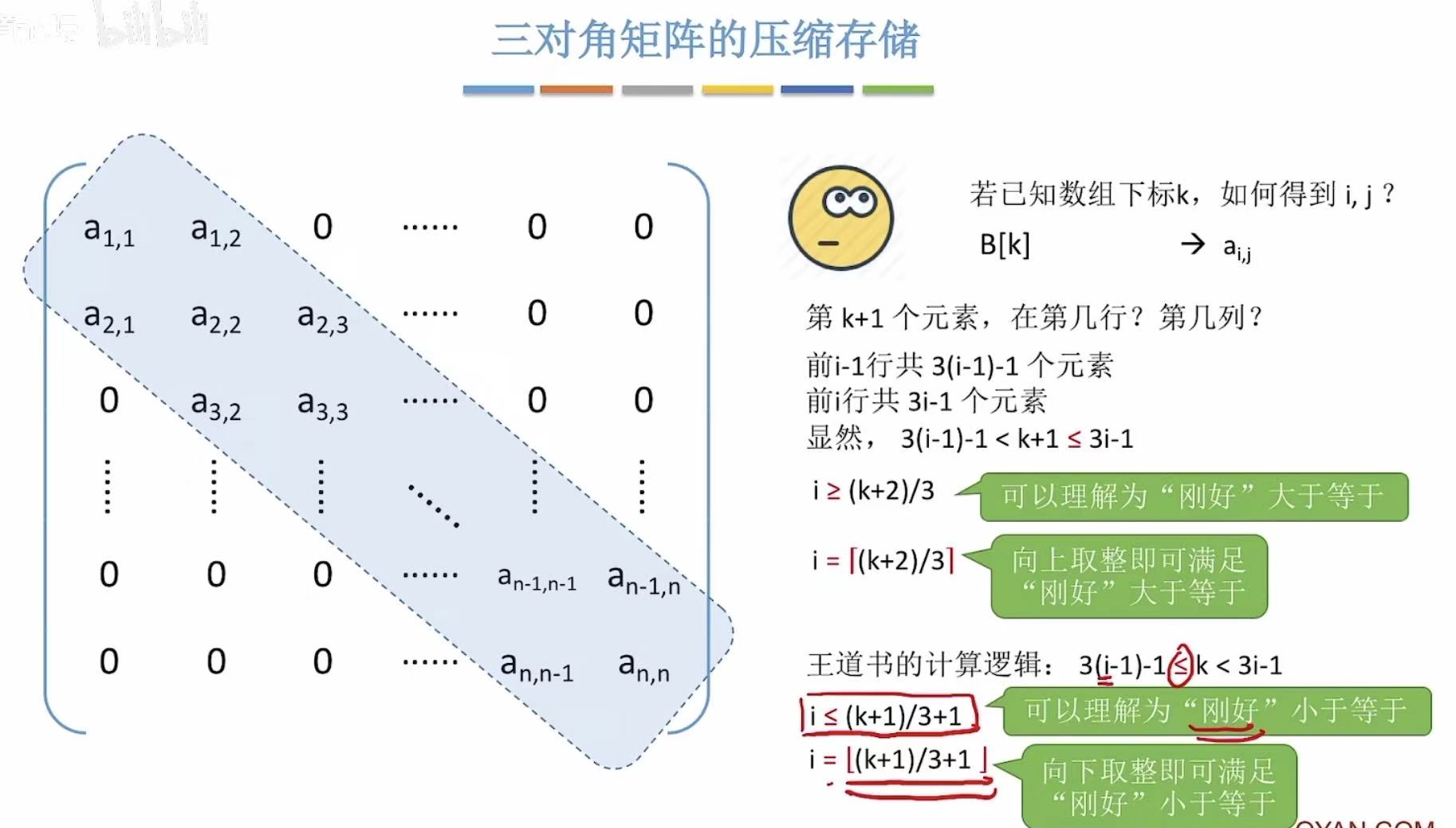
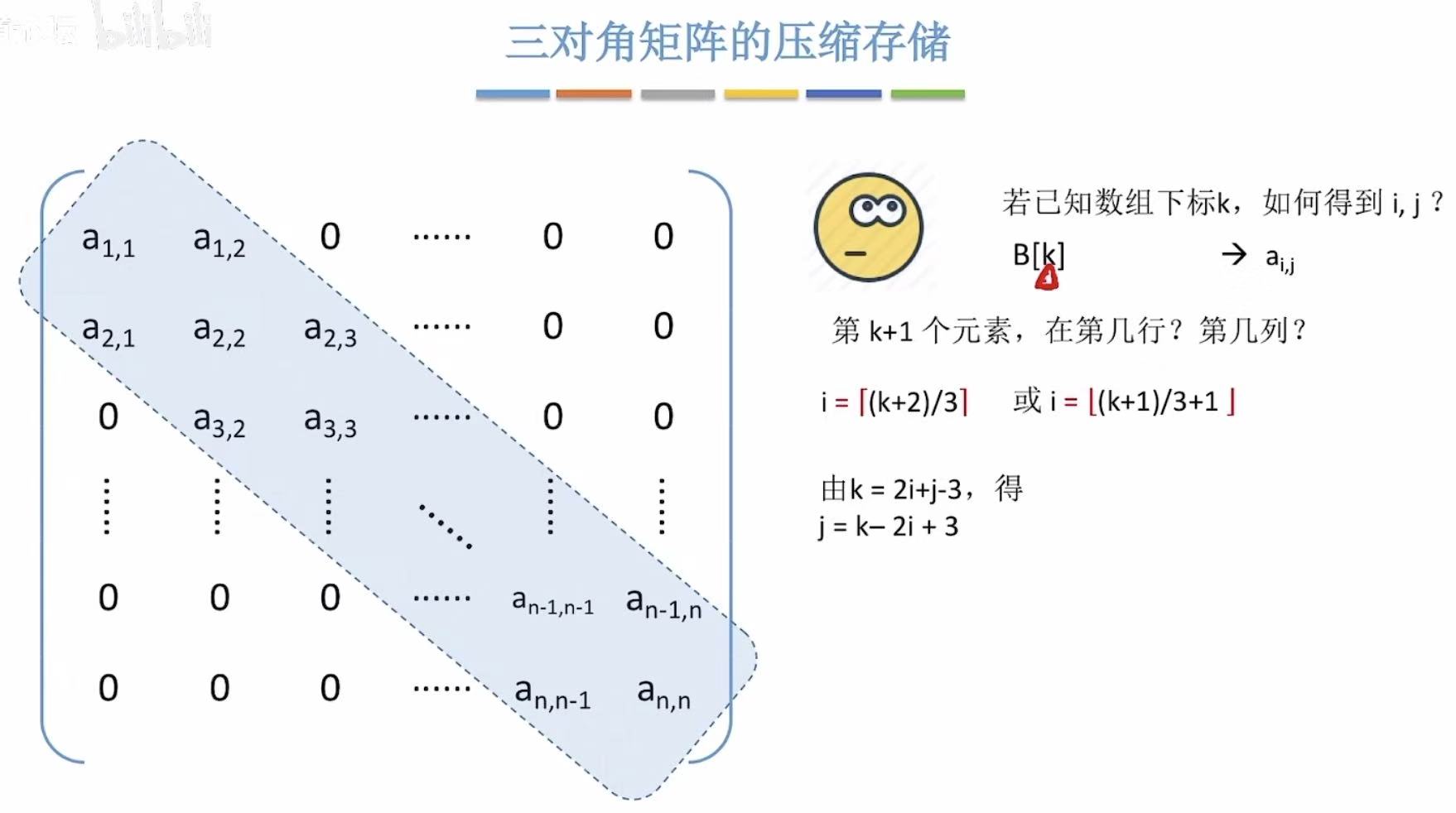
2.4 带状矩阵
带状 :除了带状的部分,其余位置都是0,所以也可以省略出很多空间。
2.5 稀疏矩阵
稀疏 :只有少部分位置有有效数据,所以可以按位置排出来,其余空间就可以被节约下来了。
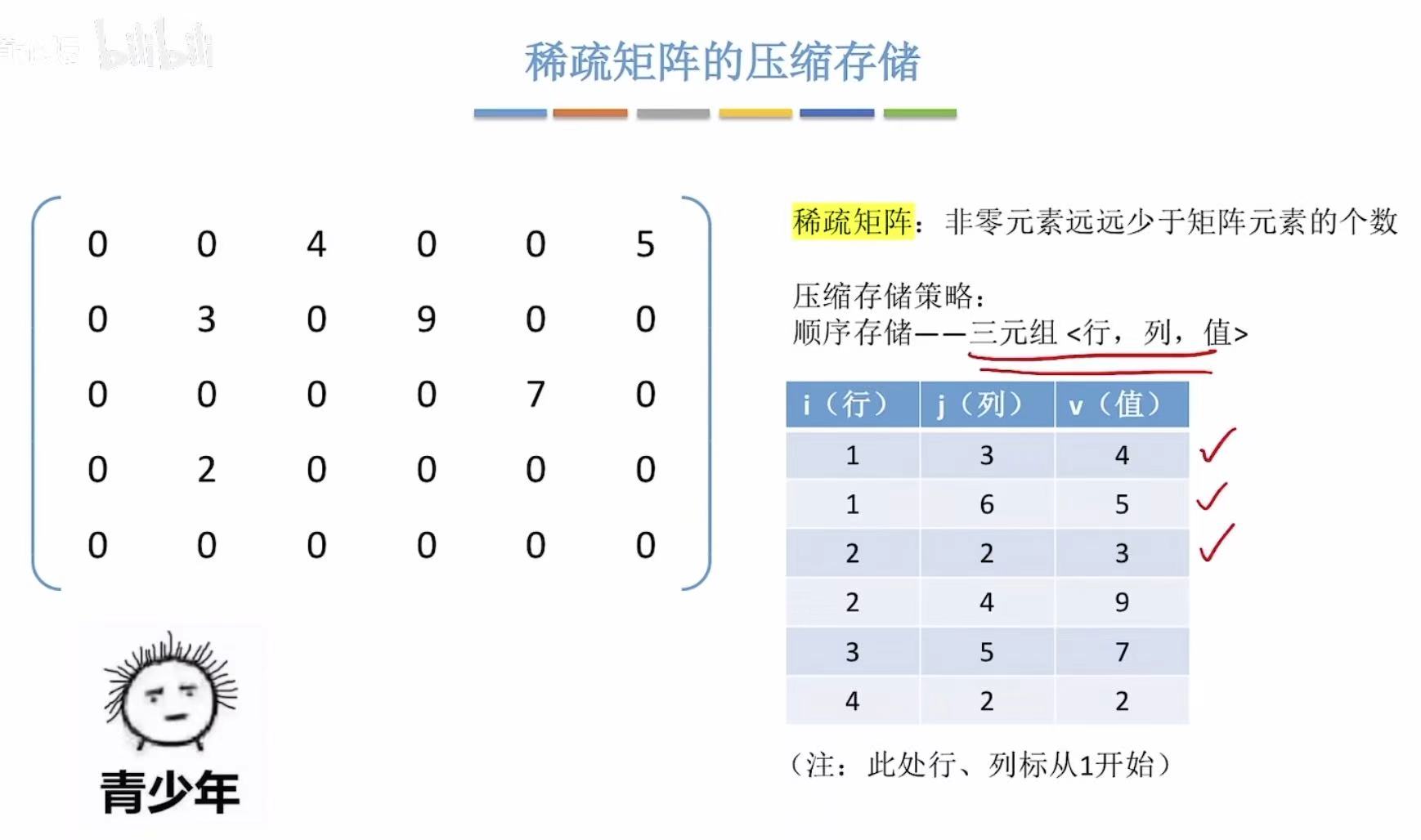
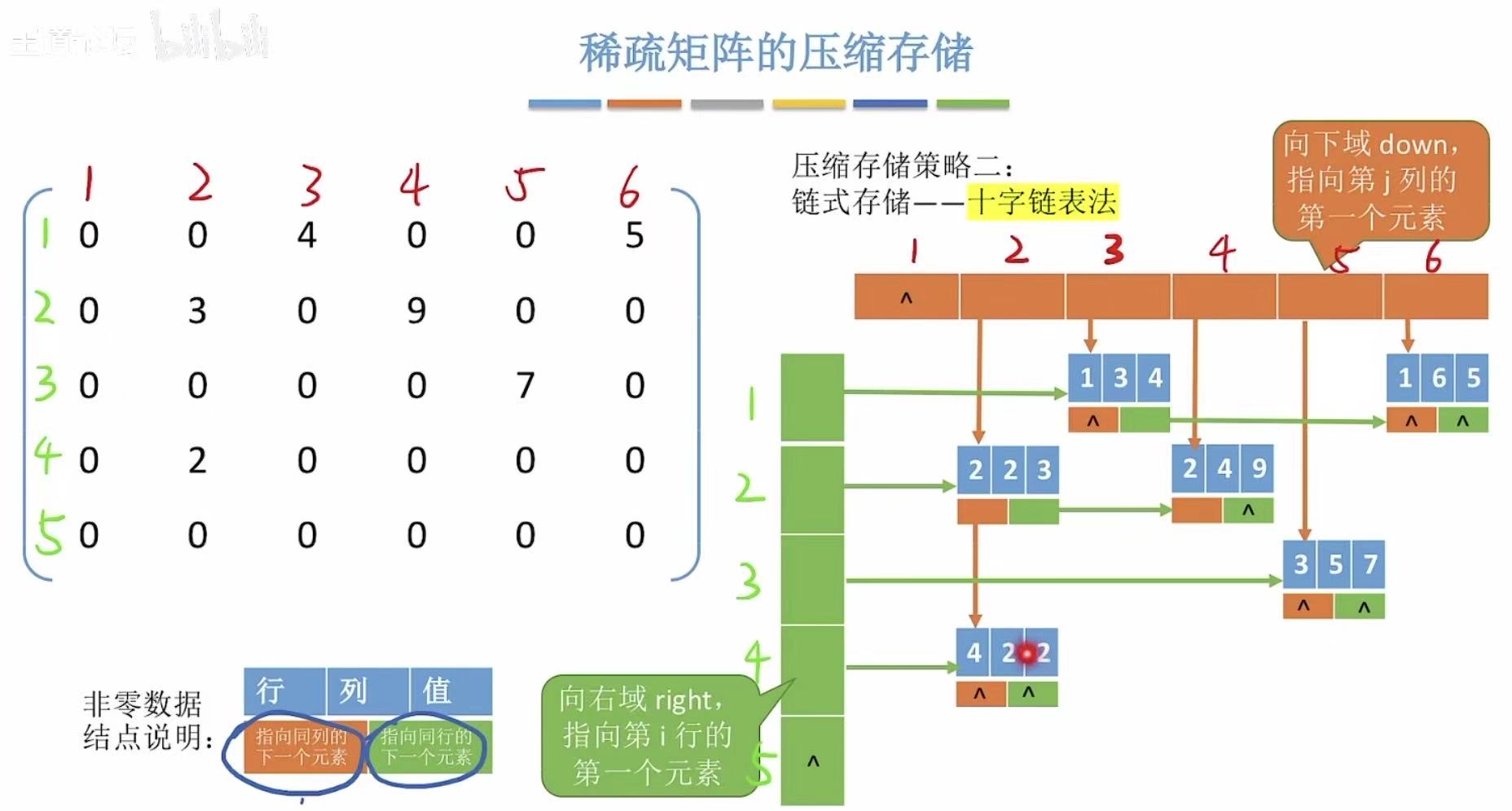
2.6 小结