CNN卷积神经网络完全入门指南:从零开始理解卷积、池化与激活函数
本文基于CS231n Lecture 5,用大量实例和可视化帮助深度学习初学者彻底掌握CNN核心理论。
一、为什么需要CNN?
在传统的全连接神经网络中,如果我们要识别一张猫的图片,需要把整张图片展平成一维向量。比如一张200×200的彩色图片会变成200×200×3=120,000个数字输入到网络中。
这样做有两个严重问题:
- 丢失空间信息:像素之间的位置关系被完全破坏
- 参数量爆炸:第一层隐藏层如果有1000个神经元,就需要120,000×1,000=1.2亿个参数!
CNN的核心思想:
- 保留图像的空间结构
- 利用图像的局部性(相邻像素关系密切)
- 利用图像的重复性(同样的特征可能出现在不同位置)
二、卷积(Convolution):CNN的灵魂
2.1 什么是卷积?
卷积就是用一个小的**过滤器(filter)或称卷积核(kernel)**在图像上滑动,通过逐元素相乘求和来提取特征。
2.2 卷积计算实例
假设我们有一张5×5的灰度图像:
1 2 3 0 1
0 1 2 3 1
1 0 1 2 0
2 1 0 1 3
1 2 1 0 2使用一个3×3的过滤器(用于检测垂直边缘):
-1 0 1
-1 0 1
-1 0 1步骤1: 将过滤器放在图像左上角的3×3区域
1 2 3
0 1 2
1 0 1步骤2: 逐元素相乘再求和
(-1)×1 + 0×2 + 1×3 = -1 + 0 + 3 = 2
(-1)×0 + 0×1 + 1×2 = 0 + 0 + 2 = 2
(-1)×1 + 0×0 + 1×1 = -1 + 0 + 1 = 0
总和 = 2 + 2 + 0 = 4(这是输出特征图的第一个值)步骤3: 滑动过滤器(stride=1),继续计算下一个位置
重复这个过程,最终得到一个3×3的特征图(feature map)。
2.3 卷积的关键参数
(1) 过滤器大小(Filter Size)
- 常用尺寸:3×3, 5×5, 7×7
- 小过滤器(3×3):捕捉局部细节,现代网络首选
- 大过滤器(7×7):捕捉更大范围的模式,但参数多
(2) 步长(Stride)
- Stride=1:过滤器每次移动1个像素
- Stride=2:过滤器每次移动2个像素(输出尺寸更小)
(3) 填充(Padding)
问题: 卷积操作会使输出尺寸缩小
- 输入5×5,使用3×3卷积(无填充)→ 输出3×3
解决方案: 在图像边缘填充0(zero padding)
填充后的图像:
0 0 0 0 0 0 0
0 1 2 3 0 1 0
0 0 1 2 3 1 0
0 1 0 1 2 0 0
0 2 1 0 1 3 0
0 1 2 1 0 2 0
0 0 0 0 0 0 0填充类型:
- Same padding:填充使输出和输入尺寸相同
- Valid padding:不填充,输出尺寸缩小
(4) 输出尺寸计算公式
输出大小 = ⌊(输入大小 - 过滤器大小 + 2×Padding) / Stride⌋ + 1实例计算:
-
输入:32×32
-
过滤器:5×5
-
Padding:2
-
Stride:1
输出 = (32 - 5 + 2×2) / 1 + 1 = (32 - 5 + 4) / 1 + 1 = 32
输出尺寸为32×32(与输入相同)
2.4 为什么卷积如此有效?
参数共享(Parameter Sharing)
- 全连接层:每个神经元都有独立的参数
- 卷积层:同一个过滤器在整个图像上共享参数
例子: 一个3×3的过滤器只有9个参数,但可以检测整张图像中的所有垂直边缘!
局部连接(Local Connectivity)
- 每个神经元只连接到输入的一小块区域(感受野 receptive field)
- 符合视觉系统的局部性原理:识别一个物体不需要同时看整张图
平移不变性(Translation Invariance)
- 无论猫出现在图像的哪个位置,同一个过滤器都能检测到
- 这是通过参数共享自然获得的特性
三、池化(Pooling):降维与增强鲁棒性
3.1 为什么需要池化?
- 减少参数量和计算量:降低特征图的空间维度
- 增强平移不变性:即使特征位置稍微移动,池化后的结果基本不变
- 提取主导特征:保留最重要的信息
3.2 最大池化(Max Pooling)
最大池化是最常用的池化方式,它从每个区域中选取最大值。
实例: 2×2 Max Pooling,stride=2
输入特征图(4×4):
1 3 2 4
5 6 7 8
3 2 1 0
1 2 3 4将其分成4个不重叠的2×2区域:
区域1(左上): | 1 3 | → max = 6
| 5 6 |
区域2(右上): | 2 4 | → max = 8
| 7 8 |
区域3(左下): | 3 2 | → max = 3
| 1 2 |
区域4(右下): | 1 0 | → max = 4
| 3 4 |输出特征图(2×2):
6 8
3 43.3 平均池化(Average Pooling)
取每个区域的平均值,常用于网络最后的全局池化层。
使用同样的输入:
区域1: (1+3+5+6)/4 = 3.75
区域2: (2+4+7+8)/4 = 5.25
区域3: (3+2+1+2)/4 = 2
区域4: (1+0+3+4)/4 = 23.4 池化的关键特性
- 没有可学习参数:池化操作是固定的
- 减少空间维度:通常使高和宽减半
- 保留通道数:如果输入有64个通道,输出也是64个通道
四、激活函数(Activation Functions):引入非线性
4.1 为什么需要激活函数?
核心原因: 没有激活函数,多层神经网络本质上还是线性变换。
数学证明:
第1层:y1 = W1·x
第2层:y2 = W2·y1 = W2·(W1·x) = (W2·W1)·x
结论:两层线性变换等价于一层线性变换!激活函数的作用: 引入非线性,使网络能够学习复杂的模式和决策边界。
4.2 ReLU(整流线性单元)------ 最常用
定义:
ReLU(x) = max(0, x)实例:
输入: [-2, -1, 0, 1, 2]
输出: [ 0, 0, 0, 1, 2]优点:
- 计算简单:只需比较和选择
- 缓解梯度消失:正数部分梯度恒为1
- 稀疏激活:约50%的神经元输出为0,使网络更高效
缺点:
- Dead ReLU问题:如果神经元的输入总是负数,它将永远输出0,无法更新
4.3 Leaky ReLU
定义:
Leaky ReLU(x) = max(0.01x, x)改进: 负数部分保留一个小的梯度(0.01),避免Dead ReLU问题。
实例:
输入: [-2, -1, 0, 1, 2]
输出: [-0.02, -0.01, 0, 1, 2]4.4 Sigmoid 和 Tanh
Sigmoid函数
定义:
σ(x) = 1 / (1 + e^(-x))- 输出范围:(0, 1)
- 常用场景:二分类问题的输出层
Tanh函数
定义:
tanh(x) = (e^x - e^(-x)) / (e^x + e^(-x))- 输出范围:(-1, 1)
- 优于Sigmoid:输出以0为中心
为什么在隐藏层少用?
- 梯度消失严重:在x很大或很小时,梯度接近0
- 计算复杂:涉及指数运算
五、完整CNN架构示例:LeNet-5
LeNet-5是Yann LeCun在1998年提出的经典CNN架构,用于手写数字识别。
网络结构
输入层: 32×32×1(灰度图像)
↓
卷积层1 (Conv1):
- 6个 5×5 过滤器
- 输出: 28×28×6
↓
激活函数: ReLU
↓
池化层1 (MaxPool1):
- 2×2 池化窗口
- 输出: 14×14×6
↓
卷积层2 (Conv2):
- 16个 5×5 过滤器
- 输出: 10×10×16
↓
激活函数: ReLU
↓
池化层2 (MaxPool2):
- 2×2 池化窗口
- 输出: 5×5×16
↓
展平层 (Flatten):
- 5×5×16 = 400维向量
↓
全连接层1 (FC1):
- 400 → 120
↓
激活函数: ReLU
↓
全连接层2 (FC2):
- 120 → 84
↓
激活函数: ReLU
↓
输出层 (FC3):
- 84 → 10(对应0-9十个数字)特征层次的演变
| 层级 | 空间维度 | 通道数 | 学习的特征 |
|---|---|---|---|
| 输入 | 32×32 | 1 | 原始像素 |
| Conv1后 | 28×28 | 6 | 边缘、基本线条 |
| Pool1后 | 14×14 | 6 | 下采样的边缘 |
| Conv2后 | 10×10 | 16 | 纹理、简单形状 |
| Pool2后 | 5×5 | 16 | 下采样的形状 |
| FC层 | - | - | 高级语义特征 |
关键观察:
- 空间维度逐渐减小:32→28→14→10→5
- 通道数逐渐增加:1→6→16
- 特征从低级到高级:像素→边缘→纹理→部件→物体
六、直觉理解CNN
卷积层:层次化的特征检测器
想象CNN就像一个自动学习的视觉系统:
第1层卷积: 学习检测基础视觉元素
- 水平边缘检测器
- 垂直边缘检测器
- 对角线检测器
- 颜色变化检测器
第2层卷积: 组合第1层的特征
- 检测纹理(由多个边缘组成)
- 检测简单几何形状(圆、方、角)
第3层卷积: 检测物体部件
- 眼睛
- 轮子
- 窗户
第4层及更深: 检测完整物体
- 人脸
- 汽车
- 房屋
池化层:智能降采样
池化就像"缩略图":
- 保留图像中最重要的信息
- 丢弃精确位置信息
- 使网络对小的位移更鲁棒
类比: 你看一张猫的照片
- 不需要记住每根胡须的精确位置
- 只需要知道"这里有胡须"
- 池化做的就是这件事
激活函数:决策的非线性
线性系统的限制:
如果只能画直线,无法分隔复杂的数据分布ReLU的作用:
允许网络学习复杂的、非线性的决策边界
就像从"只能画直线"升级到"能画任意曲线"七、CNN设计的黄金法则
法则1:用小卷积核堆叠
现代网络首选 3×3 卷积核
原因:
- 两个3×3卷积的感受野 = 一个5×5卷积
- 但参数量更少:2×(3×3) = 18 vs 5×5 = 25
- 引入更多非线性(两个ReLU vs 一个ReLU)
法则2:逐层增加通道数,减小空间尺寸
典型模式:
64×64×64 → 32×32×128 → 16×16×256 → 8×8×512直觉:
- 早期层:关注空间细节(高分辨率,少通道)
- 后期层:关注语义信息(低分辨率,多通道)
法则3:标准组合
卷积块的标准配置:
Conv → BatchNorm → ReLU → (可选)Pool为什么这样有效:
- BatchNorm:稳定训练,加速收敛
- ReLU:简单高效的非线性
- Pool:控制参数量
法则4:用全局池化替代全连接层
传统方式:
7×7×512 → Flatten → FC(25088 → 1000)
参数量:25,088,000现代方式:
7×7×512 → Global Average Pooling → 1×1×512 → FC(512 → 1000)
参数量:512,000优势:
- 大幅减少参数,防止过拟合
- 对输入尺寸更灵活
八、核心要点总结
三大核心操作对比
| 操作 | 主要作用 | 关键参数 | 是否有可学习参数 |
|---|---|---|---|
| 卷积 | 特征提取 | 卷积核大小、数量、stride、padding | ✅ 是(卷积核权重) |
| 池化 | 降维、增强鲁棒性 | 池化大小、stride | ❌ 否 |
| 激活函数 | 引入非线性 | 无(ReLU无参数) | ❌ 否 |
记忆口诀
卷积三要素: 核、步、填(kernel, stride, padding)
池化两要素: 窗、步(window, stride)
激活首选: ReLU简单又高效
一、什么是感受野?
1.1 核心定义
感受野(Receptive Field):神经网络中某一层的一个神经元,在原始输入图像上能"看到"的区域大小。
1.2 全连接 vs 卷积神经网络
全连接神经网络
输入层(9个神经元) 隐藏层(4个神经元)
● ●───┐
● ● │
● ● ├─ 每个隐藏层神经元
● ─────────全部连接────→ ● │ 都连接到所有输入
● ↑ │
● │ │
● └───┘
● 参数量 = 9×4 = 36个
●
问题:
- 参数太多
- 忽略空间结构
- 无法共享特征检测器卷积神经网络(局部连接)
输入层(3×3=9个神经元) 隐藏层神经元
● ● ● ┌─●─┐
● ● ● ──局部连接──→ │ ● │ ← 只连接左上3×3区域
● ● ● └─●─┘
感受野 = 3×3区域
参数量 = 3×3 = 9个
优势:
✓ 参数共享
✓ 保留空间结构
✓ 平移不变性二、单层卷积的感受野计算
2.1 基础示例:3×3卷积
输入图像(5×5):
┌─────────────────┐
│ 1 2 3 4 5│ 行0
│ 6 7 8 9 10│ 行1
│11 12 13 14 15│ 行2
│16 17 18 19 20│ 行3
│21 22 23 24 25│ 行4
└─────────────────┘
列0 列1 列2 列3 列43×3卷积核(stride=1, padding=0):
┌─────────┐
│ w1 w2 w3│
│ w4 w5 w6│
│ w7 w8 w9│
└─────────┘2.2 计算第一个输出神经元(位置[0,0])
卷积核覆盖的区域:
┌─────────────────┐
│[1] [2] [3] 4 5│ ← 行0-2
│[6] [7] [8] 9 10│
│[11][12][13] 14 15│
│16 17 18 19 20│
│21 22 23 24 25│
└─────────────────┘
列0-2计算过程:
输出[0,0] = w1×1 + w2×2 + w3×3 +
w4×6 + w5×7 + w6×8 +
w7×11 + w8×12 + w9×13
感受野坐标 = {(0,0), (0,1), (0,2),
(1,0), (1,1), (1,2),
(2,0), (2,1), (2,2)}
感受野大小 = 3×32.3 计算第二个输出神经元(位置[0,1])
卷积核向右移动1格(stride=1):
┌─────────────────┐
│ 1 [2] [3] [4] 5│
│ 6 [7] [8] [9] 10│
│11 [12][13][14] 15│
│16 17 18 19 20│
│21 22 23 24 25│
└─────────────────┘计算过程:
输出[0,1] = w1×2 + w2×3 + w3×4 +
w4×7 + w5×8 + w6×9 +
w7×12 + w8×13 + w9×14
感受野坐标 = {(0,1), (0,2), (0,3),
(1,1), (1,2), (1,3),
(2,1), (2,2), (2,3)}
感受野大小 = 3×3(向右移动了1格)2.4 计算中心位置的神经元(位置[1,1])
卷积核移动到中心:
┌─────────────────┐
│ 1 2 3 4 5│
│ 6 [7] [8] [9] 10│
│11 [12][13][14] 15│
│16 [17][18][19] 20│
│21 22 23 24 25│
└─────────────────┘计算过程:
输出[1,1] = w1×7 + w2×8 + w3×9 +
w4×12 + w5×13 + w6×14 +
w7×17 + w8×18 + w9×19
感受野坐标 = {(1,1), (1,2), (1,3),
(2,1), (2,2), (2,3),
(3,1), (3,2), (3,3)}
感受野大小 = 3×32.5 完整输出特征图
输出特征图(3×3):
┌─────────┐
│ a b c │ 每个位置的神经元
│ d e f │ 都有自己的3×3感受野
│ g h i │ 但位置不同
└─────────┘结论:单层3×3卷积,每个神经元的感受野都是3×3
三、两层卷积的感受野计算(核心)
3.1 网络设置
- 第1层:3×3卷积,stride=1
- 第2层:3×3卷积,stride=1
3.2 三层数据结构
【第0层】输入 【第1层】特征图 【第2层】特征图
7×7 5×5 3×3
0 1 2 3 4 5 6 A B C D E α β γ
1 2 3 4 5 6 7 F G H I J δ ε ζ
2 3 4 5 6 7 8 K L M N O η θ ι
3 4 5 6 7 8 9 P Q R S T
4 5 6 7 8 9 0 U V W X Y
5 6 7 8 9 0 1
6 7 8 9 0 1 23.3 第1层神经元的感受野(在第0层)
神经元 A 的感受野
┌─────────────┐
│[0][1][2] 3 4 5 6│ 行0-2
│[1][2][3] 4 5 6 7│
│[2][3][4] 5 6 7 8│
│ 3 4 5 6 7 8 9│
│ 4 5 6 7 8 9 0│
│ 5 6 7 8 9 0 1│
│ 6 7 8 9 0 1 2│
└─────────────┘
列0-2
A = f(输入[0-2行, 0-2列])
感受野大小 = 3×3神经元 G 的感受野
┌─────────────┐
│ 0 1 2 3 4 5 6│
│ 1 [2][3][4]5 6 7│ 行1-3
│ 2 [3][4][5]6 7 8│
│ 3 [4][5][6]7 8 9│
│ 4 5 6 7 8 9 0│
│ 5 6 7 8 9 0 1│
│ 6 7 8 9 0 1 2│
└─────────────┘
列1-3
G = f(输入[1-3行, 1-3列])
感受野大小 = 3×3神经元 M 的感受野
┌─────────────┐
│ 0 1 2 3 4 5 6│
│ 1 2 3 4 5 6 7│
│ 2 3 [4][5][6]7 8│ 行2-4
│ 3 4 [5][6][7]8 9│
│ 4 5 [6][7][8]9 0│
│ 5 6 7 8 9 0 1│
│ 6 7 8 9 0 1 2│
└─────────────┘
列2-4
M = f(输入[2-4行, 2-4列])
感受野大小 = 3×33.4 第2层神经元 ε 的感受野(在第1层)
第2层神经元 ε 位于中心位置 [1,1]
它在第1层连接到3×3区域:
第1层特征图:
A B C D E
F [G H I] J
K [L M N] O ← ε 连接这9个神经元
P [Q R S] T
U V W X Y
ε = f(G, H, I, L, M, N, Q, R, S)
ε 在第1层的直接感受野 = {G, H, I, L, M, N, Q, R, S}3.5 将第2层的感受野映射回第0层(关键步骤!)
问题:ε 在原始输入(第0层)能"看到"多大的区域?
需要找出 G, H, I, L, M, N, Q, R, S 这9个第1层神经元各自在第0层的感受野,然后合并!
第1层各神经元在第0层的感受野
【G 在第0层的感受野】
┌─────────────┐
│ 0 1 2 3 4 5 6│
│ 1 [2][3][4]5 6 7│ 行1-3
│ 2 [3][4][5]6 7 8│
│ 3 [4][5][6]7 8 9│
│ 4 5 6 7 8 9 0│
└─────────────┘
列1-3【H 在第0层的感受野】
┌─────────────┐
│ 0 1 2 3 4 5 6│
│ 1 2 [3][4][5]6 7│ 行1-3
│ 2 3 [4][5][6]7 8│
│ 3 4 [5][6][7]8 9│
│ 4 5 6 7 8 9 0│
└─────────────┘
列2-4【I 在第0层的感受野】
┌─────────────┐
│ 0 1 2 3 4 5 6│
│ 1 2 3 [4][5][6]7│ 行1-3
│ 2 3 4 [5][6][7]8│
│ 3 4 5 [6][7][8]9│
│ 4 5 6 7 8 9 0│
└─────────────┘
列3-5【L 在第0层的感受野】
┌─────────────┐
│ 0 1 2 3 4 5 6│
│ 1 2 3 4 5 6 7│
│ 2 [3][4][5]6 7 8│ 行2-4
│ 3 [4][5][6]7 8 9│
│ 4 [5][6][7]8 9 0│
└─────────────┘
列1-3【M 在第0层的感受野】
┌─────────────┐
│ 0 1 2 3 4 5 6│
│ 1 2 3 4 5 6 7│
│ 2 3 [4][5][6]7 8│ 行2-4
│ 3 4 [5][6][7]8 9│
│ 4 5 [6][7][8]9 0│
└─────────────┘
列2-4【N 在第0层的感受野】
┌─────────────┐
│ 0 1 2 3 4 5 6│
│ 1 2 3 4 5 6 7│
│ 2 3 4 [5][6][7]8│ 行2-4
│ 3 4 5 [6][7][8]9│
│ 4 5 6 [7][8][9]0│
└─────────────┘
列3-5【Q 在第0层的感受野】
┌─────────────┐
│ 0 1 2 3 4 5 6│
│ 1 2 3 4 5 6 7│
│ 2 3 4 5 6 7 8│
│ 3 [4][5][6]7 8 9│ 行3-5
│ 4 [5][6][7]8 9 0│
└─────────────┘
列1-3【R 在第0层的感受野】
┌─────────────┐
│ 0 1 2 3 4 5 6│
│ 1 2 3 4 5 6 7│
│ 2 3 4 5 6 7 8│
│ 3 4 [5][6][7]8 9│ 行3-5
│ 4 5 [6][7][8]9 0│
└─────────────┘
列2-4【S 在第0层的感受野】
┌─────────────┐
│ 0 1 2 3 4 5 6│
│ 1 2 3 4 5 6 7│
│ 2 3 4 5 6 7 8│
│ 3 4 5 [6][7][8]9│ 行3-5
│ 4 5 6 [7][8][9]0│
└─────────────┘
列3-53.6 合并所有感受野
将G, H, I, L, M, N, Q, R, S这9个神经元覆盖的所有位置合并:
┌─────────────┐
│ 0 1 2 3 4 5 6│
│ 1 [2][3][4][5][6]7│ 行1
│ 2 [3][4][5][6][7]8│ 行2
│ 3 [4][5][6][7][8]9│ 行3
│ 4 [5][6][7][8][9]0│ 行4
│ 5 6 7 8 9 0 1│
│ 6 7 8 9 0 1 2│
└─────────────┘
列1 列2 列3 列4 列5
ε 在第0层的感受野:
- 行范围:1-5(共5行)
- 列范围:1-5(共5列)
- 感受野大小:5×5 ✓结论:两层3×3卷积后,第2层神经元的感受野是5×5!
四、感受野计算公式
4.1 递推公式
符号定义:
RF_l= 第 l 层的感受野大小k_l= 第 l 层的卷积核大小s_l= 第 l 层的步长
递推关系:
RF_{l+1} = RF_l + (k_{l+1} - 1) × ∏(i=1 to l) s_i
初始条件:
RF_0 = 1(输入层每个像素的感受野是它自己)4.2 简化公式(所有层stride=1)
当所有卷积层stride=1时:
RF_l = 1 + Σ(i=1 to l) (k_i - 1)
或者,如果所有卷积核大小相同(都是k):
RF_l = 1 + (k - 1) × l4.3 计算示例
示例1:两层3×3卷积,stride=1
第0层(输入):
RF_0 = 1
第1层(3×3卷积,stride=1):
RF_1 = RF_0 + (k_1 - 1) × s_0
= 1 + (3 - 1) × 1
= 1 + 2
= 3 ✓
第2层(3×3卷积,stride=1):
RF_2 = RF_1 + (k_2 - 1) × (s_0 × s_1)
= 3 + (3 - 1) × (1 × 1)
= 3 + 2
= 5 ✓
结论:第2层的感受野是 5×5示例2:三层3×3卷积,stride=1
RF_0 = 1
RF_1 = 1 + 2×1 = 3
RF_2 = 3 + 2×1 = 5
RF_3 = 5 + 2×1 = 7
结论:第3层的感受野是 7×7通用公式(所有层都是3×3,stride=1):
RF = 1 + 2×层数
1层 → RF = 3
2层 → RF = 5
3层 → RF = 7
4层 → RF = 9
5层 → RF = 11示例3:包含池化层
层级配置:
第1层:3×3卷积,stride=1
第2层:2×2池化,stride=2
第3层:3×3卷积,stride=1计算过程:
RF_0 = 1
RF_1 = 1 + (3-1)×1
= 3
RF_2 = 3 + (2-1)×1
= 4
↑ 池化核大小=2
RF_3 = 4 + (3-1)×(1×2)
↑累积步长 = s_1 × s_2 = 1×2
= 4 + 2×2
= 4 + 4
= 8
结论:第3层的感受野是 8×8关键点:池化层的stride会影响后续层的感受野增长速度!
示例4:VGG Block
配置:
Conv1: 3×3, stride=1
Conv2: 3×3, stride=1
MaxPool: 2×2, stride=2计算:
RF_0 = 1
RF_1 (Conv1) = 1 + 2×1 = 3
RF_2 (Conv2) = 3 + 2×1 = 5
RF_3 (MaxPool) = 5 + (2-1)×(1×1)
= 5 + 1
= 6
注意:虽然MaxPool的stride=2,但这里累积步长还是1×1
因为前面的卷积层stride都是1五、完整网络的感受野计算
5.1 ResNet第一个Block
层级结构:
输入 → Conv1(7×7, s=2) → MaxPool(3×3, s=2) → Conv2(3×3, s=1)逐层计算:
层0(输入):
RF_0 = 1
层1(7×7卷积,stride=2):
RF_1 = RF_0 + (k_1 - 1) × stride_0
= 1 + (7 - 1) × 1
= 1 + 6
= 7
层2(3×3池化,stride=2):
累积步长 = stride_1 = 2
RF_2 = RF_1 + (k_2 - 1) × stride_1
= 7 + (3 - 1) × 2
= 7 + 4
= 11
层3(3×3卷积,stride=1):
累积步长 = stride_1 × stride_2 = 2 × 2 = 4
RF_3 = RF_2 + (k_3 - 1) × (stride_1 × stride_2)
= 11 + (3 - 1) × 4
= 11 + 8
= 19
答案:第3层的感受野是 19×195.2 典型CNN的感受野演变
VGG-like 网络:
层级 感受野大小
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
输入 224×224×3 1×1
Conv1-1: 3×3, s=1 3×3
Conv1-2: 3×3, s=1 5×5
MaxPool: 2×2, s=2 6×6
Conv2-1: 3×3, s=1 10×10
Conv2-2: 3×3, s=1 14×14
MaxPool: 2×2, s=2 16×16
Conv3-1: 3×3, s=1 24×24
Conv3-2: 3×3, s=1 32×32
Conv3-3: 3×3, s=1 40×40
MaxPool: 2×2, s=2 44×44
观察:
- 越深的层,感受野越大
- 池化层使感受野"跳跃式"增长
- 深层神经元能看到更大的区域六、感受野的直觉理解
6.1 不同层"看到"的内容
【第1层:检测边缘】
感受野 3×3
原图: 神经元看到的:
███████████ [█ █] ← 只看到局部边缘
███████████ [█ █]
███████████
学习特征:横线、竖线、斜线、颜色变化
【第2层:检测纹理】
感受野 7×7
原图: 神经元看到的:
███████████ [█ █ █ █] ← 看到小块纹理
███████████ [█ █ █]
███████████ [█ █ █]
███████████ [█ █ █ █]
学习特征:网格、条纹、点状图案
【第5层:检测物体部件】
感受野 40×40
原图: 神经元看到的:
███████████ [整只眼睛] ← 看到完整部件
███████████ [ ●● ]
███████████ [ ● ● ]
███████████ [ ●● ]
学习特征:眼睛、轮子、门窗、耳朵
【第10层:检测完整物体】
感受野 >100×100
原图: 神经元看到的:
███████████ [整只猫] ← 看到大半个物体
███████████ [猫的头]
███████████ [和身体]
学习特征:猫、狗、汽车、房子6.2 为什么小卷积核更好?
方案对比:
【方案A:直接用大卷积核】
输入 → 7×7卷积 → 输出
感受野 = 7×7
参数量 = 7×7 = 49
非线性 = 1个ReLU
【方案B:堆叠小卷积核】
输入 → 3×3卷积 → 3×3卷积 → 3×3卷积 → 输出
RF=3 RF=5 RF=7
感受野 = 7×7(相同!)
参数量 = 3×3 + 3×3 + 3×3 = 27(少了45%!)
非线性 = 3个ReLU(更多!)
结论:
✓ 感受野相同
✓ 参数量更少
✓ 表达能力更强(更多非线性变换)
✓ 梯度流动更好
这就是为什么现代CNN都用3×3卷积!6.3 感受野与任务的关系
任务类型 所需感受野 网络深度
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
纹理分类 小(15×15) 浅(3-5层)
边缘检测 小(10×10) 浅(2-3层)
物体检测 大(100×100) 深(10-20层)
场景理解 很大(>200×200) 很深(50+层)
语义分割 全图 很深+特殊结构七、常见错误与纠正
错误1:简单相加卷积核大小
❌ 错误想法:
两层3×3卷积 → 感受野 = 3 + 3 = 6
✓ 正确计算:
RF = 1 + (k-1)×层数
= 1 + (3-1)×2
= 1 + 4
= 5错误2:忽略步长的累积效应
❌ 错误:
每层stride=2,两层后感受野增加 2+2=4
✓ 正确:
步长会累积相乘!
第1层增加:(k-1)×1
第2层增加:(k-1)×2
第3层增加:(k-1)×4
...错误3:混淆感受野和输出大小
【概念区分】
感受野(Receptive Field):
- 神经元在输入层能看到的区域大小
- 随着层数增加而增大
- 例:第5层感受野可能是 40×40
输出大小(Output Size):
- 特征图的空间维度
- 通常随着层数增加而减小
- 例:第5层输出可能只有 7×7
它们是完全不同的概念!错误4:单层感受野不等于卷积核
❌ 错误(针对非第一层):
第3层用3×3卷积,所以感受野是3×3
✓ 正确:
- 第1层:感受野 = 3×3(等于卷积核)
- 第2层:感受野 = 5×5(大于卷积核)
- 第3层:感受野 = 7×7(大于卷积核)
只有第一层的感受野等于卷积核大小!八 学习LeNet-5
8.1 LeNet 到底是什么
bash
经典的 LeNet-5 是一个小型 CNN,最早用来做手写数字识别(MNIST)。典型结构(用现代写法表达):
输入:1×32×32 灰度图(原版用 32×32;MNIST 是 28×28,所以我们要么 padding,要么直接适配)
C1:卷积 6@5×5 → 输出 6×28×28(如果输入 32×32)
S2:池化 2×2 → 输出 6×14×14
C3:卷积 16@5×5 → 输出 16×10×10
S4:池化 2×2 → 输出 16×5×5
C5:卷积 120@5×5 → 输出 120×1×1
F6:全连接 84
输出:全连接到类别数(MNIST=10)
现代 PyTorch 里我们通常用:
nn.Conv2d
nn.AvgPool2d(LeNet 原版是平均池化;现在也常用 MaxPool)
nn.ReLU(原版是 tanh/sigmoid,但 ReLU 训练更快更稳)
nn.Linear8.2 let-5 结构图
bash
### 2.1 LeNet-5 结构图输入: 32×32×1(灰度图像)
↓
┌─────────────────────────────────────┐
│ Conv1: 6个 5×5 卷积核 │
│ 输出: 28×28×6 │
│ 参数量: (5×5×1+1)×6 = 156 │
└─────────────────────────────────────┘
↓ ReLU激活
↓
┌─────────────────────────────────────┐
│ Pool1: 2×2 最大池化, stride=2 │
│ 输出: 14×14×6 │
│ 参数量: 0 │
└─────────────────────────────────────┘
↓
┌─────────────────────────────────────┐
│ Conv2: 16个 5×5 卷积核 │
│ 输出: 10×10×16 │
│ 参数量: (5×5×6+1)×16 = 2416 │
└─────────────────────────────────────┘
↓ ReLU激活
↓
┌─────────────────────────────────────┐
│ Pool2: 2×2 最大池化, stride=2 │
│ 输出: 5×5×16 │
│ 参数量: 0 │
└─────────────────────────────────────┘
↓ 展平 Flatten
↓ 5×5×16 = 400
┌─────────────────────────────────────┐
│ FC1: 全连接层 400 → 120 │
│ 参数量: 400×120 + 120 = 48,120 │
└─────────────────────────────────────┘
↓ ReLU激活
↓
┌─────────────────────────────────────┐
│ FC2: 全连接层 120 → 84 │
│ 参数量: 120×84 + 84 = 10,164 │
└─────────────────────────────────────┘
↓ ReLU激活
↓
┌─────────────────────────────────────┐
│ FC3: 全连接层 84 → 10(输出层) │
│ 参数量: 84×10 + 10 = 850 │
└─────────────────────────────────────┘
↓
输出: 10个类别的概率
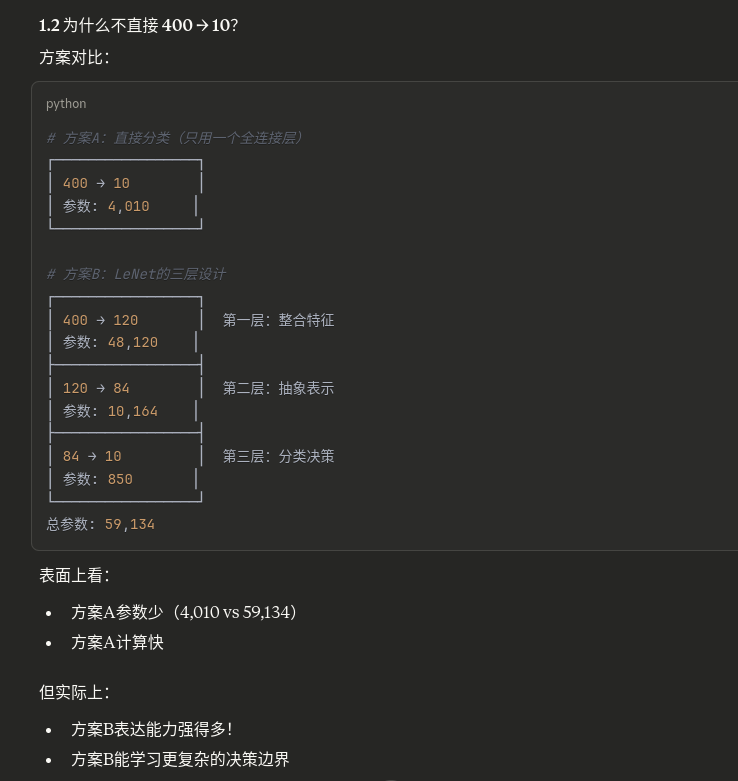
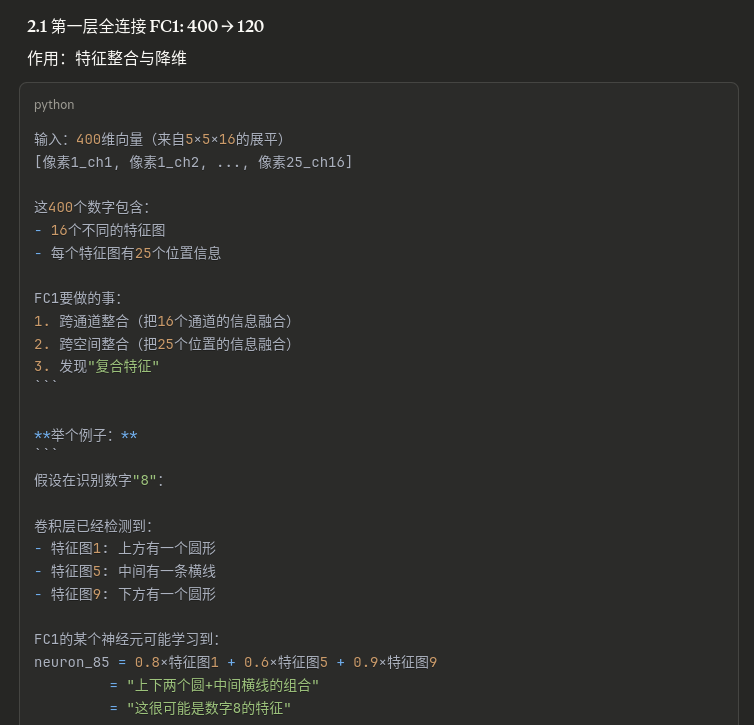
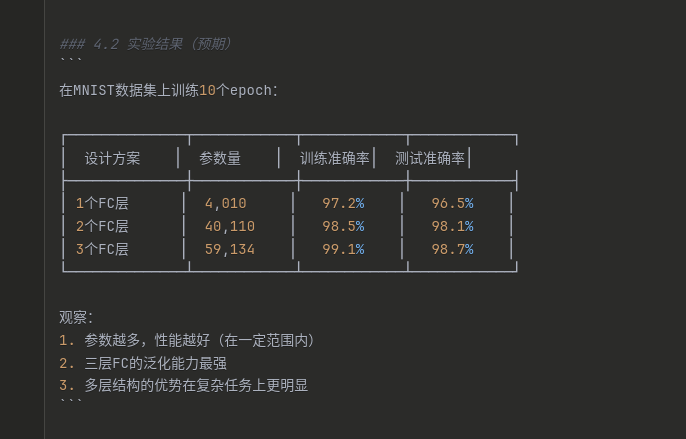
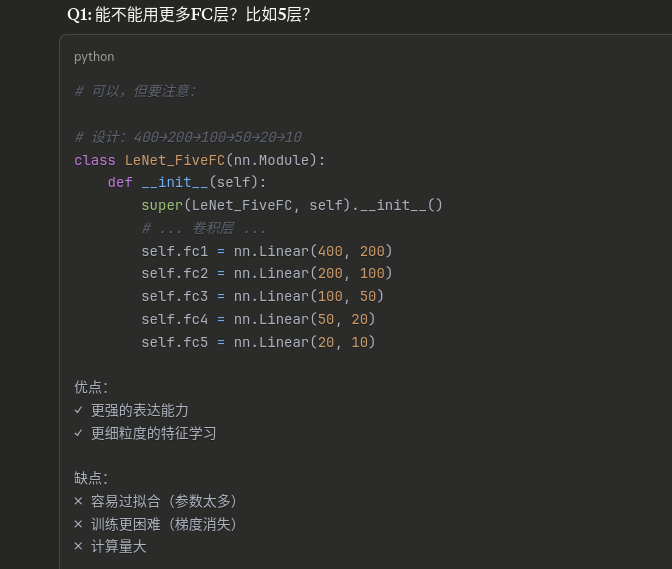
为什么最后执行三个全连接
九 GitHub Actions CI/入门指南简介
一、什么是 GitHub Actions?
GitHub Actions 是 GitHub 提供的 CI/CD(持续集成/持续部署)服务,可以自动化执行各种任务。

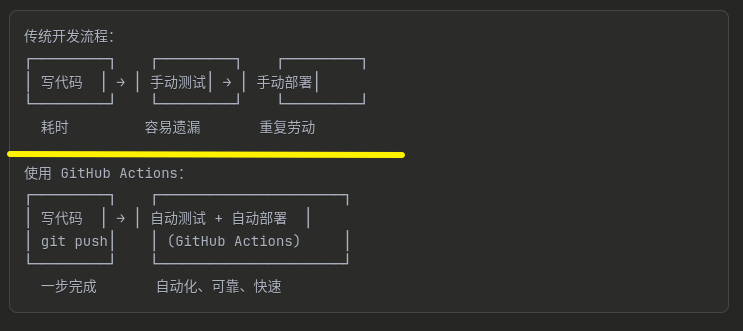
关键术语:

层级关系
Workflow (工作流)
└── Job 1 (任务1)
├── Step 1 (步骤1): Checkout 代码
├── Step 2 (步骤2): 安装 Python
├── Step 3 (步骤3): 安装依赖
└── Step 4 (步骤4): 运行测试
└── Job 2 (任务2)
└── ...
2.1 项目结构
创建一个标准的 Python 项目:
my-python-project/
├── .github/
│ └── workflows/ # GitHub Actions 配置文件目录
│ └── test.yml # 我们要创建的测试工作流
├── src/ # 源代码目录
│ ├── init .py
│ └── calculator.py # 示例代码
├── tests/ # 测试目录
│ ├── init .py
│ └── test_calculator.py # 测试文件
├── requirements.txt # 项目依赖
├── requirements-dev.txt # 开发依赖(包含pytest)
└── README.md
十C++ STL 容器完全指南:vector、map、set 深度学习

一、STL概述与容器分类
STL (Standard Template Library) 是C++标准库的核心部分。
STL 三大组件:
┌────────────────────────────────────────┐
│ 1. 容器 (Containers) │
│ - 存储数据的数据结构 │
│ - vector, map, set, list... │
├────────────────────────────────────────┤
│ 2. 算法 (Algorithms) │
│ - 操作容器的函数 │
│ - sort, find, count... │
├────────────────────────────────────────┤
│ 3. 迭代器 (Iterators) │
│ - 连接容器和算法的桥梁 │
│ - begin(), end(), ++, *... │
└────────────────────────────────────────┘
1.2 容器分类
STL 容器分类
├── 顺序容器 (Sequence Containers)
│ ├── vector 动态数组,连续内存
│ ├── deque 双端队列
│ ├── list 双向链表
│ ├── forward_list 单向链表
│ └── array 固定大小数组
│
├── 关联容器 (Associative Containers)
│ ├── 有序关联容器
│ │ ├── set 集合(唯一元素)
│ │ ├── multiset 集合(允许重复)
│ │ ├── map 键值对(唯一键)
│ │ └── multimap 键值对(允许重复键)
│ │
│ └── 无序关联容器 (C++11)
│ ├── unordered_set
│ ├── unordered_multiset
│ ├── unordered_map
│ └── unordered_multimap
│
└── 容器适配器 (Container Adapters)
├── stack 栈
├── queue 队列
└── priority_queue 优先队列
bash
// ============================================================
// 容器分类的底层原理
// ============================================================
/*
┌─────────────────────────────────────────────────────────┐
│ 容器分类及其内部实现 │
├─────────────────────────────────────────────────────────┤
│ │
│ 1. 顺序容器 (Sequence Containers) │
│ 特点:元素有序排列,位置由插入时间决定 │
│ │
│ vector ──────► 动态数组 │
│ │ 内存:连续 │
│ │ 增长策略:2倍或1.5倍 │
│ │ 迭代器:随机访问 │
│ │ │
│ deque ──────► 双端队列 │
│ │ 内存:分段连续(多个固定大小块) │
│ │ 中央控制器:维护块指针数组 │
│ │ 迭代器:随机访问 │
│ │ │
│ list ──────► 双向链表 │
│ │ 内存:非连续 │
│ │ 节点:prev, data, next │
│ │ 迭代器:双向 │
│ │ │
│ forward_list ──► 单向链表 │
│ │ 节点:data, next │
│ │ 迭代器:前向 │
│ │ │
│ array ──────► 固定大小数组 │
│ 编译期大小确定 │
│ 无内存开销 │
│ │
│ 2. 关联容器 (Associative Containers) │
│ 特点:元素按键自动排序 │
│ │
│ set/map ────► 红黑树 (Red-Black Tree) │
│ │ 平衡二叉搜索树 │
│ │ 性质: │
│ │ 1. 每个节点是红或黑 │
│ │ 2. 根节点是黑 │
│ │ 3. 叶节点(NIL)是黑 │
│ │ 4. 红节点的子节点是黑 │
│ │ 5. 从根到叶的黑节点数相同 │
│ │ │
│ │ 操作复杂度:O(log n) │
│ │ │
│ multiset/multimap │
│ 允许重复键的红黑树 │
│ │
│ 3. 无序关联容器 (Unordered Associative Containers) │
│ 特点:哈希表实现,无序 │
│ │
│ unordered_set/map ──► 哈希表 (Hash Table) │
│ 结构:桶数组 + 链表 │
│ 哈希函数:键 → 桶索引 │
│ 冲突解决:链地址法 │
│ 平均复杂度:O(1) │
│ 最坏复杂度:O(n) │
│ 负载因子:元素数/桶数 │
│ 自动rehash:超过阈值时扩容 │
│ │
└─────────────────────────────────────────────────────────┘
*/二、vector:动态数组
2.1 vector 基础概念
vector 的本质:
┌────────────────────────────────────┐
│ 动态数组 = 可变大小的数组 │
│ │
│ 内部结构: │
│ ┌──┬──┬──┬──┬──┬──┬──┬──┐ │
│ │0 │1 │2 │3 │4 │ │ │ │ ← 容量│
│ └──┴──┴──┴──┴──┴──┴──┴──┘ │
│ ↑ ↑ │
│ begin end │
│ 当前大小:5 │
│ 当前容量:8 │
└────────────────────────────────────┘
特点:
✓ 连续内存存储
✓ 随机访问 O(1)
✓ 尾部插入/删除 O(1)
✗ 中间插入/删除 O(n)
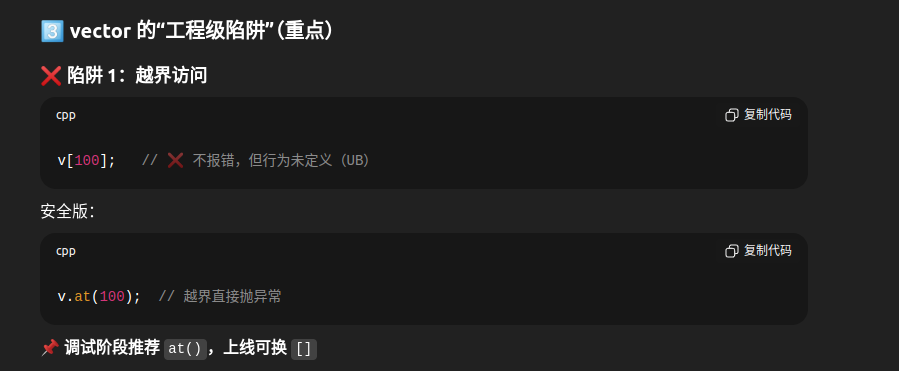

三、map:键值对容器
3.1 map 基础概念
bash
map 的本质:
┌────────────────────────────────────────┐
│ 键值对容器 = 关联数组 = 字典 │
│ │
│ 内部结构:红黑树(平衡二叉搜索树) │
│ │
│ ┌─────┐ │
│ │ "b" │ │
│ ╱ ╲ │
│ ╱ ╲ │
│┌───┐ ┌───┐ │
││"a"│ │"c"│ │
│└───┘ └───┘ │
│ ↓ ↓ │
│ 1 3 │
│ 2 │
│ │
│ {"a": 1, "b": 2, "c": 3} │
└────────────────────────────────────────┘
特点:
✓ 键唯一
✓ 自动排序(按键排序)
✓ 查找、插入、删除 O(log n)
✓ 不支持下标访问(除了用键访问)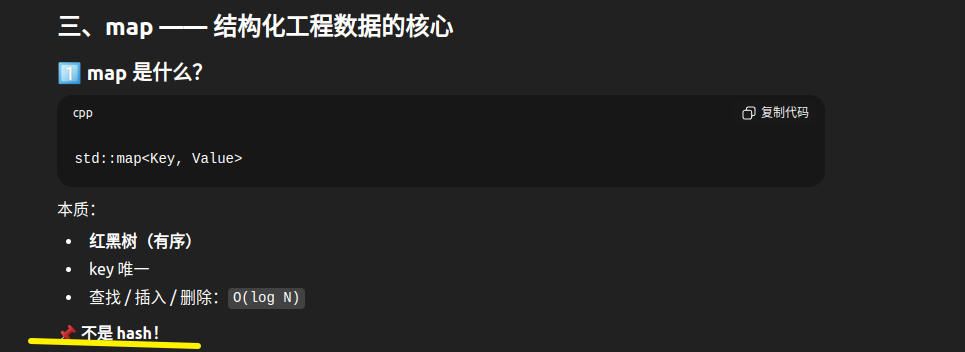
hash map 区别

四、set:集合容器
4.1 set 基础概念
bash
set 的本质:
┌────────────────────────────────────────┐
│ 集合 = 唯一元素的有序集合 │
│ │
│ 内部结构:红黑树(与map类似) │
│ │
│ ┌───┐ │
│ │ 5 │ │
│ ╱ ╲ │
│ ╱ ╲ │
│┌─┐ ┌─┐ │
││3│ │7│ │
│└─┘ └─┘ │
│ ╱╲ ╱╲ │
│1 4 6 9 │
│ │
│ {1, 3, 4, 5, 6, 7, 9} │
└────────────────────────────────────────┘
特点:
✓ 元素唯一(自动去重)
✓ 自动排序
✓ 查找、插入、删除 O(log n)
✓ 不能通过迭代器修改元素
六、性能分析与最佳实践
6.1 容器性能对比
bash
操作复杂度对比表:
┌─────────────┬────────┬────────┬────────┬────────┐
│ 操作 │ vector │ list │ map │ set │
├─────────────┼────────┼────────┼────────┼────────┤
│ 随机访问 │ O(1) │ O(n) │ N/A │ N/A │
│ 头部插入 │ O(n) │ O(1) │ N/A │ N/A │
│ 尾部插入 │ O(1)* │ O(1) │ N/A │ N/A │
│ 中间插入 │ O(n) │ O(1)** │log(n) │log(n) │
│ 查找 │ O(n) │ O(n) │log(n) │log(n) │
│ 删除 │ O(n) │ O(1)** │log(n) │log(n) │
└─────────────┴────────┴────────┴────────┴────────┘
* 摊销常数时间(可能触发重新分配)
** 假设已经有迭代器指向该位置
bash
// ============================================================
// 容器选择指南
// ============================================================
// 使用 vector 当:
// ✓ 需要随机访问
// ✓ 频繁在尾部插入/删除
// ✓ 内存连续性重要
// ✓ 大部分操作是读取
vector<int> v;
// 使用 list 当:
// ✓ 频繁在中间插入/删除
// ✓ 不需要随机访问
// ✓ 元素很大且移动代价高
list<LargeObject> l;
// 使用 deque 当:
// ✓ 需要在两端插入/删除
// ✓ 需要随机访问
// ✓ 不在乎内存是否连续
deque<int> d;
// 使用 map 当:
// ✓ 需要键值对存储
// ✓ 需要按键排序
// ✓ 频繁按键查找
map<string, int> m;
// 使用 unordered_map 当:
// ✓ 需要键值对存储
// ✓ 不需要排序
// ✓ 追求最快的查找速度
unordered_map<string, int> um;
// 使用 set 当:
// ✓ 需要唯一元素
// ✓ 需要自动排序
// ✓ 频繁判断元素存在性
set<int> s;
// 使用 unordered_set 当:
// ✓ 需要唯一元素
// ✓ 不需要排序
// ✓ 追求最快的查找速度
unordered_set<int> us;七、总结
7.1 核心知识点
bash
1. vector - 动态数组
├── 创建:vector<T> v; v.reserve(); v.resize()
├── 添加:push_back(), emplace_back(), insert()
├── 删除:pop_back(), erase(), clear()
├── 访问:[], at(), front(), back()
└── 容量:size(), capacity(), empty()
2. map - 键值对容器
├── 创建:map<K, V> m;
├── 插入:insert(), emplace(), []
├── 删除:erase(), clear()
├── 查找:find(), count(), at(), []
└── 遍历:范围for, 迭代器
3. set - 集合容器
├── 创建:set<T> s;
├── 插入:insert(), emplace()
├── 删除:erase(), clear()
├── 查找:find(), count()
└── 操作:并集、交集、差集7.2 最佳实践清单
✓ 预留空间 (reserve) 避免重新分配
✓ 使用 emplace 系列函数原地构造
✓ 传递容器时使用 const 引用
✓ 范围 for 循环使用 const 引用
✓ 选择合适的容器(根据操作特点)
✓ 避免不必要的拷贝
✓ 使用算法库(sort, find, count等)
✓ 注意迭代器失效问题
✓ map 查找时用 find 而非 []
✓ 删除元素时注意 erase-remove idiom十一CUDA 并行编程完全指南:线程索引与向量乘法
一、CUDA 编程模型基础
1.1 CPU vs GPU 架构
bash
CPU 架构:少量强大的核心
┌─────────────────────────────┐
│ Control │ Control │
│ ┌──────┐ │ ┌──────┐ │
│ │ ALU │ │ │ ALU │ │ 4-16 核心
│ │ ALU │ │ │ ALU │ │ 高频率 (3-5 GHz)
│ │ ALU │ │ │ ALU │ │ 大缓存
│ │ ALU │ │ │ ALU │ │ 复杂控制逻辑
│ └──────┘ │ └──────┘ │
│ Cache │ Cache │
└─────────────────────────────┘
核心1 核心2
GPU 架构:大量简单的核心
┌──────────────────────────────────────┐
│ ┌─┐┌─┐┌─┐┌─┐ ┌─┐┌─┐┌─┐┌─┐ │
│ │A││A││A││A│ │A││A││A││A│ │
│ └─┘└─┘└─┘└─┘ └─┘└─┘└─┘└─┘ │ 数千个核心
│ SM 1 SM 2 │ 中等频率 (1-2 GHz)
│ │ 小缓存
│ ┌─┐┌─┐┌─┐┌─┐ ┌─┐┌─┐┌─┐┌─┐ │ 简单控制逻辑
│ │A││A││A││A│ │A││A││A││A│ ... │
│ └─┘└─┘└─┘└─┘ └─┘└─┘└─┘└─┘ │
│ SM 3 SM 4 │
└──────────────────────────────────────┘
A = ALU (算术逻辑单元)
SM = Streaming Multiprocessor (流式多处理器)关键对比:
bash
CPU GPU
核心数 少 (4-16) 多 (数千)
频率 高 (3-5 GHz) 中 (1-2 GHz)
缓存 大 (MB级) 小 (KB级)
设计 复杂任务 大量简单任务
优势 串行性能 并行吞吐量1.2 CUDA 编程模型
bash
CUDA 编程模型:异构计算
CPU (Host) GPU (Device)
┌──────────┐ ┌─────────────────┐
│ 主程序 │ │ │
│ │ │ 并行 Kernel │
│ 数据 │ ──复制──→ │ │
│ 准备 │ │ thousands of │
│ │ │ threads │
│ 结果 │ ←──复制── │ │
│ 处理 │ │ │
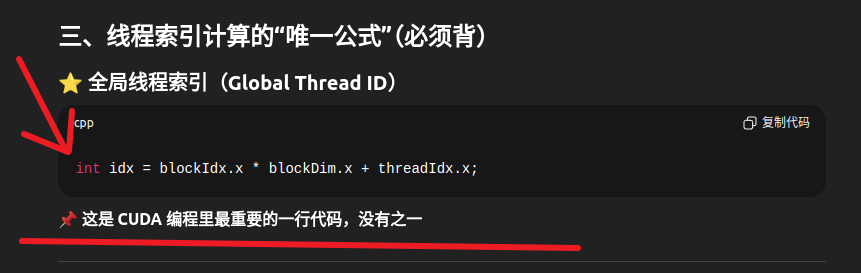
└──────────┘ └─────────────────┘ 线程索引计算的"唯一公式"(必须背
线程索引计算的"唯一公式"(必须背
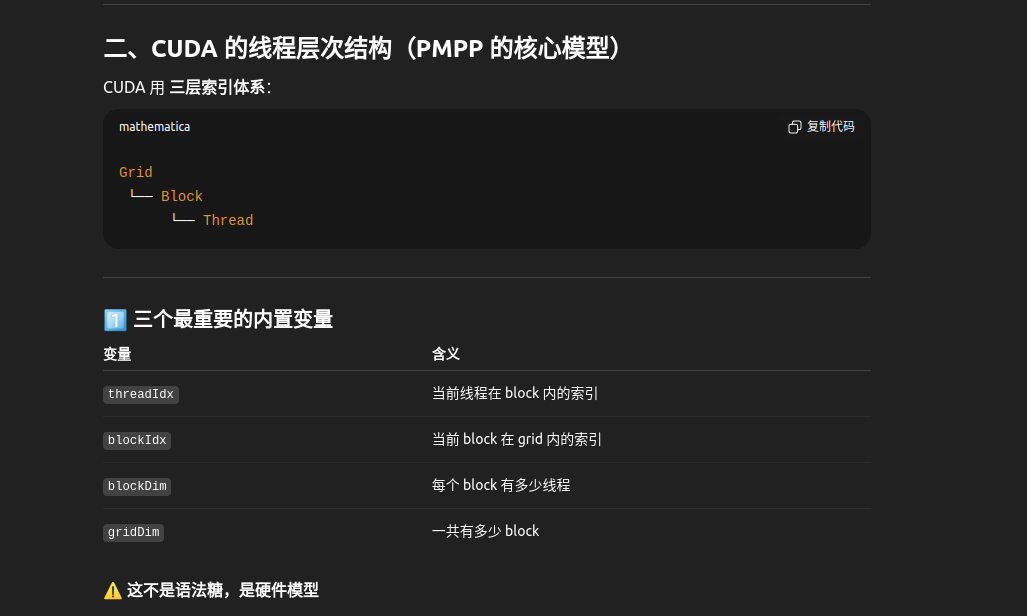
 2.2 内置变量详解
2.2 内置变量详解
bash
// ============================================================
// CUDA 内置变量
// ============================================================
// 在 Kernel 函数中可用的内置变量:
// 1. 线程索引(在 Block 内的位置)
threadIdx.x // 线程在 Block 中的 x 维度索引
threadIdx.y // 线程在 Block 中的 y 维度索引
threadIdx.z // 线程在 Block 中的 z 维度索引
// 2. Block 索引(在 Grid 内的位置)
blockIdx.x // Block 在 Grid 中的 x 维度索引
blockIdx.y // Block 在 Grid 中的 y 维度索引
blockIdx.z // Block 在 Grid 中的 z 维度索引
// 3. Block 维度(每个 Block 有多少线程)
blockDim.x // Block 在 x 维度的线程数
blockDim.y // Block 在 y 维度的线程数
blockDim.z // Block 在 z 维度的线程数
// 4. Grid 维度(Grid 有多少 Block)
gridDim.x // Grid 在 x 维度的 Block 数
gridDim.y // Grid 在 y 维度的 Block 数
gridDim.z // Grid 在 z 维度的 Block 数