效果一览
一、研究背景
- 任务类型:分类任务。
- 模型选择 :采用 Temporal Convolutional Network(TCN),相比传统RNN/LSTM,TCN具有更大的感受野、并行计算能力更强、梯度稳定等优势。
- 技术融合 :结合 贝叶斯优化(Bayesian Optimization) 进行自动超参数调优,以及 SHAP(SHapley Additive exPlanations) 进行模型解释,提升模型性能与可解释性。
二、主要功能
- 数据预处理:数据读取、类别分析、数据集划分、归一化、格式转换(转为TCN所需的cell格式)。
- 模型构建:构建可配置的TCN网络,支持残差块、卷积核数、丢弃率等参数调整。
- 超参数优化:使用贝叶斯优化自动搜索最优网络结构与训练参数。
- 模型训练与评估:训练优化后的TCN模型,进行预测并计算分类准确率。
- 可视化分析 :
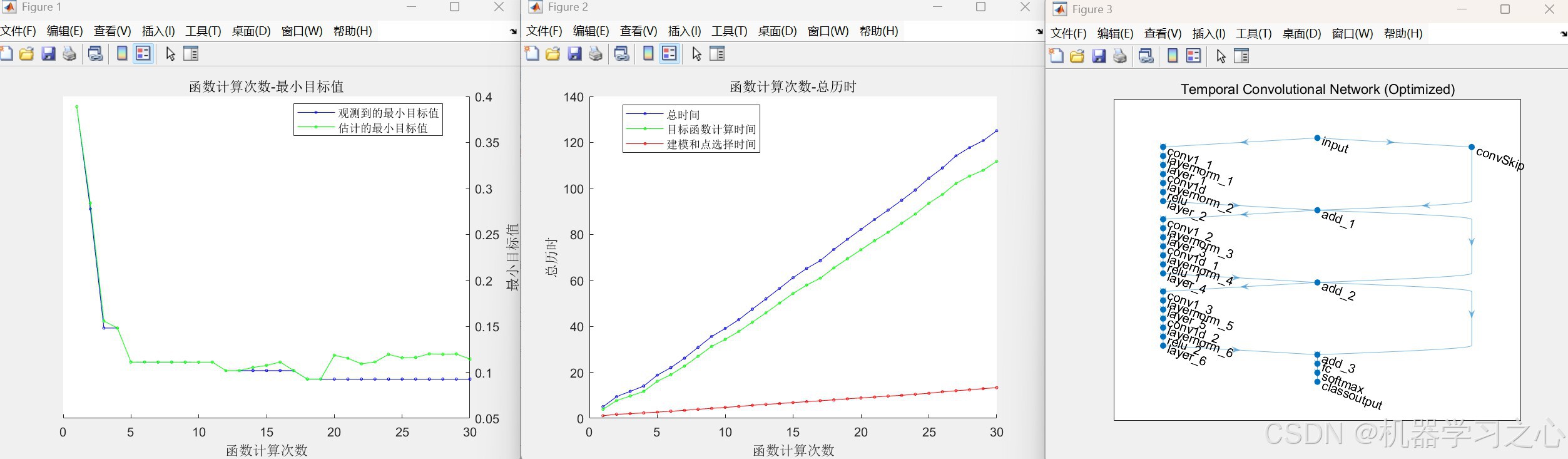
- 训练过程曲线
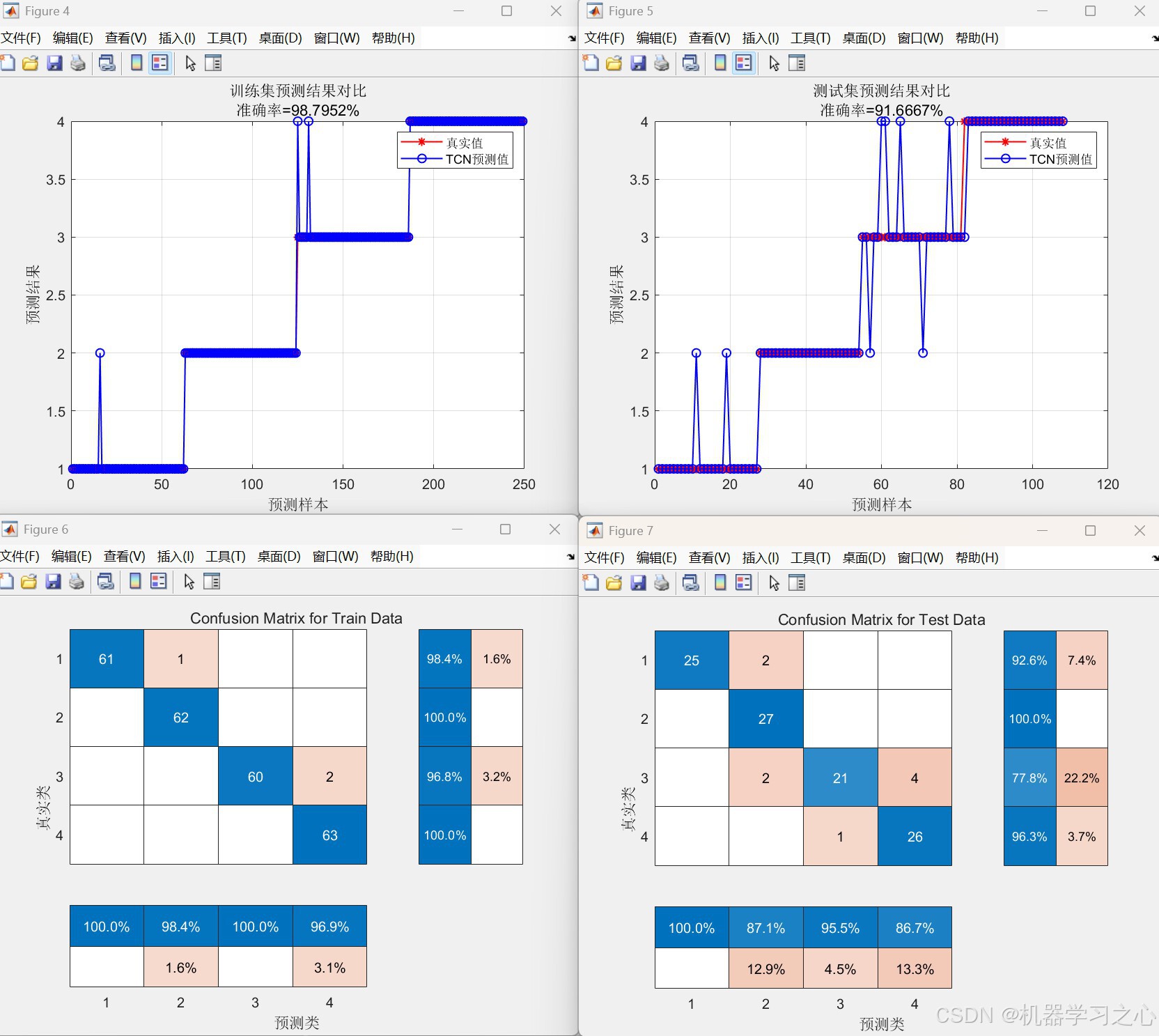
- 预测结果对比图
- 混淆矩阵
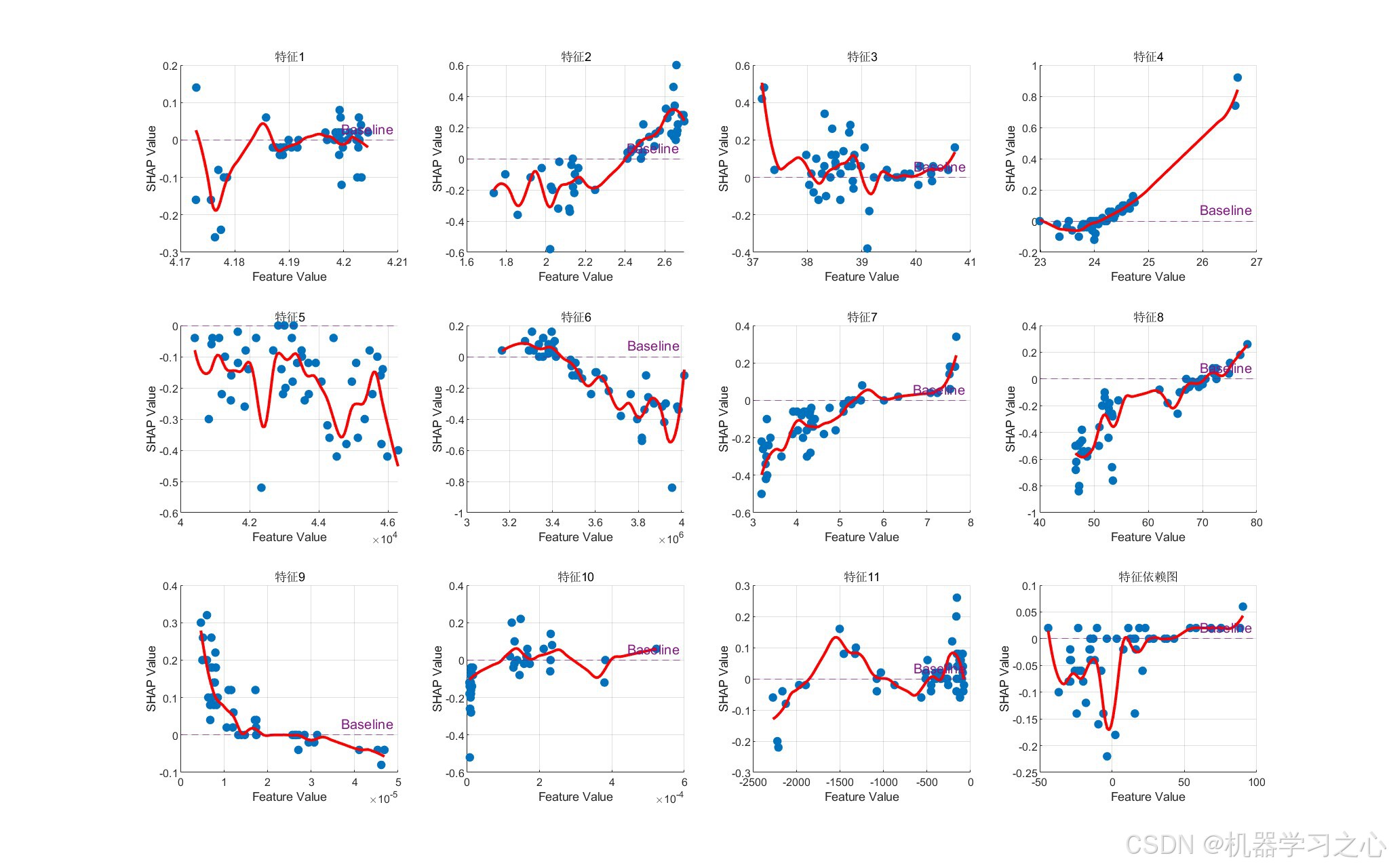
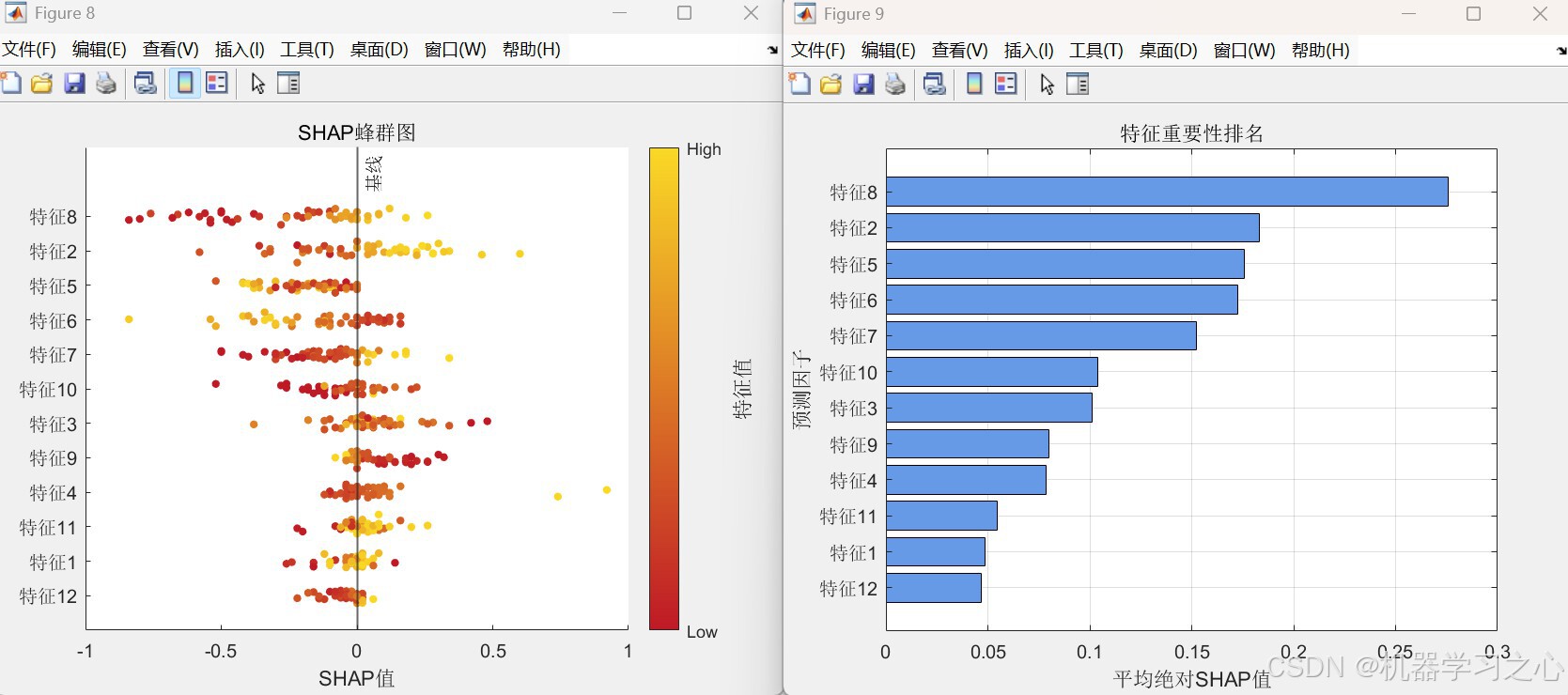
- SHAP特征重要性分析(摘要图、特征依赖图)
- 结果保存与报告:保存优化结果,输出最佳参数与性能指标。
三、算法步骤
- 数据准备:导入数据集,随机打乱,按类别划分训练集与测试集(70%-30%)。
- 数据归一化 :使用
mapminmax归一化至 [0,1]。 - 贝叶斯优化 :
- 定义超参数空间(卷积核数、大小、丢弃率、残差块数、学习率等)
- 使用贝叶斯优化迭代搜索最优参数组合
- 模型训练 :
- 使用优化后的超参数构建TCN网络
- 训练模型并监控训练过程
- 预测与评估 :
- 对训练集与测试集进行预测
- 计算分类准确率
- 绘制混淆矩阵
- SHAP分析 :
- 选择部分测试样本计算SHAP值
- 可视化特征重要性与依赖关系
- 结果输出:输出最佳参数、准确率、优化时间等信息。
四、技术路线
数据预处理 → 贝叶斯超参数优化 → TCN模型构建与训练 → 预测评估 → SHAP可解释性分析 → 结果可视化与保存五、核心公式/原理
- TCN :
- 使用扩张因果卷积(Dilated Causal Convolutions)
- 残差连接(Residual Connections)
- 公式:
yt=∑k=0K−1fk⋅xt−d⋅k y_t = \sum_{k=0}^{K-1} f_k \cdot x_{t-d \cdot k} yt=k=0∑K−1fk⋅xt−d⋅k
其中 (d) 为扩张因子,(K) 为卷积核大小。
- 贝叶斯优化 :
- 基于高斯过程回归(Gaussian Process Regression)建立目标函数模型
- 使用采集函数(如EI+)选择下一个评估点
- SHAP :
- 基于博弈论的Shapley值,计算特征对预测的贡献:
ϕi=∑S⊆N∖{i}∣S∣!(∣N∣−∣S∣−1)!∣N∣![f(S∪{i})−f(S)] \phi_i = \sum_{S \subseteq N \setminus \{i\}} \frac{|S|!(|N|-|S|-1)!}{|N|!} [f(S \cup \{i\}) - f(S)] ϕi=S⊆N∖{i}∑∣N∣!∣S∣!(∣N∣−∣S∣−1)![f(S∪{i})−f(S)]
- 基于博弈论的Shapley值,计算特征对预测的贡献:
六、参数设定
| 参数 | 说明 | 范围/取值 |
|---|---|---|
numFilters |
卷积核数量 | 8--32 |
filterSize |
卷积核大小 | 2--6 |
dropoutFactor |
丢弃率 | 0.05--0.3 |
numBlocks |
残差块数量 | 1--3 |
InitialLearnRate |
初始学习率 | 1e-4--1e-2 |
LearnRateDropFactor |
学习率下降因子 | 0.5--0.9 |
MaxEpochs(优化阶段) |
最大训练轮数 | 20 |
MaxEpochs(最终训练) |
最大训练轮数 | 120 |
LearnRateDropPeriod |
学习率下降周期 | 50 |
miniBatchSize |
批大小 | 30 |
七、运行环境
-
平台:MATLAB(建议R2020b及以上,支持混淆矩阵、贝叶斯优化等函数)
-
数据格式 :Excel文件(
.xlsx),最后一列为标签列
八、应用场景
- 分类问题:如医疗信号分类(ECG/EEG)、工业故障诊断等。
- 需解释性建模场景:如医疗诊断、金融风控等需要理解特征影响的领域。
- 自动化建模流程:适合需要快速调参、构建高性能分类模型的科研或工程应用。