从零手写RNN&BiRNN：从原理到双向实现

在学习深度学习框架时，调用API往往只是一行代码，但理解其内部计算原理才能真正掌握模型。本文将从头实现RNN（循环神经网络）的前向传播，包括单向和双向版本，并与PyTorch官方实现进行对比验证。

一、RNN基础原理

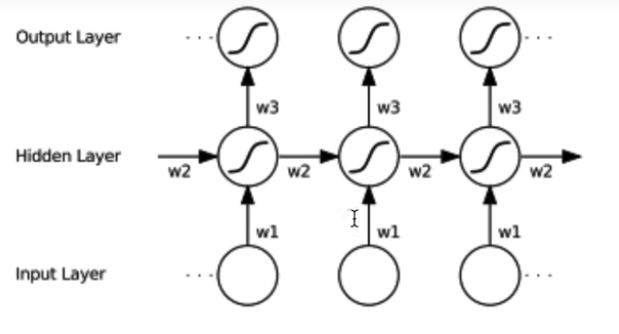
核心公式

RNN的计算公式如下：

h t = tanh ( W i h x t + b i h + W h h h ( t − 1 ) + b h h ) h_t = \text{tanh}(W_{ih}x_t + b_{ih} +W_{hh}h_{(t-1)}+ b_{hh}) ht=tanh(Wihxt+bih+Whhh(t−1)+bhh)

其中：

• h t h_t ht: 表示当前状态
• x t x_t xt: 表示当前时刻的输入
• W i h W_{ih} Wih: 表示RNN对当前输入 x t x_t xt的权重矩阵------从输入层到隐藏层的权重矩阵
• b i h b_{ih} bih: 表示RNN对当前输入 x t x_t xt的偏置
• h ( t − 1 ) h_{(t-1)} h(t−1): 表示RNN上一时刻的状态
• W h h W_{hh} Whh: 表示RNN对 h ( t − 1 ) h_{(t-1)} h(t−1)的权重矩阵------从隐藏层到隐藏层的权重矩阵（循环连接）
• b h h b_{hh} bhh: 表示RNN对 h ( t − 1 ) h_{(t-1)} h(t−1)的偏置

PyTorch RNN参数详解

参数：

• input_size -- 输入 x x x 中期望的特征数量（输入特征维度）
• hidden_size -- 隐藏状态 h h h 中的特征数量（隐藏层维度）
• num_layers -- 循环层的数量。例如，设置 num_layers=2 表示将两个RNN堆叠在一起形成堆叠RNN，其中第二个RNN接收第一个RNN的输出并计算最终结果。默认值：1
• nonlinearity -- 要使用的非线性激活函数。可以是 'tanh' 或 'relu'。默认值：'tanh'
• bias -- 如果为 False，则该层不使用偏置权重 b i h b_{ih} bih 和 b h h b_{hh} bhh。默认值：True
• batch_first -- 如果为 True，则输入和输出张量的格式为 (batch, seq, feature)（批次大小、序列长度、特征维度），而不是 (seq, batch, feature)。注意：这不适用于隐藏状态或细胞状态。详见下方输入/输出部分。默认值：False
• dropout -- 如果非零，则在除最后一层外的每个RNN层输出上引入 Dropout 层，dropout 概率等于该参数值。默认值：0
• bidirectional -- 如果为 True，则变为双向RNN。默认值：False，如果设置为True，则输出的大小是两倍的hidden_size

输入：input, hx

• input: 张量的形状为：

  • L L L is seq_len, N N N is batch size and H i n H_{in} Hin is input size.
  • 非批处理输入： ( L , H i n ) (L, H_{in}) (L,Hin)
  • batch_first=False 时： ( L , N , H i n ) (L, N, H_{in}) (L,N,Hin)，(seq, batch, feature)
  • batch_first=True 时： ( N , L , H i n ) (N, L, H_{in}) (N,L,Hin)，(batch, seq, feature)

  包含输入序列的特征。输入也可以是打包的变长序列（packed variable length sequence）。

• hx: 张量的形状为：

  • 非批处理输入： ( D × num_layers , H o u t ) (D \times \text{num\layers}, H{out}) (D×num_layers,Hout)
  • 批处理输入： ( D × num_layers , N , H o u t ) (D \times \text{num\layers}, N, H{out}) (D×num_layers,N,Hout)

  包含输入序列批次的初始隐藏状态。如果未提供，默认为零。

其中：

N = batch size（批次大小） L = sequence length（序列长度） D = 2 如果 bidirectional=True，否则为 1 H i n = input_size（输入维度） H o u t = hidden_size（隐藏层维度） \begin{aligned} N &= \text{batch size（批次大小）} \\ L &= \text{sequence length（序列长度）} \\ D &= 2 \text{ 如果 bidirectional=True，否则为 } 1 \\ H_{in} &= \text{input\size（输入维度）} \\ H{out} &= \text{hidden\_size（隐藏层维度）} \end{aligned} NLDHinHout=batch size（批次大小）=sequence length（序列长度）=2 如果 bidirectional=True，否则为 1=input_size（输入维度）=hidden_size（隐藏层维度）

输出：output, h_n

• output: 张量的形状为：

  • 非批处理输入： ( L , D × H o u t ) (L, D \times H_{out}) (L,D×Hout)
  • batch_first=False 时： ( L , N , D × H o u t ) (L, N, D \times H_{out}) (L,N,D×Hout)
  • batch_first=True 时： ( N , L , D × H o u t ) (N, L, D \times H_{out}) (N,L,D×Hout)

  包含RNN最后一层在每个时刻 t t t 的输出特征 ( h t ) (h_t) (ht)。

• h_n: 张量的形状为：

  • 非批处理输入： ( D × num_layers , H o u t ) (D \times \text{num\layers}, H{out}) (D×num_layers,Hout)
  • 批处理输入： ( D × num_layers , N , H o u t ) (D \times \text{num\layers}, N, H{out}) (D×num_layers,N,Hout)

  包含批次中每个元素的最终隐藏状态。

二、手撕单向RNN

首先准备数据，并调用PyTorch官方API作为对比基准：

import torch
import torch.nn as nn

batch_size, sequence_len = 2, 3
input_size, hidden_size = 2, 3 #输入层大小即(num_features), 隐藏层大小

input = torch.randn(batch_size, sequence_len, input_size) # 随机初始化一个输入特征序列 input: [B, L, Hin(input_size)]
h_prev = torch.zeros(batch_size, hidden_size) # 初始化隐含状态 h_prev: [B, hidden_size]

# step1 调用PyTorch RNN API
rnn = nn.RNN(input_size=input_size, hidden_size=hidden_size, batch_first=True)

# rnn_output: [B, L, D*Hout] state_final: [D*numlayers, B, Hout]
rnn_output, state_final = rnn(input, h_prev.unsqueeze(0)) 

接下来是核心部分------手动实现RNN前向传播：

# step2 手写一个rnn_forward(), 实现单向RNN的计算原理
def rnn_forward(input, weight_ih, weight_hh, bias_ih, bias_hh, h_prev):

    # weight_ih: [Hout, Hin] 即 [h_dim, Hin]
    # weight_hh: [Hout, Hout]
    batch_size, sequence_len, input_size = input.shape
    
    h_dim = weight_ih.shape[0] # h_dim is hidden_size   weight_ih:[Hout, Hin] 
    h_out = torch.zeros(batch_size, sequence_len, h_dim) # [B, L, Hout] 初始化一个输出状态矩阵

    for t in range(sequence_len):
        # input: [B, L, Hin]
        # 获取当前时刻输入特征
        x = input[: , t, :] # 获取在所有batch下, 第t时刻下, 全部的input
        # 所以x: [B, Hin]
        x = x.unsqueeze(2)
        # x.unsqueeze(2): [B, Hin, 1]
        # weight_ih: [Hout, Hin]
        # weight_ih_batch: [1, Hout, Hin]--->[B, Hout, Hin]
        # weight_hh_batch: [1, Hout, Hout]--->[B, Hout, Hout]
        weight_ih_batch = weight_ih.unsqueeze(0).tile(batch_size, 1, 1) # [B, Hout, Hin]
        weight_hh_batch = weight_hh.unsqueeze(0).tile(batch_size, 1, 1) # [B, Hout, Hout]

        # torch.bmm() Batch Matrix Multiplication（批次矩阵乘法）,用于对多个矩阵对同时进行矩阵乘法
        # 可以用torch.matmul()代替
        # weight_ih_batch: [B, Hout, Hin]
        # x: [B, Hin, 1]
        w_times_x = torch.bmm(weight_ih_batch, x) # w_times_x: [B, Hout, 1]
        w_times_x = w_times_x.squeeze(-1) # w_times_x: [B, Hout]

        # h_prev: [B, Hout]
        # weight_hh: [B, Hout, Hout]
        # h_prev.unsqueeze(2): [B, Hout, 1]
        w_times_h = torch.bmm(weight_hh_batch, h_prev.unsqueeze(2)) # w_times_h: [B, Hout, 1]
        w_times_h = w_times_h.squeeze(-1) # w_times_h: [B, Hout]

        h_prev = torch.tanh(w_times_x + bias_ih + w_times_h + bias_hh) # h_prev: [B, Hout]
        
        # 将当前时间步的隐藏状态 h_prev 存入 h_out 的第 t 个位置。
        # h_prev: [B, Hout]
        # h_out[:, t, :]: [B, Hout]
        # h_out: [B, L, Hout]
        h_out[:, t, :] = h_prev
    
    h_prev = h_prev.unsqueeze(0) # h_prev:[B, Hout]--->[1, B, Hout]
    return h_out, h_prev # h_out: [B, L, Hout]  h_prev: [1, B, Hout]

关键实现细节解析：

1. 批次矩阵乘法（bmm） ：为了实现批次并行计算，需要将权重矩阵扩展到批次维度。weight_ih.unsqueeze(0).tile(batch_size, 1, 1) 将 [Hout, Hin] 扩展为 [B, Hout, Hin]，使得每个样本都能应用相同的权重进行并行计算。

2. 维度对齐 ：输入 x 的形状是 [B, Hin]，通过 unsqueeze(2) 变为 [B, Hin, 1]，这样与 [B, Hout, Hin] 进行 bmm 后得到 [B, Hout, 1]，再 squeeze 回 [B, Hout]。

3. 状态存储 ：h_out 用于存储所有时间步的输出（对应PyTorch的 output），而 h_prev 在循环结束后保存最后时刻的状态（对应PyTorch的 h_n）。

验证实现正确性：

# 验证单向RNN的准确性
# k是参数, v是name, 获取前面调用RNN 的API的参数, 以该参数输入我们手搓的单向RNN, 如果结果与RNN API的输出结果一致, 说明成功

custom_rnn_output, custom_state_final = rnn_forward(
        input, rnn.weight_ih_l0, rnn.weight_hh_l0,
        rnn.bias_ih_l0, rnn.bias_hh_l0, h_prev
)

print("Pytorch API output:")
print(rnn_output, state_final)
print("rnn_forward function output:")
print(custom_rnn_output, custom_state_final)

如果两者输出一致，说明我们的手写实现与PyTorch内部计算逻辑完全吻合。

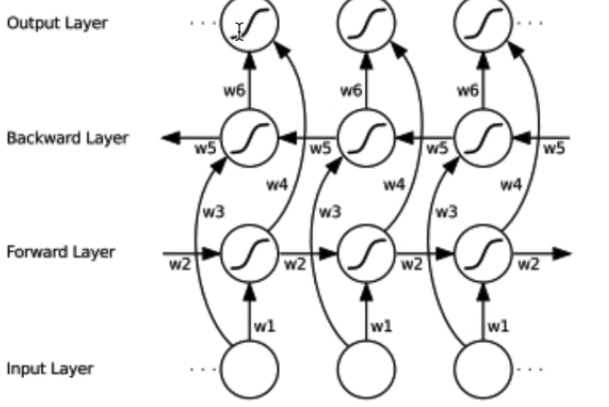
三、手撕双向RNN（Bi-RNN）

双向RNN包含两个独立的RNN：一个按正序处理序列（Forward），一个按逆序处理序列（Backward）。最终输出是两者拼接。

# step3 手写一个bidirectional_rnn_forward(), 实现双向RNN的计算原理
def bidirectional_rnn_forward(
    input, weight_ih, weight_hh, bias_ih, bias_hh, h_prev,
    weight_ih_reverse, weight_hh_reverse, bias_ih_reverse, bias_hh_reverse, h_prev_reverse,
):
    # weight_ih: [Hout, Hin] 即 [h_dim, Hin]
    # weight_hh: [Hout, Hout]
    batch_size, sequence_len, input_size = input.shape
    
    h_dim = weight_ih.shape[0] # h_dim is hidden_size   weight_ih:[Hout, Hin] 
    h_out = torch.zeros(batch_size, sequence_len, h_dim*2) # [B, L, Hout*D] 初始化一个输出状态矩阵, 双向是两倍的特征大小

    # forward layer
    forward_output = rnn_forward(input, weight_ih, weight_hh, bias_ih, bias_hh, h_prev)[0] # 只获取`output`

    # backward layer
    # torch.flip(input, dims)：沿指定维度翻转张量，dims 是要翻转的维度列表。
    # 需要翻转sequence_len
    backward_output = rnn_forward(
                        torch.flip(input, [1]), weight_ih_reverse, weight_hh_reverse,
                        bias_ih_reverse, bias_hh_reverse, h_prev_reverse
                       )[0] # 只获取`output`
    
    # 把forward_output 和 backward_output填充到h_out中
    h_out[:, :,:h_dim] = forward_output
    h_out[:, :, h_dim: ] = torch.flip(backward_output, [1])

    # 获取最后一个维度的状态
    h_n = torch.zeros(batch_size, 2, h_dim) # h_n: [B, 2, Hout]
    h_n[:, 0, :] = forward_output[:, -1, :] # 最后时刻的状态在L=0时候, 拼接上forward_output倒数第一个时刻的全部Hout
    h_n[:, 1, :] = backward_output[:, -1, :] # 最后时刻的状态在L=1时候, 拼接上backward_output倒数第一个时刻的全部Hout
  
    h_n = h_n.transpose(0, 1) # h_n: [2, B, Hout]
    
    # h_out: [B, L, Hout*2]
    # h_n: [2 , B, Hout]
    return h_out, h_n

双向RNN的实现要点：

1. 反向处理 ：使用 torch.flip(input, [1]) 将序列沿时间维度翻转，这样原来的最后一个时间步变成了第一个，实现了反向传播。

2. 输出拼接 ：h_out 的形状是 [B, L, Hout*2]，前 Hout 维存储正向结果，后 Hout 维存储反向结果。注意反向输出需要再次 flip 回来，保证时间步对齐。

3. 最终状态处理 ：h_n 需要包含两个方向的最后状态。注意对于反向层，虽然我们在翻转后的序列上计算，但 backward_output[:, -1, :] 实际上对应原序列的第一个时间步的状态（因为翻转了）。

验证双向RNN：

# 验证一下bidirectional_rnn_forward的正确性
bi_rnn = nn.RNN(input_size=input_size, hidden_size=hidden_size, batch_first=True, bidirectional=True)
h_prev = torch.zeros(2, batch_size, hidden_size)
bi_rnn_output, bi_state_final = bi_rnn(input, h_prev)

custom_bi_rnn_output, custom_bi_state_final = bidirectional_rnn_forward(
    input, bi_rnn.weight_ih_l0, bi_rnn.weight_hh_l0,
    bi_rnn.bias_ih_l0, bi_rnn.bias_hh_l0, h_prev[0],
    bi_rnn.weight_ih_l0_reverse, bi_rnn.weight_hh_l0_reverse,
    bi_rnn.bias_ih_l0_reverse,
    bi_rnn.bias_hh_l0_reverse, h_prev[1],
)

print("Pytorch API output:")
print(bi_rnn_output, bi_state_final)
print("custom bi_rnn_forward function output:")
print(custom_bi_rnn_output, custom_bi_state_final)

四、RNN的优缺点总结

• RNN的优点:

  • 可处理变长序列
  • 模型大小与序列长度无关
  • 计算量与序列长度呈线性增长
  • 考虑历史信息
  • 便于流式输出
  • 权重时不变

• RNN的缺点:

  • 串行计算比较慢
  • 无法获取太长的历史信息（梯度消失/爆炸问题）

五、总结

通过手撕RNN的实现，我们深入理解了：

1. 循环机制：隐藏状态如何在时间步之间传递
2. 批次处理 ：如何使用 bmm 实现高效的并行计算
3. 双向结构：如何通过翻转序列实现双向信息融合
4. 维度对齐 ：理解PyTorch中各种 [B, L, H]、[L, B, H] 等格式转换

虽然实际项目中我们直接使用 nn.RNN 即可，但这种底层实现训练有助于理解更复杂的变体（如LSTM、GRU）以及进行自定义修改（如加入注意力机制等）。

---

完整代码已验证：上述代码可直接运行，输出结果与PyTorch官方API完全一致，证明我们的数学推导和实现逻辑正确无误。