系列文章目录
- 【3DV 进阶-4】VecSet 论文+代码对照理解
- 【3DV 进阶-5】3D生成中 Inductive Bias (归纳偏置)的技术路线图
- 【3DV 进阶-6】为什么3D点云是无序集合?而2D图片是有序的呢?
- 【3DV 进阶-7】Hunyuan3D2.1-ShapeVAE 整体流程
- 【3DV 进阶-10】Trellis 中的表示 SLat 理解
- 【3DV 进阶-11】Trellis.2 数据处理与训练流程图
- 【3DV 进阶-12】Trellis.2 数据处理脚本细节
- 【3D-AICG 系列-1】Trellis v1 和 Trellis v2 的区别和改进
文章目录
- 系列文章目录
- [Flexible Dual Grid:Mesh ↔ O-Voxel 双向转换详解](#Flexible Dual Grid:Mesh ↔ O-Voxel 双向转换详解)
-
- 概述
- [Part 1: Mesh → O-Voxel(编码)](#Part 1: Mesh → O-Voxel(编码))
-
- 整体流程
- [Step 1: 构建原始网格与对偶网格](#Step 1: 构建原始网格与对偶网格)
- [Step 2: 收集 Hermite 数据](#Step 2: 收集 Hermite 数据)
- [Step 3: 最小化 QEF 求解对偶顶点](#Step 3: 最小化 QEF 求解对偶顶点)
- [Part 2: O-Voxel → Mesh(解码)](#Part 2: O-Voxel → Mesh(解码))
-
- 整体流程
- [Step 1: 找到活跃边和对偶顶点](#Step 1: 找到活跃边和对偶顶点)
- [Step 2: 连接四边形](#Step 2: 连接四边形)
- [Step 3: 灵活分割为三角形](#Step 3: 灵活分割为三角形)
- 完整数据流
- 核心优势
- 代码索引
由于 Trellis 2 中的 O-voxel 分为 Shape 和 Material 两个部分,本文先聚焦于 Shape: Flexible Dual Grid 这部分。
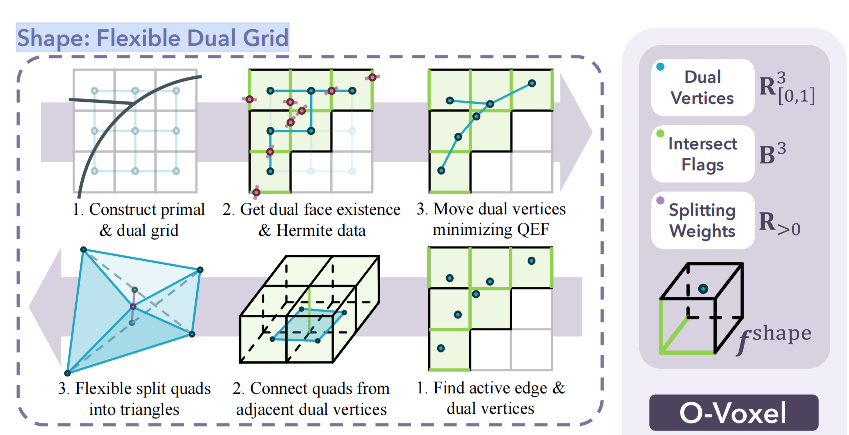

Flexible Dual Grid:Mesh ↔ O-Voxel 双向转换详解
基于 TRELLIS 2 源码的算法解析
概述
Flexible Dual Grid 实现了 Mesh 和 O-Voxel 之间的高效双向转换:
┌────────────┐ ┌────────────┐
│ │ ═══► 编码 (Encode) ═══► │ │
│ Mesh │ │ O-Voxel │
│ (三角面片) │ ◄═══ 解码 (Decode) ◄═══ │ (稀疏体素) │
└────────────┘ └────────────┘Part 1: Mesh → O-Voxel(编码)
整体流程
┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐
│ 1. 构建网格 │ │ 2. 收集数据 │ │ 3. 优化位置 │
│ Construct │ ─► │ Get Hermite │ ─► │ Minimize │
│ Grid │ │ Data │ │ QEF │
└─────────────────┘ └─────────────────┘ └─────────────────┘Step 1: 构建原始网格与对偶网格
目标:找出所有被 Mesh 表面穿过的体素
算法:扫描线填充(从 X/Y/Z 三个方向)
cpp
// flexible_dual_grid.cpp: intersect_qef() 第 96-170 行
auto scan_line_fill = [&](const int ax2) {
// 对每个三角形,从 ax2 方向扫描
// 找出所有与网格边相交的体素
for (int y_idx = start; y_idx < end; ++y_idx) {
for (int x_idx = line_start; x_idx < line_end; ++x_idx) {
// 计算交点 z 坐标
double z = lerp(...);
// 标记 4 个相邻体素
for (dx, dy in {0,1} × {0,1}) {
hash_table[coord] = voxels.size();
voxels.push_back(coord);
}
}
}
};
scan_line_fill(0); // 从 X 方向
scan_line_fill(1); // 从 Y 方向
scan_line_fill(2); // 从 Z 方向输出:
voxels[]- 所有被占据的体素坐标hash_table- 坐标 → 索引的映射
Step 2: 收集 Hermite 数据
Hermite 数据包含:
- 边相交标记
intersected[i]- 体素的哪条边与表面相交 - 交点均值
means[i]- 所有交点的平均位置 - QEF 矩阵
qefs[i]- 用于后续优化的误差函数
cpp
// 三种 QEF 来源:
// 1. 边相交 QEF(主要)
intersect_qef(...); // 第 61-172 行
// Q = plane × planeᵀ,其中 plane = [n, -n·v₀]
// 2. 面 QEF(补充贴合度)
face_qef(...); // 第 175-288 行
// 对与三角形相交的体素累加 Q
// 3. 边界 QEF(处理开放网格)
boundry_qef(...); // 第 291-383 行
// 只被 1 个三角形使用的边 = 边界边
// Q = I - d·dᵀ(到直线距离)边界边检测:
cpp
// 第 530-537 行
std::map<pair<int,int>, int> edge_count;
for (每个三角形的 3 条边) {
edge_count[{v0, v1}]++;
}
// edge_count == 1 → 边界边Step 3: 最小化 QEF 求解对偶顶点
目标:找到体素内最优的对偶顶点位置
数学形式:
minimize E(v) = vᵀ Q v
subject to v ∈ [voxel_min, voxel_max]求解策略(第 561-765 行):
cpp
// 1. 尝试无约束解
Eigen::Vector3f v = A.solve(b); // A = Q[0:3,0:3], b = -Q[0:3,3]
if (v 在体素内) {
return v; // 直接使用
}
// 2. 约束求解(解在体素外时)
float best_error = ∞;
// 2.1 面约束(固定 1 个坐标)→ 6 种情况
for (axis in {x,y,z}, bound in {min,max}) {
solve_2D_on_face();
}
// 2.2 边约束(固定 2 个坐标)→ 12 种情况
for (free_axis in {x,y,z}, 4种边界组合) {
solve_1D_on_edge();
}
// 2.3 角约束(固定 3 个坐标)→ 8 个角点
for (8 corners) {
evaluate_error();
}
return argmin(best_error);直观理解:
无约束解在外部时:
┌─────────┐
│ │ × 无约束解
│ │ ↗
│ │ /
│ •────┼───/── 约束后的解(在面上)
└─────────┘Part 2: O-Voxel → Mesh(解码)
整体流程
┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐
│ 1. 找活跃边 │ │ 2. 连接四边形 │ │ 3. 分割三角形 │
│ Find Active │ ─► │ Connect │ ─► │ Split │
│ Edges │ │ Quads │ │ Triangles │
└─────────────────┘ └─────────────────┘ └─────────────────┘Step 1: 找到活跃边和对偶顶点
活跃边 :被表面穿过的体素边,由 intersected[] 标记
cpp
// flexible_dual_grid.cpp: face_from_dual_vertices() 第 425-427 行
for (int i = 0; i < dual_vertices.size(); ++i) {
int3 coord = voxels[i];
bool3 is_intersected = intersected[i];
// is_intersected = {x边活跃?, y边活跃?, z边活跃?}
}图示:
z
│
│ • 对偶顶点
────┼────────
/│╲
/ │ ╲ ← 活跃边(intersected[2]=true 表示 z 方向边活跃)
/ │ ╲Step 2: 连接四边形
原理:每条活跃边连接 4 个相邻体素的对偶顶点,形成一个四边形
cpp
// 第 429-456 行
// 查找 6 个可能的邻居
size_t neigh[6] = {
hash[{x+1, y, z }], // 0: +x
hash[{x, y+1, z }], // 1: +y
hash[{x+1, y+1, z }], // 2: +x+y
hash[{x, y, z+1}], // 3: +z
hash[{x+1, y, z+1}], // 4: +x+z
hash[{x, y+1, z+1}], // 5: +y+z
};
// z 轴边活跃 → 连接 xy 平面的 4 个体素
if (intersected[2] && neigh[0,1,2] 都存在) {
quad = {i, neigh[0], neigh[2], neigh[1]};
}图示:
neigh[1]─────neigh[2]
│ ╲ ╱ │
│ ╲ ╱ │
│ ╳ │ ← 四边形(由 4 个对偶顶点组成)
│ ╱ ╲ │
│ ╱ ╲ │
i ─────────neigh[0]
↑
活跃的 z 边Step 3: 灵活分割为三角形
问题:四边形有两种分割方式,哪种更好?
方案 A (对角线 AC) 方案 B (对角线 BD)
A───B A───B
│╲ │ │ ╱│
│ ╲ │ │ ╱ │
│ ╲│ │╱ │
D───C D───C决策标准:选择两个三角形法向量更对齐的分割
cpp
// quad_to_2tri() 第 386-415 行
// 计算两种分割的法向量夹角
Eigen::Vector3f n_ABC = (B-A).cross(C-A).normalized();
Eigen::Vector3f n_ACD = (C-A).cross(D-A).normalized();
float angle_AC = acos(n_ABC.dot(n_ACD));
Eigen::Vector3f n_ABD = (B-A).cross(D-A).normalized();
Eigen::Vector3f n_BCD = (C-B).cross(D-B).normalized();
float angle_BD = acos(n_ABD.dot(n_BCD));
// 选择夹角更小的(更平滑)
if (angle_AC <= angle_BD) {
return {△ABC, △ACD};
} else {
return {△ABD, △BCD};
}直观理解:
好的分割(法向量对齐) 差的分割(法向量不对齐)
↗ ↗ ↗ ↙
╱╲ ╱╲
╱ ╲ ╱ ╲
╱────╲ ╱────╲
→ 表面平滑 → 表面有折痕完整数据流
╔═══════════════════════════════════════════════════════════╗
║ Mesh → O-Voxel ║
╠═══════════════════════════════════════════════════════════╣
║ ║
║ vertices ──┬──► intersect_qef() ──► voxels[] ║
║ faces ──┘ │ hash_table ║
║ │ means[] ║
║ │ intersected[] ║
║ ▼ qefs[] ║
║ face_qef() ║
║ │ ║
║ ▼ ║
║ boundry_qef() ║
║ │ ║
║ ▼ ║
║ QEF Solve ──────► dual_vertices[] ║
║ ║
╠═══════════════════════════════════════════════════════════╣
║ ║
║ 输出 O-Voxel = {voxels, dual_vertices, intersected} ║
║ ║
╚═══════════════════════════════════════════════════════════╝
╔═══════════════════════════════════════════════════════════╗
║ O-Voxel → Mesh ║
╠═══════════════════════════════════════════════════════════╣
║ ║
║ voxels ─────────┐ ║
║ dual_vertices ──┼──► face_from_dual_vertices() ║
║ intersected ────┘ │ ║
║ │ (找活跃边,连接 quad) ║
║ ▼ ║
║ quad_to_2tri() ║
║ │ (智能分割) ║
║ ▼ ║
║ 输出 Mesh = {vertices, faces} ║
║ ║
╚═══════════════════════════════════════════════════════════╝核心优势
| 特性 | 说明 |
|---|---|
| 无需 SDF | 直接从 Mesh 转换,跳过昂贵的距离场计算 |
| 支持开放网格 | boundry_qef 专门处理非封闭表面 |
| 亚体素精度 | 对偶顶点可在体素内连续移动 |
| 可逆转换 | Mesh ↔ O-Voxel 双向无损 |
| 智能分割 | 根据几何特征选择最优三角化 |
代码索引
| 功能 | 函数 | 位置 |
|---|---|---|
| 扫描线体素化 | intersect_qef() |
第 61-172 行 |
| 面 QEF 累加 | face_qef() |
第 175-288 行 |
| 边界 QEF 累加 | boundry_qef() |
第 291-383 行 |
| QEF 求解 | 主函数内 | 第 561-765 行 |
| 四边形分割 | quad_to_2tri() |
第 386-415 行 |
| 连接对偶顶点 | face_from_dual_vertices() |
第 418-458 行 |
本文基于 TRELLIS.2/o-voxel/src/convert/flexible_dual_grid.cpp 源码分析