搜索二叉树笔记模拟实现

定义和结构

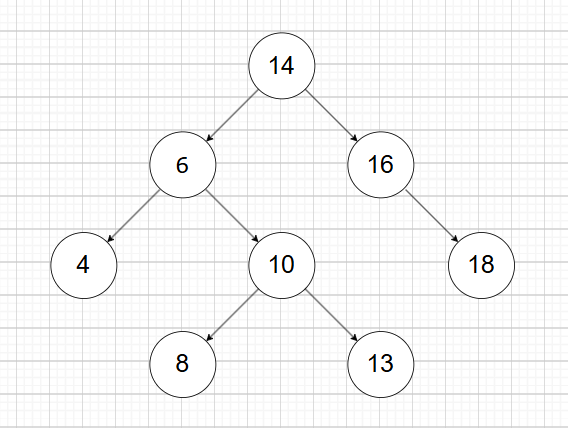
顾名思义是具有搜索作用的二叉树，搜索二叉树确保右子树节点值一定大于根节点，左子树节点值一定小于根节点 ，按照这种结构，搜索时类似二分查找 ：如果待查找值大于当前节点值，进入右子树，反之进入左子树。

时间复杂度：

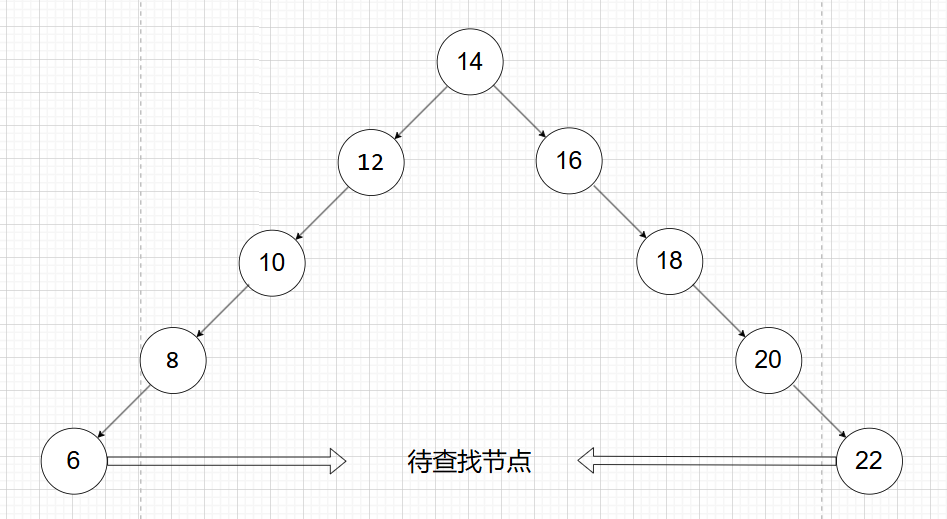
然而和二分查找有最坏情况一样，搜索二叉树最好的情况是logn，最坏的情况为n（下图所示）。后续的AVL树就是搜索二叉树的完善版本

模拟实现

只有删除的实现比较复杂，其它方法和堆类似，注释中有作说明。部分函数为了让接口更符合实际情况，就额外包了一层。

结构

和链表、堆类似，搜索二叉树分为单个节点的结构体和搜索二叉树主体，本体提供根节点和方法。

template<class T>
struct Treenode 
{
	typedef Treenode node;
	Treenode(){}
	Treenode(const T&value):_key(value),
	_left(nullptr)
	,_right(nullptr){}
	T _key;
	node* _left;
	node* _right;
};

template<class T>
class SearchTree {
	typedef Treenode<T> node;
public:
    //...方法
    node*root;
}

---

拷贝构造函数的实现

拷贝构造也就是克隆给到的树，同样利用前序遍历的方式，先让根节点指向拷贝的根节点，然后再走左右子树

SearchTree(const SearchTree<T>& k) {
	_root=equal(k._root);
}

node* equal(node* root) {//前序遍历
	if (root == nullptr) {
		return nullptr;
	}
	node* temp = new node(root->_key);//每次访问先开空间
	temp->_left = equal(root->_left);
	temp->_right = equal(root->_right);
	return temp;
}

---

析构函数的实现

析构函数和拷贝构造反过来，采用后序遍历方式，因为删了根节点就找不到左右子树了

~SearchTree() {
	clear(_root);
}

void clear(node* root) {//后序遍历，先把左右子树删干净再删根节点
	if (root == nullptr) {
		return;
	}
	clear(root->_left);
	clear(root->_right);
	delete root;
	root = nullptr;
}

---

插入的非递归和递归实现

递归版本：

bool insert(const T& value) {
	if (_root == nullptr) {//判断二叉树是否为空，是则直接插入
		_root= new node(value);
		return true;
	}
	node* parent = _root;
	node* child = _root;
	bool flag = false;//用于判断child应该插在parent右边还是左边的flag（直接写判断也可以）
	while (child) {
		if (child->_key > value) {
			parent = child;
			child = child->_left;
			flag = false;
		}
		else if(child->_key < value){
			parent = child;
			child = child->_right;
			flag = true;
		}
		else {//树中不应有值相同的两个节点
			return false;
		}
	} 
	if (!flag) {
		parent->_left = new node(value);
	}
	else {
		parent->_right = new node(value);
	}
	return true;
}

非递归实现版本，最重要的是使用节点指针的引用，否则插入无效

void insert_R(T&value) {//递归版本
	Insert(_root, value);
}

void Insert(node*&root,T&value) {
//引用的应用：如果直接对root这个临时变量修改没作用，所以参数加一个引用
	if (root==nullptr) {//找到nullptr说明在该条路线的末端，可以插入了
		root = new node(value);
		return;
	}

	if (root->_key>value) {//不满足条件就继续递归，根据大小选择走左走右
		Insert(root->_left, value);
	}
	else {
		Insert(root->_right, value);
	}
}

---

删除的非递归和递归实现

非递归实现需要判断的情况比较多：

1.被删除节点是否具有子节点？如果有，是一个还是两个子节点？

2.被删除节点是否为根节点？

3.被删除节点是其父节点的左子节点还是右子节点？

如果被删除节点没有子节点，直接删除即可

如果被删除节点有一子节点，直接让该节点的父节点指向子节点

如果被删除节点有左右子节点，此时需要用左子树的最大节点或右子树的最小节点 来替换被删除节点（这两个节点是最合理的末端节点），模拟实现时选择用左子树的最大节点来替换。同时这个操作可再次套用删除函数

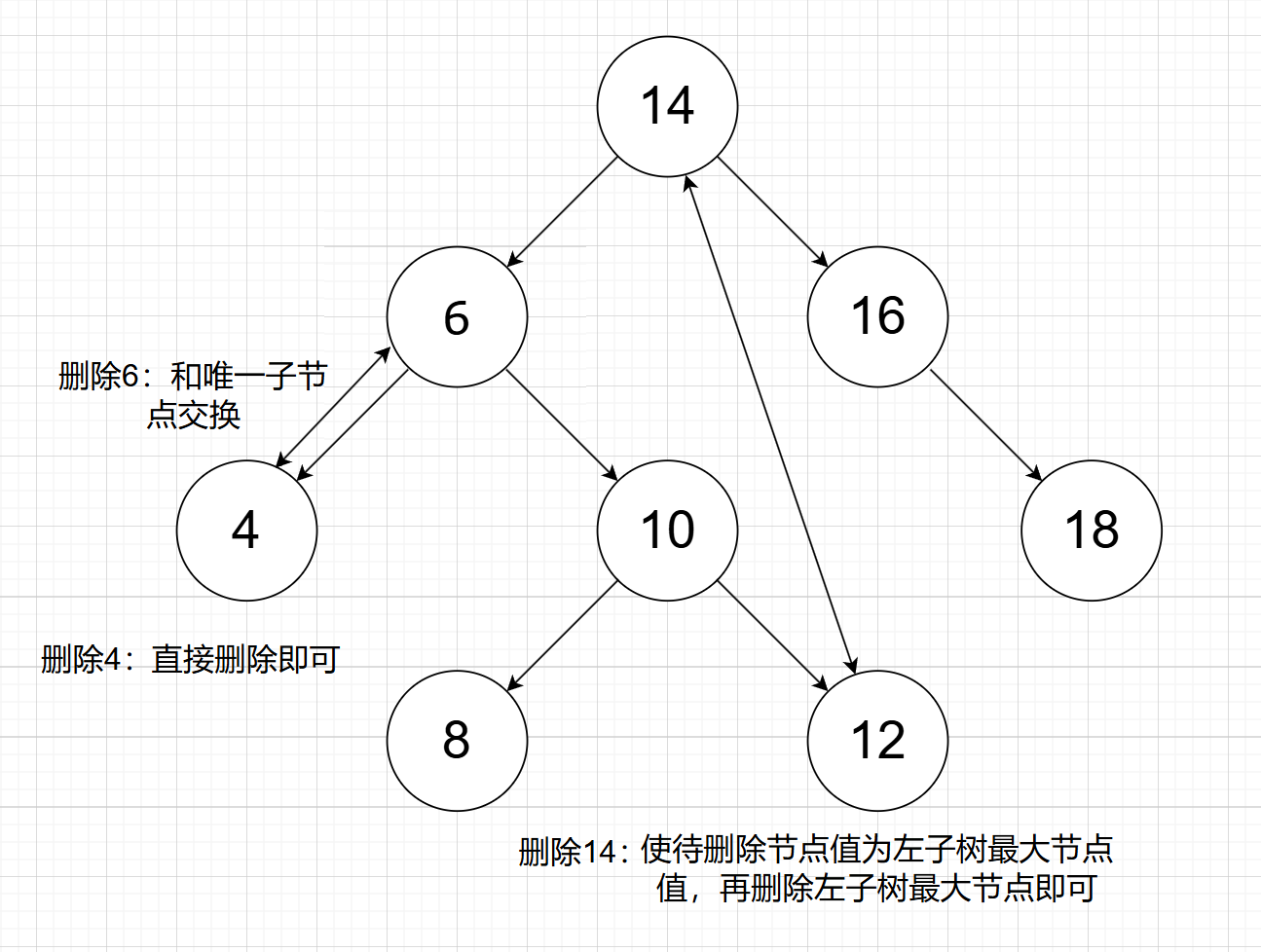
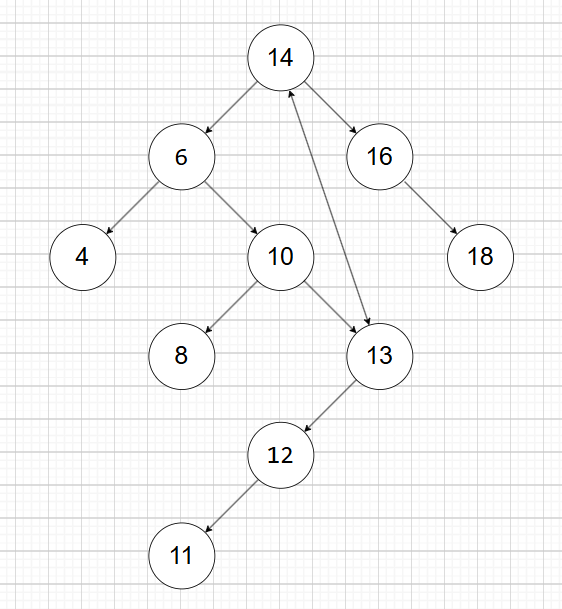
为了避免下面这种直接删掉13导致后面的节点丢失 的情况，需要存储13的值，再次调用erase函数先把13删除（自动拼接10和12）再把14换成13

void erase(const T& value) {
	//不能复用find，需要父节点
	node* parent = _root;
	node* child = _root;
	//node* temp = nullptr;//要不要temp？
	bool flag = false;//flag用于判断child是parent的左还是右节点
	while (child) {
		if (child->_key > value) {
			parent = child;
			child = child->_left;
			flag = false;
		}
		else if (child->_key < value) {
			parent = child;
			child = child->_right;
			flag = true;
		}
		//找到了需要删除的节点child
		else {
			//这个child没有或有一个子节点
			if (!(child->_left && child->_right)) {
				//这个节点是根节点
				if (_root->_key == value) {
					node* temp = _root;
					if (_root->_left) {
						_root = _root->_left;
					}
					else {
						_root = _root->_right;
					}
					delete temp;
				}
				//这个节点不是根节点
				else {
					//是否左子树存在
					if (child->_left) {
						if (!flag) {
							parent->_left = child->_left;
						}
						else {
							parent->_right = child->_left;
						}
					}
				//是否右子树存在（如果没有左右子树，依照下方也可以删除本节点）
					else {
						if (!flag) {
							parent->_left = child->_right;
						}
						else {
							parent->_right = child->_right;
									
						}
					}
					delete child;
				}
			}
			//这个child有两个节点
			else {
				//寻找左子树最大节点或右子树最小节点替代当前节点
				node* leftmax = child->_left;
				while (leftmax->_right) {
					leftmax = leftmax->_right;
				}
				T temp = leftmax->_key;
				erase(leftmax->_key);
				child->_key = temp;
			}
			break;
		}
	}
}

---

打印辅助函数

通过中序遍历可将搜索二叉树的节点值从小到大打印出来，可用于检查和调试

void print(node* target) {
	if (target == nullptr) {
		return;
	}
	print(target->_left);
	cout << target->_key << ' ';
	print(target->_right);
}