前言
在自动控制原理的教学中,自动控制系统的稳定性是重要的研究内容。系统稳定性通常可以通过代数判据或几何判据来判断,几何判据主要包括奈奎斯特稳定判据和伯德稳定判据。针对最小相位系统,采用奈奎斯特稳定判据判断稳定性时,要求奈奎斯特曲线不穿过(-1,j0)点且不能包围该点,系统才稳定;而采用伯德稳定判据时,通常情况下,增益裕度>0 时,系统稳定。然而,对于某些复杂的奈奎斯特曲线,判断奈奎斯特曲线是否包围(-1,j0)点可能存在一定难度,而采用伯德稳定判据时,当系统增益裕度< 0 时,系统却不能立即判断为不稳定系统.
最小相位系统实例
若控制系统为单位反馈系统,其开环传递函数为
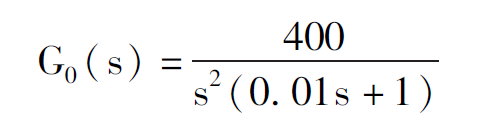
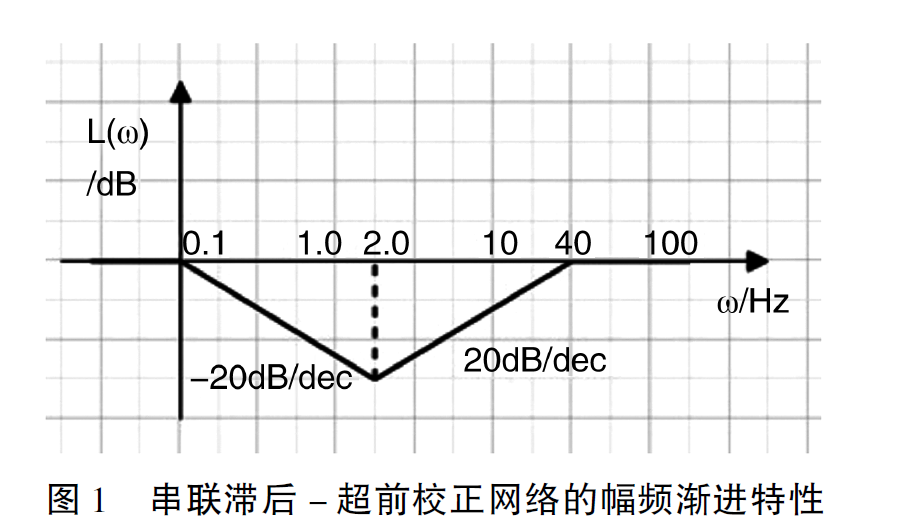
图1 为串联校正网络特性,由最小相位环节组成:
问:系统的稳定性如何?
为了讨论方便,本文在此将校正环节与原控制系统合并为一个新的系统,其开环传递函数为:
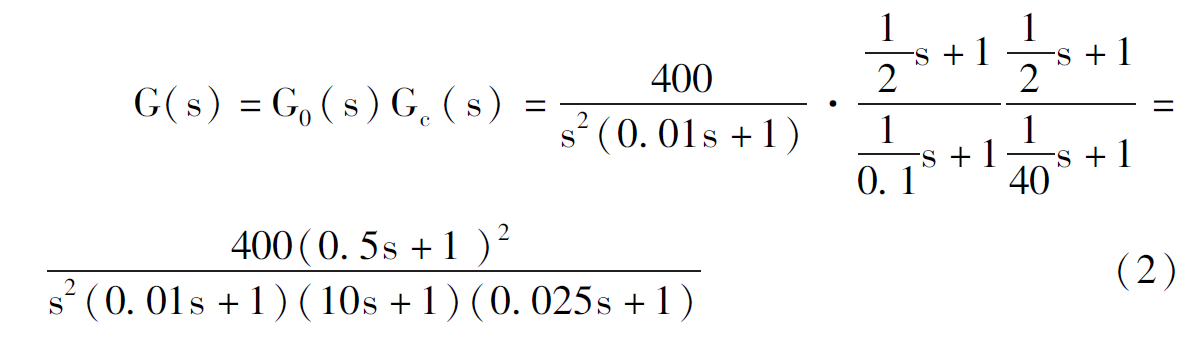
系统的频率特性:

其中:幅频特性为:
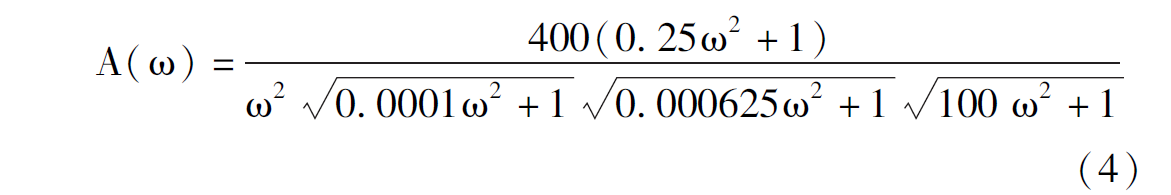
相频特性为:
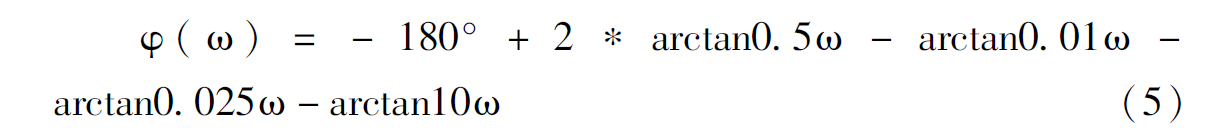
从式(2)可看出,系统的开环传递函数没有右极点、右零点以及延迟环节,属于最小相位系统。下面以这个系统为例,说明几何判据在系统稳定性分析中的应用情况。
二、用Matlab 得到的伯德图及其参数
依据幅频特性(4)和相频特性(5)可得到本系统的伯德图,采用Matlab 程序更为方便,伯德图如图2 所示。从图2 中可看出,系统的相位裕度Pm = 48.2°,ωc = 10rad/ s,增益裕度Gm = -19. 6dB,ωg = 2.05rad/ s。可见,系统的相位裕度为正,而增益裕度为负。
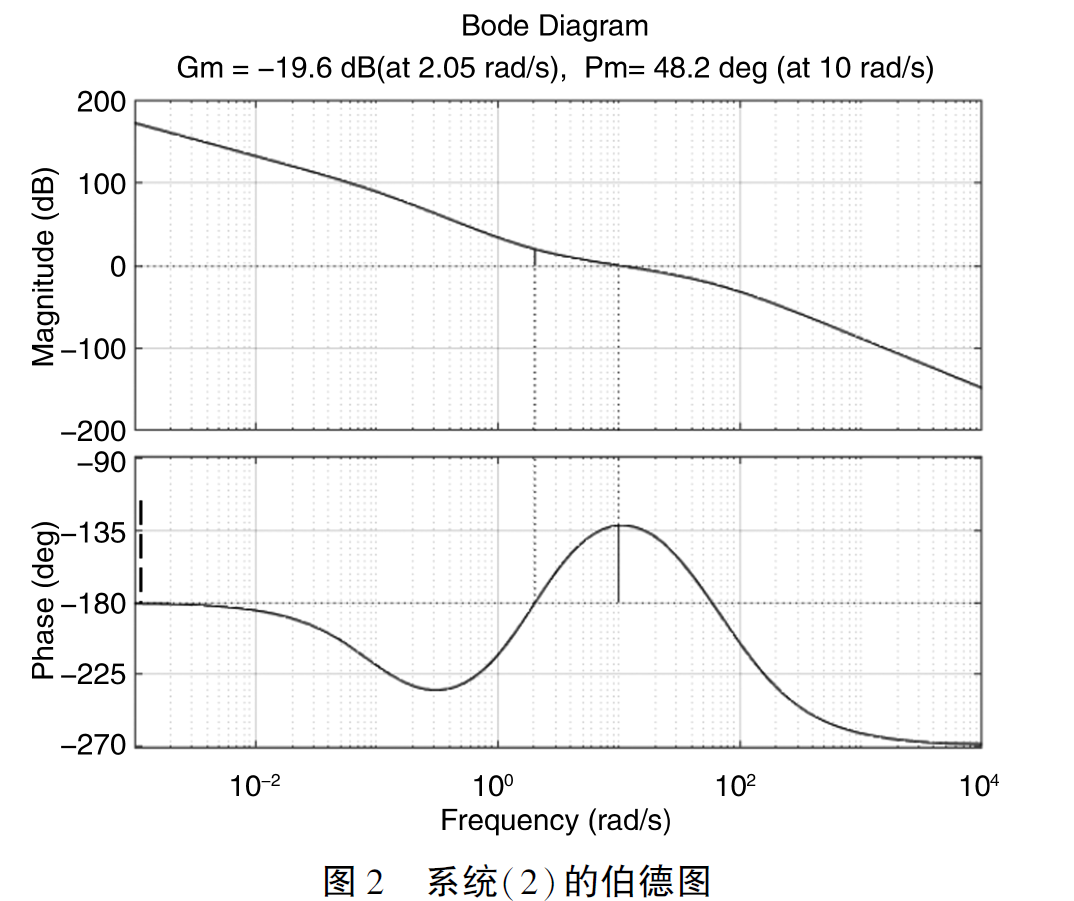
三、用Matlab 得到的奈奎斯特曲线
采用Matlab 程序可得到本系统频率范围- ∞ ~ + ∞ 的奈奎斯特图,如图3(a)所示。但曲线对
( - 1,j0)点的包围情况无法识别,须采取措施,明确( -1,j0)点与曲线的关系,只取靠近该点的局部曲线,如图3(b)所示,可清楚看出奈奎斯特曲线和( -1,j0)点的关系。图中十字符号" + "代表( - 1,j0)点的位置。
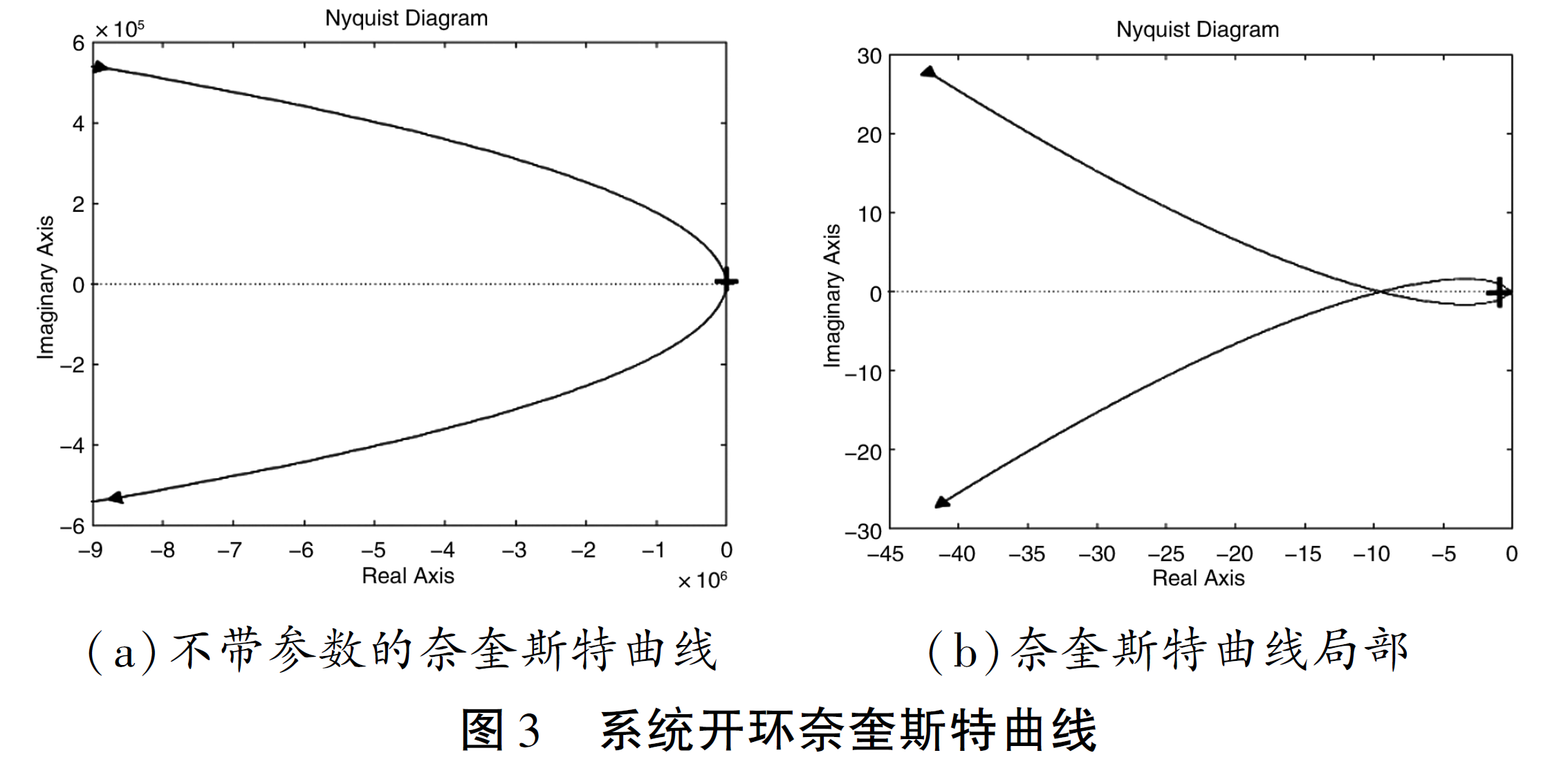
四、稳定性讨论
从图2 可看出,本系统的相位裕度Pm = 48.2°,增益裕度Gm = -19.6dB,系统的相位裕度、增益裕度符号相反,这种情况可能导致学生对系统的稳定性产生困惑和分歧。
从图3 看出,(-1,j0)点似乎被奈奎斯特曲线包围一圈,按照奈奎斯特稳定判据,对于最小相位系统而言,本闭环系统应该是不稳定的系统。然而这一结论并不准确。对于这种复杂的系统和存在分歧的情况,可以从不同的角度和判据进行分析,以便更清晰地判断系统的稳定性。
(一)奈奎斯特稳定判据。根据奈奎斯特稳定判据,当频率ω 从- ∞→ + ∞时,奈奎斯特闭合曲线不穿过( -1,j0)点且包围( -1,j0)点的圈数标记为N(逆时针包围为正,顺时针为负)。开环传递函数右极点的个数为P,闭环系统右极点的个数为Z。根据公式

如果Z =0,闭环系统稳定,否则,系统不稳定.
由式(6)可知,对于最小相位系统P =0,若要求Z =0,必须有N =0,即开环奈奎斯特闭合曲线不能包围( - 1,j0)点,然而,从图3(b)可明显看出( - 1,j0)点被曲线"包围"一圈,即N =1,那么该闭环系统就是一个不稳定的系统吗?
在奈奎斯特稳定性判据中,需要注意到曲线包围( - 1,j0)点,指的是在频率从- ∞→ + ∞的变化过程中,开环奈奎斯特闭合曲线包围( -1,j0)点的情况,而在本例中,在ω =0 处出现了断点,不是一般意义上的闭合曲线,难以判断闭合曲线包围( -1,j0)点的情况。对于本例来说,系统是个II 型系统,需要在ω =0 + 处逆时针补充90° × 2 = 180°的半圆曲线,如图4(a)中的虚线和点划线所示。这意味着我们需要形成一个新的曲线,当ω =0 + 到+ ∞ 变化时,这个新的曲线包括虚线(①)和ω =0 + → + ∞(②)两段。根据奈奎斯特曲线关于实轴对称的特性,我们可以对称补足ω = 0 - 到- ∞ 的奈奎斯特曲线,如图4(a)中的点划线(④)所示。因此,当观察ω 从- ∞ 到+ ∞ 变化时,奈奎斯特闭合曲线就变成从原点开始沿着ω = - ∞→0 -(③)、点划线(④)、虚线(①)、ω = 0 + → + ∞(②)回到原点的一个闭合曲线。
此时,再观察图4(a),几乎所有人都认为曲线"包围"( -1,j0)点两圈,即N = 2。根据式(6),本系统显然是一个不稳定系统。事实果真如此吗? 这时就需要正确理解奈奎斯特
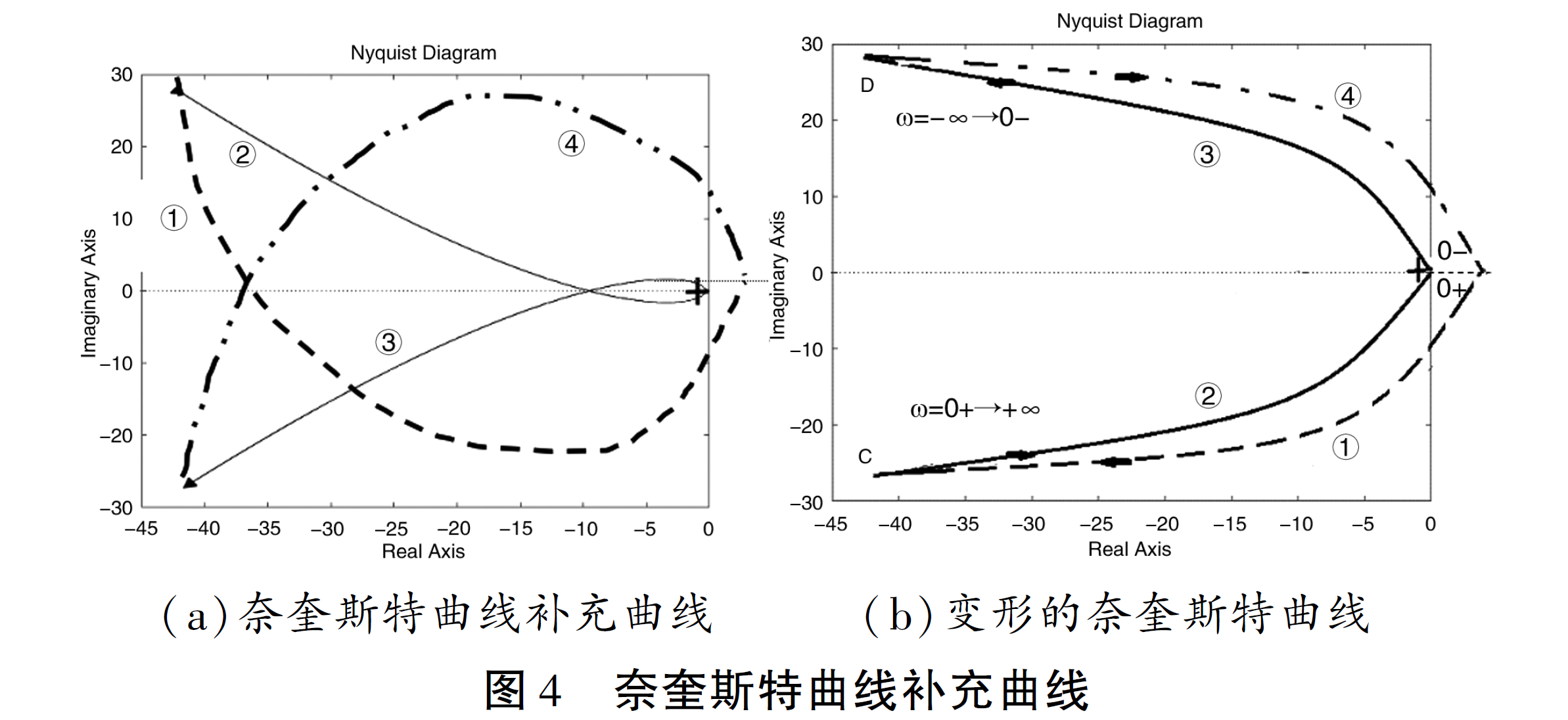
如果把线段①和线段②的连接处逆时针转到图4(b)的C点,把线段③和线段④连接处顺时针转到图4(b)的D 点。
显然,在这样的变化过程中,闭合曲线包围( - 1,j0)点的性质并没有发生变化,但可清晰地看出,( - 1,j0)点在闭合曲线之外,即闭合曲线并不包围( -1,j0),此时,N =0。这时再看奈奎斯特稳定判据中闭合曲线点"包围"( - 1,j0)点的真正含义,即点( -1,j0)必须在闭合曲线内,才能算"包围",而不是说只要该点被曲线围着就叫"包围"。
由此可以看出,在ω 从- ∞ 到+ ∞ 变化时,奈奎斯特曲线并不包围( -1,j0),即N =0,因此Z = P - N =0,该闭环系统是稳定的。
由于奈奎斯特稳定判据是根据频率ω 从- ∞到+ ∞的过程中,曲线包围( -1,j0)点的圈数来判断的。在使用Matlab 软件绘制奈奎斯特曲线时,如果不带参数,得到的即ω 从- ∞到+ ∞的曲线,如图3 所示。即使局部放大如图3(b)或者补足曲线其余部分如图4(a),在判断奈奎斯特曲线是否包围( -1,j0)点时,仍无法得到准确的N 值,从而对系统闭环稳定性判断错误。
但正如前文所说,奈奎斯特曲线是关于实轴对称的,因此可以只研究曲线的一半即可了解整个曲线的性质。在教学过程中,主要关注的是ω 从0 + → + ∞的曲线,即正频率段的奈奎斯特曲线。使用Matlab 软件,通过参数设置绘制频率为正的奈奎斯特曲线,如图5 中实线所示。接下来,利用图5 进行系统稳定性分析。
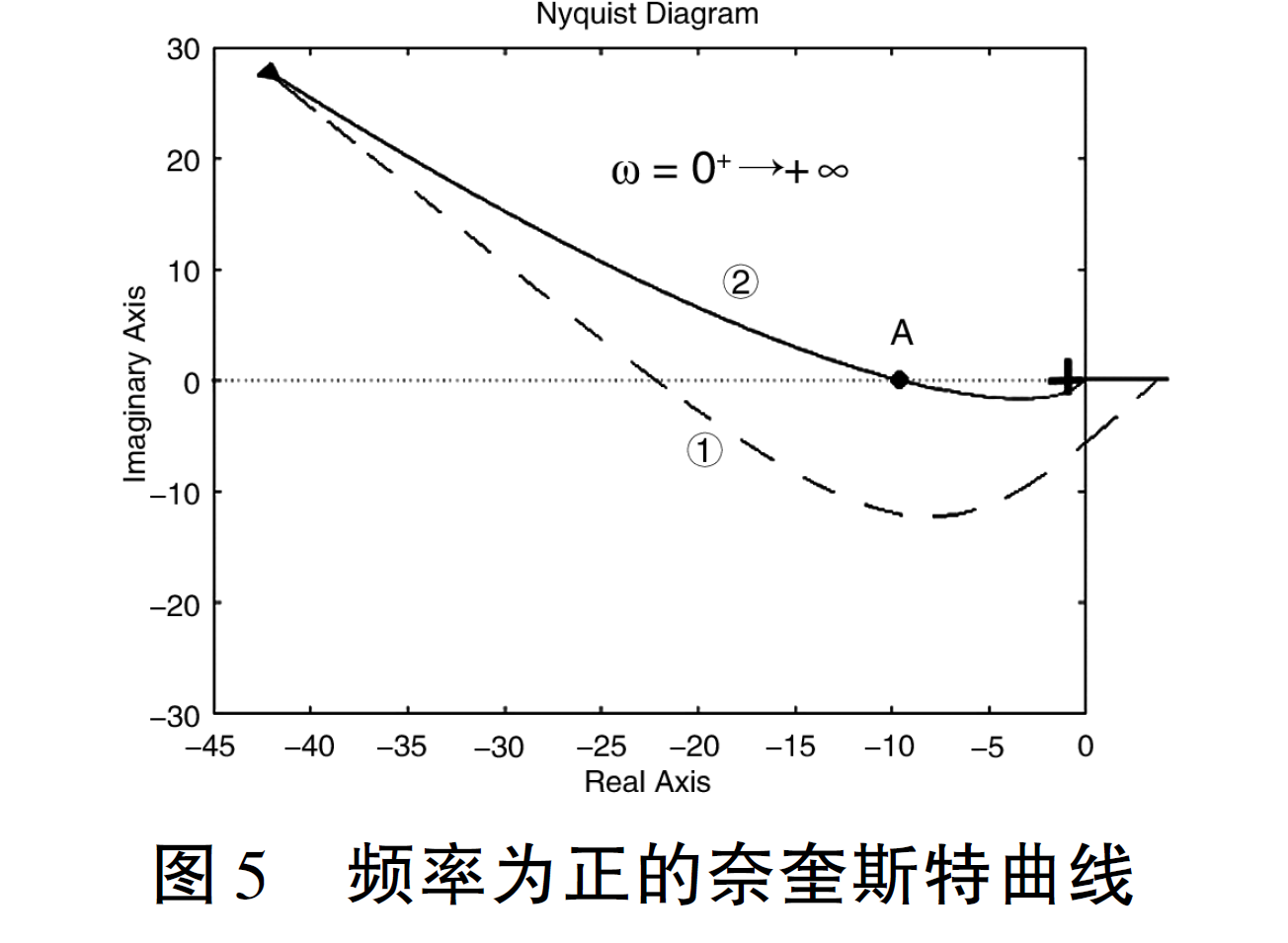
由于本系统是II 型系统,仍需要在ω = 0 + 处逆时针补充90° ×2 =180°的半圆曲线,如图5 中的虚线所示,补过之后,在做稳定性判断时,就认为ω = 0 + 的曲线起点位于正实轴部分,从图5 中可看出,当ω 从0 + → + ∞时,曲线是从正实轴部分开始经过虚线(①)、ω =0 + → + ∞(②)的部分,并趋于原点,在这个图上可清楚地看出,( -1,j0)点并不在奈奎斯特闭合曲线包围的范围之内,即N'=0(此处的圈数用N'表示,表明与N 的不同),奈奎斯特稳定判据为:
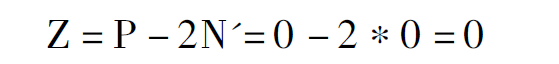
由此,可判断该闭环系统是稳定的系统。从以上分析可见,在使用奈奎斯特稳定判据时,使用ω 从0 + → + ∞的曲线,在判断N(或N')时,更清晰简明一点,更易对系统稳定性进行分析。
(二)伯德稳定判据。伯德稳定判据指出,如果开环系统具有P 个开环极点位于右半平面,则闭环系统稳定的充要条件是:在对数幅频特性为正的所有频段内,对数相频特性与-180°相位线的正负穿越次数之差为P/2。根据这一判据,对于最小相位系统,通常可以得到稳定性与相位裕度、增益裕度的关系如下:当相位裕度Pm > 0 时,系统稳定;当增益裕度Gm >0 时,系统稳定。本系统的相位裕度Pm =48.2° > 0,表明系统是稳定的。然而,增益裕度Gm =-19.6dB <0,这使得系统的稳定性无法确定。
对于这个系统,简单地使用伯德稳定判据的推论,不能得到系统是否稳定的明确结论,需要采用其它办法。由于系统是II 型系统,需要在相频曲线的左端向上补90° ×2 =180°,如图2 中的虚线所示。在采用伯德判据进行系统稳定性判断时,应该认为系统相频特性曲线是从0°→180°再连接到实际相频特性曲线。
在幅频特性曲线上对应0dB 的频率ω =10rad/ s,即在相频特性曲线上看ω = 10rad/ s 左边曲线穿越- 180°的情况。在相频特性的最左端,曲线由0°向下穿越到- 180°下方,即有一次负穿越,N- = 1。在ω = 2. 05rad/ s 处,相频特性曲线由- 180°下方向上穿越到- 180°上方,即有一次正穿越,N+ = 1。对于最小相位系统,P =0。故
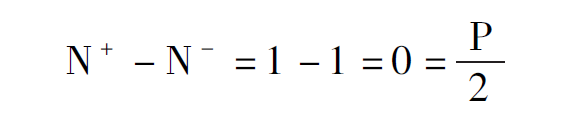
故该系统稳定。
结语
在使用奈奎斯特稳定判据来判断系统稳定性时,需要全面考虑曲线是否包围了( - 1,j0)点,
并且要真正理解"包围"的含义。如果采用全频率段曲线判断不清楚时,可以考虑采用正频率段的曲线,并对稳定判据做适当的修改。在采用伯德稳定判据时,需要全面考虑系统的开环增益裕度和相位裕度,不能简单地依据单一指标来判断系统的稳定性。因此,对于不同的稳定判据,需要全面考虑相关因素,并在实际判断中灵活运用,以确保对系统稳定性的准确判断。