逻辑回归实例问题解决（LogisticRegression）

一、k折交叉验证（评判选定不同的C值）

将某个数据集分为训练集和测试集，将训练集再划分为K份，对于这K份训练集中的每一份都选择一次作为验证集（val），其余K-1份作为训练集，（避免将训练集再次切分，使得训练数据变少）

进行k 次完整的「训练 + 验证」循环，每次循环都包含一次独立的模型训练，每次训练后都要进行一次评分（scoring）（eg：recall），将k次评分累加求和除以k得到平均值，作为最终结果，对比不同的结果（依据你选择的评分）来选定C值。

scores = []
c_range = [0.01, 0.1, 1, 10, 100]

for i in c_range:
    lr = LogisticRegression(
        C=i,
        penalty='l2',
        solver='lbfgs',
        random_state=1000,
        max_iter=1000
    )
    score = cross_val_score(lr, x_train_scaled, y_train_balanced, cv=8, scoring='recall')
    scores_mean = score.mean()
    scores.append(scores_mean)
    print(scores_mean)

from sklearn import metrics
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression


data = pd.read_csv('./creditcard.csv')

# 3. 数据预处理（删除无用列）
data = data.drop(['Time'], axis=1)  # 删除Time列

# 4. 拆分特征和标签
data_x = data.drop(labels='Class', axis=1)
data_y = data['Class']

# 5. 划分训练集和测试集（先拆分，再处理训练集的样本不均衡）
x_train, x_test, y_train, y_test = train_test_split(
    data_x, 
    data_y, 
    test_size=0.3, 
    random_state=1000 
)

# 组合训练集的特征与标签（方便下采样）
x_train_w = pd.DataFrame(x_train, columns=data_x.columns)  # 保持特征列名
x_train_w['Class'] = y_train  # 拼接标签列
data_train = x_train_w

# 分离多数类（Class=0，正常样本）和少数类（Class=1，少数样本）
normal_samples = data_train[data_train['Class'] == 0]
abnormal_samples = data_train[data_train['Class'] == 1]

# 设置随机种子（保证下采样结果可复现）
np.random.seed(seed=4)

# 下采样：多数类样本数量缩减到与少数类一致
normal_samples_downsampled = normal_samples.sample(
    n=len(abnormal_samples),  # 抽取数量=少数类样本数
    replace=False  # 不重复抽取
)

# 拼接下采样后的多数类和少数类，得到平衡的训练集
data_balanced = pd.concat(
    [normal_samples_downsampled, abnormal_samples], 
    ignore_index=True  # 重置索引，避免重复
)

# 打乱平衡后的训练集（避免样本分布集中）
data_balanced = data_balanced.sample(frac=1, random_state=4).reset_index(drop=True)

# 从平衡训练集中拆分特征和标签
x_train_balanced = data_balanced.drop(labels='Class', axis=1)
y_train_balanced = data_balanced['Class']


scaler = StandardScaler()
x_train_scaled = scaler.fit_transform(x_train_balanced)  # 拟合平衡训练集
x_test_scaled = scaler.transform(x_test)  # 仅转换测试集

# 7. 遍历不同C值，寻找最优正则化参数
scores = []
c_range = [0.01, 0.1, 1, 10, 100]

for i in c_range:
    lr = LogisticRegression(
        C=i,
        penalty='l2',
        solver='lbfgs',  
        random_state=1000,
        max_iter=1000
    )
    # 交叉验证（基于平衡训练集）
    score = cross_val_score(lr, x_train_scaled, y_train_balanced, cv=8, scoring='recall')
    scores_mean = score.mean()
    scores.append(scores_mean)
    print(f"C={i} 时，交叉验证召回率平均值：{scores_mean}")

# 8. 选择最优C值
c_optimal = c_range[np.argmax(scores)]
print(f"\n最优 C 值：{c_optimal}")

# 9. 用最优C值训练最终模型（基于平衡训练集）
lr_optimal = LogisticRegression(
    C=c_optimal,
    penalty='l2',
    solver='lbfgs',
    random_state=1000,
    max_iter=1000
)
lr_optimal.fit(x_train_scaled, y_train_balanced)

# 10. 测试集预测与评估
test_predict = lr_optimal.predict(x_test_scaled)
print("\n模型在测试集上的分类报告：")
print(metrics.classification_report(y_test, test_predict))

二、数据不均衡问题解决方案

2.1 下采样

不同标签的样本数量差异大，以样本量少的为基准数量，在样本量多的样本中随机选择与基准数量相同的样本，从而构建一个类别平衡的训练集。

positive_eg = data_train[data_train['Class'] == 0]
negative_eg = data_train[data_train['Class'] == 1]


positive_eg = positive_eg.sample(n=len(negative_eg))

data_train = pd.concat([positive_eg, negative_eg])

from sklearn import metrics
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression

from imblearn.over_sampling import SMOTE



data = pd.read_csv('./creditcard.csv')

# 3. 数据预处理（删除无用列）
data = data.drop(['Time'], axis=1)  # 删除Time列

# 4. 拆分特征和标签
data_x = data.drop(labels='Class', axis=1)
data_y = data['Class']

# 5. 划分训练集和测试集（先拆分，再对训练集做过采样）
x_train, x_test, y_train, y_test = train_test_split(
    data_x, 
    data_y, 
    test_size=0.3, 
    random_state=1000  # 固定随机种子
)



# 初始化SMOTE（random_state保证结果可复现）
oversampler = SMOTE(random_state=0)
# 对训练集特征+标签做过采样（生成平衡的训练集）
os_x_train, os_y_train = oversampler.fit_resample(x_train, y_train)


scaler = StandardScaler()
# 对过采样后的训练集做拟合+转换
os_x_train_scaled = scaler.fit_transform(os_x_train)
# 测试集仅用训练集的标准化器转换
x_test_scaled = scaler.transform(x_test)


# 7. 遍历不同C值，基于过采样训练集找最优参数
scores = []
c_range = [0.01, 0.1, 1, 10, 100]

for i in c_range:
    lr = LogisticRegression(
        C=i,
        penalty='l2',
        solver='lbfgs',
        random_state=1000,
        max_iter=1000
    )
    # 交叉验证：传入过采样+标准化后的训练集
    score = cross_val_score(lr, os_x_train_scaled, os_y_train, cv=8, scoring='recall')
    scores_mean = score.mean()
    scores.append(scores_mean)
    print(f"C={i} 时，交叉验证召回率平均值：{scores_mean}")


# 8. 选择最优C值
c_optimal = c_range[np.argmax(scores)]
print(f"\n最优 C 值：{c_optimal}")


# 9. 用最优C值训练最终模型（基于过采样+标准化的训练集）
lr_optimal = LogisticRegression(
    C=c_optimal,
    penalty='l2',
    solver='lbfgs',
    random_state=1000,
    max_iter=1000
)
lr_optimal.fit(os_x_train_scaled, os_y_train)

# 10. 测试集预测与评估
test_predict = lr_optimal.predict(x_test_scaled)
print("\n模型在测试集上的分类报告：")
print(metrics.classification_report(y_test, test_predict))

2.1 过采样

不同标签的样本数量差异大，主动增加少数类样本的数量，让少数类样本的数量与多数类保持一致，从而构建类别平衡的训练集，让模型能充分学习到少数类的特征，避免因少数类样本太少而被模型忽略。

from imblearn.over_sampling import SMOTE 

oversampler = SMOTE(random_state=0)
os_x_train, os_y_train = oversampler.fit_resample(x_train_w, y_train_w)

三、正则化惩罚（防止过拟合）

损失函数：

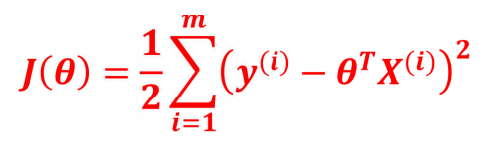
正则化惩罚：

LogisticRegression(penalty='l2', dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver='liblinear', max_iter=100, multi_class='ovr', verbose=0, warm_start=False, n_jobs=1)

在LogisticRegression()参数中通过**solver='liblinear'**来指定逻辑回归损失函数的优化方法。

C：正则化强度。为浮点型数据。正则化系数λ的倒数，float类型，默认为1.0。必须是正浮点型数。像SVM一样，越小的数值表示越强的正则化。