简介
ResNet(残差网络,Residual Network)是由何恺明、张祥雨、任少卿和孙剑等人于2015年提出的一种深度卷积神经网络架构,其核心创新是残差连接(或称跳跃连接,shortcut connection),通过引入恒等映射路径,使网络能够学习输入与输出之间的残差(即F(x)=H(x)+x,从而有效缓解了深度网络中的梯度消失和网络退化问题,使得训练上百层甚至上千层的神经网络成为可能。
残差块(残差函数F(x) )
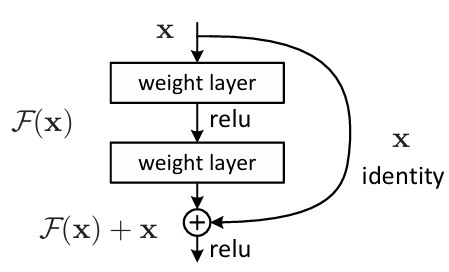
输入x:输入特征图(feature map),进入残差块。通常来自前一层的输出。
主路径(Main Path):F(x)包含两个"weight layer"(即卷积层),中间夹着 ReLU 激活函数。这个路径负责学习输入与目标之间的"残差"变换。
输出为F(x),表示希望学习到的"变化量"。
捷径连接(Shortcut Connection):输入x 直接通过一条"跳跃"路径传递到加法操作。标注为 "identity",意思是不做任何变换,直接将原始输入传入。这条路径的作用是实现恒等映射,防止信息丢失。
加法操作(⊕)将主路径的输出F(x) 与捷径路径的输入x 进行元素级相加(element-wise addition)。得到的结果是:F(x)+x
经过加法后,再经过一次 ReLU 激活函数,作为该残差块的输出,传递给下一层。
为什么这样设计?
(1)在极深的网络中,随着层数增加,训练误差可能上升,即"网络退化"。
(2)残差连接允许网络轻松地"跳过"某些层,保持原始信息流动。
(3)使得训练数百甚至上千层的网络成为可能。
原理
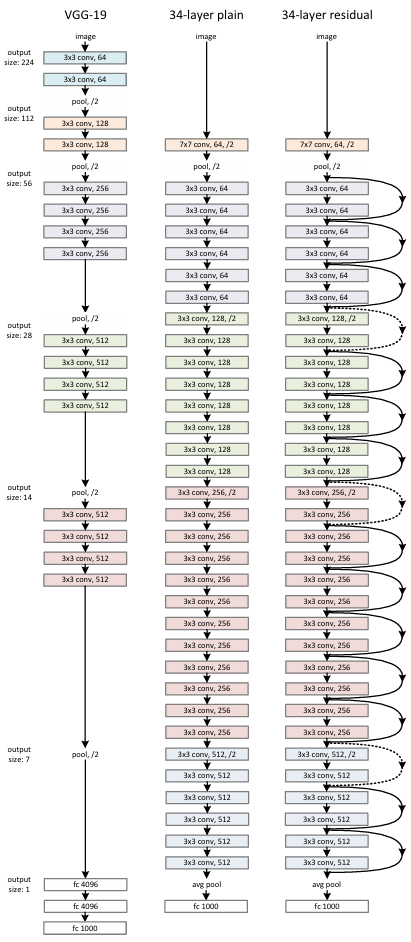
在 ResNet 提出之前,人们发现随着网络层数增加 ,训练误差反而上升(不是过拟合,而是连训练集都拟合不好);这种现象称为 "退化问题",不同于梯度消失/爆炸(那些可通过 BatchNorm、初始化等缓解)。
例如:一个 56 层的 plain network(普通卷积堆叠)比 20 层的性能更差,尽管它理论上具有更强的表达能力。
当网络很深时,直接学习目标映射 H(x) (如从输入到输出的复杂函数)变得极其困难。优化器很难找到合适的参数使得多层非线性变换恰好等于理想映射。
ResNet 不再让网络直接拟合目标映射H(x) ,而是让它拟合残差函数:H(x)=x+F(x) ⇒ F(x)=H(x)−x。如果最优映射接近恒等映射(即H(x)≈x ),那么残差F(x)≈0 。学习一个接近零的函数,比学习一个复杂的恒等映射要容易得多
恒等捷径连接(Identity Shortcut)
残差块通过 加法操作 将输入x 直接传递到输出端。这形成了一个"信息高速公路",即使中间的权重层全为零,输出仍为x 。
因此,网络永远不会比浅层网络表现更差------最坏情况就是残差部分学成零,退化为恒等映射。
梯度传播稳定(缓解梯度消失问题)
在普通的深度神经网络中,信息要一层一层地向前传递(前向传播),误差也要一层一层地向后传递(反向传播)。当网络非常深时,每一层的梯度都要乘以前面所有层的导数。如果这些导数普遍小于 1(比如因为激活函数饱和或权重初始化不当),那么梯度就会像"雪球越滚越小",传到前面几层时几乎变成零------这就是梯度消失。结果就是:浅层几乎学不到东西,整个网络难以训练。
而 ResNet 引入了一个巧妙的设计:让输入信号可以直接"跳过"中间的层,通过一条捷径(shortcut)直接加到输出上。在反向传播时,这个设计带来一个关键好处:误差信号在回传时,不仅可以走中间那些复杂的卷积层路径,还可以直接通过这条捷径原路返回。
换句话说,即使中间的卷积层因为太深而导致它们的梯度变得非常微弱,总有一条"高速公路"能让梯度几乎无损地传回前面的层 。因此,ResNet 中的每一层都能接收到较强的梯度信号,参数可以有效更新,即使网络有上百层甚至上千层,也不会因为梯度消失而无法训练。
示例