深度学习速成：损失函数与反向传播

1.LOSS函数

Loss=（目标值-实际值）的绝对值 +.....之和

1.1作用：

1.计算实际输出与目标之间的关系

2.为我们更新输出提供一定的依据

1.2 举例

1.2.1 torch.nn.L1loss

使用方法：

注意输入输出的shape是相同的

数学公式：

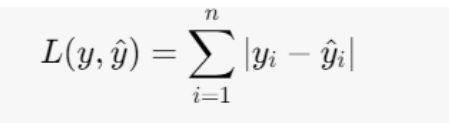
python 复制代码

import torch
from torch import nn


inputs=torch.tensor([1,2,3]).float()#要使用浮点数
targets=torch.tensor([1,2,5]).float()

inputs =torch.reshape(inputs,(1,1,1,3))
targets=torch.reshape(targets,(1,1,1,3))

loss=torch.nn.L1Loss()
ressult=loss(inputs,targets)

print(ressult)

输出为tensor(0.6667) 因为作差后相加再除以3 即三分之二。

1.2.2 torch.nn.MSELoss

python 复制代码

import torch
from torch import nn



inputs=torch.tensor([1,2,3]).float()
targets=torch.tensor([1,2,5]).float()

inputs =torch.reshape(inputs,(1,1,1,3))
targets=torch.reshape(targets,(1,1,1,3))

loss=torch.nn.L1Loss()
ressult=loss(inputs,targets)

loss_mse=torch.nn.MSELoss()
ressult_mse=loss_mse(inputs,targets)

print(ressult,ressult_mse)

输出结果为tensor(1.3333) 也就是三分之四

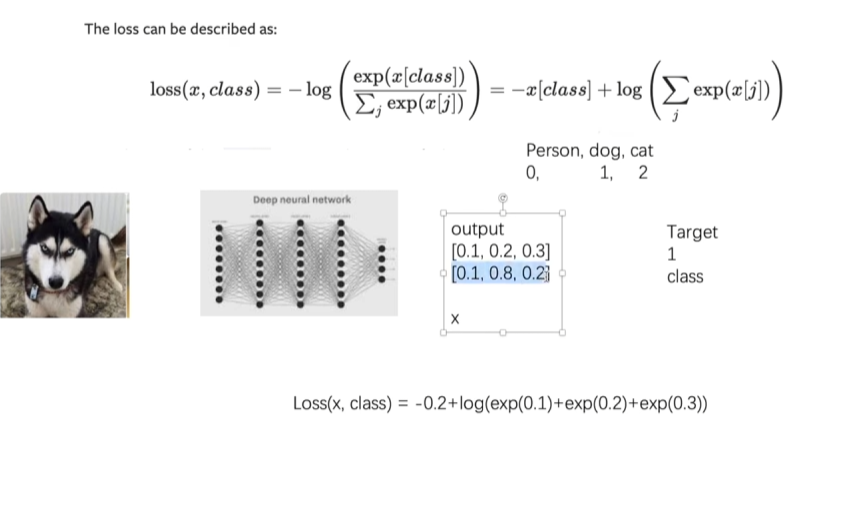
1.2.3 交叉熵函数

处理分类问题时常用

数学公式：

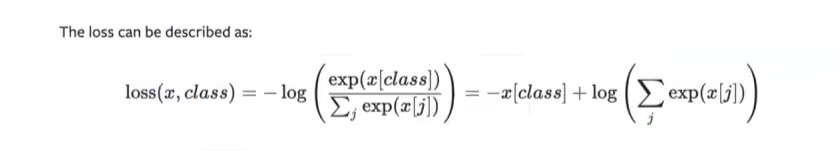
python 复制代码

x=torch.tensor([0.1,0.2,0.3])
y=torch.tensor([1])

x=torch.reshape(x,(1,3))

loss_ce=nn.CrossEntropyLoss()
result_ce=loss_ce(x,y)
print(result_ce)

输出结果为tensor(1.1019)

2.反向传播

反向传播算法利用链式法则，通过从输出层向输入层逐层计算误差梯度，高效求解神经网络参数的偏导数，以实现网络参数的优化和损失函数的最小化。

计算出loss后对loss进行反向传播(backward)梯度下降法

python 复制代码

Tudui=tudui()

for data in dataloder:
    imgs,targets=data
    outputs=Tudui(imgs)
    result_loss=loss(outputs,targets)
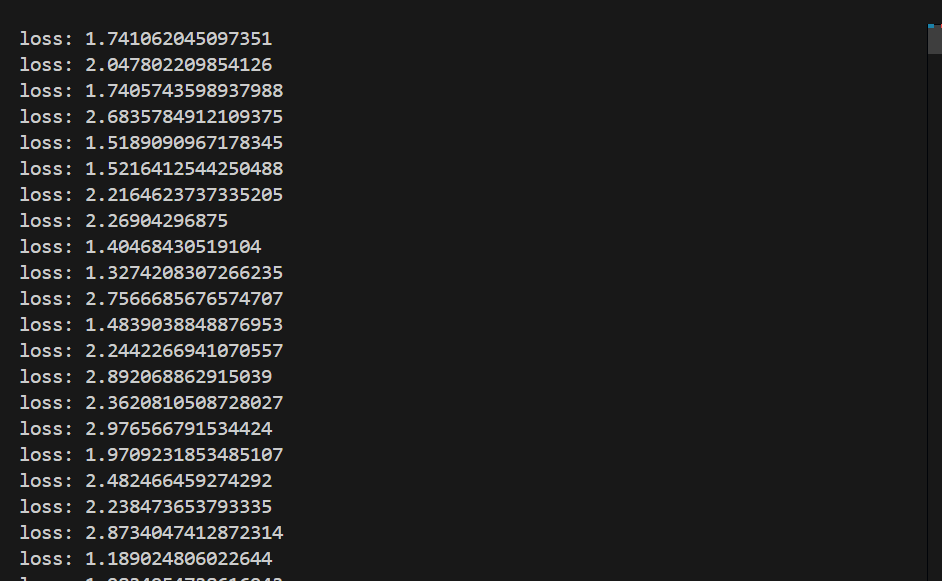
    print("loss:",result_loss.item())
    result_loss.backward()#反向传播

3.优化器

python 复制代码

loss=torch.nn.CrossEntropyLoss()
Tudui=tudui()
optim=torch.optim.SGD(Tudui.parameters(),lr=0.01)#定义优化器 随机梯度下降

for data in dataloder:
    imgs,targets=data
    outputs=Tudui(imgs)
    result_loss=loss(outputs,targets)
    optim.zero_grad()#优化器梯度清零
    result_loss.backward()#反向传播
    optim.step()#优化器更新参数

先定义优化器

得到loss后进行梯度清零反向传播优化器更新参数

结果