【论文解读】Transformers are RNNs

文章目录

概览
一、Transformers
二、线性化注意力
三、因果掩码
- （一）梯度计算
- - [2. 对K的梯度](#2. 对K的梯度)
  - [3. 对V的梯度](#3. 对V的梯度)
  - [4. 小节](#4. 小节)
- （二）训练和推理
[四、Transformers are RNNs](#四、Transformers are RNNs)
五、总结

概览

Transformer 在多项任务中表现出色，但因其对输入序列长度的二次复杂度计算，在处理极长序列时速度过慢。为解决此问题，本文将自注意力表示为核特征映射的线性点积，利用矩阵乘法的结合律，将计算复杂度从 O ( N 2 ) O (N^2) O(N2) 降至 O ( N ) O (N) O(N)，大幅加速了自回归 Transformer，并揭示其与循环神经网络（RNN）的关联。

原文链接：Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention

一、Transformers

设 x ∈ R N × F x \in \mathbb{R}^{N \times F} x∈RN×F 表示一个由 N N N 个维度为 F F F 的特征向量组成的序列。Transformer 是一个由 L L L 个 transformer 层 T 1 ( ⋅ ) , ... , T L ( ⋅ ) T_1(\cdot), \ldots, T_L(\cdot) T1(⋅),...,TL(⋅) 组成的函数 T : R N × F → R N × F T : \mathbb{R}^{N \times F} \to \mathbb{R}^{N \times F} T:RN×F→RN×F，每层定义如下：

T l ( x ) = f l ( A l ( x ) + x ) \begin{equation} T_l(x) = f_l(A_l(x) + x) \end{equation} Tl(x)=fl(Al(x)+x)

其中， f l ( ⋅ ) f_l(\cdot) fl(⋅) 独立地变换每个特征，通常通过一个小的两层前馈网络实现。 A l ( ⋅ ) A_l(\cdot) Al(⋅) 是自注意力函数，是 Transformer 中唯一跨序列作用的部分。

输入序列 x x x 通过三个矩阵 W Q ∈ R F × D W_Q \in \mathbb{R}^{F \times D} WQ∈RF×D、 W K ∈ R F × D W_K \in \mathbb{R}^{F \times D} WK∈RF×D 和 W V ∈ R F × M W_V \in \mathbb{R}^{F \times M} WV∈RF×M 投影为对应的表示 Q Q Q、 K K K 和 V V V。所有位置的输出 A l ( x ) = V ′ A_l(x) = V' Al(x)=V′ 计算如下：

Q = x W Q , K = x W K , V = x W V , A l ( x ) = V ′ = softmax ( Q K ⊤ D ) V \begin{equation} \begin{aligned} Q &= xW_Q, \\ K &= xW_K, \\ V &= xW_V, \\ A_l(x) &= V' = \text{softmax}\left(\frac{QK^{\top}}{\sqrt{D}}\right)V \end{aligned} \end{equation} QKVAl(x)=xWQ,=xWK,=xWV,=V′=softmax(D QK⊤)V

公式 ( 2 ) (2) (2) 即 softmax 注意力，它的相似度得分是 query 和 key 的点积的指数。进一步，我们可以使用任意相似度函数，写出一个通用的注意力公式如下：

V i ′ = ∑ j = 1 N sim ( Q i , K j ) V j ∑ j = 1 N sim ( Q i , K j ) \begin{equation} V'i = \frac{\sum{j=1}^{N} \text{sim}(Q_i, K_j) V_j}{\sum_{j=1}^{N} \text{sim}(Q_i, K_j)} \end{equation} Vi′=∑j=1Nsim(Qi,Kj)∑j=1Nsim(Qi,Kj)Vj

当将相似度函数替换为 sim ( q , k ) = exp ⁡ ( q ⊤ k D ) \text{sim}(q, k) = \exp\left(\frac{q^\top k}{\sqrt{D}}\right) sim(q,k)=exp(D q⊤k) 时，公式 ( 3 ) (3) (3) 等价于公式 ( 2 ) (2) (2)。

论文中提到矩阵的下标 i i i 表示取该矩阵第 i i i 行的行向量，但当公式中写 Q i 、 K i Q_i、K_i Qi、Ki 作为向量时，是按照常用的列向量来理解的，因此会看到矩阵的 Q K ⊤ QK^{\top} QK⊤ 和向量的 q ⊤ k q^{\top} k q⊤k、 ϕ ( Q i ) ⊤ ϕ ( K j ) \phi(Q_i)^{\top} \phi(K_j) ϕ(Qi)⊤ϕ(Kj) 两种转置形式。

二、线性化注意力

为了让公式 ( 3 ) (3) (3) 能够定义为一个注意力函数，唯一需要的约束是 sim ( ⋅ ) \text{sim}(\cdot) sim(⋅) 必须是非负的，这包括了所有的核函数 k ( x , y ) : R 2 × F → R + k(x,y):\mathbb{R^{2 \times F}} \to \mathbb{R}_+ k(x,y):R2×F→R+ 。

核函数 k ( x , y ) k(x,y) k(x,y) 的本质，是某个（可能是高维甚至无限维）特征空间中，特征映射 ϕ ( x ) , ϕ ( y ) \phi(x),\phi(y) ϕ(x),ϕ(y) 的内积： k ( x , y ) = ⟨ ϕ ( x ) , ϕ ( y ) ⟩ k(x,y)=\langle \phi(x),\phi(y) \rangle k(x,y)=⟨ϕ(x),ϕ(y)⟩ 。

给定一个具有特征表示 ϕ ( x ) \phi(x) ϕ(x) 的核函数，我们可以将公式 ( 3 ) (3) (3) 改写为：
V i ′ = ∑ j = 1 N ϕ ( Q i ) ⊤ ϕ ( K j ) V j ∑ j = 1 N ϕ ( Q i ) ⊤ ϕ ( K j ) \begin{equation} V'i = \frac{\sum{j=1}^{N} \phi(Q_i)^{\top} \phi(K_j) V_j}{\sum_{j=1}^{N} \phi(Q_i)^{\top} \phi(K_j)} \end{equation} Vi′=∑j=1Nϕ(Qi)⊤ϕ(Kj)∑j=1Nϕ(Qi)⊤ϕ(Kj)Vj

根据矩阵乘法的结合律，可进一步写为：
V i ′ = ϕ ( Q i ) ⊤ ∑ j = 1 N ϕ ( K j ) V j ⊤ ϕ ( Q i ) ⊤ ∑ j = 1 N ϕ ( K j ) \begin{equation} V'i = \frac{\phi(Q_i)^{\top} \sum{j=1}^{N} \phi(K_j) V_j^{\top}}{\phi(Q_i)^{\top} \sum_{j=1}^{N} \phi(K_j)} \end{equation} Vi′=ϕ(Qi)⊤∑j=1Nϕ(Kj)ϕ(Qi)⊤∑j=1Nϕ(Kj)Vj⊤

分子写为如下的矩阵形式更容易理解：
( ϕ ( Q ) ϕ ( K ) ⊤ ) V = ϕ ( Q ) ( ϕ ( K ) ⊤ V ) \begin{equation} \left(\phi(Q) \phi(K)^{\top}\right) V = \phi(Q) \left(\phi(K)^{\top} V\right) \end{equation} (ϕ(Q)ϕ(K)⊤)V=ϕ(Q)(ϕ(K)⊤V)

其中，特征映射 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅) 是逐行应用于矩阵 Q Q Q 和 K K K 的。

从公式 ( 2 ) (2) (2) 可以看出，softmax 注意力的计算和内存复杂度随序列长度 N N N 呈 O ( N 2 ) O(N^2) O(N2) 的规模增长。相比之下，线性注意力 ( 5 ) (5) (5) 具有 O ( N ) O(N) O(N) 的计算和内存复杂度，因为我们只需一次性计算 ∑ j = 1 N ϕ ( K j ) V j ⊤ \sum_{j=1}^{N} \phi(K_j) V_j^{\top} ∑j=1Nϕ(Kj)Vj⊤ 和 ∑ j = 1 N ϕ ( K j ) \sum_{j=1}^{N} \phi(K_j) ∑j=1Nϕ(Kj)，然后对每个查询重复使用这些结果即可。

特征映射与计算成本

（1）对于 softmax 注意力，计算过程可以分为两个主要的矩阵乘法步骤：

计算注意力分数 ( Q K ⊤ QK^{\top} QK⊤)，矩阵 Q Q Q 的维度是 N × D N \times D N×D，矩阵 K ⊤ K^{\top} K⊤ 的维度是 D × N D \times N D×N，计算开销为： O ( N 2 D ) O(N^2 D) O(N2D)。
计算最终输出（ Attention × V \text{Attention} \times V Attention×V)，注意力矩阵（经过 softmax 后）维度是 N × N N \times N N×N，矩阵 V V V 的维度是 N × M N \times M N×M，计算开销为： O ( N 2 M ) O(N^2 M) O(N2M)。
从量级上可以简记为 O ( N 2 max ⁡ ( D , M ) ) O(N^2 \max(D, M)) O(N2max(D,M))。

（2）对于线性注意力：

首先将维度为 D D D 的原始向量通过特征映射函数 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅) 映射到新空间，维度记为 C C C。
计算顺序利用结合律发生了改变： ϕ ( Q ) ( ϕ ( K ) ⊤ V ) \phi(Q)(\phi(K)^{\top} V) ϕ(Q)(ϕ(K)⊤V) ，先计算 ϕ ( K ) ⊤ V \phi(K)^{\top} V ϕ(K)⊤V，得到 C × M C \times M C×M 的隐状态矩阵，计算开销为： O ( N C M ) O(NCM) O(NCM)，再用 ϕ ( Q ) \phi(Q) ϕ(Q) 乘以该矩阵，计算开销相同，为 O ( N C M ) O(NCM) O(NCM)。

（3）对于一个简单的二阶齐次多项式核，其定义为： k ( x , y ) = ( x ⊤ y ) 2 k(x, y) = (x^{\top} y)^2 k(x,y)=(x⊤y)2，其中 x , y ∈ R D x, y \in \mathbb{R}^D x,y∈RD 是 D D D 维向量。

为了找到显式的特征映射 ϕ ( x ) \phi(x) ϕ(x)，我们需要将上述标量乘积的平方展开。假设 x = [ x 1 , x 2 , ... , x D ] ⊤ x = [x_1, x_2, \dots, x_D]^{\top} x=[x1,x2,...,xD]⊤ 和 y = [ y 1 , y 2 , ... , y D ] ⊤ y = [y_1, y_2, \dots, y_D]^{\top} y=[y1,y2,...,yD]⊤：

点积展开： x ⊤ y = ∑ i = 1 D x i y i x^{\top} y = \sum_{i=1}^D x_i y_i x⊤y=∑i=1Dxiyi
平方展开： ( x ⊤ y ) 2 = ( ∑ i = 1 D x i y i ) ⋅ ( ∑ j = 1 D x j y j ) = ∑ i = 1 D ∑ j = 1 D ( x i x j ) ( y i y j ) (x^{\top} y)^2 = (\sum_{i=1}^D x_i y_i) \cdot (\sum_{j=1}^D x_j y_j) = \sum_{i=1}^D \sum_{j=1}^D (x_i x_j)(y_i y_j) (x⊤y)2=(∑i=1Dxiyi)⋅(∑j=1Dxjyj)=∑i=1D∑j=1D(xixj)(yiyj)
展开式中的每一项都是 ( x i x j ) (x_i x_j) (xixj) 与 ( y i y j ) (y_i y_j) (yiyj) 的乘积，它是 ϕ ( x ) \phi(x) ϕ(x) 的内积由于 i i i 可以取 1 1 1 到 D D D， j j j 也可以取 1 1 1 到 D D D，所有可能的组合坐标 ( i , j ) (i, j) (i,j) 共有 D × D = D 2 D \times D = D^2 D×D=D2 个，即此时特征空间的维度为 C = D 2 C=D^2 C=D2。
因此二阶多项式线性 Transformer 的复杂度即为 O ( N D 2 M ) O(ND^2M) O(ND2M) 。
此时模型在序列长度 N N N 远大于 D 2 D^2 D2 时（ N > D 2 N > D^2 N>D2）具有显著的计算优势。

线性注意力的核心在于寻找一个合适的特征映射函数 ϕ ( x ) \phi(x) ϕ(x)，然而，这里存在一个理论上的挑战：标准 softmax 注意力使用的是指数核（Exponential Kernel），它对应的特征映射 ϕ ( x ) \phi(x) ϕ(x) 是无穷维的，这意味着要精确线性化 Softmax 是不可行的。

为了处理论文实验中规模较小的序列，作者并未使用复杂的多项式核，而是采用了一种更简洁的特征映射：
ϕ ( x ) = elu ( x ) + 1 \begin{equation} \phi(x) = \text{elu}(x) + 1 \end{equation} ϕ(x)=elu(x)+1

这是为了确保相似度分数非负，elu (exponential linear unit) 激活函数表达如下：
elu ( x ) = { x if x > 0 α ( e x − 1 ) if x ≤ 0 \begin{equation} \text{elu}(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha(e^x - 1) & \text{if } x \le 0 \end{cases} \end{equation} elu(x)={xα(ex−1)if x>0if x≤0

其中 α \alpha α 通常取 1.0。这样的 ϕ ( x ) \phi(x) ϕ(x) 保证了 x x x 为负数时仍有梯度，且始终非负，在此定义下有 C = D C=D C=D。

三、因果掩码

Transformer 架构可以通过对注意力计算进行掩码处理，来高效训练自回归模型，使得第 i i i 个位置只能受到第 j j j 个位置的影响，当且仅当 j ≤ i j \le i j≤i。形式上，这种因果掩码对公式 ( 3 ) (3) (3) 的修改如下：
V i ′ = ∑ j = 1 i sim ( Q i , K j ) V j ∑ j = 1 i sim ( Q i , K j ) \begin{equation} V'i = \frac{\sum{j=1}^{\color{red}{i}} \text{sim}(Q_i, K_j) V_j}{\sum_{j=1}^{\color{red}{i}} \text{sim}(Q_i, K_j)} \end{equation} Vi′=∑j=1isim(Qi,Kj)∑j=1isim(Qi,Kj)Vj

进一步可以写为：
V i ′ = ϕ ( Q i ) ⊤ ∑ j = 1 i ϕ ( K j ) V j ⊤ ϕ ( Q i ) ⊤ ∑ j = 1 i ϕ ( K j ) \begin{equation} V'i = \frac{\phi(Q_i)^{\top} \sum{j=1}^{\color{red}{i}} \phi(K_j) V_j^{\top}}{\phi(Q_i)^{\top} \sum_{j=1}^{\color{red}{i}} \phi(K_j)}\end{equation} Vi′=ϕ(Qi)⊤∑j=1iϕ(Kj)ϕ(Qi)⊤∑j=1iϕ(Kj)Vj⊤

定义：
S i = ∑ j = 1 i ϕ ( K j ) V j ⊤ \begin{equation} S_i = \sum_{j=1}^{i} \phi(K_j) V_j^{\top} \end{equation} Si=j=1∑iϕ(Kj)Vj⊤

Z i = ∑ j = 1 i ϕ ( K j ) \begin{equation} Z_i = \sum_{j=1}^{i} \phi(K_j) \end{equation} Zi=j=1∑iϕ(Kj)

S i S_i Si 可以理解为注意力存储状态 ， Z i Z_i Zi 可以理解为归一化存储状态 。它们可以通过增量的方式进行更新，对于第 t t t 步的状态，有：
{ S t = S t − 1 + ϕ ( K t ) V t ⊤ , Z t = Z t − 1 + ϕ ( K t ) , \begin{equation} \begin{cases} S_t = S_{t-1} + \phi(K_t) V_t^{\top}, \\ Z_t = Z_{t-1} + \phi(K_t), \end{cases} \end{equation} {St=St−1+ϕ(Kt)Vt⊤,Zt=Zt−1+ϕ(Kt),

这意味着计算每个时间步的复杂度是常数级 的。公式 ( 10 ) (10) (10) 可以进一步写为：
V i ′ = ϕ ( Q i ) ⊤ S i ϕ ( Q i ) ⊤ Z i \begin{equation} V'_i = \frac{\phi(Q_i)^{\top} S_i}{\phi(Q_i)^{\top} Z_i} \end{equation} Vi′=ϕ(Qi)⊤Ziϕ(Qi)⊤Si

（一）梯度计算

本部分公式较多，重要节点的公式将通过方框框住，大部分内容来源于论文附录。

在任何深度学习框架中，对公式 ( 14 ) (14) (14) 的简单实现，是先前向，记录计算图/中间张量，然后再按图回传梯度。在这种实现下，框架为了能回传梯度，会把每一步的中间值 S i S_i Si 都缓存下来。

如前所述， D D D 是 query/key 的维度， M M M 是 value 的维度， N N N 是序列长度。缓存输入序列的 ϕ ( K ) \phi(K) ϕ(K)、 V V V，大小分别是 N × D N \times D N×D、 N × M N \times M N×M，如果每一步需缓存 S i S_i Si 矩阵，则需额外缓存的大小为 N × D × M N \times D \times M N×D×M，这会限制长序列和更深层模型的性能。

为了避免缓存全部的 S i S_i Si ，可以将梯度也改写为累计和（cumulative sums）的形式，从而使前向与反向中的因果线性注意力计算都具有线性时间和恒定缓存开销。

接下来，我们推导标量损失对公式 ( 10 ) (10) (10) 的梯度。其中，分母和整条分式的梯度直接交给 autograd，因为他们只涉及向量前缀和，内存压力小。重点只推导分子的梯度，因为分子中有 ∑ j = 1 i ϕ ( K j ) V j ⊤ \sum_{j=1}^{i} \phi(K_j) V_j^{\top} ∑j=1iϕ(Kj)Vj⊤，这正是我们需要解决的避免缓存多步 S i S_i Si 的地方。

首先简化符号，把 Q , K Q,K Q,K 直接当做已经过特征 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅) 映射的向量，因此分子（即未归一化输出）可以写成：
V ˉ i = Q i ⊤ ∑ j = 1 i K j V j ⊤ \begin{equation} \bar{V}i = Q_i^{\top} \sum{j=1}^{i} K_j V_j^{\top} \end{equation} Vˉi=Qi⊤j=1∑iKjVj⊤

因此为了计算 ∇ V ˉ L \nabla_{\bar{V}} \mathcal{L} ∇VˉL，我们需要计算 ∇ Q L \nabla_Q \mathcal{L} ∇QL、 ∇ K L \nabla_K \mathcal{L} ∇KL 和 ∇ V L \nabla_V \mathcal{L} ∇VL。我们首先把上式的某个分量（第 e e e 个 value 维度）写成标量形式 ：
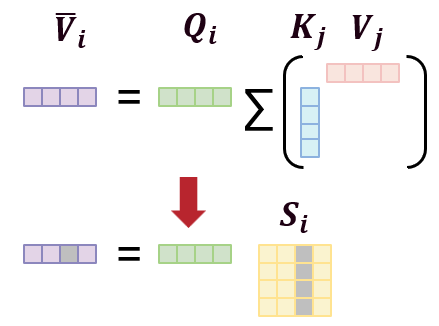
V ˉ i e = ∑ d = 1 D Q i d ∑ j = 1 i K j d V j e = ∑ d = 1 D ∑ j = 1 i Q i d K j d V j e \begin{equation} \boxed{\bar{V}{ie} = \sum{d=1}^{D} Q_{id} \sum_{j=1}^{i} K_{jd} V_{je} = \sum_{d=1}^{D} \sum_{j=1}^{i} Q_{id} K_{jd} V_{je}} \end{equation} Vˉie=d=1∑DQidj=1∑iKjdVje=d=1∑Dj=1∑iQidKjdVje

即如下图所示，灰色部分代表第 e e e 个维度的分量：

1. 对Q的梯度

为了对 Q Q Q 求梯度，可从对任意 Q l t Q_{lt} Qlt 求梯度开始。其中， l l l 是指第 l l l 个 token， t t t 是指第 t t t 维特征，由于 Q ∈ R N × D Q \in \mathbb{R}^{N \times D} Q∈RN×D，因此 Q l t Q_{lt} Qlt 就是矩阵 Q Q Q 的第 l l l 行第 t t t 列的元素。这里我们求的是标量损失 L \mathcal{L} L 对标量 Q l t Q_{lt} Qlt 的偏导， L \mathcal{L} L 不是直接依赖 Q l t Q_{lt} Qlt 的，它是通过中间量 V ˉ \bar{V} Vˉ 依赖的。对固定位置 l l l， V ˉ \bar{V} Vˉ 是一个 M M M 维向量，包含的元素有 V ˉ l 1 , ... , V ˉ l M \bar{V}{l1}, \dots, \bar{V}{lM} Vˉl1,...,VˉlM。因此要遍历每一个中间元素，根据链式法则，有：
∂ L ∂ Q l t = ∑ e = 1 M ∂ L ∂ V ˉ l e ∂ V ˉ l e ∂ Q l t \begin{equation} \frac{\partial \mathcal{L}}{\partial Q_{lt}} = \sum_{e=1}^{M} \frac{\partial \mathcal{L}}{\partial \bar{V}{le}} \frac{\partial \bar{V}{le}}{\partial Q_{lt}} \end{equation} ∂Qlt∂L=e=1∑M∂Vˉle∂L∂Qlt∂Vˉle

为什么上述链式法则只用对 e e e 从 1 ∼ M 1 \sim M 1∼M 求和，而不用考虑其他中间变量 V ˉ i e , ( i ≠ l ) \bar{V}{ie},(i \neq l) Vˉie,(i=l)？即为什么不对 i i i 求和？根据公式 ( 16 ) (16) (16)，当 i ≠ l i \neq l i=l 时， V ˉ i e \bar{V}{ie} Vˉie 里只会包含 Q i d Q_{id} Qid，不会包含 Q l t Q_{lt} Qlt，所以 ∂ V ˉ i e ∂ Q l t = 0 , ( i ≠ l ) \frac{\partial \bar{V}{ie}}{\partial Q{lt}}=0,(i \neq l) ∂Qlt∂Vˉie=0,(i=l)，因此整个链式法则里无需 ∑ i \sum_i ∑i，只保留 i = l i=l i=l 即可。这也是原文中所说的： Q l t Q_{lt} Qlt only affects V ˉ l \bar{V}_l Vˉl 。

现在继续计算 ∂ V ˉ l e ∂ Q l t \frac{\partial \bar{V}{le}}{\partial Q{lt}} ∂Qlt∂Vˉle，首先把 i = l i=l i=l 代入公式 ( 16 ) (16) (16) 中，可得：
V ˉ l e = ∑ d = 1 D ∑ j = 1 l Q l d K j d V j e \begin{equation} \bar{V}{le} = \sum{d=1}^{D} \sum_{j=1}^{l} Q_{ld} K_{jd} V_{je} \end{equation} Vˉle=d=1∑Dj=1∑lQldKjdVje

注意到当 ∂ Q l d ∂ Q l t = 1 \frac{\partial Q_{ld}}{\partial Q_{lt}}=1 ∂Qlt∂Qld=1，当且仅当 d = t d=t d=t 时，否则为 0。因此：
∂ V ˉ l e ∂ Q l t = ∑ d = 1 D ∑ j = 1 l ∂ ( Q l d K j d V j e ) ∂ Q l t = ∑ j = 1 l K j t V j e \begin{equation} \frac{\partial \bar{V}{le}}{\partial Q{lt}} = \sum_{d=1}^{D} \sum_{j=1}^{l} \frac{\partial (Q_{ld} K_{jd} V_{je})}{\partial Q_{lt}} = \sum_{j=1}^{l} K_{jt} V_{je} \end{equation} ∂Qlt∂Vˉle=d=1∑Dj=1∑l∂Qlt∂(QldKjdVje)=j=1∑lKjtVje

因此，对任意 Q l t Q_{lt} Qlt 求梯度有：
∂ L ∂ Q l t = ∑ e = 1 M ∂ L ∂ V ˉ l e ∂ V ˉ l e ∂ Q l t = ∑ e = 1 M ∂ L ∂ V ˉ l e ( ∑ j = 1 l K j t V j e ) \begin{equation} \boxed{\frac{\partial \mathcal{L}}{\partial Q_{lt}} = \sum_{e=1}^{M} \frac{\partial \mathcal{L}}{\partial \bar{V}{le}} \frac{\partial \bar{V}{le}}{\partial Q_{lt}} = \sum_{e=1}^{M} \frac{\partial \mathcal{L}}{\partial \bar{V}{le}} \left( \sum{j=1}^{l} K_{jt} V_{je} \right)} \end{equation} ∂Qlt∂L=e=1∑M∂Vˉle∂L∂Qlt∂Vˉle=e=1∑M∂Vˉle∂L(j=1∑lKjtVje)

下面，需要把元素级的上式进一步转换为矩阵表达，并表示出它和前缀矩阵 S l = ∑ j ≤ l K j V j ⊤ S_l = \sum_{j \le l} K_j V_j^{\top} Sl=∑j≤lKjVj⊤ 的关系。首先，引入一个上游梯度向量（维度为 M M M）：
g l ≜ ∇ V ˉ l L ∈ R M , ( g l ) e = ∂ L ∂ V ˉ l e \begin{equation} g_l \triangleq \nabla_{\bar{V}_l} \mathcal{L} \in \mathbb{R}^M, \quad (g_l)e = \frac{\partial \mathcal{L}}{\partial \bar{V}{le}} \end{equation} gl≜∇VˉlL∈RM,(gl)e=∂Vˉle∂L

可见该梯度向量的第 e e e 个分量就是元素级的 ∂ L ∂ V ˉ l e \frac{\partial \mathcal{L}}{\partial \bar{V}{le}} ∂Vˉle∂L。此外，引入前缀矩阵（维度为 D × M D \times M D×M）：
S l ≜ ∑ j = 1 l K j V j ⊤ ∈ R D × M \begin{equation} S_l \triangleq \sum{j=1}^{l} K_j V_j^\top \in \mathbb{R}^{D \times M} \end{equation} Sl≜j=1∑lKjVj⊤∈RD×M

它的第 t t t 行第 e e e 列是：
( S l ) t e = ∑ j = 1 l K j t V j e \begin{equation} (S_l){te} = \sum{j=1}^{l} K_{jt} V_{je} \end{equation} (Sl)te=j=1∑lKjtVje

那么公式 ( 20 ) (20) (20) 可以改写为：
∂ L ∂ Q l t = ∑ e = 1 M ( g l ) e ( S l ) t e = g l ⊤ ⋅ ( S l ) t ⊤ \begin{equation} \frac{\partial \mathcal{L}}{\partial Q_{lt}} = \sum_{e=1}^{M} (g_l)e (S_l){te} = g_l^{\top} \cdot (S_l)_t^{\top} \end{equation} ∂Qlt∂L=e=1∑M(gl)e(Sl)te=gl⊤⋅(Sl)t⊤

可见，它实际上是向量 g l g_l gl 与矩阵 S l S_l Sl 的第 t t t 个行向量的点积（按维度 e e e 求和）。现在我们想要的不是单个元素，而是整行向量的梯度：
∇ Q l L = [ ∂ L ∂ Q l 1 , ∂ L ∂ Q l 2 , ... , ∂ L ∂ Q l D ] ∈ R D \begin{equation} \nabla_{Q_l} \mathcal{L} = \left[ \frac{\partial \mathcal{L}}{\partial Q_{l1}}, \frac{\partial \mathcal{L}}{\partial Q_{l2}}, \ldots, \frac{\partial \mathcal{L}}{\partial Q_{lD}} \right] \in \mathbb{R}^D \end{equation} ∇QlL=[∂Ql1∂L,∂Ql2∂L,...,∂QlD∂L]∈RD

对每个 t t t，我们都可用公式 ( 24 ) (24) (24) 来计算，有：
∇ Q l L = [ g l ⊤ ( S l ) 1 ⊤ , g l ⊤ ( S l ) 2 ⊤ , ... , g l ⊤ ( S l ) D ⊤ ] = g l ⊤ S l ⊤ ∈ R D \begin{equation} \nabla_{Q_l} \mathcal{L} = \left[ g_l^{\top}(S_l)_1^{\top}, g_l^{\top}(S_l)_2^{\top}, \ldots , g_l^{\top}(S_l)_D^{\top} \right] = g_l^{\top}S_l^{\top} \in \mathbb{R}^D \end{equation} ∇QlL=[gl⊤(Sl)1⊤,gl⊤(Sl)2⊤,...,gl⊤(Sl)D⊤]=gl⊤Sl⊤∈RD

分别把 S l S_l Sl 和 g l g_l gl 写回 S l = ∑ j = 1 l K j V j ⊤ S_l = \sum_{j=1}^{l} K_j V_j^\top Sl=∑j=1lKjVj⊤ 和 ∇ V ˉ l L \nabla_{\bar{V}l} \mathcal{L} ∇VˉlL ，将下标替换为 i i i，最终得到：
∇ Q i L = ∇ V ˉ i L ( ∑ j = 1 l K j V j ⊤ ) ⊤ \begin{equation} \boxed{\nabla{Q_i} \mathcal{L} = \nabla_{\bar{V}i} \mathcal{L} \left( \sum{j=1}^{l} K_j V_j^\top \right)^\top} \end{equation} ∇QiL=∇VˉiL(j=1∑lKjVj⊤)⊤

2. 对K的梯度

同样从对某个具体的 key 元素 K l t K_{lt} Klt 开始计算梯度，但与公式 ( 17 ) (17) (17) 中的 Q l t Q_{lt} Qlt 只影响 V ˉ l \bar{V}l Vˉl 不同， K l K_l Kl 会影响所有后续位置的前缀和。为方便起见，将公式 ( 16 ) (16) (16) 重新列出：
V ˉ i e = ∑ d = 1 D ∑ j = 1 i Q i d K j d V j e \begin{equation} \bar{V}{ie} = \sum_{d=1}^{D} \sum_{j=1}^{i} Q_{id} K_{jd} V_{je} \end{equation} Vˉie=d=1∑Dj=1∑iQidKjdVje

可见在 V ˉ i \bar{V}i Vˉi 里有 ∑ j = 1 i \sum{j=1}^{i} ∑j=1i，因此：

只要 i ≥ l i \geq l i≥l，前缀 { 1 , ... , i } \{1, \ldots, i\} {1,...,i} 就包含 j = l j = l j=l，于是 V ˉ i \bar{V}i Vˉi 里就会出现 K l t K{lt} Klt
当 i < l i < l i<l 时，前缀不包含 l l l，所以 K l t K_{lt} Klt 根本不会影响 V ˉ i \bar{V}_i Vˉi

所以 K l t K_{lt} Klt 会影响所有 i = l , l + 1 , ... , N i = l, l+1, \ldots, N i=l,l+1,...,N 的输出 V ˉ i \bar{V}i Vˉi，根据链式法则，有：
∂ L ∂ K l t = ∑ e = 1 M ∑ i = 1 N ∂ L ∂ V ˉ i e ∂ V ˉ i e ∂ K l t \begin{equation} \frac{\partial \mathcal{L}}{\partial K{lt}} = \sum_{e=1}^{M} \sum_{i=1}^{N} \frac{\partial \mathcal{L}}{\partial \bar{V}{ie}} \frac{\partial \bar{V}{ie}}{\partial K_{lt}} \end{equation} ∂Klt∂L=e=1∑Mi=1∑N∂Vˉie∂L∂Klt∂Vˉie

由于当 i < l i < l i<l 时 ∂ V ˉ i e ∂ K l t = 0 \frac{\partial \bar{V}{ie}}{\partial K{lt}} = 0 ∂Klt∂Vˉie=0，因此进一步有：
∂ L ∂ K l t = ∑ e = 1 M ∑ i = l N ∂ L ∂ V ˉ i e ∂ V ˉ i e ∂ K l t \begin{equation} \frac{\partial \mathcal{L}}{\partial K_{lt}} = \sum_{e=1}^{M} \sum_{i=l}^{N} \frac{\partial \mathcal{L}}{\partial \bar{V}{ie}} \frac{\partial \bar{V}{ie}}{\partial K_{lt}} \end{equation} ∂Klt∂L=e=1∑Mi=l∑N∂Vˉie∂L∂Klt∂Vˉie

现在算核心项 ∂ V ˉ i e ∂ K l t \frac{\partial \bar{V}{ie}}{\partial K{lt}} ∂Klt∂Vˉie，从公式 ( 16 ) (16) (16) 中对 K l t K_{lt} Klt 求偏导，只有当索引满足 j = l j = l j=l 且 d = t d = t d=t 时，项中才会出现 K l t K_{lt} Klt，所以：
∂ V ˉ i e ∂ K l t = ∑ d = 1 D ∑ j = 1 i Q i d V j e ∂ K j d ∂ K l t \begin{equation} \frac{\partial \bar{V}{ie}}{\partial K{lt}} = \sum_{d=1}^{D} \sum_{j=1}^{i} Q_{id} V_{je} \frac{\partial K_{jd}}{\partial K_{lt}} \end{equation} ∂Klt∂Vˉie=d=1∑Dj=1∑iQidVje∂Klt∂Kjd

其中：
∂ K j d ∂ K l t = { 1 , j = l and d = t 0 , otherwise \begin{equation} \frac{\partial K_{jd}}{\partial K_{lt}} = \begin{cases} 1, & j = l \text{ and } d = t \\ 0, & \text{otherwise} \end{cases} \end{equation} ∂Klt∂Kjd={1,0,j=l and d=totherwise

因此只剩下一个命中项：
∂ V ˉ i e ∂ K l t = Q i t V l e ( i ≥ l ) . \begin{equation} \frac{\partial \bar{V}{ie}}{\partial K{lt}} = Q_{it} V_{le} \quad (i \geq l). \end{equation} ∂Klt∂Vˉie=QitVle(i≥l).

把它代回链式法则，就得到：
∂ L ∂ K l t = ∑ e = 1 M ∑ i = l N ∂ L ∂ V ˉ i e ( Q i t V l e ) \begin{equation} \frac{\partial \mathcal{L}}{\partial K_{lt}} = \sum_{e=1}^{M} \sum_{i=l}^{N} \frac{\partial \mathcal{L}}{\partial \bar{V}{ie}} (Q{it} V_{le}) \end{equation} ∂Klt∂L=e=1∑Mi=l∑N∂Vˉie∂L(QitVle)

同样的，引入上游梯度向量（维度为 M M M）：
g i ≜ ∇ V ˉ i L ∈ R M , ( g i ) e = ∂ L ∂ V ˉ i e \begin{equation} g_i \triangleq \nabla_{\bar{V}_i} \mathcal{L} \in \mathbb{R}^M, \quad (g_i)e = \frac{\partial \mathcal{L}}{\partial \bar{V}{ie}} \end{equation} gi≜∇VˉiL∈RM,(gi)e=∂Vˉie∂L

则有：
∂ L ∂ K l t = ∑ e = 1 M ∑ i = l N ( g i ) e Q i t V l e \begin{equation} \frac{\partial \mathcal{L}}{\partial K_{lt}} = \sum_{e=1}^{M} \sum_{i=l}^{N} (g_i)e \, Q{it} \, V_{le} \end{equation} ∂Klt∂L=e=1∑Mi=l∑N(gi)eQitVle

首先把对 e e e 的求和视为一个点积，其中跟 e e e 有关的部分是：
∑ e = 1 M ( g i ) e V l e \begin{equation} \sum_{e=1}^{M} (g_i)e V{le} \end{equation} e=1∑M(gi)eVle

它是两个 M M M 维向量的点积：
g i ⊤ V l \begin{equation} g_i^\top V_l \end{equation} gi⊤Vl

因此进一步得到：
∂ L ∂ K l t = ∑ i = l N Q i t ( g i ⊤ V l ) \begin{equation} \frac{\partial \mathcal{L}}{\partial K_{lt}} = \sum_{i=l}^{N} Q_{it} \left( g_i^\top V_l \right) \end{equation} ∂Klt∂L=i=l∑NQit(gi⊤Vl)

同样的，我们需要的是整行梯度：
∇ K l L = [ ∂ L ∂ K l 1 , ∂ L ∂ K l 2 , ... , ∂ L ∂ K l D ] ∈ R D \begin{equation} \nabla_{K_l} \mathcal{L} = \left[ \frac{\partial \mathcal{L}}{\partial K_{l1}}, \frac{\partial \mathcal{L}}{\partial K_{l2}}, \ldots, \frac{\partial \mathcal{L}}{\partial K_{lD}} \right] \in \mathbb{R}^D \end{equation} ∇KlL=[∂Kl1∂L,∂Kl2∂L,...,∂KlD∂L]∈RD

将公式 ( 39 ) (39) (39) 代入后得到：
∇ K l L = ∑ i = l N Q i ( g i ⊤ V l ) \begin{equation} \nabla_{K_l} \mathcal{L} = \sum_{i=l}^{N} Q_i (g_i^\top V_l) \end{equation} ∇KlL=i=l∑NQi(gi⊤Vl)

其中 Q i ∈ R D Q_i \in \mathbb{R}^D Qi∈RD， g i ⊤ g_i^\top gi⊤ 是 1 × M 1 \times M 1×M 的行向量， g i ⊤ V l g_i^\top V_l gi⊤Vl 是标量，即右边是若干个 D D D 维向量的加权和，结果仍是 D D D 维向量。此外：
Q i ( g i ⊤ V l ) = ( Q i g i ⊤ ) V l \begin{equation} Q_i (g_i^\top V_l) = (Q_i g_i^\top) V_l \end{equation} Qi(gi⊤Vl)=(Qigi⊤)Vl

其中外积 Q i g i ⊤ Q_i g_i^\top Qigi⊤ 是一个 D × M D \times M D×M 的矩阵。于是有：
∑ i = l N Q i ( g i ⊤ V l ) = ∑ i = l N ( Q i g i ⊤ ) V l = ( ∑ i = l N Q i g i ⊤ ) V l \begin{equation} \sum_{i=l}^{N} Q_i (g_i^\top V_l) = \sum_{i=l}^{N} (Q_i g_i^\top) V_l = \left( \sum_{i=l}^{N} Q_i g_i^\top \right) V_l \end{equation} i=l∑NQi(gi⊤Vl)=i=l∑N(Qigi⊤)Vl=(i=l∑NQigi⊤)Vl

这里的变换相当于是把 V l V_l Vl 提取了出来。把下标从 l l l 改为 i i i，把求和索引从 i i i 改为 j j j 避免冲突，同时把 g j g_j gj 写回 ∇ V ˉ j L \nabla_{\bar{V}j} \mathcal{L} ∇VˉjL，最终得到：
∇ K i L = ( ∑ j = i N Q j ( ∇ V ˉ j L ) ⊤ ) V i \begin{equation} \boxed{\nabla{K_i} \mathcal{L} = \left( \sum_{j=i}^{N} Q_j (\nabla_{\bar{V}_j} \mathcal{L})^\top \right) V_i} \end{equation} ∇KiL=(j=i∑NQj(∇VˉjL)⊤)Vi

可以看到，关于 Q Q Q 和 K K K 的梯度累计和矩阵具有相同的大小 D × M D \times M D×M：

对 Q l Q_l Ql，梯度只来自相同位置 l l l，所以是前缀结构（ ∑ j = 1 i \sum_{j=1}^i ∑j=1i）
对 K i K_i Ki，它影响所有未来位置 j ≥ i j \geq i j≥i，所以是后缀结构（ ∑ j = i N \sum_{j=i}^N ∑j=iN）

3. 对V的梯度

与对 K K K 的推导类似，从 V l t V_{lt} Vlt 开始计算梯度。同样为方便起见，再次将公式 ( 16 ) (16) (16) 重新列出：
V ˉ i e = ∑ d = 1 D ∑ j = 1 i Q i d K j d V j e \begin{equation} \bar{V}{ie} = \sum{d=1}^{D} \sum_{j=1}^{i} Q_{id} K_{jd} V_{je} \end{equation} Vˉie=d=1∑Dj=1∑iQidKjdVje

相同的：

只要 i ≥ l i \geq l i≥l，前缀 { 1 , ... , i } \{1, \ldots, i\} {1,...,i} 就包含 j = l j = l j=l，于是 V ˉ i \bar{V}i Vˉi 里就会出现 V l t V{lt} Vlt
当 i < l i < l i<l 时，前缀不包含 l l l，所以 V l t V_{lt} Vlt 根本不会影响 V ˉ i \bar{V}_i Vˉi

因此链式法则是：
∂ L ∂ V l t = ∑ e = 1 M ∑ i = l N ∂ L ∂ V ˉ i e ∂ V ˉ i e ∂ V l t \begin{equation} \frac{\partial \mathcal{L}}{\partial V_{lt}} = \sum_{e=1}^{M} \sum_{i=l}^{N} \frac{\partial \mathcal{L}}{\partial \bar{V}{ie}} \frac{\partial \bar{V}{ie}}{\partial V_{lt}} \end{equation} ∂Vlt∂L=e=1∑Mi=l∑N∂Vˉie∂L∂Vlt∂Vˉie

可见， K l , V l K_l, V_l Kl,Vl 都会影响所有的未来位置 i ≥ l i \geq l i≥l。

下面计算 ∂ V ˉ i e ∂ V l t \frac{\partial \bar{V}{ie}}{\partial V{lt}} ∂Vlt∂Vˉie，从公式 ( 16 ) (16) (16) 中对 V l t V_{lt} Vlt 求偏导，只有当索引满足 j = l j = l j=l 且 e = t e = t e=t 时，项中才会出现 V l t V_{lt} Vlt，所以：
∂ V ˉ i e ∂ V l t = ∑ d = 1 D ∑ j = 1 i Q i d K j d ∂ V j e ∂ V l t \begin{equation} \frac{\partial \bar{V}{ie}}{\partial V{lt}} = \sum_{d=1}^{D} \sum_{j=1}^{i} Q_{id} K_{jd} \frac{\partial V_{je}}{\partial V_{lt}} \end{equation} ∂Vlt∂Vˉie=d=1∑Dj=1∑iQidKjd∂Vlt∂Vje

其中：
∂ V j e ∂ V l t = { 1 , j = l and e = t 0 , otherwise \begin{equation} \frac{\partial V_{je}}{\partial V_{lt}} = \begin{cases} 1, & j = l \text{ and } e = t \\ 0, & \text{otherwise} \end{cases} \end{equation} ∂Vlt∂Vje={1,0,j=l and e=totherwise

因此：
∂ V ˉ i e ∂ V l t = ( ∑ d = 1 D Q i d K l d ) = ( Q i ⊤ K l ) , ( i ≥ l ) \begin{equation} \frac{\partial \bar{V}{ie}}{\partial V{lt}} = \left( \sum_{d=1}^{D} Q_{id} K_{ld} \right) = (Q_i^\top K_l), \quad (i \geq l) \end{equation} ∂Vlt∂Vˉie=(d=1∑DQidKld)=(Qi⊤Kl),(i≥l)

把它代回链式法则，得到：
∂ L ∂ V l t = ∑ i = l N ∂ L ∂ V ˉ i t ( Q i ⊤ K l ) \begin{equation} \frac{\partial \mathcal{L}}{\partial V_{lt}} = \sum_{i=l}^{N} \frac{\partial \mathcal{L}}{\partial \bar{V}_{it}} (Q_i^\top K_l) \end{equation} ∂Vlt∂L=i=l∑N∂Vˉit∂L(Qi⊤Kl)

注意，这里在计算 ∂ V j e ∂ V l t \frac{\partial V_{je}}{\partial V_{lt}} ∂Vlt∂Vje 时，已经将 e e e 约束为了 t t t 。和前一样，定义上游梯度向量：
g i ≜ ∇ V ˉ i L ∈ R M , ( g i ) t = ∂ L ∂ V ˉ i t \begin{equation} g_i \triangleq \nabla_{\bar{V}_i} \mathcal{L} \in \mathbb{R}^M, \quad (g_i)t = \frac{\partial \mathcal{L}}{\partial \bar{V}{it}} \end{equation} gi≜∇VˉiL∈RM,(gi)t=∂Vˉit∂L

进而得到：
∂ L ∂ V l t = ∑ i = l N ( g i ) t ( Q i ⊤ K l ) \begin{equation} \frac{\partial \mathcal{L}}{\partial V_{lt}} = \sum_{i=l}^{N} (g_i)_t (Q_i^\top K_l) \end{equation} ∂Vlt∂L=i=l∑N(gi)t(Qi⊤Kl)

我们需要的是整行梯度：
∇ V l L = [ ∂ L ∂ V l 1 , ∂ L ∂ V l 2 , ... , ∂ L ∂ V l M ] ∈ R M \begin{equation} \nabla_{V_l} \mathcal{L} = \left[ \frac{\partial \mathcal{L}}{\partial V_{l1}}, \frac{\partial \mathcal{L}}{\partial V_{l2}}, \ldots, \frac{\partial \mathcal{L}}{\partial V_{lM}} \right] \in \mathbb{R}^M \end{equation} ∇VlL=[∂Vl1∂L,∂Vl2∂L,...,∂VlM∂L]∈RM

将公式 ( 52 ) (52) (52) 代入得到：
∇ V l L = ∑ i = l N g i ( Q i ⊤ K l ) \begin{equation} \nabla_{V_l} \mathcal{L} = \sum_{i=l}^{N} g_i (Q_i^\top K_l) \end{equation} ∇VlL=i=l∑Ngi(Qi⊤Kl)

类似的，为了提取出 K l K_l Kl，可以进一步写为：
∇ V l L = ∑ i = l N g i ( Q i ⊤ K l ) = ∑ i = l N ( g i Q i ⊤ ) K l = ( ∑ i = l N ( Q i g i ⊤ ) ⊤ ) K l \begin{equation} \nabla_{V_l} \mathcal{L} = \sum_{i=l}^{N} g_i (Q_i^\top K_l) = \sum_{i=l}^{N} (g_i Q_i^\top) K_l = \left( \sum_{i=l}^{N} (Q_i g_i^\top)^\top \right) K_l \end{equation} ∇VlL=i=l∑Ngi(Qi⊤Kl)=i=l∑N(giQi⊤)Kl=(i=l∑N(Qigi⊤)⊤)Kl

其中，外积 Q i g i ⊤ Q_i g_i^\top Qigi⊤ 是一个 D × M D \times M D×M 的矩阵。把下标从 l l l 改为 i i i，把求和索引从 i i i 改为 j j j 避免冲突，同时把 g j g_j gj 写回 ∇ V ˉ j L \nabla_{\bar{V}j} \mathcal{L} ∇VˉjL，最终得到：
∇ V i L = ( ∑ j = i N Q j ( ∇ V ˉ j L ) ⊤ ) ⊤ K i \begin{equation} \boxed{\nabla{V_i} \mathcal{L} = \left( \sum_{j=i}^{N} Q_j (\nabla_{\bar{V}_j} \mathcal{L})^\top \right)^\top K_i} \end{equation} ∇ViL=(j=i∑NQj(∇VˉjL)⊤)⊤Ki

4. 小节

最终，我们将之前为了简化，省略去 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅) 的表达恢复，得到最终计算的梯度如下：
∇ ϕ ( Q i ) L = ∇ V ˉ i L ( ∑ j = 1 i ϕ ( K j ) V j ⊤ ) ⊤ ∇ ϕ ( K i ) L = ( ∑ j = i N ϕ ( Q j ) ( ∇ V ˉ j L ) ⊤ ) V i ∇ V i L = ( ∑ j = i N ϕ ( Q j ) ( ∇ V ˉ j L ) ⊤ ) ⊤ ϕ ( K i ) \begin{align} \nabla_{\phi(Q_i)} \mathcal{L} &= \nabla_{\bar{V}i} \mathcal{L} \left( \sum{j=1}^{i} \phi(K_j) V_j^\top \right)^{\top} \\ \nabla_{\phi(K_i)} \mathcal{L} &= \left( \sum_{j=i}^{N} \phi(Q_j) (\nabla_{\bar{V}j} \mathcal{L})^\top \right) V_i \\ \nabla{V_i} \mathcal{L} &= \left( \sum_{j=i}^{N} \phi(Q_j) (\nabla_{\bar{V}_j} \mathcal{L})^\top \right)^{\top} \phi(K_i) \end{align} ∇ϕ(Qi)L∇ϕ(Ki)L∇ViL=∇VˉiL(j=1∑iϕ(Kj)Vj⊤)⊤=(j=i∑Nϕ(Qj)(∇VˉjL)⊤)Vi=(j=i∑Nϕ(Qj)(∇VˉjL)⊤)⊤ϕ(Ki)

其中，为了计算 ∇ ϕ ( Q i ) L \nabla_{\phi(Q_i)} \mathcal{L} ∇ϕ(Qi)L，只需维护一个前缀矩阵，为了计算 ∇ ϕ ( K i ) L \nabla_{\phi(K_i)} \mathcal{L} ∇ϕ(Ki)L 和 ∇ V i L \nabla_{V_i} \mathcal{L} ∇ViL，只需维护一个后缀矩阵（两个矩阵相同，只是差了一个转置），避免了简单实现中需缓存所有的中间 S i S_i Si。结合公式 ( 14 ) (14) (14)，最终可以同时在前向、反向中，都保持线性的计算时间和固定大小的缓存。前向和反向过程中，分子计算的伪代码如下所示：

（二）训练和推理

在训练自回归 Transformer 模型时，完整的真实序列是可以获取的，这使得公式 ( 1 ) (1) (1) 中的 f l ( ⋅ ) f_l(\cdot) fl(⋅) 和注意力计算都能够实现分层并行。因此，Transformer 模型的训练效率比 RNN 更高。另一方面，在推理过程中，时间步 i i i 的输出会成为时间步 i + 1 i+1 i+1 的输入，这使得自回归模型无法进行并行化处理。此外，Transformer 模型每个时间步的成本并非固定不变的，而是与当前序列长度的平方成正比。

本文提出的线性 Transformer 兼具两者的优势。在训练方面，计算可以并行化，并充分利用GPU或其他加速器。在推理方面，每步预测的时间成本和内存成本都是恒定的。这意味着我们可以简单的将 ϕ ( K ) V ⊤ \phi(K)V^{\top} ϕ(K)V⊤ 存储为内部状态，并像 RNN 一样在每个时间步更新它，这使得推理速度比其他 Transformer 模型快数千倍。

四、Transformers are RNNs

通常，Transformer 模型被视为与 RNN 是两种根本不同的方法。但通过上面的讨论可知，任何带因果掩码的 Transformer 层可以表示为：给定输入，修改内部状态后再预测输出的模型，即 RNN。

通过如下的等式，我们将公式 ( 1 ) (1) (1) 中的 Transformer 层形式化为一个 RNN。由此得到的 RNN 具有两个隐藏状态，即 attention memory s s s 和 normalizer memory z z z 。我们使用下标来表示循环中的时间步：
s 0 = 0 z 0 = 0 s i = s i − 1 + ϕ ( x i W K ) ( x i W V ) ⊤ z i = z i − 1 + ϕ ( x i W K ) y i = f l ( ϕ ( x i W Q ) ⊤ s i ϕ ( x i W Q ) ⊤ z i + x i ) \begin{align} s_0 &= 0 \\ z_0 &= 0 \\ s_i &= s_{i-1} + \phi(x_i W_K) (x_i W_V)^\top \\ z_i &= z_{i-1} + \phi(x_i W_K) \\ y_i &= f_l \left( \frac{\phi(x_i W_Q)^\top s_i}{\phi(x_i W_Q)^\top z_i} + x_i \right) \end{align} s0z0siziyi=0=0=si−1+ϕ(xiWK)(xiWV)⊤=zi−1+ϕ(xiWK)=fl(ϕ(xiWQ)⊤ziϕ(xiWQ)⊤si+xi)

在上述等式中，对特征函数没有施加任何约束，理论上它可以表示任何 Transformer 模型，包括使用 softmax 注意力的模型。这些公式揭示了 Transformer 和 RNN 之间的关系，是我们更好的理解信息存储与检索的过程。

原文代码链接：https://linear-transformers.com ，其中公式 ( 57 ) (57) (57) - ( 59 ) (59) (59) 大约是通过 200 行 CUDA 代码实现的。

五、总结

文章的实验部分省略。本文提出了线性 Transformer 模型，大幅降低原始 Transformer 的内存与计算成本，利用矩阵乘积结合律使自注意力的时间和内存随序列长度呈线性增长，且在因果掩码下仍保持线性渐近复杂度。