
个人主页:
wengqidaifeng
✨ 永远在路上,永远向前走
文章目录
- 前言:数据结构的起点
- [一. 栈](#一. 栈)
-
- [1.1 栈的概念及结构](#1.1 栈的概念及结构)
- [二. 栈的实现](#二. 栈的实现)
-
- [1.1 栈的不同实现形式](#1.1 栈的不同实现形式)
- [1.2 数组实现:简洁而高效的经典方案](#1.2 数组实现:简洁而高效的经典方案)
-
- [1.2.1 核心数据结构设计](#1.2.1 核心数据结构设计)
- [1.2.2 初始化栈](#1.2.2 初始化栈)
- [1.2.3 核心操作实现](#1.2.3 核心操作实现)
- [1.2.4 完整工作流程示例](#1.2.4 完整工作流程示例)
- [1.3 数组实现栈的五大优势](#1.3 数组实现栈的五大优势)
- [1.4 数组实现栈的四大局限](#1.4 数组实现栈的四大局限)
- 对比表
- [2.1 链表实现:灵活优雅的动态方案](#2.1 链表实现:灵活优雅的动态方案)
-
- [1. 核心节点设计](#1. 核心节点设计)
- [2. 初始化栈](#2. 初始化栈)
- [3. 核心操作实现](#3. 核心操作实现)
-
- [入栈操作(Push) - 头插法](#入栈操作(Push) - 头插法)
- 出栈操作(Pop)
- 查看栈顶(Peek)
- 判断栈状态
- [4. 完整工作流程示例](#4. 完整工作流程示例)
- [2.2 链表实现栈的六大优势](#2.2 链表实现栈的六大优势)
-
- [1. **动态内存管理**](#1. 动态内存管理)
- [2. **无容量限制**](#2. 无容量限制)
- [3. **高效的插入删除**](#3. 高效的插入删除)
- [4. **空间利用率高**](#4. 空间利用率高)
- [5. **灵活的扩展性**](#5. 灵活的扩展性)
- [2.3 链表实现栈的五大局限](#2.3 链表实现栈的五大局限)
-
- [1. **内存开销较大**](#1. 内存开销较大)
- [2. **缓存不友好**](#2. 缓存不友好)
- [3. **内存分配开销**](#3. 内存分配开销)
- [4. **内存泄漏风险**](#4. 内存泄漏风险)
- [5. **代码复杂度增加**](#5. 代码复杂度增加)
- [2.4 选择链表实现的适用场景](#2.4 选择链表实现的适用场景)
- 总结
前言:数据结构的起点
在计算机科学这个庞大的知识体系中,数据结构犹如建筑的基石。当我们谈论数据结构时,栈(Stack)无疑是其中最经典、最优雅的概念之一。它简洁、直观,却蕴含着深刻的计算思想,贯穿于从底层硬件到高级软件开发的每一个层面。
栈的概念并非计算机科学家们的凭空创造,它源自我们日常生活中司空见惯的现象------餐厅里叠放的餐盘、书桌上堆叠的书籍、行李箱中层层叠放的衣服。这种"后进先出"的组织方式如此自然,以至于当我们将其抽象为计算模型时,几乎立刻能感受到它的力量和美感。
栈的历史溯源
从数学到计算机
栈的概念最早可以追溯到20世纪50年代。德国计算机科学家克劳斯·山姆尔森和弗里德里希·L·鲍尔在研究ALGOL 60语言的编译问题时,首次提出了"栈"这个术语。他们发现,在解析嵌套的算术表达式时,需要一个数据结构来保存中间结果和操作顺序,而这种需求正好对应着现实中的堆叠模型。
"栈"这个名称本身就很形象------它来自英文"stack",意为"堆叠",恰如其分地描述了数据的组织方式:就像叠盘子一样,你只能从最上面放入或取出。
硬件与栈的共生
有趣的是,栈的概念很快就从软件领域延伸到了硬件设计。1964年发布的Burroughs B5000计算机是第一台直接将栈支持集成到硬件架构中的商用计算机。这台机器的设计者认识到,许多编程问题------特别是子程序调用和中断处理------都能通过栈得到优雅的解决。
为什么栈如此重要?
计算本质的体现
栈的重要性首先体现在它反映了计算的本质特性。计算机程序执行时,函数调用、表达式求值、控制流程管理都天然地遵循着"后进先出"的原则。当你调用一个函数时,系统需要记住返回的位置;当这个函数又调用其他函数时,新的返回地址被压在旧的上面;当函数执行完毕,它从栈顶弹出,程序回到之前的执行点。
这种嵌套式的执行流程,正是栈的完美应用场景。正如计算机科学先驱高德纳所说:"栈是计算过程最基本的结构之一,它体现了计算的递归本质。"
抽象的力量
栈向我们展示了抽象的力量。通过定义简单的两个操作------入栈(push)和出栈(pop)------我们创造了一个可以解决无数复杂问题的工具。这种接口的简洁性与其能力的强大性形成了鲜明对比,这正是优秀设计的标志。
在本博客中,我们将深入探索栈的每一个方面:
- 栈的基本概念与ADT - 从抽象数据类型的角度理解栈
- 栈的实现艺术 - 数组实现与链表实现的对比与分析
- 栈的经典应用 - 从括号匹配到函数调用栈
- 递归与栈的深层联系 - 如何用栈理解递归的本质
- 栈在算法中的应用 - 深度优先搜索、回溯算法等
- 系统栈与调用约定 - 看看计算机底层如何使用栈
在随后的"下册"中,我们将探讨栈的姊妹结构------队列,分析它与栈的异同,以及它们如何共同构成了控制流和数据流管理的基石。
当我们开始这次栈的探索之旅时,不妨带着这样的思考:在纷繁复杂的计算问题中,哪些模式本质上就是"栈"的模式?我们生活中的哪些场景也遵循着"后进先出"的规律?
准备好了吗?让我们开始这场从餐厅餐盘到计算机内存的奇妙旅程,一起探索栈这个简单而又深奥的结构如何支撑起整个计算世界的基础。
一. 栈
1.1 栈的概念及结构
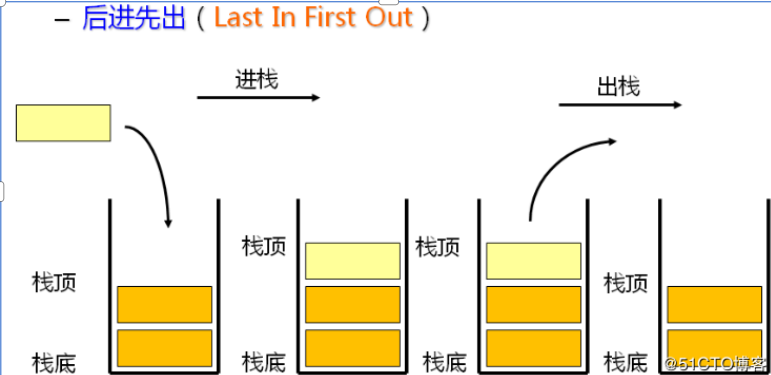
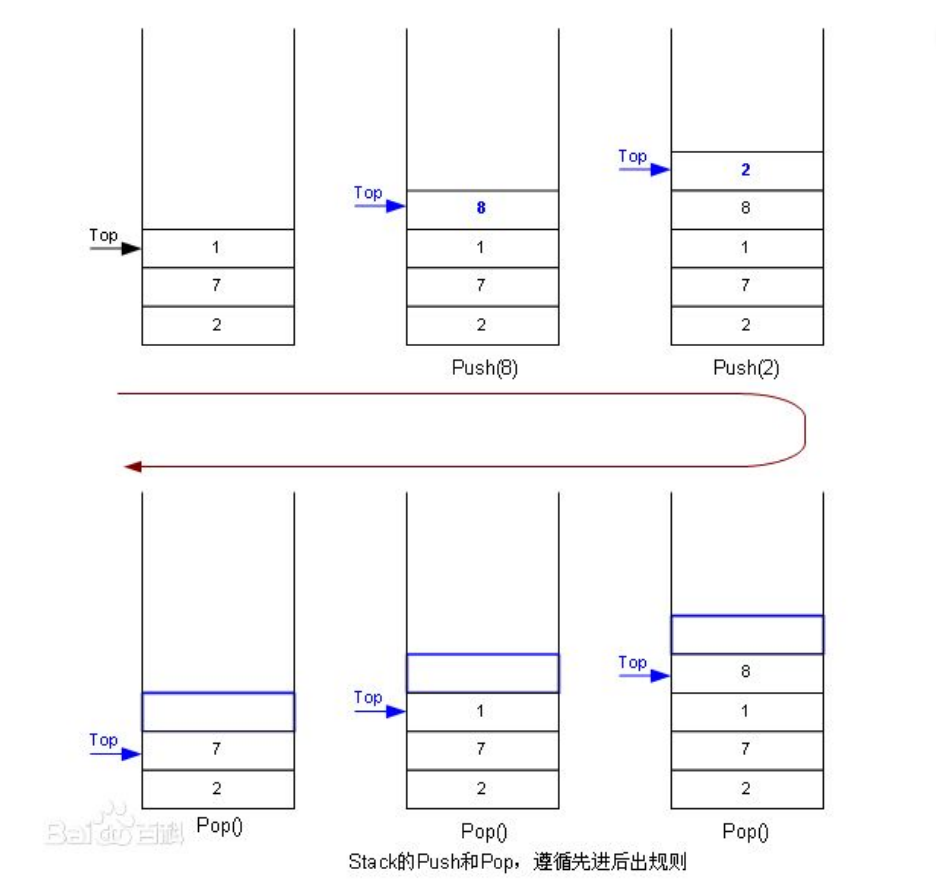
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。 栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈:栈的删除操作叫做出栈。出数据也在栈顶。
二. 栈的实现
1.1 栈的不同实现形式
栈的实现一般可以使用数组或者链表实现,相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小。
1.2 数组实现:简洁而高效的经典方案

1.2.1 核心数据结构设计
c
#define MAX_SIZE 100 // 栈的最大容量
typedef struct {
int data[MAX_SIZE]; // 存储栈元素的数组
int top; // 栈顶指针,指向当前栈顶位置
} ArrayStack;1.2.2 初始化栈
c
void initStack(ArrayStack *stack) {
stack->top = -1; // -1表示栈为空
// 可选:初始化数组元素为0
memset(stack->data, 0, sizeof(stack->data));
}1.2.3 核心操作实现
入栈操作(Push)
c
int push(ArrayStack *stack, int value) {
if (stack->top == MAX_SIZE - 1) {
printf("栈已满!\n");
return 0; // 失败
}
stack->data[++(stack->top)] = value; // 栈顶指针上移并存入数据
return 1; // 成功
}出栈操作(Pop)
c
int pop(ArrayStack *stack, int *value) {
if (stack->top == -1) {
printf("栈为空!\n");
return 0; // 失败
}
*value = stack->data[(stack->top)--]; // 取出数据后栈顶指针下移
return 1; // 成功
}查看栈顶(Peek)
c
int peek(ArrayStack *stack, int *value) {
if (stack->top == -1) {
return 0; // 失败
}
*value = stack->data[stack->top];
return 1; // 成功
}判断栈状态
c
int isEmpty(ArrayStack *stack) {
return stack->top == -1;
}
int isFull(ArrayStack *stack) {
return stack->top == MAX_SIZE - 1;
}1.2.4 完整工作流程示例
初始化: top = -1, data = [_, _, _, ...]
push(10): top = 0, data[0] = 10
push(20): top = 1, data[1] = 20
push(30): top = 2, data[2] = 30
当前栈: [10, 20, 30] // 索引0为栈底,索引2为栈顶
peek(): 返回30 (不改变栈)
pop(): 返回30, top = 1
pop(): 返回20, top = 0
pop(): 返回10, top = -1 (栈空)1.3 数组实现栈的五大优势
1.内存访问高效
- 连续内存布局,CPU缓存友好
- 随机访问特性,定位栈顶元素时间复杂度O(1)
- 无指针开销,内存利用率高
2.实现简单直观
- 代码量少,逻辑清晰
- 调试和维护容易
- 适合教学和快速原型开发
3.性能卓越
操作 时间复杂度 空间复杂度
push() O(1) O(1)
pop() O(1) O(1)
peek() O(1) O(1)
isEmpty() O(1) O(1)4.空间局部性好
- 数据连续存储,减少缓存缺失
- 预分配内存,无动态分配开销
5.确定性内存占用
- 编译期确定最大空间
- 无内存碎片问题
- 适合内存受限的嵌入式系统
1.4 数组实现栈的四大局限
1.容量固定
c
// 硬编码的限制
#define MAX_SIZE 100 // 无法动态调整
// 可能的问题场景
for(int i = 0; i < 1000; i++) {
push(&stack, i); // 第101次push将失败
}2.空间浪费风险
情况1:过度分配
MAX_SIZE = 1000
实际最多使用:50个元素
空间浪费:95%
情况2:分配不足
MAX_SIZE = 50
实际需要:200个元素
程序崩溃或数据丢失3.不支持动态扩展
c
// 无法像动态数组那样自动扩容
// 需要手动实现重新分配逻辑
int* new_data = (int*)realloc(stack.data, 2*MAX_SIZE);
// 但这样会破坏栈的简洁性4.插入删除限制
- 只能在栈顶操作
- 无法在中间插入或删除(这是栈的特性,但数组实现强化了这种限制)
选择数组实现的适用场景
推荐使用数组栈的情况
- 栈大小可预测:如编译器中的符号表(通常有固定上限)
- 性能要求极高:游戏引擎、实时系统
- 内存受限环境:嵌入式系统、单片机
- 简单应用场景:教学示例、算法竞赛
- 栈操作模式简单:主要是push/pop,很少需要遍历
不建议使用数组栈的情况
- 栈大小变化大:网络数据包处理
- 需要频繁调整容量:文本编辑器undo/redo
- 内存要求灵活:通用库开发
- 栈深度不可预测:递归算法(可能深度很大)
对比表
| 特性 | 数组栈 | 链表栈 |
|---|---|---|
| 插入时间复杂度 | O(1) | O(1) |
| 删除时间复杂度 | O(1) | O(1) |
| 空间开销 | 固定预分配 | 每个节点额外指针 |
| 缓存友好性 | 优秀 | 一般 |
| 内存利用率 | 可能浪费 | 按需分配 |
| 实现复杂度 | 简单 | 中等 |
| 动态扩展 | 困难 | 容易 |
栈的数组实现不仅是一种技术方案,更是一种设计哲学的体现:通过约束获得效率,通过简化实现可靠。这种思想,正是优秀软件设计的核心所在。
2.1 链表实现:灵活优雅的动态方案
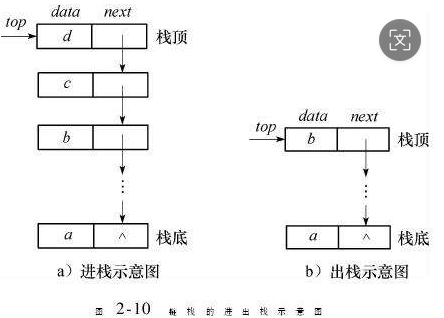
1. 核心节点设计
c
// 链表节点结构
typedef struct StackNode {
int data; // 存储数据
struct StackNode *next; // 指向下一个节点
} StackNode;
// 栈管理结构
typedef struct {
StackNode *top; // 栈顶指针
int size; // 当前栈大小(可选)
} LinkedStack;2. 初始化栈
c
void initLinkedStack(LinkedStack *stack) {
stack->top = NULL; // 空栈,top指向NULL
stack->size = 0; // 初始大小为0
}3. 核心操作实现
入栈操作(Push) - 头插法
c
int push(LinkedStack *stack, int value) {
// 创建新节点
StackNode *newNode = (StackNode*)malloc(sizeof(StackNode));
if (newNode == NULL) {
printf("内存分配失败!\n");
return 0; // 失败
}
// 初始化新节点
newNode->data = value;
newNode->next = stack->top; // 新节点指向原栈顶
// 更新栈顶指针
stack->top = newNode;
stack->size++;
return 1; // 成功
}出栈操作(Pop)
c
int pop(LinkedStack *stack, int *value) {
if (stack->top == NULL) {
printf("栈为空!\n");
return 0; // 失败
}
// 保存要弹出的节点
StackNode *temp = stack->top;
*value = temp->data; // 获取栈顶数据
// 更新栈顶指针
stack->top = temp->next;
stack->size--;
// 释放内存
free(temp);
return 1; // 成功
}查看栈顶(Peek)
c
int peek(LinkedStack *stack, int *value) {
if (stack->top == NULL) {
return 0; // 失败
}
*value = stack->top->data;
return 1; // 成功
}判断栈状态
c
int isEmpty(LinkedStack *stack) {
return stack->top == NULL; // 或者 return stack->size == 0;
}
// 链表栈理论上没有"满"的概念(除非内存耗尽)
int isFull(LinkedStack *stack) {
// 尝试分配一个新节点来测试
StackNode *test = (StackNode*)malloc(sizeof(StackNode));
if (test == NULL) {
free(test); // 虽然分配失败,但安全释放
return 1; // 内存耗尽,栈"满"
}
free(test);
return 0; // 内存充足
}4. 完整工作流程示例
初始化: top = NULL, size = 0
push(10): 创建节点A(data=10)
A->next = NULL
top = A
size = 1
push(20): 创建节点B(data=20)
B->next = A
top = B
size = 2
push(30): 创建节点C(data=30)
C->next = B
top = C
size = 3
当前栈结构: C → B → A → NULL
↑
top
peek(): 返回30 (C节点数据)
pop(): 返回30, 释放C, top指向B
pop(): 返回20, 释放B, top指向A
pop(): 返回10, 释放A, top = NULL (栈空)2.2 链表实现栈的六大优势
1. 动态内存管理
c
// 按需分配,无需预定义大小
while (有数据需要处理) {
push(&stack, data); // 自动分配节点
}
// 内存使用与实际需求完全匹配
// 栈大小只受系统内存限制2. 无容量限制
c
// 可以处理任意深度的递归或嵌套
// 例如:深度优先搜索、递归解析
void processDeepStructure() {
// 栈深度可能达到数千甚至更多
// 链表栈可以轻松应对
}3. 高效的插入删除
操作 时间复杂度 说明
push() O(1) 头部插入,只需修改指针
pop() O(1) 头部删除,直接释放4. 空间利用率高
数组栈:预分配100个位置,只用了10个 → 90%浪费
链表栈:用了10个节点 → 0%浪费(不考虑指针开销)5. 灵活的扩展性
c
// 容易添加额外功能
typedef struct EnhancedStackNode {
int data;
struct EnhancedStackNode *next;
struct EnhancedStackNode *prev; // 双向链表
time_t timestamp; // 额外信息
} EnhancedStackNode;2.3 链表实现栈的五大局限
1. 内存开销较大
c
// 每个节点需要额外存储指针
sizeof(StackNode) = sizeof(int) + sizeof(pointer)
// 在32位系统中:
// int: 4字节,指针: 4字节 → 8字节/节点
// 数组栈:每个元素只需4字节
// 内存开销增加约100%(不考虑数组预分配浪费)2. 缓存不友好
数组栈:连续内存,缓存命中率高
[10][20][30][40][50] ← 一次缓存加载多个元素
链表栈:内存分散,缓存命中率低
[10]→[20]→[30]→[40]→[50]
↑ ↑ ↑ ↑ ↑
不同内存区域,需要多次缓存加载3. 内存分配开销
c
// 每次push都需要malloc
push()操作包含:
1. malloc分配内存:系统调用,相对较慢
2. 初始化节点
3. 链接节点
// 对比数组栈的push:
1. 检查边界
2. 赋值4. 内存泄漏风险
c
// 必须手动释放所有节点
void destroyStack(LinkedStack *stack) {
int value;
while (pop(stack, &value)) {
// 逐一出栈释放
}
// 或者直接遍历释放
StackNode *current = stack->top;
while (current != NULL) {
StackNode *temp = current;
current = current->next;
free(temp);
}
stack->top = NULL;
stack->size = 0;
}5. 代码复杂度增加
c
// 需要处理指针操作
// 更多的边界条件检查
// 内存管理责任由程序员承担2.4 选择链表实现的适用场景
推荐使用链表栈的情况
-
栈大小不可预测
c// 递归深度未知的算法 int solvePuzzle(State state) { // 深度可能从1到10000不等 push(&stack, currentState); // ... } -
内存使用需要高度灵活
c// 内存受限但使用模式多变的系统 // 避免为最坏情况预分配大量内存 -
需要频繁调整容量
c// 文本编辑器undo/redo功能 // 用户可能进行数千次操作 // 但大多数时间只使用最近几十次 -
实现通用容器库
c// 库函数需要适应各种使用场景 // 无法假设用户的栈深度 -
栈元素大小可变
c// 存储不同大小的数据 typedef struct { void *data; // 任意类型数据 size_t dataSize; // 数据大小 struct Node *next; } GenericStackNode;
不建议使用链表栈的情况
-
对性能要求极高
- 实时系统、游戏引擎、高频交易
-
栈深度固定且已知
- 编译器符号表(通常有上限)
- 固定深度的状态机
-
内存极度受限
- 嵌入式系统、单片机
- 指针开销不可接受
-
需要频繁随机访问
- 虽然栈本身不支持,但数组实现更容易扩展
链表实现栈体现了动态与灵活的编程思想。它放弃了数组栈的内存连续性和缓存友好性,换来了无限制的扩展能力和精确的内存控制。
链表栈不仅是技术实现,更是一种设计态度的体现:宁愿付出一些性能代价,也要保证系统的灵活性和适应性。这种思想在构建可扩展、可维护的系统时尤为重要。
在掌握了数组和链表两种实现方式后,我们可以根据具体场景做出明智的选择。有时候,最佳方案可能是两者的结合------比如动态数组栈,或者带有节点池的链表栈。这正是软件工程的精髓:没有银弹,只有权衡。
总结
栈作为一种基础数据结构,遵循后进先出(LIFO)原则,仅允许在栈顶进行插入(入栈/push)和删除(出栈/pop)操作。其核心价值在于简洁、高效地处理具有嵌套或后到先服务特性的问题。
实现方式主要有两种:
- 数组实现:基于连续内存,通过栈顶指针管理。优点是访问高效、实现简单、缓存友好且内存占用确定;缺点是容量固定,可能造成空间浪费或溢出,缺乏动态扩展能力。
- 链表实现:基于动态节点链接,通过头插法维护。优点是容量动态、按需分配内存、无预设限制;缺点是内存开销较大(含指针)、缓存局部性差、内存分配与释放带来额外开销及复杂度。
选择建议:
- 数组栈适用于栈大小可预测、对性能要求高或内存受限的场景(如嵌入式系统、算法竞赛)。
- 链表栈适用于栈深度变化大、需要灵活内存管理或实现通用库的场景。
栈的设计体现了计算机科学中"通过约束获得效率"与"通过抽象管理复杂度"的核心思想,是理解递归、函数调用等计算模型的基础。实际应用中应结合具体需求在性能、内存与灵活性之间权衡选择。
最后,感谢各位大佬的观看!