标题
A lake water level prediction method based on data augmentation and Physics-Informed Neural Networks with imbalanced data
背景
作者
Lingjiang Lu , Tao Yan, Yongcan Chen
期刊来源
Journal of hydrology
DOI
10.1016/j.jhydrol.2025.134660
摘要
在过去三十年中,由于气候变化和用水需求增加,湖泊水位波动加剧,迫切需要准确有效的预测方法。然而,现有的基于深度学习的替代方法往往存在两大局限性:缺乏对超参数选择的物理指导,这增加了计算成本,以及极端水位样本的稀缺性,这导致数据集不平衡,准确性降低。为了解决这些局限性,本研究提出了一种新的物理信息神经网络(PINN)框架,该框架将数据增强与物理引导的超参数选择相结合。该框架采用边界水位时间序列作为输入,结合质量守恒约束,并应用基于聚类的增强方法来丰富极端事件样本。在中国南四湖下湖进行了适用性验证。使用均方根误差(RMSE)和纳什-萨特克利夫效率(NSE)进行评估表明,纳入物理约束可以显著提高预测精度,其性能甚至超过了经典的LSTM模型。物理引导下的超参数选择进一步提高了训练效率和准确性,在极端条件下,该增强方法将RMSE降低了69.1%。与现有的增强方法相比,该方法可将训练时间缩短63.35%,预测性能更好。最终代理模型的RMSE = 0.021 m,NSE > 0.94(相对于观测值),计算时间仅为传统水动力模型的2.42%。这些结果突出了该框架在可靠的现实世界水位预测及其向其他水文系统的可转移性方面的潜力。
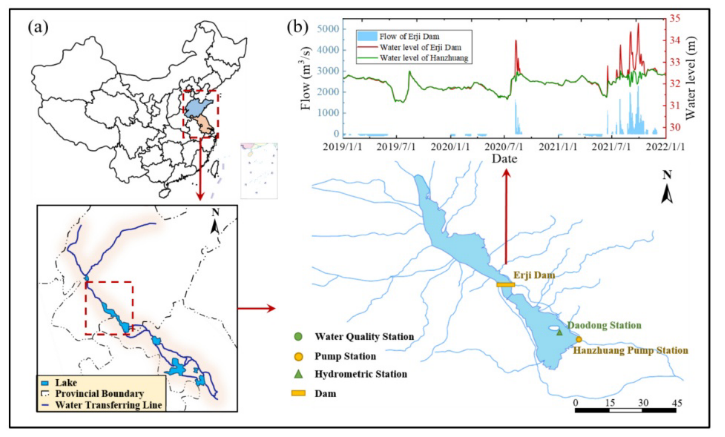
研究区域以及数据来源
南四湖是中国山东省最大的淡水湖,是南水北调东线工程(SNWDP-ER)的重要调节水库。20世纪60年代建成的二集大坝(EJ)将南四湖分为上湖和下湖。在干旱期,从12月到次年5月,下湖的水通过SNWDP-ER泵送到上湖。在汛期,从6月到11月,EJ闸门打开,将上湖多余的水释放到下湖。
算法
流动时间模式的识别
通过检测连续排放的序列来识别离散的流动事件,并使用零流量记录作为事件分离的标记。然后将流动时间模式的分类表述为多维空间中的聚类问题。将每个流量事件划分为k个等持续时间的区间,并计算每个区间中总水量的比例,以获得一组相对流量值q。这种转换允许将每个流量事件表示为k维空间中的一个点。随后根据合适的相似度指数进行聚类,本研究采用欧几里得距离L2,定义为:
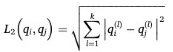
式中xi(l)和xj(l)分别为流动事件I和j第l段的水体积比。为了识别具有代表性的流动时间模式。
基于已识别的流动时间模式的特征,以及历史流动事件的持续时间和强度,选择适当的连续函数来随机生成合成流动事件,作为入口边界数据。这种方法通过补充代表性不足的流动模式和增强整体数据多样性,有助于缓解数据集中的不平衡。
利用MLP生成水位边界数据
在使用高保真水动力模型生成训练样本时,必须指定至少一个WL边界条件来模拟湖泊水动力。这些边界条件表现出内在的依赖关系和相互影响,这意味着合成样品的WL边界数据应根据其他边界对应的合成流动事件来确定,而不是通过简单的随机生成或组合。
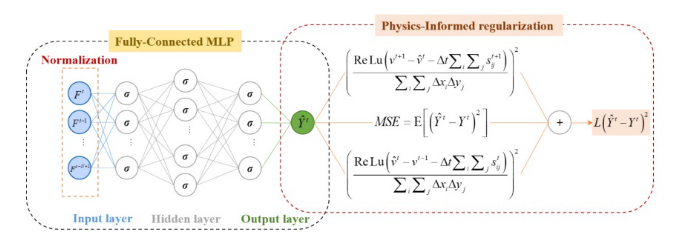
基于pinn的代理模型
基于pup的代理模型(PSM),该模型集成了质量守恒的物理定律,与纯粹的数据驱动模型相比,增强了可解释性和通用性。此外,他们还引入了一种新颖的网络架构,消除了对偏导数计算的需要,显著提高了模型的鲁棒性。在此框架的基础上,本研究利用PSM构建了一个用于水动力建模的神经网络。
结果分析
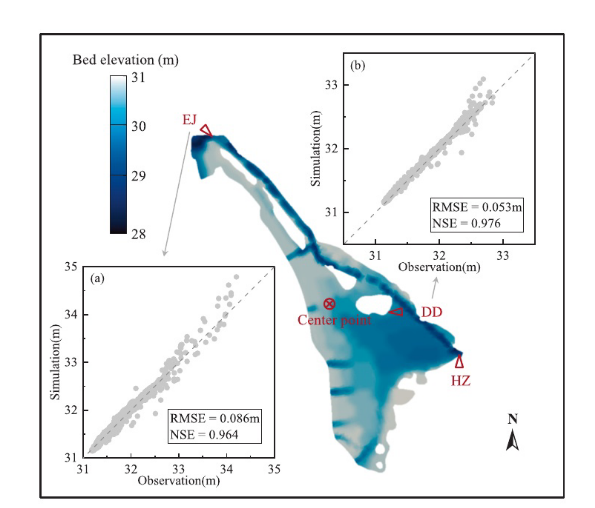
利用EJ和DD两个观测站的WL模拟对水动力模型进行了验证。两个观测站的RMSE值均低于0.1 m, NSE值均超过0.95,表明该模型在捕捉WL时空变化方面具有较高的精度。该模型在边界附近区域(如EJ和HZ)和湖内区域(如DD和中心域)表现良好,即使受到有限边界条件的约束。
首先,使用零流量记录将2019年至2021年的历史洪流量数据分割为9个不同的流量事件。将每个事件划分为10个等持续时间区间,计算每个区间的总流量占总流量的比例。然后将这些比例用作HCA的输入。基于聚类结果,将9个流事件分为三种时间模式。为了确保增强流数据集的多样性,为每个模式随机生成三个连续函数。然后根据洪水流量的历史范围(30-2290 m3/s)和持续时间(3-58天)对这些函数进行均匀采样和缩放。此外,引入随机噪声以增强变异性,从而产生总共9个合成流量过程。
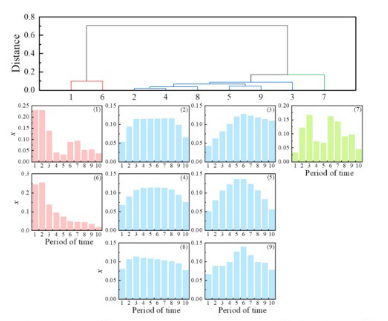
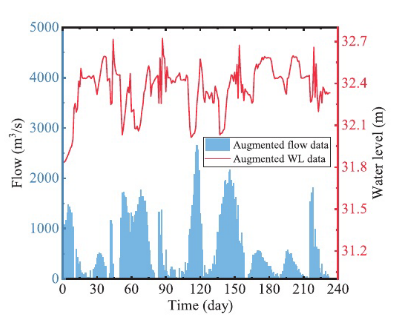
基于EJ处的增强流事件,采用MLP模型生成HZ处相应的WL变化。MLP模型使用历史数据进行训练,输入包括前一天的流量和WL数据,以及当天的流量数据。输出是当天的WL。
该框架为湖泊和水库的水位建模和模型优化提供了一个可重复且计算效率高的配方。物理信息的正则化和超参数规则为代理设计提供了一般指导,而基于聚类的增强策略广泛适用于极端事件代表性不足的不平衡数据集。尽管如此,该方法在研究湖泊的中心区域仍然表现出相对较大的预测误差。这种限制源于目前使用的质量守恒约束,它在每个网格单元内提供的局部指导不足。未来的工作将探索在损失函数中加入额外的物理约束,以进一步提高模型精度。