题目描述
天文学家经常研究星图,其中星星用平面上的点表示,每个星星都有笛卡尔坐标。定义一个星星的等级为:在该星星的左下方(包括正左和正下)的星星数量。天文学家想要知道星星等级的分布情况。
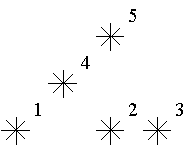
例如,如图所示的地图。星星5的等级等于3(由编号为1、2和4的三个星星组成)。星星2和4的等级为1。在这张地图上,有1颗等级为0的星星,2颗等级为1的星星,1颗等级为2的星星,和1颗等级为3的星星。
你要编写一个程序,统计给定地图上各等级星星的数量。
【问题描述】
天空中有一些星星,这些星星都在不同的位置,每个星星有个坐标。如果一个星星的左下方(包含正左和正下)有k颗星星,就说这颗星星是k级的。
【编程任务】
给定星星的位置,输出各级星星的数目。
给定n个点,定义每个点的等级是在该点左下方(含相等)的点的数目,试统计每个等级有多少个点。(n<=15000,0<=x,y<=32000)
输入格式
输入文件的第一行包含星星的数量N (1<=N<=15000)。接下来的N行描述星星的坐标(每行两个整数X和Y,用空格分隔,0<=X,Y<=32000)。每个点上只能有一颗星星。星星按照Y坐标升序排列。Y坐标相同的星星按照X坐标升序排列。
输出格式
输出应该包含N行,每行一个数字。第一行输出等级为 0 的星星数量,第二行输出等级为1的星星数量,依此类推,最后一行输出等级为N-1的星星数量。
样例
【样例输入】
5
1 1
5 1
7 1
3 3
5 5
【样例输出】
1
2
1
1
0
数据范围与提示
提示
这个问题的数据量很大,请使用scanf()而不是cin来读取数据以避免超时。
一些想法
这道题可以用树状数组做(树状数组具体看上一篇)。
因为这道题的 y 坐标是升序排序输入的,所以可以确保在处理当前星星时,上一个星星一定是在当前星星的下面或同一水平上的(横向),所以我们只用判断上一个星星是不是在当前星星的左边。所以这道题是一个一维树状数组。又因为树状数组是隐式判断,所以我们直接用前缀和查询就可以找到正确答案了。
定义两个数组,一个数组储存答案,一个树状数组储存前缀和。
先重置两个数组为 0。然后输入 n ,循环(从 0 到 n-1,因为输出等级是从等级 0 到等级 n-1),输入 x 坐标和 y 坐标(然后不用管 y 坐标),因为如果 x 是 0,lowbit(0)=0,会使下面两个自定义函数死循环,所以我们要进行偏移操作,将 x 加一(避免死循环)。然后找 x 星星的等级是多少,(查询 x 的前缀和),然后储存答案数组将这个等级数量加一,再将当前数(星星)加入树状数组,为后续星星查询提供数组,也就相当于标记这个位置有一个星星,然后这个星星的父节点也要随之增加。然后循环输出每个方案的数量。
函数部分,有三个自定义函数:lowbit 函数,查询 1~x 区间的和,修改 x (将 x 增加 y)。
lowbit 函数:用位运算找 x 二进制的最后一个 1 。树状数组的所有操作都基于 lowbit 实现区间划分。
查询函数:查询 1~x 区间的和,然后只要 x 大于 0(没有超出范围),然后将 x 不断减小(减自己的lowbit),跳转到前一个区间,将区间和增加上一个区间。(简单来说就是分解,将当前区间不断分解成多个小区间,然后将多个小区间累加,算出当前区间前缀和)。
修改函数:将第 x 个数增加 y ,因为前面的点有变化,所以包含这个点的在范围内的所有数都要跟着变化,因为父节点要随着子节点的变化而变化,所以每次增加自己的 lowbit ,也就是不断往后一个区间,直到达到边界,然后每一个区间都增加指定值。
注意:题目要求用 scanf() 读取数据避免超时。
AC代码
cpp
#include<bits/stdc++.h>
using namespace std;
int n,a[15005],c[32005];
int lowbit(int x){
return x&-x;
}
void zs(int x,int y){
for(;x<32005;x+=lowbit(x)){
c[x]+=y;
}
}
int sm(int x){
int sum=0;
for(;x>0;x-=lowbit(x)){
sum+=c[x];
}
return sum;
}
int main(){
memset(a,0,sizeof(a));
memset(c,0,sizeof(c));
scanf("%d", &n);
for(int i=0;i<n;i++){
int x,y;
scanf("%d %d", &x,&y);
int p=x+1;
int l=sm(p);
a[l]++;
zs(p,1);
}
for(int i=0;i<n;i++) printf("%d\n", a[i]);
return 0;
}