C++算法（4） - 技术栈

238.除了自身以外数组的乘积

首先拿到手没有思路时那就是暴力解法。

暴力法：对每个 i，用一个循环乘所有 j ≠ i 的元素 → O(n²)，超时。
优化思路：先算整个数组的乘积 total，然后 answer $i$ = total / nums $i$ → O(n)，但题目禁止使用除法（/），所以这条路被堵死。

然后重新观察发现，answer $i$ = (nums $0$ × ... × nums $i-1$ ) × (nums $i+1$ × ... × nums $n-1$ )

即：i 左侧所有元素的乘积 × i 右侧所有元素的乘积。

所以我们可以开两个数组：

left $i$ = nums $0$ × ... × nums $i-1$ （i 左侧乘积，left $0$ =1）
right $i$ = nums $i+1$ × ... × nums $n-1$ （i 右侧乘积，right $n-1$ =1）

过程：

cpp 复制代码

vector<int> left(n), right(n);
left[0] = 1;
for (int i = 1; i < n; ++i)
    left[i] = left[i-1] * nums[i-1];

right[n-1] = 1;
for (int i = n-2; i >= 0; --i)
    right[i] = right[i+1] * nums[i+1];

vector<int> answer(n);
for (int i = 0; i < n; ++i)
    answer[i] = left[i] * right[i];

在这个代码基础上继续优化。

观察到：这个过程只需要answer数组，left和right都是中间过程。所以我们可以先让answer存左侧乘积，然后再乘右侧乘积，得到最终答案。

代码

cpp 复制代码

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int n = nums.size();
        vector<int> answer(n, 1);
        for(int i = 1;i < n;i++){
            answer[i] = answer[i - 1] * nums[i - 1];
        }
        int r = 1;
        for(int i = n - 1;i >= 0;i--)
        {
            answer[i] *= r;
            r *= nums[i];
        }
        return answer;
    }
};

11.盛最多水的容器

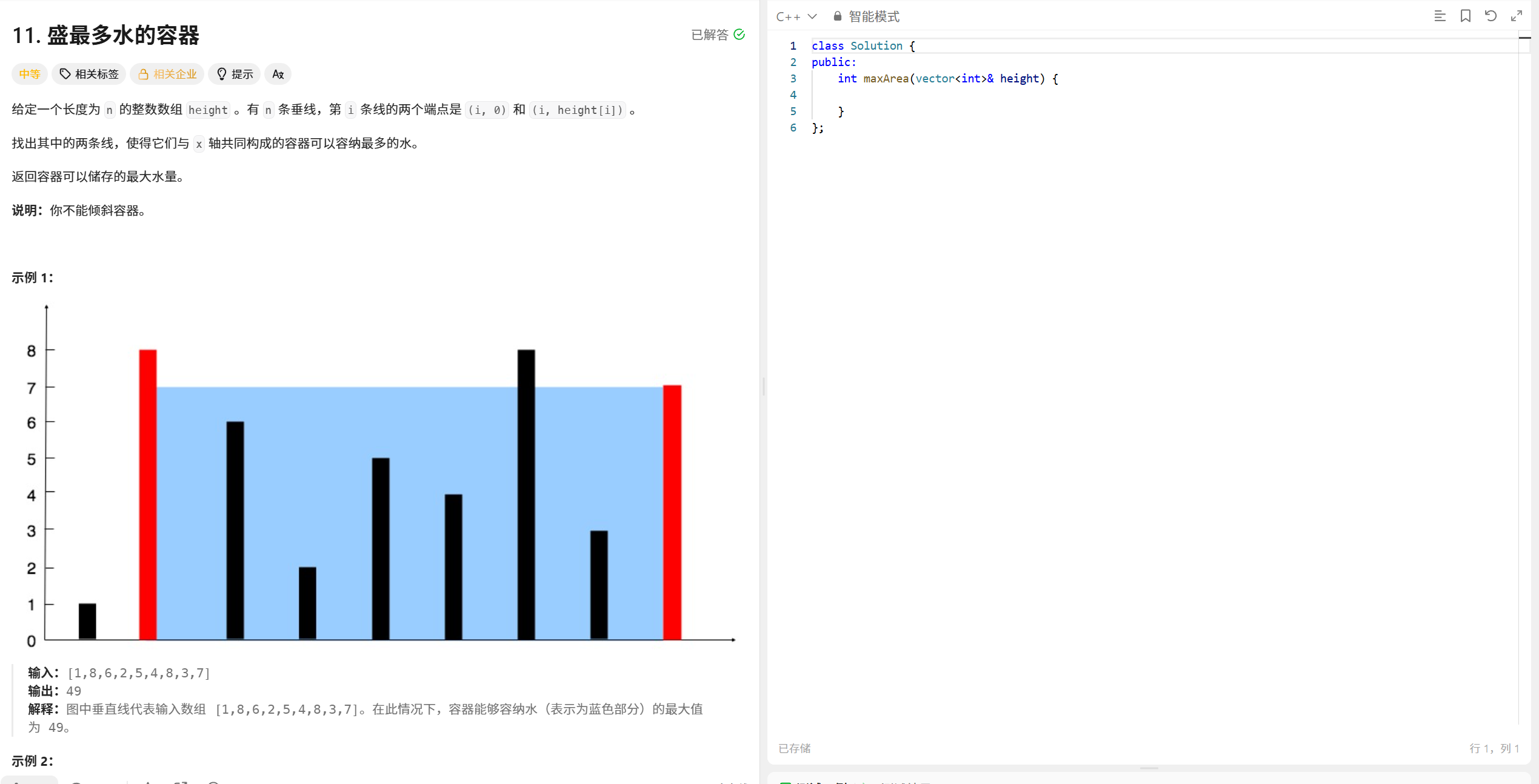
这个题，有点数学思路，首先我们得知道水量怎么计算。取两根柱子中最小的，然后乘柱子之间的下标差。

暴力的话就是两遍循环找最大。优化一下，那就用双指针。

一左一右，不断缩小遍历，得出最大的答案。

代码

cpp 复制代码

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0,right = height.size() - 1;
        int ans = -1;
        while(left < right)
        {
            int area = (right - left) * min(height[left],height[right]);
            ans = max(area,ans);
            if(height[left] > height[right]) right--;
            else left++;
        }
        return ans;
    }
};

560.和为K的子数组

依旧暴力解法就是两遍循环，然后不断加等。

cpp 复制代码

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int n = nums.size();
        int ans = 0;
        for(int i = 0;i < n;++i)
        {
            int sum = 0; // 每次外层循环重置sum
            for(int j = i;j < n;j++)
            {
                sum += nums[j];
                if(sum == k) ans++;
            }
        }
        return ans;
    }
};

但是会超时。所以优化一下。

利用前缀和和哈希表做。

代码

cpp 复制代码

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<long long, int> mp;  // key: 前缀和, value: 该前缀和出现次数
        mp[0] = 1;                         // 初始化：空前缀（从索引 0 开始前）的和为 0，出现 1 次
         
        long long prefix = 0;             // 当前前缀和
        int count = 0;                    // 答案：符合条件的子数组个数
        
        for (int num : nums) {
            prefix += num;                // 更新当前前缀和（到当前元素的累计和）
            
            // 查询：是否存在 earlier_prefix = prefix - k
            // 若存在，则说明从 earlier_prefix 之后到当前元素的子数组和为 k
            if (mp.count(prefix - k)) {
                count += mp[prefix - k];
            }
            
            // 更新当前前缀和的出现次数
            mp[prefix]++;
        }
        
        return count;
    }
};

525.连续数组

慢慢的做多了，遇到区间和，会想到使用前缀和。

这里的是0和1相加并且只有数字01，所以我们可以把0看作-1来做。

使用哈希表记录这个数最早出现的下标。

然后不断地遍历并记录下当前的前缀和以及下标

遇到相同的那么就更新最大长度

代码

cpp 复制代码

class Solution {
public:
    int findMaxLength(vector<int>& nums) {
        int n = nums.size();
        unordered_map<int, int> mp;  // 前缀和 → 最早出现的位置索引
        mp[0] = -1;                   // 初始化：空前缀和为 0，出现在索引 -1
        
        int prefix = 0;              // 当前前缀和
        int maxLen = 0;              // 最长长度
        
        for (int i = 0; i < n; ++i) {
            // 将 0 视为 -1，1 视为 +1
            prefix += (nums[i] == 0 ? -1 : 1);
            
            // 如果该前缀和之前出现过，计算长度并更新最大值
            if (mp.count(prefix)) {
                maxLen = max(maxLen, i - mp[prefix]);
            } else {
                // 只记录第一次出现的位置（保证子数组最长）
                mp[prefix] = i;
            }
        }
        
        return maxLen;
    }
};