Mamba3 深度剖析 - 03. 梯形离散化 (Trapezoidal Discretization)
核心摘要:本章深入探讨 Mamba-3 的核心创新之一------广义梯形离散化。接下来将从数值分析的角度揭示其精度优势,推导其数学形式,并论证其如何通过内建的"微型卷积"机制,从根本上替代了前代模型中的显式卷积层。
1. 动机:从一阶近似到二阶近似
在状态空间模型(SSM)中,核心挑战在于如何将连续时间的动态系统无损地映射到离散的时间步上。
1.1 连续系统定义
考虑标准的线性时变(LTV)系统:
h′(t)=A(t)h(t)+B(t)x(t) h'(t) = A(t)h(t) + B(t)x(t) h′(t)=A(t)h(t)+B(t)x(t)
y(t)=C(t)Th(t) y(t) = C(t)^T h(t) y(t)=C(t)Th(t)
- h(t)∈RNh(t) \in \mathbb{R}^Nh(t)∈RN:隐藏状态(Latent State),承载历史记忆。
- x(t)∈Rx(t) \in \mathbb{R}x(t)∈R:输入信号(Input Signal)。
- A(t),B(t)A(t), B(t)A(t),B(t):系统参数,随时间变化。
1.2 Mamba-2 的局限:欧拉法 (Euler Method)
Mamba-2 采用零阶保持(Zero-Order Hold, ZOH)原理,即假设在区间 [ti−1,ti][t_{i-1}, t_i][ti−1,ti] 内,输入 x(t)x(t)x(t) 是恒定不变的。这对应于数值分析中的欧拉法。
ht=eΔtAtht−1+ΔtBtxt h_t = e^{\Delta t A_t} h_{t-1} + \Delta t B_t x_t ht=eΔtAtht−1+ΔtBtxt
python
def selective_scan_euler_step(u_t, dt, A, B, h_prev):
"""
Mamba-2 官方参考实现逻辑片段 (简化展示)
体现 Euler / Zero-Order Hold (ZOH) 的局限性
"""
# 1. 计算衰减项 (Discretize A)
# 对应公式: alpha_t = exp(dt * A)
decay = torch.exp(dt * A)
# 2. 计算输入项 (Discretize B using Euler Method)
# ⚠️【局限性核心】:
# 欧拉法假设输入 u_t 在整个 dt 时间步长内保持不变 (Zero-Order Hold)。
# 因此,输入项仅由当前时刻的 u_t 决定,没有利用 u_{t-1} 的信息。
# 对应公式: input_term = dt * B * u_t
input_term = dt * (B * u_t)
# 3. 状态更新 (State Update)
# 递归公式: h_t = alpha_t * h_{t-1} + input_term
# 这里的 input_term 丢失了输入信号在 (t-1, t) 期间的二阶变化信息
h_t = decay * h_prev + input_term
return h_t❌ 精度瓶颈 :欧拉法仅提供一阶精度。
- 局部截断误差 (Local Truncation Error) :O(Δt2)O(\Delta t^2)O(Δt2)
- 全局累积误差 (Global Error) :O(Δt)O(\Delta t)O(Δt)
随着序列长度 LLL 的增加,这种线性累积的误差会削弱模型捕捉精细动态(如高频信号或快速变化趋势)的能力。
2. 核心突破:广义梯形法则 (Generalized Trapezoidal Rule)
Mamba-3 引入了广义梯形法则 来逼近状态更新积分。这是一种二阶精度的方法,通过利用区间两端的信息来提高估计的准确性。
2.1 几何直观与插图说明
请参考以下插图位置进行理解:
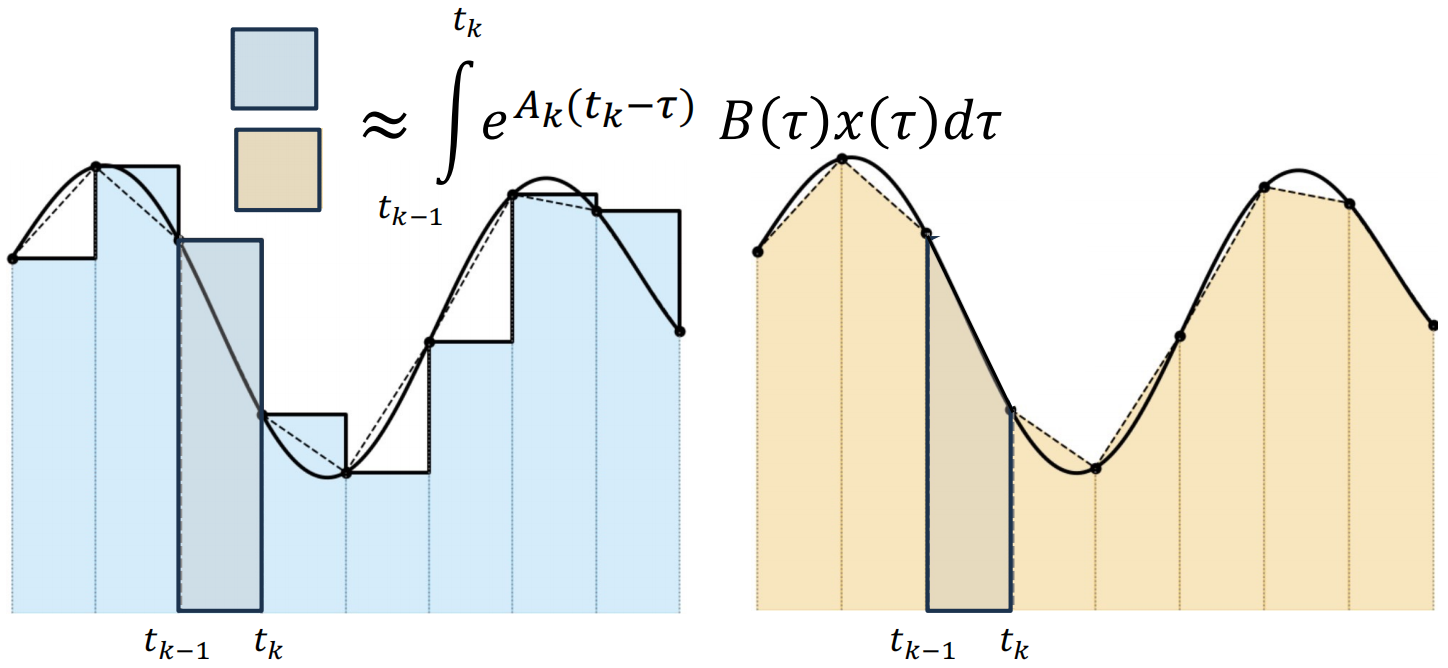
图1:数值积分方法的几何对比
- 来源 :论文 Figure 1 (Right Panel) 或网络搜索 "Euler vs Trapezoidal integration rule"。
- 说明 :
- 左图 (Euler) :用一个矩形面积近似曲线下的积分面积。矩形的高度由右端点 xtx_txt 决定。误差区域(矩形顶部与曲线之间的空隙)较大。
- 右图 (Trapezoidal) :用一个梯形面积近似。梯形的顶边连接了 xt−1x_{t-1}xt−1 和 xtx_txt。误差区域显著减小,更贴合曲线走势。
- 核心差异 :Mamba-3 不再"短视"地只看当前时刻 ttt,而是同时通过 t−1t-1t−1 和 ttt 时刻的加权来构建更新。
2.2 数学推导与公式详解
利用变常数公式(Variation of Constants),状态更新的积分项被近似为:
∫ti−1tieA(ti−τ)B(τ)x(τ)dτ≈(1−λt)ΔteΔtAtBt−1xt−1+λtΔtBtxt \int_{t_{i-1}}^{t_i} e^{A(t_i - \tau)} B(\tau) x(\tau) d\tau \approx (1 - \lambda_t)\Delta t e^{\Delta t A_t} B_{t-1} x_{t-1} + \lambda_t \Delta t B_t x_t ∫ti−1tieA(ti−τ)B(τ)x(τ)dτ≈(1−λt)ΔteΔtAtBt−1xt−1+λtΔtBtxt
由此导出 Mamba-3 的核心递归方程:
ht=αtht−1⏟记忆衰减+βtBt−1xt−1⏟历史输入贡献+γtBtxt⏟当前输入贡献 h_t = \underbrace{\alpha_t h_{t-1}}{\text{记忆衰减}} + \underbrace{\beta_t B{t-1} x_{t-1}}{\text{历史输入贡献}} + \underbrace{\gamma_t B_t x_t}{\text{当前输入贡献}} ht=记忆衰减 αtht−1+历史输入贡献 βtBt−1xt−1+当前输入贡献 γtBtxt
2.3 符号参数全解析 (Symbol & Parameter Reference)
| 符号 | 定义公式 | 维度 | 物理含义与解释 |
|---|---|---|---|
| hth_tht | - | RN\mathbb{R}^NRN | 隐藏状态。当前时刻系统的记忆快照。 |
| xtx_txt | - | R1\mathbb{R}^1R1 | 输入。当前时刻的离散输入信号。 |
| λt\lambda_tλt | [0,1][0, 1][0,1] (Learnable) | R1\mathbb{R}^1R1 | 混合系数 (Mixing Coefficient) 。 控制梯形近似的形状。Mamba-3 将其设为可学习参数,允许模型自适应选择更新策略。 • λt=1\lambda_t=1λt=1:退化为 Mamba-2 (Euler)。 • λt=0.5\lambda_t=0.5λt=0.5:标准梯形法则。 |
| Δt\Delta tΔt | >0>0>0 (Learnable) | R1\mathbb{R}^1R1 | 时间步长 (Step Size) 。 控制离散化的粒度,同时也充当"选择性机制"中的门控,决定了模型关注当前输入的程度。 |
| AtA_tAt | <0<0<0 (Learnable) | R1\mathbb{R}^1R1 | 系统矩阵 (System Matrix) 。 在 Mamba 架构中通常被简化为对角矩阵或标量。决定了记忆的衰减速度(AtA_tAt 越小,遗忘越快)。 |
| αt\alpha_tαt | eΔtAte^{\Delta t A_t}eΔtAt | (0,1)(0, 1)(0,1) | 衰减因子 (Decay Factor) 。 状态 ht−1h_{t-1}ht−1 传递到 hth_tht 时的保留比例。 |
| βt\beta_tβt | (1−λt)Δtαt(1 - \lambda_t)\Delta t \alpha_t(1−λt)Δtαt | R1\mathbb{R}^1R1 | 历史输入权重 。 上一时刻输入 xt−1x_{t-1}xt−1 对当前状态更新的贡献系数。 |
| γt\gamma_tγt | λtΔt\lambda_t \Delta tλtΔt | R1\mathbb{R}^1R1 | 当前输入权重 。 当前时刻输入 xtx_txt 对当前状态更新的贡献系数。 |
注意到公式中 βt\beta_tβt 和 γt\gamma_tγt 的存在,意味着 hth_tht 不再仅仅是 ht−1h_{t-1}ht−1 和 xtx_txt 的函数,它显式地依赖了 xt−1x_{t-1}xt−1。这在离散序列模型中引入了一种 "一步回看"(One-step Lookback) 机制。
3. 架构洞察:梯形法则即卷积 (Discretization as Convolution)
Mamba-3 最精妙的理论贡献在于证明了:更精确的离散化方法等价于引入了一个隐式的卷积层。
3.1 卷积视角的证明
观察递归项的输入部分:
Update Term=βt(Bt−1xt−1)+γt(Btxt) \text{Update Term} = \beta_t (B_{t-1} x_{t-1}) + \gamma_t (B_t x_t) Update Term=βt(Bt−1xt−1)+γt(Btxt)
这本质上是一个长度为 2 的因果卷积 (Causal Convolution of size 2) ,作用于投影后的输入 BxBxBx 上。卷积核的权重由 βt\beta_tβt 和 γt\gamma_tγt 动态决定。
3.2 SSD 矩阵分解 (Matrix Decomposition)
在结构化状态空间对偶 (SSD) 的视角下,Mamba-3 的掩码矩阵 LMamba-3L_{\text{Mamba-3}}LMamba-3 可以被优雅地分解。
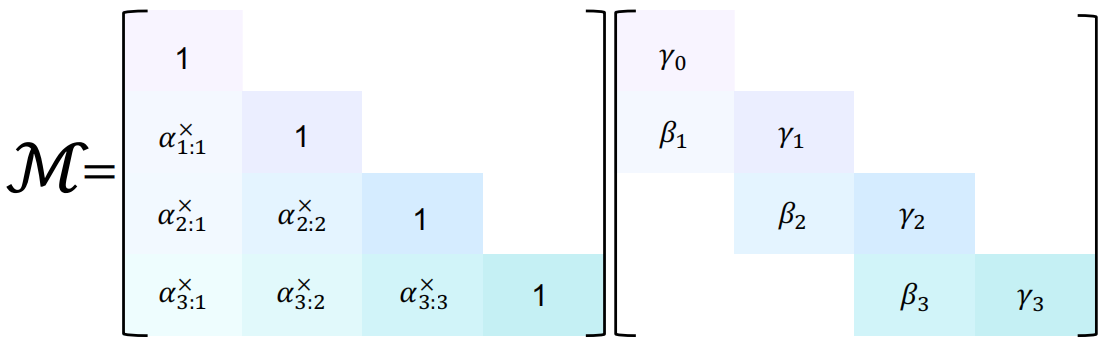
图2:SSD 掩码矩阵分解
- 来源 :论文 Figure 1 (Left Panel)。
- 说明 :展示一个全下三角矩阵如何被拆解为"衰减矩阵"与"双对角线卷积矩阵"的乘积。
- 左侧矩阵(Decay):主对角线为 1,下三角元素为累积衰减 α\alphaα。代表长时记忆。
- 右侧矩阵(Conv):仅主对角线(γ\gammaγ)和次对角线(β\betaβ)有值。代表局部卷积。
公式表达:
LMamba-3=LDecay×LConv L_{\text{Mamba-3}} = L_{\text{Decay}} \times L_{\text{Conv}} LMamba-3=LDecay×LConv
γ000...γ10......γ2\]=\[100α110α2α1α21\]×\[γ000β1γ100β2γ2\] \\begin{bmatrix} \\gamma_0 \& 0 \& 0 \\\\ \\dots \& \\gamma_1 \& 0 \\\\ \\dots \& \\dots \& \\gamma_2 \\end{bmatrix}= \\begin{bmatrix} 1 \& 0 \& 0 \\\\ \\alpha_1 \& 1 \& 0 \\\\ \\alpha_{2}\\alpha_1 \& \\alpha_2 \& 1 \\end{bmatrix} \\times \\begin{bmatrix} \\gamma_0 \& 0 \& 0 \\\\ \\beta_1 \& \\gamma_1 \& 0 \\\\ 0 \& \\beta_2 \& \\gamma_2 \\end{bmatrix} γ0......0γ1...00γ2 = 1α1α2α101α2001 × γ0β100γ1β200γ2 #### 3.3 架构精简:告别显式卷积 在 Mamba-1 和 Mamba-2 中,为了增强局部特征提取能力并平滑输入,架构中显式加入了一个 1D 卷积层(通常 kernel size=4)。 **Mamba-3 的发现** : 由于梯形离散化本身就内建了一个 222-tap 的自适应卷积,配合在 BBB 和 CCC 投影层引入的偏置项(Bias),模型已经具备了足够的局部处理能力。 * **结论**:Mamba-3 移除了显式的 Short Convolution 层。 * **收益**:减少了参数量,简化了推理时的计算图,同时保持甚至提升了语言建模的 Perplexity 指标。 *** ** * ** *** ### 4. 总结 (Summary) | 特性 | Mamba-2 (Euler) | Mamba-3 (Trapezoidal) | 优势分析 | |:----------|:----------------------------|:---------------------------------|:-------------| | **逼近精度** | 一阶 (O(Δt)O(\\Delta t)O(Δt)) | 二阶 (O(Δt2)O(\\Delta t\^2)O(Δt2)) | 捕捉更精细的动态变化 | | **离散化公式** | 仅依赖 xtx_txt | 依赖 xtx_txt 和 xt−1x_{t-1}xt−1 | 信息利用率更高 | | **等效结构** | 纯递归 (RNN) | 递归 + 隐式卷积 (RNN + Conv) | 融合了局部平滑与长程记忆 | | **架构影响** | 需额外 Conv 层 | **移除显式 Conv 层** | 架构更纯粹,效率更高 | Mamba-3 通过回归数值分析的基础原理,证明了 **"更好的数学近似 = 更强的模型架构"** 。这一改进不仅提升了理论优美度,更在实际的语言建模任务中带来了实质性的性能飞跃。