目录

1.摘要
量子云计算(QCC)使应用用户能够高效处理计算密集、资源需求高的复杂问题,本文研究量子云环境下的量子任务卸载(QTO),在综合考虑能耗、时延、服务成本和负载均衡的基础上,引入任务紧急性,构建了带预算与截止期限约束的量子任务卸载问题(QTOP),并证明其为 NP 完全问题。为此,本文提出了一种量子启发粒子群算法(QPSO),设计了新的量子粒子编码与线性哈希解码机制以生成可行卸载方案,并通过引入惩罚变量的适应度函数有效排除不可行解。
2.问题描述
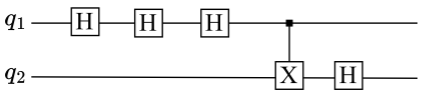
在 QCC 中,量子节点(QNd)由量子处理单元(QPU)支撑,用于执行以量子电路形式表示的量子任务。QPU 通过量子门对一个或多个量子比特(qubit)进行计算。
系统模型
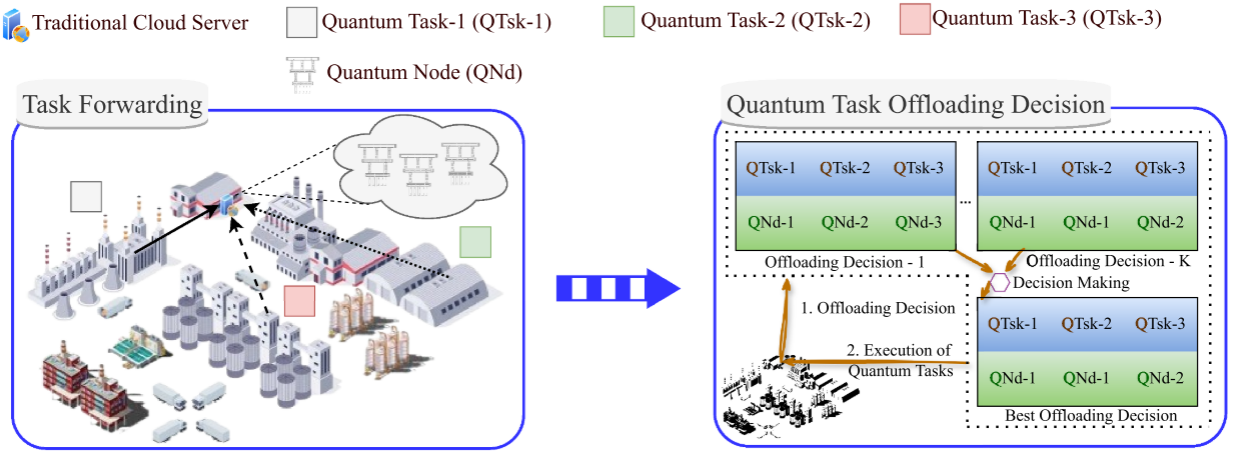
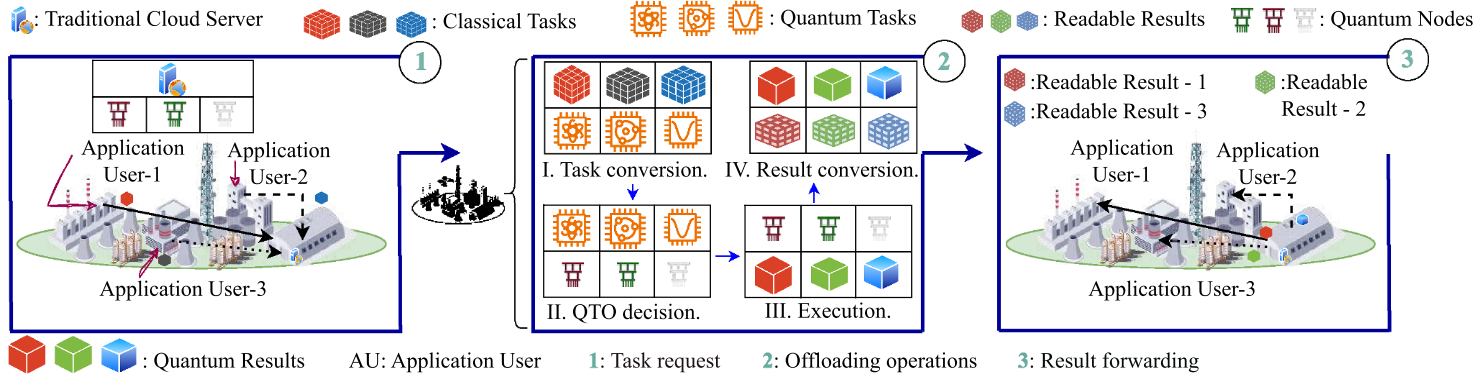
本文构建了一个量子云计算系统模型,应用用户 (AUs)将经典任务提交至传统云服务器,经量子应用转换为量子任务 (QTsk),并由量子任务卸载 (QTO)机制决定其在量子节点(QNd) 上的执行位置。系统包含 M M M个量子任务和 N N N个量子节点,每个QNd 配备量子处理单元 (QPU),任务在节点上顺序执行,需满足量子比特数量、时延和预算约束。
计算时延:
δ g j c = ξ g j ϕ g d ⋅ ϕ g s n j s \delta_{gj}^c=\xi_{gj}\frac{\phi_g^d\cdot\phi_g^s}{n_j^s} δgjc=ξgjnjsϕgd⋅ϕgs
总任务时延:
δ g = δ g j c + ∑ r = 1 l δ r j c \delta_g=\delta_{gj}^c+\sum_{r=1}^l\delta_{rj}^c δg=δgjc+r=1∑lδrjc
系统总时延:
δ t = max j ∈ [ 1 , N ] δ j \delta_t=\max_{j\in[1,N]}\delta_j δt=j∈[1,N]maxδj
总能耗:
e t = ∑ g = 1 M e g c e_t=\sum_{g=1}^Me_g^c et=g=1∑Megc
负载均衡:
V a r ( σ ) = 1 N ∑ j = 1 N ( σ j − σ ˉ ) 2 \mathrm{Var}(\sigma)=\frac{1}{N}\sum_{j=1}^N(\sigma_j-\bar{\sigma})^2 Var(σ)=N1j=1∑N(σj−σˉ)2
任务执行价格:
P g = ρ j ⋅ δ g j c , P t = ∑ g = 1 M P g \mathcal{P}g=\rho_j\cdot\delta{gj}^c,\quad\mathcal{P}t=\sum{g=1}^M\mathcal{P}_g Pg=ρj⋅δgjc,Pt=g=1∑MPg
目标函数:
min { δ t , e t , V a r ( σ ) , P t } \min\{\delta_t,e_t,\mathrm{Var}(\sigma),\mathcal{P}_t\} min{δt,et,Var(σ),Pt}
3.提出的量子启发粒子群算法(QPSO)
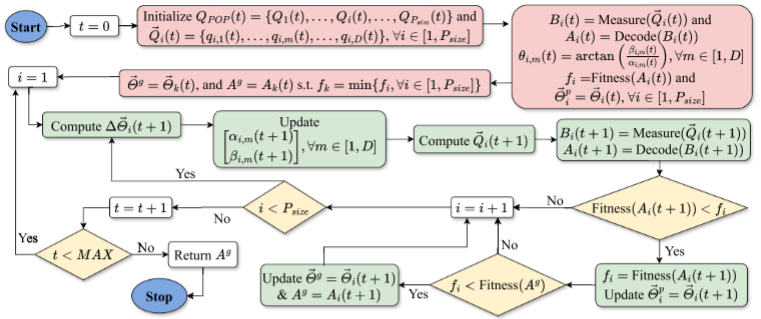
QPSO 使用量子粒子(QP)对解进行编码,每个 QP 由多个量子比特组成,其概率幅度以归一化随机值初始化,从而在搜索初期保持较高的不确定性和多样性。
量子种群初始化
在量子种群初始化阶段,每个量子粒子编码一个完整的量子任务卸载方案。针对每个量子任务,其可选量子节点数决定所需的量子比特数量:
Q B g = ⌈ log 2 ( o g ) ⌉ QB_g=\lceil\log_2(o_g)\rceil QBg=⌈log2(og)⌉
量子粒子的维度为:
D = ∑ g = 1 M Q B g D=\sum_{g=1}^MQB_g D=g=1∑MQBg
其中, M M M为量子任务总数,通过按顺序分配量子比特,每个 QP 能同时表示所有任务的卸载決策。

量子种群测量
在 QPSO 中,通过对量子粒子 Q ⃗ i ( t ) \vec{Q}i(t) Q i(t) 进行测量,将其映射为对应的二进制粒子 B i ( t ) B_i(t) Bi(t),以便进行适应度评估与后续操作。测量过程基于量子概率机制:对每个量子比特 q i , m q{i,m} qi,m,生成一个[0,1]区间的随机数,并与其振幅平方 ∣ α i , m ∣ 2 |\alpha_{i,m}|^2 ∣αi,m∣2比较,从而以概率方式确定二进制取值 b i , m ∈ { 0 , 1 } b_{i,m}\in\{0,1\} bi,m∈{0,1}。

二进制种群编码
在 QPSO 中,测量得到的二进制粒子 B i ( t ) B_i(t) Bi(t)被划分为 M M M个片段,每个片段对应一个量子
任务 ϕ g \phi_g ϕg,其长度为 Q B g QB_g QBg:
D = ∑ g = 1 M Q B g D=\sum_{g=1}^MQB_g D=g=1∑MQBg
每个片段通过二进制到十进制解码,生成解码粒子:
A i ( t ) = { a i , 1 ( t ) , a i , 2 ( t ) , ... , a i , M ( t ) } A_i(t)=\{a_{i,1}(t),a_{i,2}(t),\ldots,a_{i,M}(t)\} Ai(t)={ai,1(t),ai,2(t),...,ai,M(t)}
其中 a i , g ( t ) a_{i,g}(t) ai,g(t)表示任务 ϕ g \phi_g ϕg被分配的量子节点索引。
若解码值超出该任务可选量子节点数量 o g o_g og,则采用线性哈希映射:
a i , g ( t ) = a i , g ( t ) m o d o g a_{i,g}(t)=a_{i,g}(t)\mathrm{mod}o_g ai,g(t)=ai,g(t)modog

量子粒子更新
QPSO通过角度形式描述量子粒子状态,并结合个体最优和全局最优信息对粒子进行迭代更新,角度增量更新:
Δ Θ ⃗ i ( t + 1 ) = w Δ Θ ⃗ i ( t ) + κ 1 r 1 ( Θ ⃗ i p ( t ) − Θ ⃗ i ( t ) ) + κ 2 r 2 ( Θ ⃗ g ( t ) − Θ ⃗ i ( t ) ) \Delta\vec{\Theta}_i(t+1)=w\Delta\vec{\Theta}_i(t)+\kappa_1r_1(\vec{\Theta}_i^p(t)-\vec{\Theta}_i(t))+\kappa_2r_2(\vec{\Theta}^g(t)-\vec{\Theta}_i(t)) ΔΘ i(t+1)=wΔΘ i(t)+κ1r1(Θ ip(t)−Θ i(t))+κ2r2(Θ g(t)−Θ i(t))
量子比特旋转更新:
α i , m ( t + 1 ) β i , m ( t + 1 ) \] = R ( Δ θ i , m ( t ) ) \[ α i , m ( t ) β i , m ( t ) \] \\begin{bmatrix}\\alpha_{i,m}(t+1)\\\\\\beta_{i,m}(t+1)\\end{bmatrix}=R(\\Delta\\theta_{i,m}(t))\\begin{bmatrix}\\alpha_{i,m}(t)\\\\\\beta_{i,m}(t)\\end{bmatrix} \[αi,m(t+1)βi,m(t+1)\]=R(Δθi,m(t))\[αi,m(t)βi,m(t)

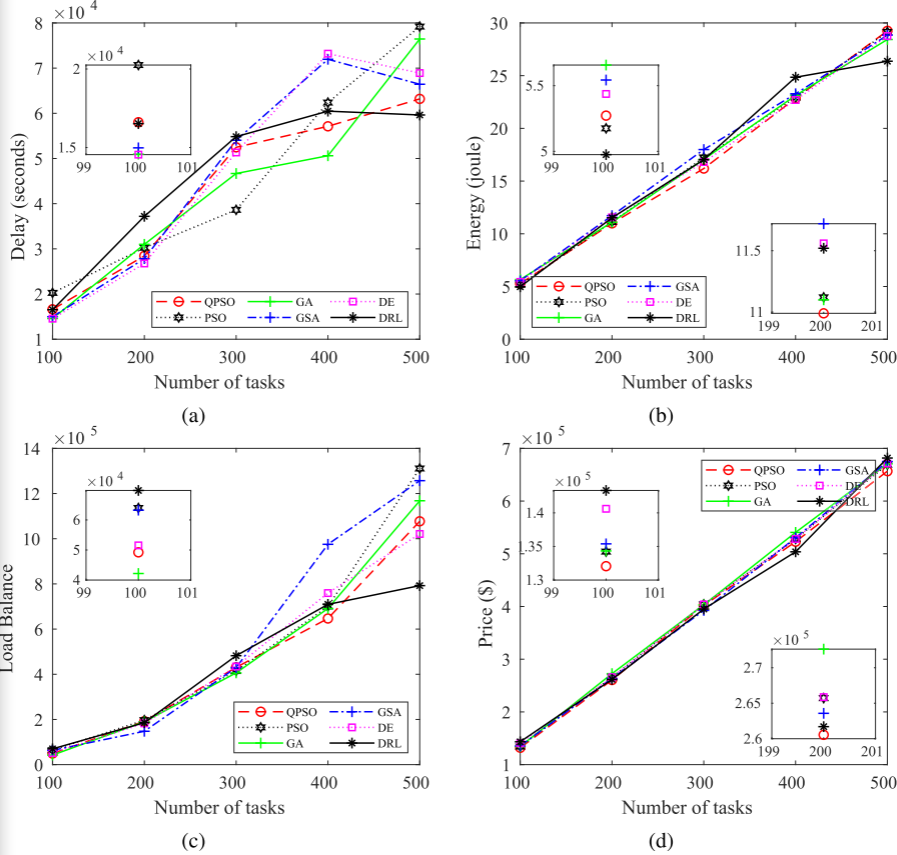
4.结果展示
5.参考文献
1\] Ghosh S, Kuila P. Cost-Efficient Quantum Cloud Task Offloading with Quantum-Inspired Particle Swarm Optimization\[J\]. Future Generation Computer Systems, 2025: 108095. ### 6.代码获取 xx ### 7.算法辅导·应用定制·读者交流 xx