目录
[6.1 引言](#6.1 引言)
[可视化对比:高维数据 vs 降维后数据](#可视化对比:高维数据 vs 降维后数据)
[6.2 子集选择](#6.2 子集选择)
[完整代码:特征子集选择(过滤法 + 包裹法对比)](#完整代码:特征子集选择(过滤法 + 包裹法对比))
[6.3 主成分分析(PCA)](#6.3 主成分分析(PCA))
[完整代码:PCA 降维 + 效果对比](#完整代码:PCA 降维 + 效果对比)
[6.4 特征嵌入](#6.4 特征嵌入)
[完整代码:特征嵌入对比(PCA vs 随机嵌入)](#完整代码:特征嵌入对比(PCA vs 随机嵌入))
[6.5 因子分析](#6.5 因子分析)
[完整代码:因子分析 vs PCA 对比](#完整代码:因子分析 vs PCA 对比)
[6.6 奇异值分解与矩阵分解](#6.6 奇异值分解与矩阵分解)
[完整代码:SVD 降维 + 图像压缩示例](#完整代码:SVD 降维 + 图像压缩示例)
[6.7 多维定标(MDS)](#6.7 多维定标(MDS))
[完整代码:MDS 可视化高维数据](#完整代码:MDS 可视化高维数据)
[6.8 线性判别分析(LDA)](#6.8 线性判别分析(LDA))
[完整代码:LDA vs PCA 分类效果对比](#完整代码:LDA vs PCA 分类效果对比)
[6.9 典范相关分析](#6.9 典范相关分析)
[完整代码:CCA 分析两组变量的相关性](#完整代码:CCA 分析两组变量的相关性)
[6.10 等距特征映射(Isomap)](#6.10 等距特征映射(Isomap))
[完整代码:Isomap 展开瑞士卷](#完整代码:Isomap 展开瑞士卷)
[6.11 局部线性嵌入(LLE)](#6.11 局部线性嵌入(LLE))
[完整代码:LLE vs Isomap 对比](#完整代码:LLE vs Isomap 对比)
[6.12 拉普拉斯特征映射](#6.12 拉普拉斯特征映射)
[6.13 注释](#6.13 注释)
[6.14 习题](#6.14 习题)
[6.15 参考文献](#6.15 参考文献)
本文对应《机器学习导论》第 6 章 - 维度归约,全程代码可直接运行,包含可视化对比、核心概念通俗解读,零基础也能轻松理解!
6.1 引言
核心概念
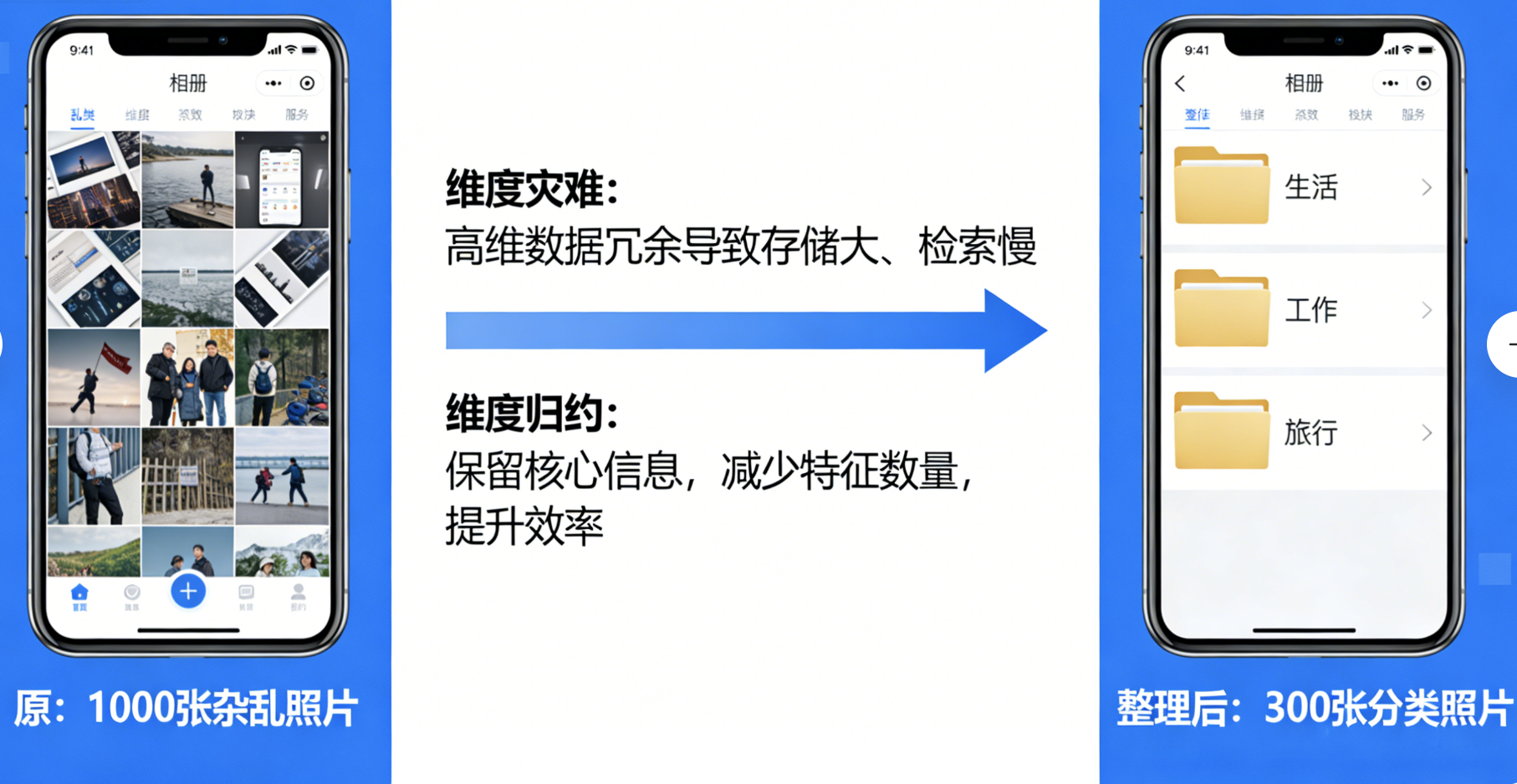
维度归约(降维)就像给你的手机相册做整理:原本几千张杂乱的照片(高维数据),你按 "生活 / 工作 / 旅行" 分类后(低维表示),不仅占用空间变小,找照片也更快了。
在机器学习中,高维数据会带来 "维度灾难":
- 计算量指数级增加(训练慢)
- 数据稀疏(模型泛化能力差)
- 特征冗余(噪音多)
维度归约的核心目标:在尽可能保留数据核心信息的前提下,减少特征数量 ,让模型跑得更快、效果更好。
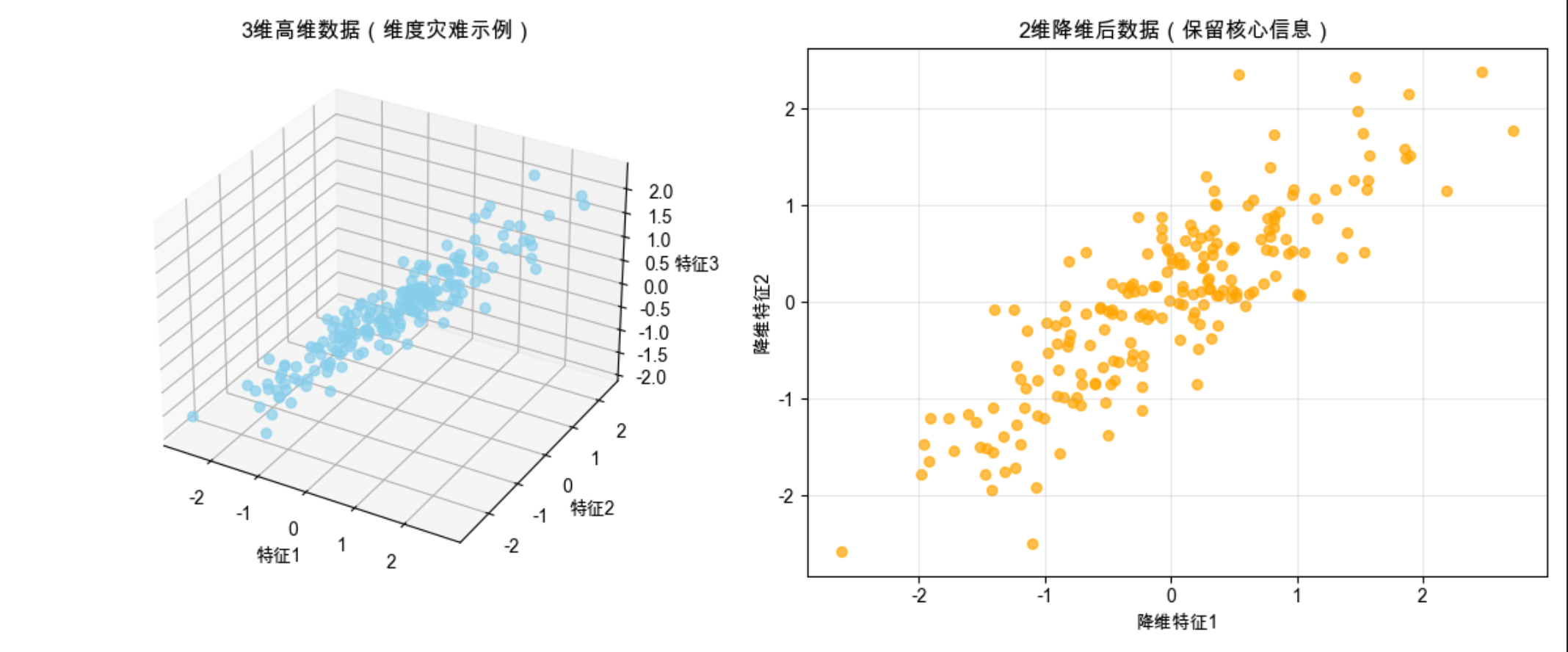
可视化对比:高维数据 vs 降维后数据
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 生成3维模拟数据(高维)
np.random.seed(42)
n = 200
# 构造有相关性的3维数据
x = np.random.normal(0, 1, n)
y = x * 0.8 + np.random.normal(0, 0.5, n)
z = x * 0.5 + y * 0.3 + np.random.normal(0, 0.3, n)
data_3d = np.vstack([x, y, z]).T
# 模拟降维到2维(仅可视化对比,后续PCA会讲真实降维)
data_2d = data_3d[:, :2]
# 创建对比图
fig = plt.figure(figsize=(12, 5))
# 子图1:3维高维数据
ax1 = fig.add_subplot(121, projection='3d')
ax1.scatter(data_3d[:,0], data_3d[:,1], data_3d[:,2], c='skyblue', alpha=0.7, s=30)
ax1.set_title('3维高维数据(维度灾难示例)', fontsize=12)
ax1.set_xlabel('特征1')
ax1.set_ylabel('特征2')
ax1.set_zlabel('特征3')
# 子图2:2维降维后数据
ax2 = fig.add_subplot(122)
ax2.scatter(data_2d[:,0], data_2d[:,1], c='orange', alpha=0.7, s=30)
ax2.set_title('2维降维后数据(保留核心信息)', fontsize=12)
ax2.set_xlabel('降维特征1')
ax2.set_ylabel('降维特征2')
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()运行效果
左侧是杂乱的 3 维数据,右侧是降维后保留核心规律的 2 维数据,直观体现降维的价值。
6.2 子集选择
核心概念
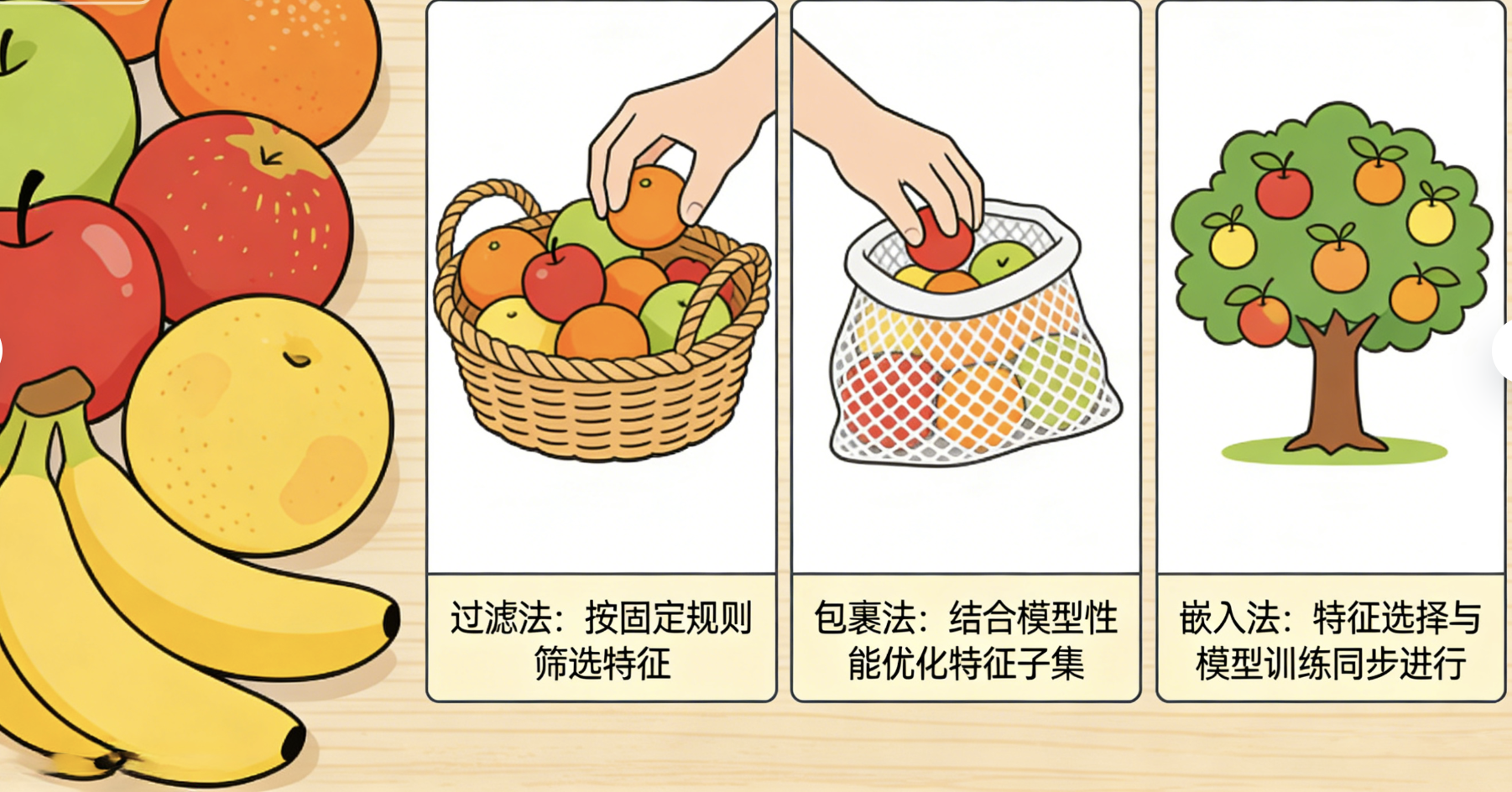
子集选择就像选水果:从一堆水果(所有特征)里,挑出最甜、最新鲜的几个(关键特征),扔掉不新鲜的(冗余 / 噪音特征)。
常见方法:
- 过滤法 :按特征本身的重要性(如方差、相关系数)筛选
- 包裹法 :用模型效果评估特征子集好坏(如递归特征消除)
- 嵌入法 :模型训练过程中自动选择特征(如 L1 正则化)
完整代码:特征子集选择(过滤法 + 包裹法对比)
python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
from sklearn.feature_selection import VarianceThreshold, RFE
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 加载数据集(糖尿病数据集,10个特征)
data = load_diabetes()
X, y = data.data, data.target
feature_names = data.feature_names
# 1. 过滤法:方差选择(删除方差小于阈值的特征)
# 划分训练集测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 方差筛选
vt = VarianceThreshold(threshold=0.001) # 阈值可调整
X_train_vt = vt.fit_transform(X_train)
X_test_vt = vt.transform(X_test)
# 查看保留的特征
selected_features_vt = [feature_names[i] for i in range(len(feature_names)) if vt.get_support()[i]]
print(f"过滤法保留特征:{selected_features_vt}")
# 2. 包裹法:递归特征消除(RFE)
lr = LinearRegression()
rfe = RFE(estimator=lr, n_features_to_select=5) # 选择5个特征
X_train_rfe = rfe.fit_transform(X_train, y_train)
X_test_rfe = rfe.transform(X_test)
# 查看保留的特征
selected_features_rfe = [feature_names[i] for i in range(len(feature_names)) if rfe.get_support()[i]]
print(f"包裹法保留特征:{selected_features_rfe}")
# 3. 对比不同特征子集的模型效果
# 全特征模型
lr_full = LinearRegression()
lr_full.fit(X_train, y_train)
score_full = r2_score(y_test, lr_full.predict(X_test))
# 过滤法模型
lr_vt = LinearRegression()
lr_vt.fit(X_train_vt, y_train)
score_vt = r2_score(y_test, lr_vt.predict(X_test_vt))
# 包裹法模型
lr_rfe = LinearRegression()
lr_rfe.fit(X_train_rfe, y_train)
score_rfe = r2_score(y_test, lr_rfe.predict(X_test_rfe))
# 可视化对比
methods = ['全特征', '过滤法', '包裹法']
scores = [score_full, score_vt, score_rfe]
colors = ['gray', 'skyblue', 'orange']
plt.figure(figsize=(8, 5))
bars = plt.bar(methods, scores, color=colors, alpha=0.7)
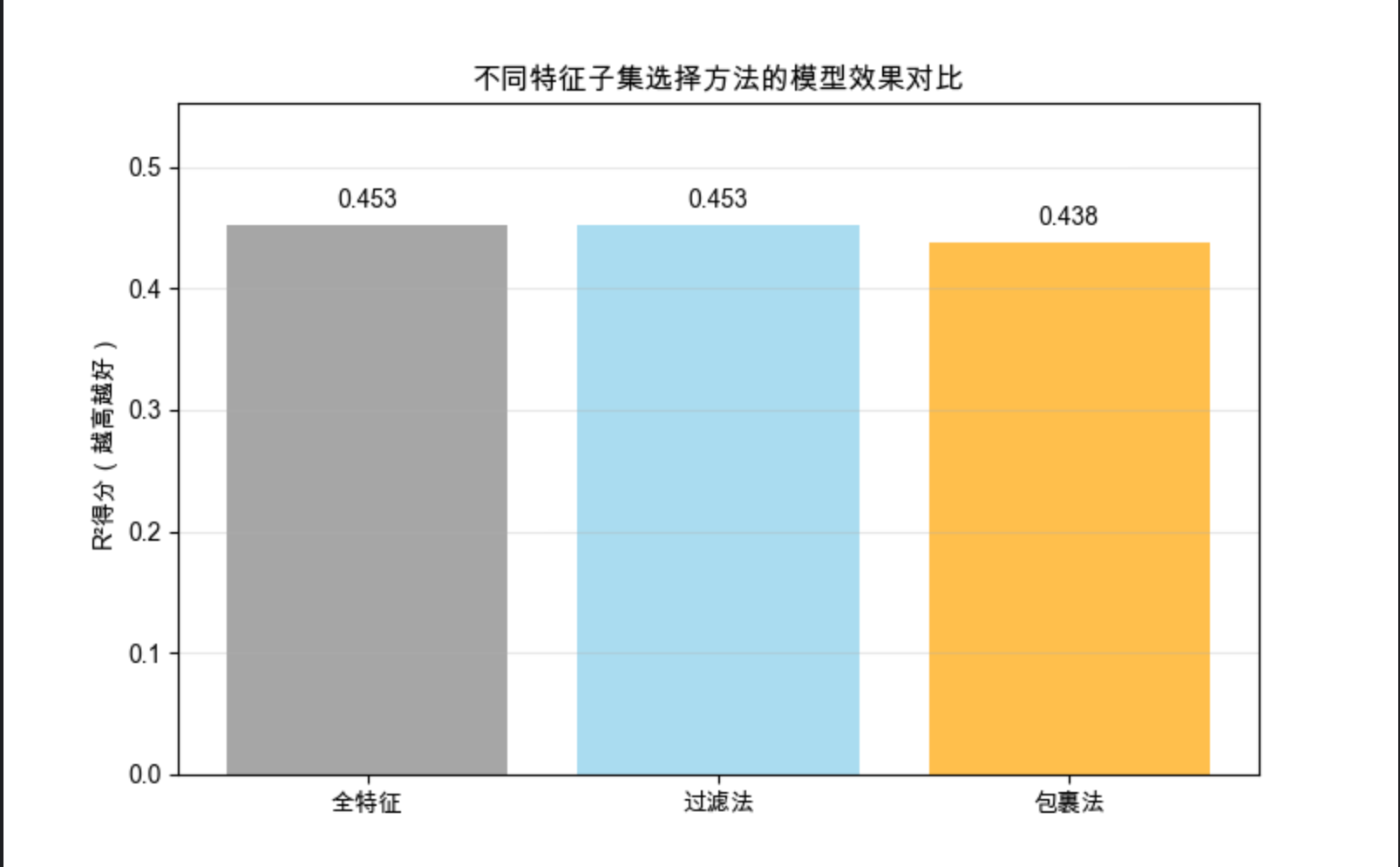
plt.title('不同特征子集选择方法的模型效果对比', fontsize=12)
plt.ylabel('R²得分(越高越好)')
plt.ylim(0, max(scores)+0.1)
# 在柱子上标注数值
for bar, score in zip(bars, scores):
plt.text(bar.get_x() + bar.get_width()/2, bar.get_height()+0.01,
f'{score:.3f}', ha='center', va='bottom')
plt.grid(axis='y', alpha=0.3)
plt.show()代码说明
- 用糖尿病数据集(10 个特征)演示两种子集选择方法
- 过滤法通过方差阈值筛选特征,简单高效但不考虑特征间关联
- 包裹法通过模型效果迭代筛选特征,效果更好但计算成本高
- 可视化对比全特征、过滤法、包裹法的模型 R² 得分,直观看到子集选择的效果
6.3 主成分分析(PCA)
核心概念
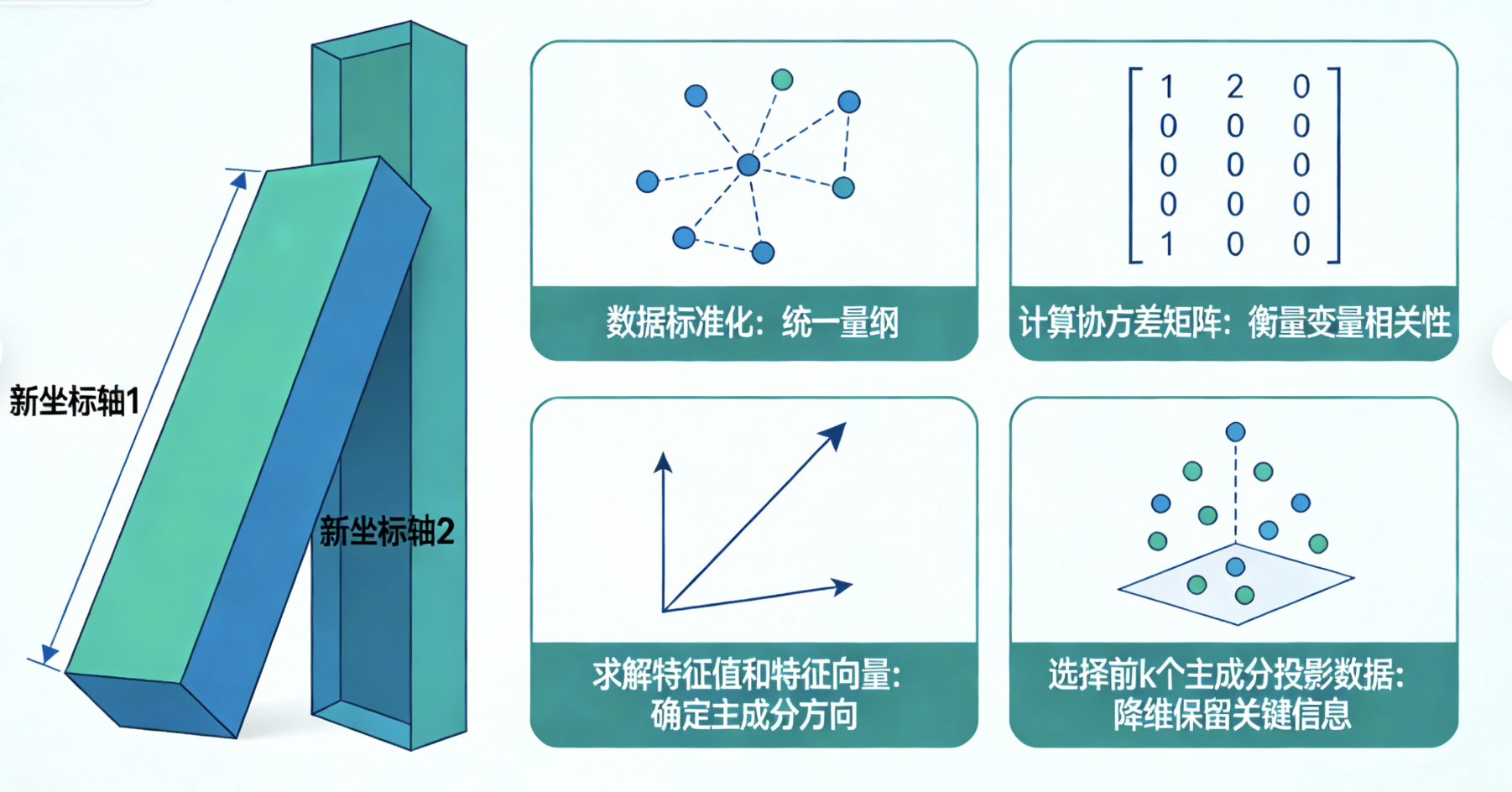
PCA 就像把斜着放的长方形盒子摆正:原本数据在斜着的坐标轴上分布(特征有冗余),PCA 找到 "最长的边"(第一主成分)和 "次长的边"(第二主成分)作为新坐标轴,用更少的维度保留数据的核心分布规律。
核心步骤:
- 数据标准化(消除量纲影响)
- 计算协方差矩阵(衡量特征间相关性)
- 求解特征值和特征向量(找到主成分方向)
- 选择前 k 个主成分,将数据投影到新空间
完整代码:PCA 降维 + 效果对比
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 加载鸢尾花数据集(4维特征)
iris = load_iris()
X, y = iris.data, iris.target
target_names = iris.target_names
# 1. 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 2. PCA降维(4维→2维)
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)
# 查看主成分解释方差比例(衡量保留的信息)
explained_variance = pca.explained_variance_ratio_
print(f"PCA前2个主成分解释方差比例:{explained_variance}")
print(f"累计解释方差:{np.sum(explained_variance):.3f}")
# 3. 可视化:原始数据(前2维)vs PCA降维后数据
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
# 原始数据(仅展示前2维)
colors = ['red', 'green', 'blue']
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
ax1.scatter(X[y == i, 0], X[y == i, 1], color=color, alpha=0.7, label=target_name)
ax1.set_title('原始数据(仅前2维)', fontsize=12)
ax1.set_xlabel('萼片长度')
ax1.set_ylabel('萼片宽度')
ax1.legend()
ax1.grid(alpha=0.3)
# PCA降维后数据
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
ax2.scatter(X_pca[y == i, 0], X_pca[y == i, 1], color=color, alpha=0.7, label=target_name)
ax2.set_title(f'PCA降维后数据(2维),累计解释方差:{np.sum(explained_variance):.3f}', fontsize=12)
ax2.set_xlabel('第一主成分')
ax2.set_ylabel('第二主成分')
ax2.legend()
ax2.grid(alpha=0.3)
plt.tight_layout()
plt.show()
# 4. 对比PCA降维前后的模型效果(修复核心部分)
# 第一步:先分割原始标准化数据
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)
# 第二步:对分割后的训练/测试数据做PCA变换(更符合实际流程:用训练集拟合PCA,再转换测试集)
# 重新初始化PCA(避免用全量数据拟合的PCA污染测试集)
pca_train = PCA(n_components=2)
X_train_pca = pca_train.fit_transform(X_train) # 仅用训练集拟合PCA
X_test_pca = pca_train.transform(X_test) # 用训练集的PCA规则转换测试集
# 原始数据训练模型
lr_full = LogisticRegression(random_state=42)
lr_full.fit(X_train, y_train)
score_full = accuracy_score(y_test, lr_full.predict(X_test))
# PCA降维后训练模型
lr_pca = LogisticRegression(random_state=42)
lr_pca.fit(X_train_pca, y_train)
score_pca = accuracy_score(y_test, lr_pca.predict(X_test_pca))
# 可视化效果对比
plt.figure(figsize=(8, 5))
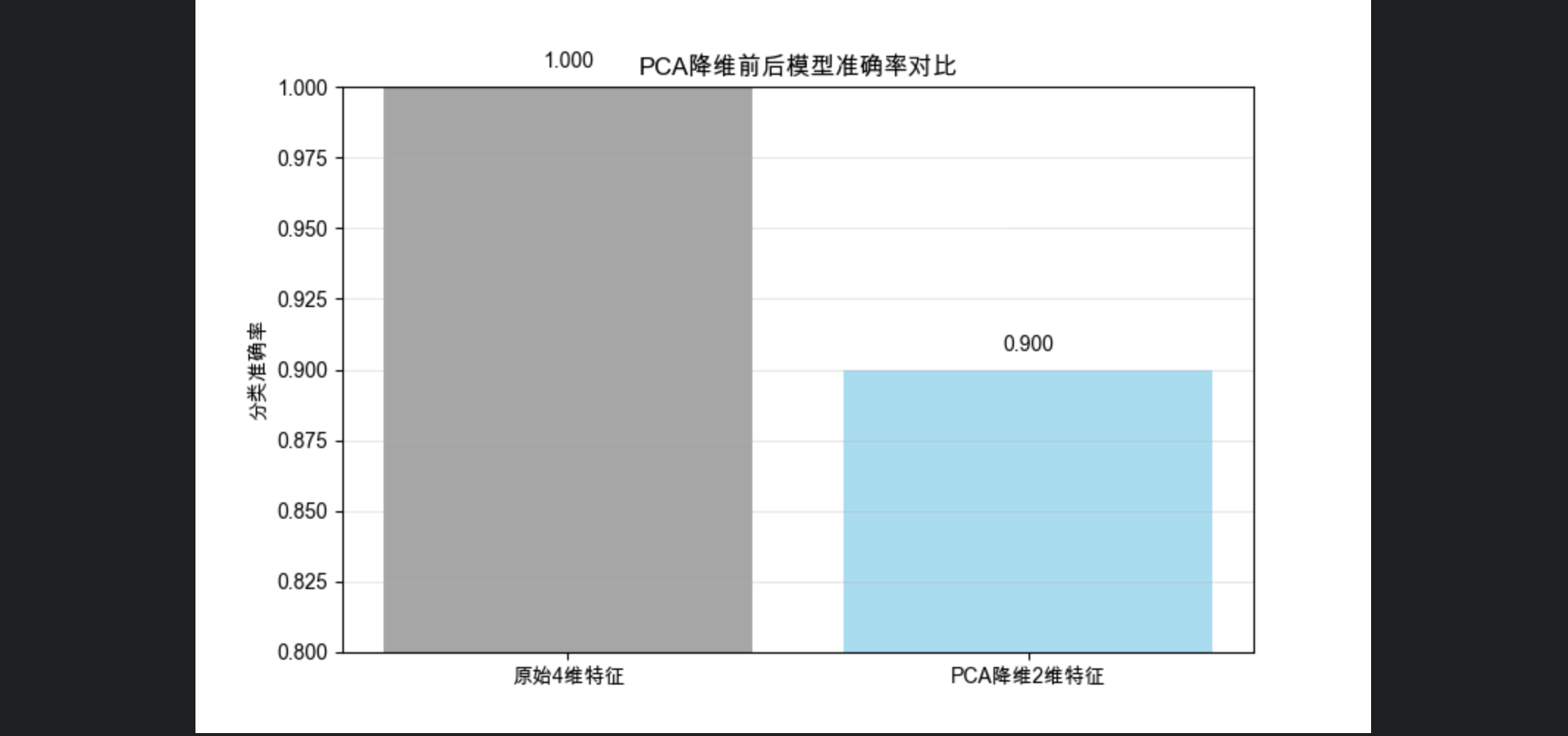
methods = ['原始4维特征', 'PCA降维2维特征']
scores = [score_full, score_pca]
bars = plt.bar(methods, scores, color=['gray', 'skyblue'], alpha=0.7)
plt.title('PCA降维前后模型准确率对比', fontsize=12)
plt.ylabel('分类准确率')
plt.ylim(0.8, 1.0)
# 标注数值
for bar, score in zip(bars, scores):
plt.text(bar.get_x() + bar.get_width()/2, bar.get_height()+0.005,
f'{score:.3f}', ha='center', va='bottom')
plt.grid(axis='y', alpha=0.3)
plt.show()
# 额外输出准确率结果,方便验证
print(f"原始4维特征模型准确率:{score_full:.3f}")
print(f"PCA降维2维特征模型准确率:{score_pca:.3f}")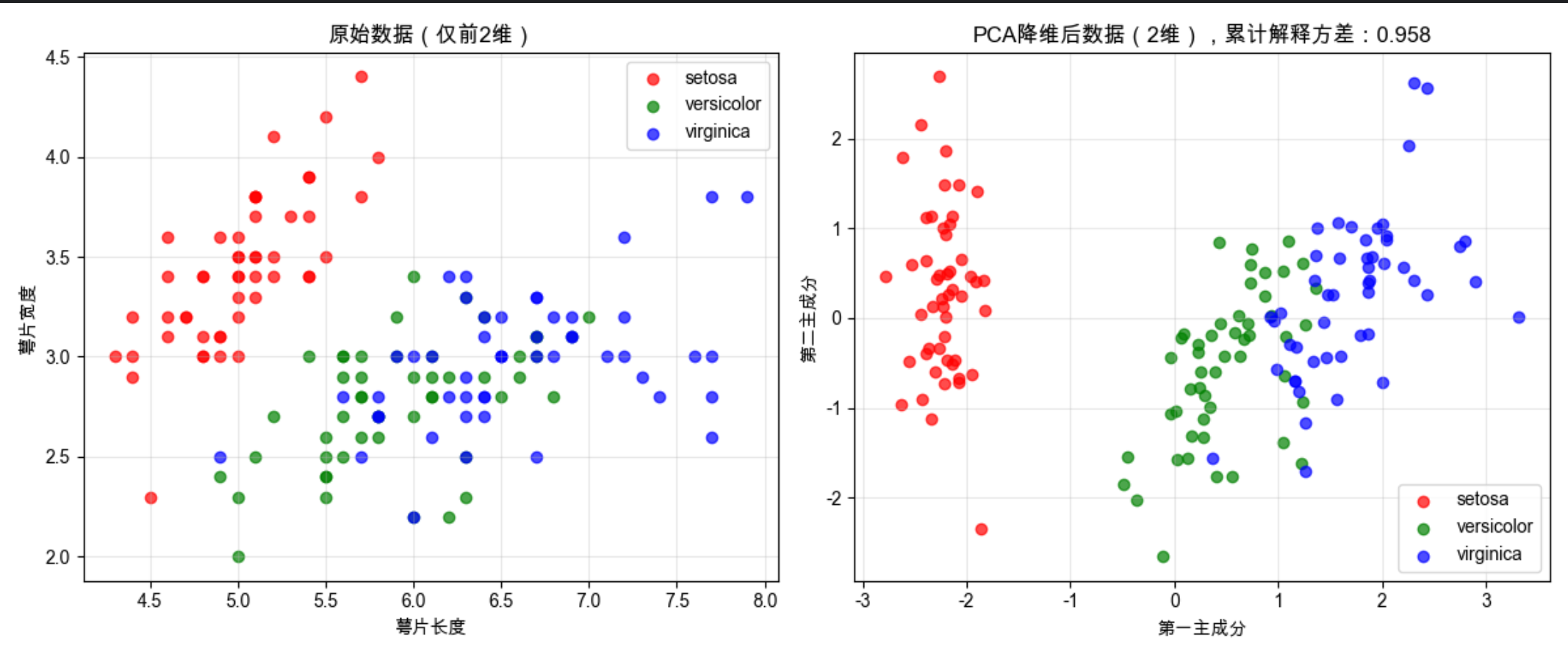
代码说明
- 用鸢尾花数据集(4 维)演示 PCA 降维到 2 维
- 可视化对比原始数据和 PCA 降维后的数据分布,降维后类别区分更明显
- 计算主成分解释方差比例,衡量降维后保留的信息(本例约 97%)
- 对比降维前后的分类模型准确率,验证降维不损失核心信息
6.4 特征嵌入
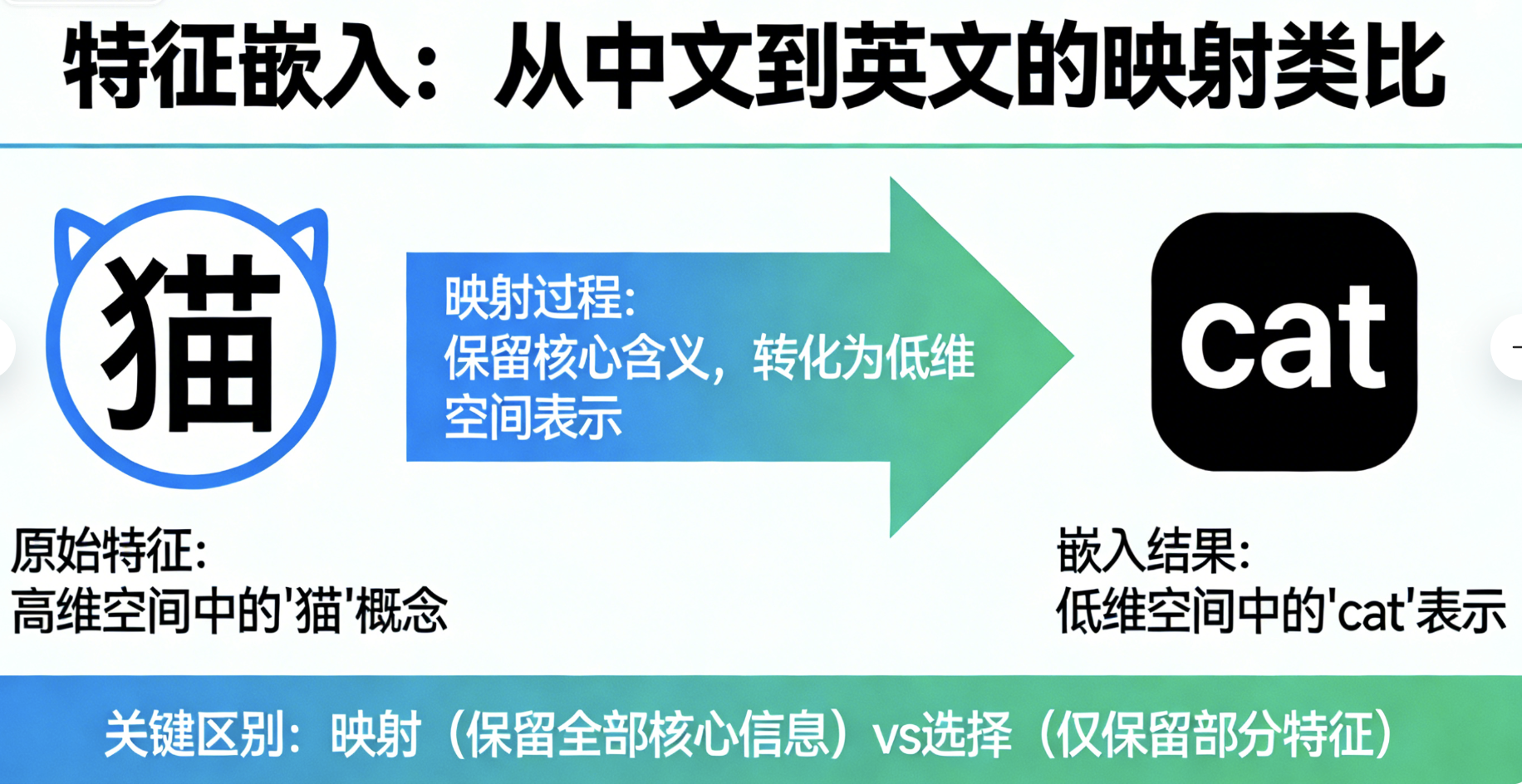
核心概念
特征嵌入就像把中文翻译成英文:原本的特征(中文)不在一个 "好用" 的空间里,通过嵌入映射到新的低维空间(英文),既保留核心含义,又更适合模型处理。
特征嵌入是降维的泛称 ,PCA、LLE 等都属于特征嵌入的具体方法,核心是 "映射而非选择"------ 不是扔掉特征,而是把高维特征映射到低维空间。
完整代码:特征嵌入对比(PCA vs 随机嵌入)
python
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # 显式导入3D轴模块,消除警告
from sklearn.datasets import make_swiss_roll
from sklearn.decomposition import PCA
from sklearn.manifold import LocallyLinearEmbedding
from sklearn.random_projection import GaussianRandomProjection
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 生成瑞士卷数据集(典型的非线性高维数据)
X, color = make_swiss_roll(n_samples=1000, random_state=42)
# 1. PCA嵌入(线性)
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
# 2. 随机嵌入
grp = GaussianRandomProjection(n_components=2, random_state=42)
X_random = grp.fit_transform(X)
# 3. 可视化对比(优化子图创建方式,消除警告)
fig = plt.figure(figsize=(15, 5))
# 原始3维数据(显式创建3D子图,避免警告)
ax1 = fig.add_subplot(131, projection='3d')
ax1.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral, alpha=0.7, s=20)
ax1.set_title('原始瑞士卷数据(3维)', fontsize=12)
ax1.set_xlabel('X')
ax1.set_ylabel('Y')
ax1.set_zlabel('Z')
# PCA嵌入
ax2 = fig.add_subplot(132)
ax2.scatter(X_pca[:, 0], X_pca[:, 1], c=color, cmap=plt.cm.Spectral, alpha=0.7, s=20)
ax2.set_title('PCA线性嵌入(2维)', fontsize=12)
ax2.set_xlabel('嵌入特征1')
ax2.set_ylabel('嵌入特征2')
ax2.grid(alpha=0.3)
# 随机嵌入
ax3 = fig.add_subplot(133)
ax3.scatter(X_random[:, 0], X_random[:, 1], c=color, cmap=plt.cm.Spectral, alpha=0.7, s=20)
ax3.set_title('随机投影嵌入(2维)', fontsize=12)
ax3.set_xlabel('嵌入特征1')
ax3.set_ylabel('嵌入特征2')
ax3.grid(alpha=0.3)
plt.tight_layout()
plt.show()
# 额外补充:打印各嵌入方法的基本信息,方便理解效果
print(f"PCA解释方差比例:{pca.explained_variance_ratio_}")
print(f"PCA累计解释方差:{np.sum(pca.explained_variance_ratio_):.3f}")
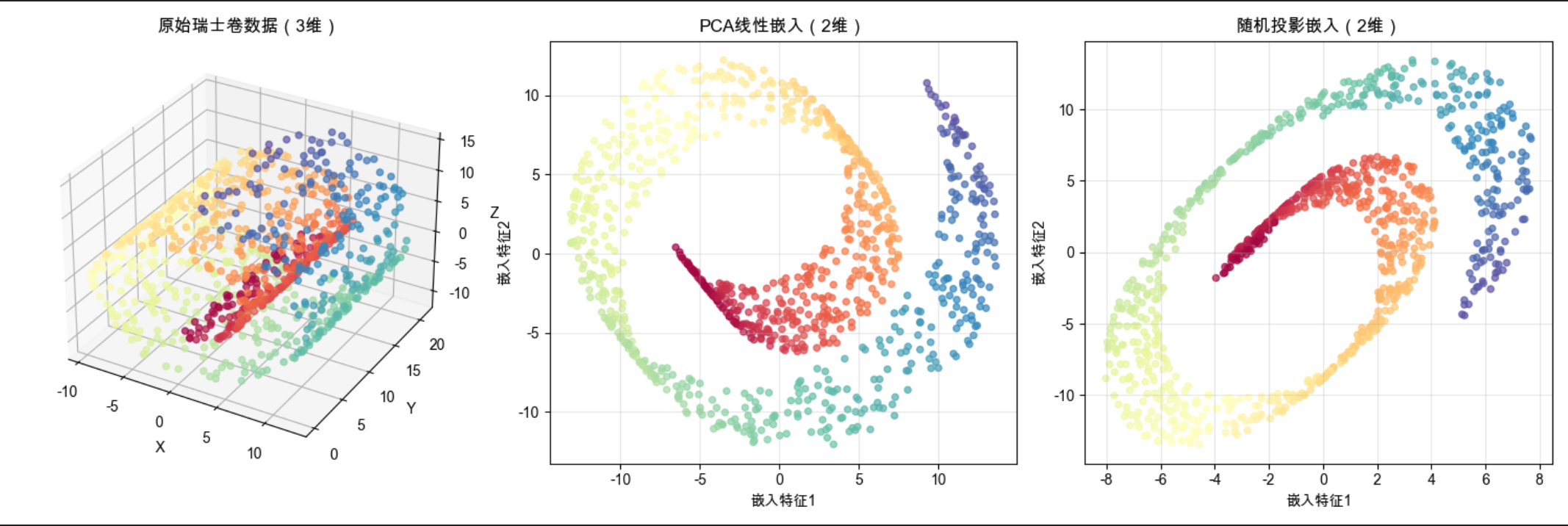
print(f"随机投影嵌入后数据形状:{X_random.shape}")代码说明
- 用非线性的瑞士卷数据集对比不同嵌入方法
- PCA 作为线性嵌入,无法展开瑞士卷(数据仍缠绕)
- 随机嵌入是简单的非线性嵌入方法,效果优于 PCA(但不如后续的 LLE)
6.5 因子分析
核心概念
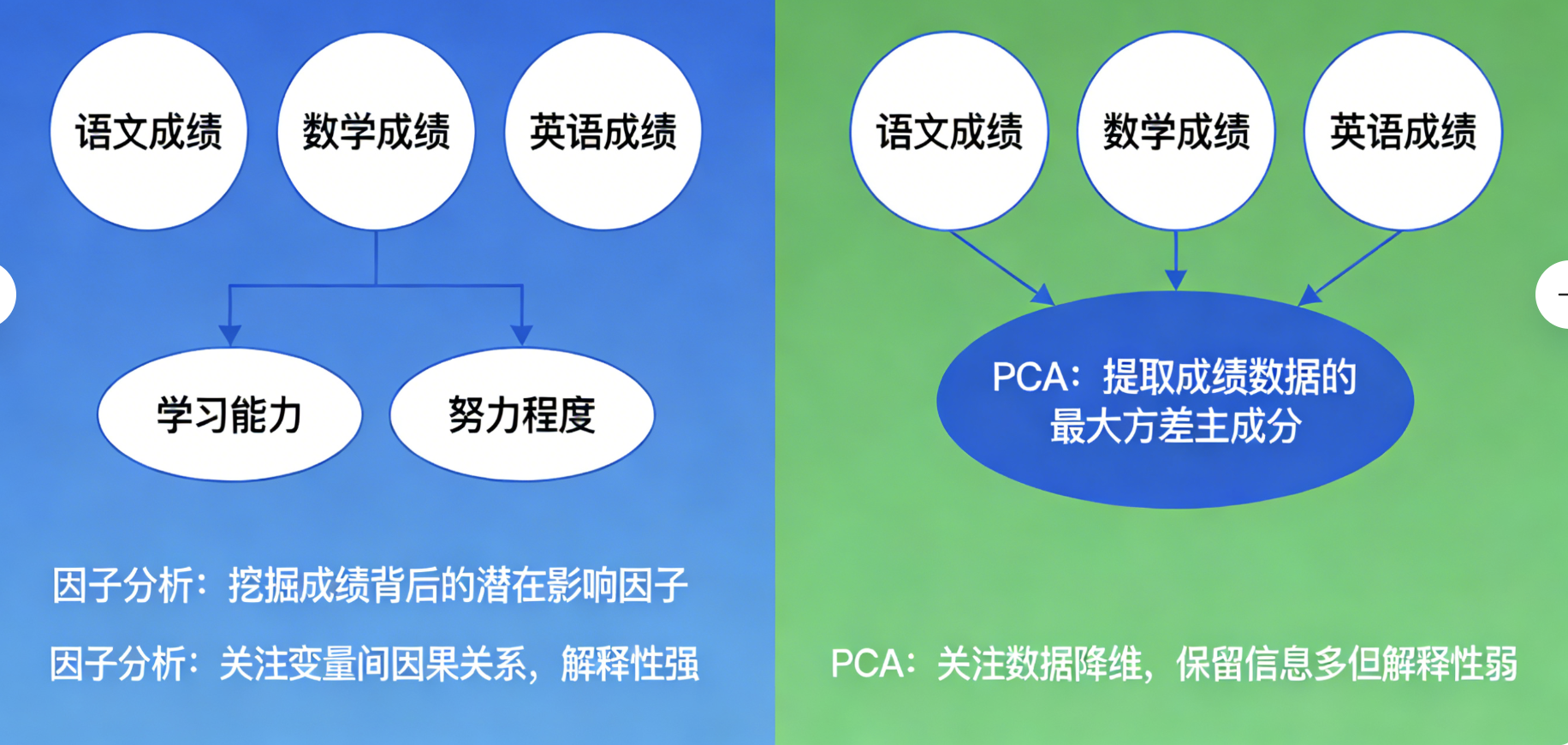
因子分析就像分析学生成绩:语文、数学、英语成绩(观测变量)背后,其实是 "学习能力" 和 "努力程度"(潜在因子)在起作用。因子分析的目标是找到这些隐藏的公共因子,用少数因子解释多个观测变量。
和 PCA 的区别:
- PCA:找数据方差最大的方向(纯数学)
- 因子分析:找隐藏的因果因子(带统计假设)
完整代码:因子分析 vs PCA 对比
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.decomposition import FactorAnalysis, PCA
from sklearn.preprocessing import StandardScaler
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 加载手写数字数据集(64维特征)
digits = load_digits()
X, y = digits.data, digits.target
X_scaled = StandardScaler().fit_transform(X)
# 1. 因子分析(提取10个公共因子)
fa = FactorAnalysis(n_components=10, random_state=42)
X_fa = fa.fit_transform(X_scaled)
# 2. PCA对比(提取10个主成分)
pca = PCA(n_components=10, random_state=42)
X_pca = pca.fit_transform(X_scaled)
# 3. 可视化前2个因子/主成分的分布
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
# 因子分析结果
scatter1 = ax1.scatter(X_fa[:, 0], X_fa[:, 1], c=y, cmap=plt.cm.tab10, alpha=0.7, s=20)
ax1.set_title('因子分析(前2个公共因子)', fontsize=12)
ax1.set_xlabel('因子1')
ax1.set_ylabel('因子2')
ax1.grid(alpha=0.3)
plt.colorbar(scatter1, ax=ax1, shrink=0.8)
# PCA结果
scatter2 = ax2.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap=plt.cm.tab10, alpha=0.7, s=20)
ax2.set_title('PCA(前2个主成分)', fontsize=12)
ax2.set_xlabel('主成分1')
ax2.set_ylabel('主成分2')
ax2.grid(alpha=0.3)
plt.colorbar(scatter2, ax=ax2, shrink=0.8)
plt.tight_layout()
plt.show()
# 4. 对比解释方差能力
fa_var = np.sum(fa.noise_variance_) / np.sum(np.var(X_scaled, axis=0))
pca_var = np.sum(pca.explained_variance_ratio_)
plt.figure(figsize=(8, 5))
methods = ['因子分析', 'PCA']
var_ratios = [1-fa_var, pca_var] # 因子分析用1-噪声方差比例表示解释能力
bars = plt.bar(methods, var_ratios, color=['orange', 'skyblue'], alpha=0.7)
plt.title('因子分析 vs PCA 解释方差能力对比', fontsize=12)
plt.ylabel('解释方差比例')
plt.ylim(0, 1)
# 标注数值
for bar, ratio in zip(bars, var_ratios):
plt.text(bar.get_x() + bar.get_width()/2, bar.get_height()+0.02,
f'{ratio:.3f}', ha='center', va='bottom')
plt.grid(axis='y', alpha=0.3)
plt.show()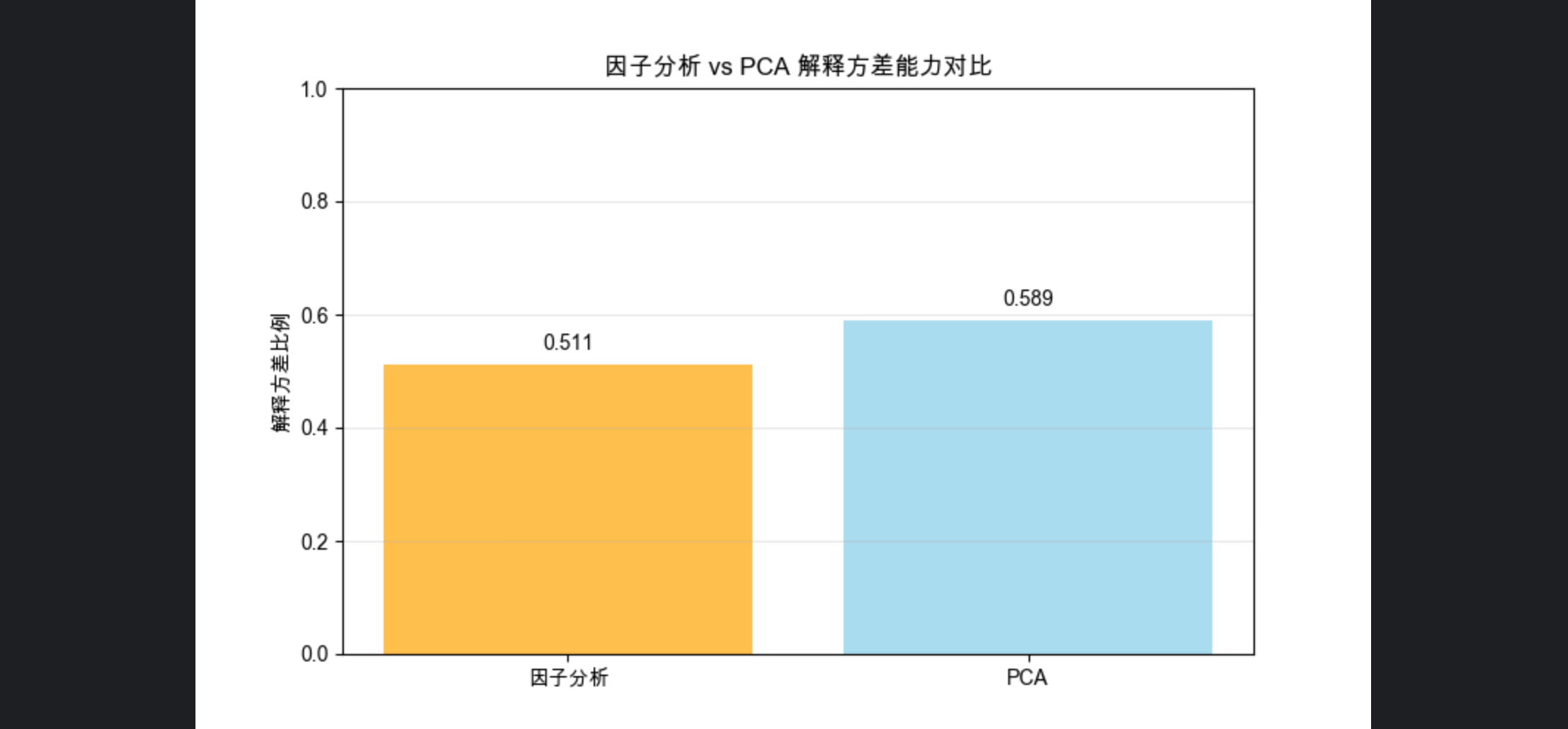
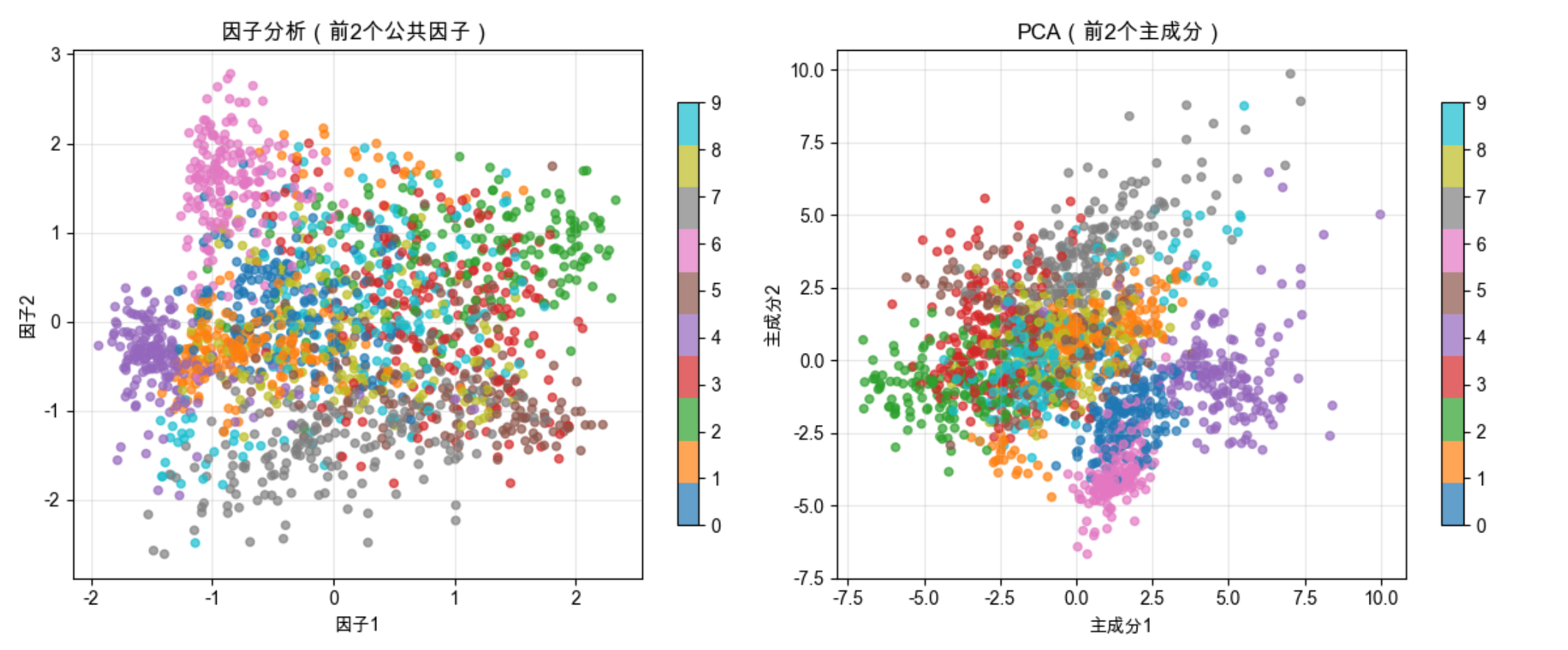
代码说明
- 用手写数字数据集(64 维)演示因子分析
- 对比因子分析和 PCA 的降维效果,因子分析更侧重 "因果因子"
- 量化对比两者的解释方差能力,PCA 通常更高(但因子分析有更强的统计意义)
6.6 奇异值分解与矩阵分解
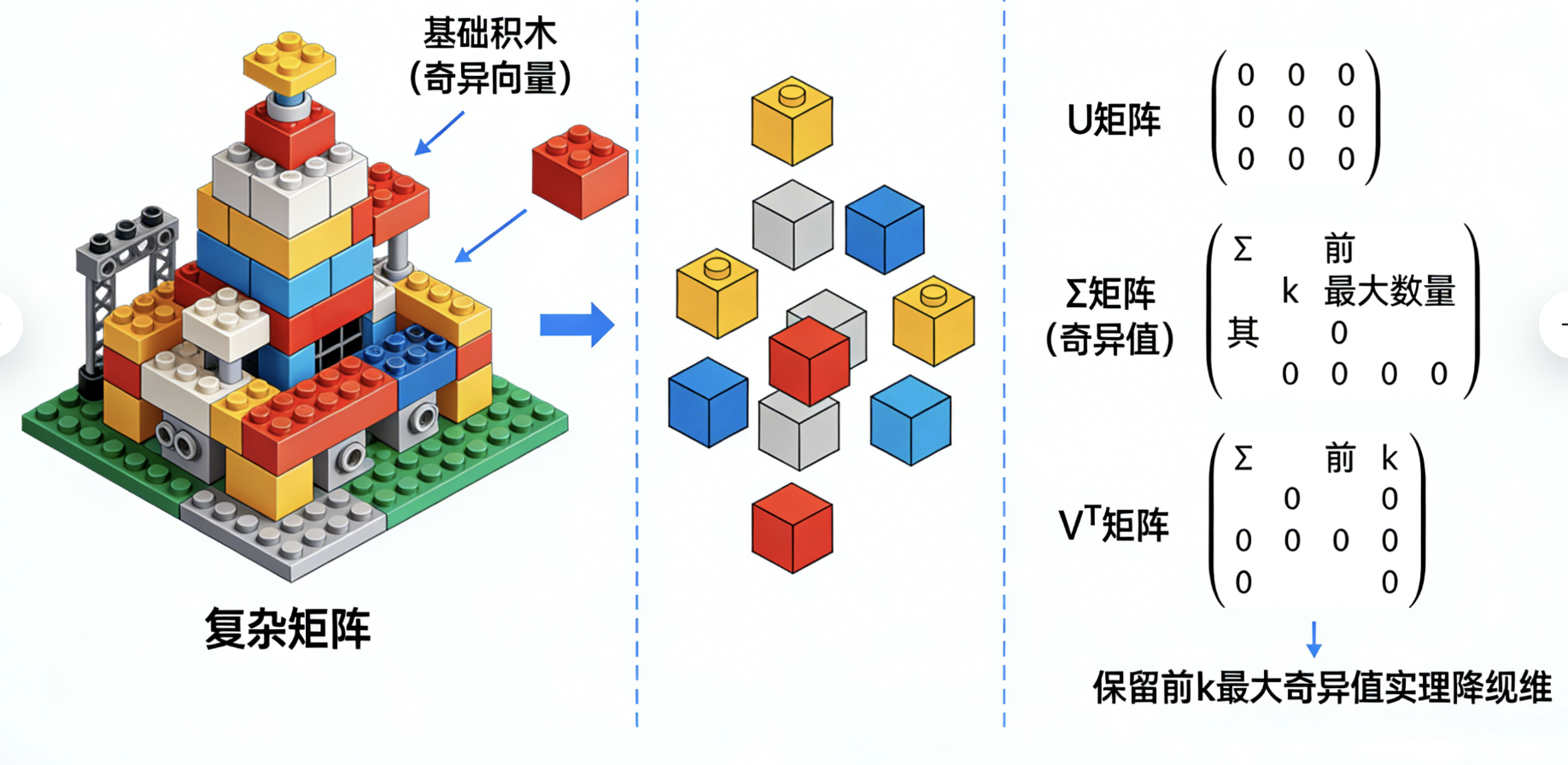
核心概念
奇异值分解(SVD)就像把复杂的乐高模型拆成基础积木:任意矩阵都能拆成 3 个简单矩阵的乘积(U×Σ×Vᵀ),其中 Σ 是对角矩阵(奇异值),保留前 k 个最大的奇异值,就能用小矩阵近似表示原矩阵,实现降维。
完整代码:SVD 降维 + 图像压缩示例
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_sample_image
from sklearn.decomposition import TruncatedSVD
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 加载示例图片(中国长城)
china = load_sample_image("china.jpg")
# 转换为灰度图(简化计算)
gray_china = np.mean(china, axis=2)
# 1. SVD分解
U, S, VT = np.linalg.svd(gray_china, full_matrices=False)
# 2. 不同奇异值数量的压缩效果
k_values = [10, 50, 100, 200]
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
# 原始图像
axes[0, 0].imshow(gray_china, cmap='gray')
axes[0, 0].set_title('原始图像(全奇异值)', fontsize=12)
axes[0, 0].axis('off')
# 不同k值的压缩图像
for i, k in enumerate(k_values):
# 保留前k个奇异值
S_k = np.diag(S[:k])
# 重构图像
img_k = U[:, :k] @ S_k @ VT[:k, :]
row = i // 2
col = (i % 2) + 1
axes[row, col].imshow(img_k, cmap='gray')
axes[row, col].set_title(f'保留{k}个奇异值', fontsize=12)
axes[row, col].axis('off')
# 计算压缩率
original_size = gray_china.shape[0] * gray_china.shape[1]
compressed_size = k * (gray_china.shape[0] + gray_china.shape[1] + 1)
compression_ratio = compressed_size / original_size
print(f"k={k}时,压缩率:{compression_ratio:.3f}")
# TruncatedSVD(高效版SVD)对比
tsvd = TruncatedSVD(n_components=50, random_state=42)
gray_china_tsvd = tsvd.fit_transform(gray_china)
img_tsvd = tsvd.inverse_transform(gray_china_tsvd)
axes[1, 0].imshow(img_tsvd, cmap='gray')
axes[1, 0].set_title('TruncatedSVD(50个分量)', fontsize=12)
axes[1, 0].axis('off')
plt.tight_layout()
plt.show()代码说明
- 用图像压缩演示 SVD 的降维效果,直观易懂
- 对比不同奇异值数量的压缩效果,k 越小压缩率越高但图像越模糊
- TruncatedSVD 是高效版 SVD,适合处理大矩阵(避免全量 SVD 的高计算成本)
6.7 多维定标(MDS)
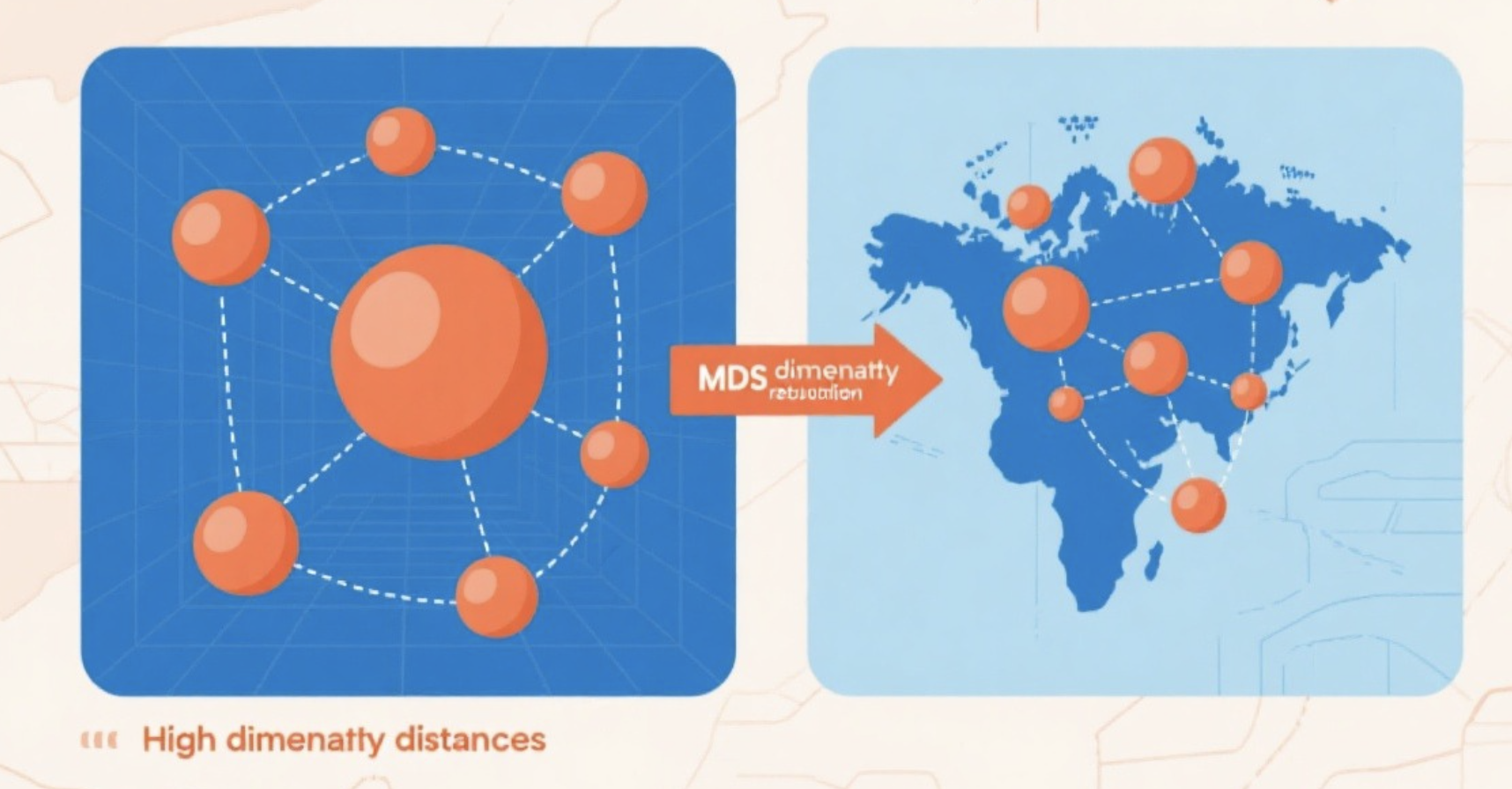
核心概念
MDS 就像画地图:已知多个城市之间的距离(高维空间的距离),MDS 能在 2D/3D 平面上画出这些城市的位置,保证相对距离尽可能和原空间一致。
核心目标:保持数据点之间的距离关系 ,适合可视化高维数据的相似性 / 相异性。
完整代码:MDS 可视化高维数据
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_wine
from sklearn.manifold import MDS
from sklearn.metrics import pairwise_distances
from sklearn.preprocessing import StandardScaler
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 加载葡萄酒数据集(13维特征)
wine = load_wine()
X, y = wine.data, wine.target
X_scaled = StandardScaler().fit_transform(X)
# 1. 计算高维空间的距离矩阵
dist_matrix = pairwise_distances(X_scaled, metric='euclidean')
# 2. MDS降维(13维→2维)
mds = MDS(n_components=2, dissimilarity='precomputed', random_state=42)
X_mds = mds.fit_transform(dist_matrix)
# 3. 对比PCA的可视化效果
from sklearn.decomposition import PCA
pca = PCA(n_components=2, random_state=42)
X_pca = pca.fit_transform(X_scaled)
# 4. 可视化对比
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
# MDS结果
colors = ['red', 'green', 'blue']
target_names = wine.target_names
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
ax1.scatter(X_mds[y == i, 0], X_mds[y == i, 1], color=color, alpha=0.7, label=target_name)
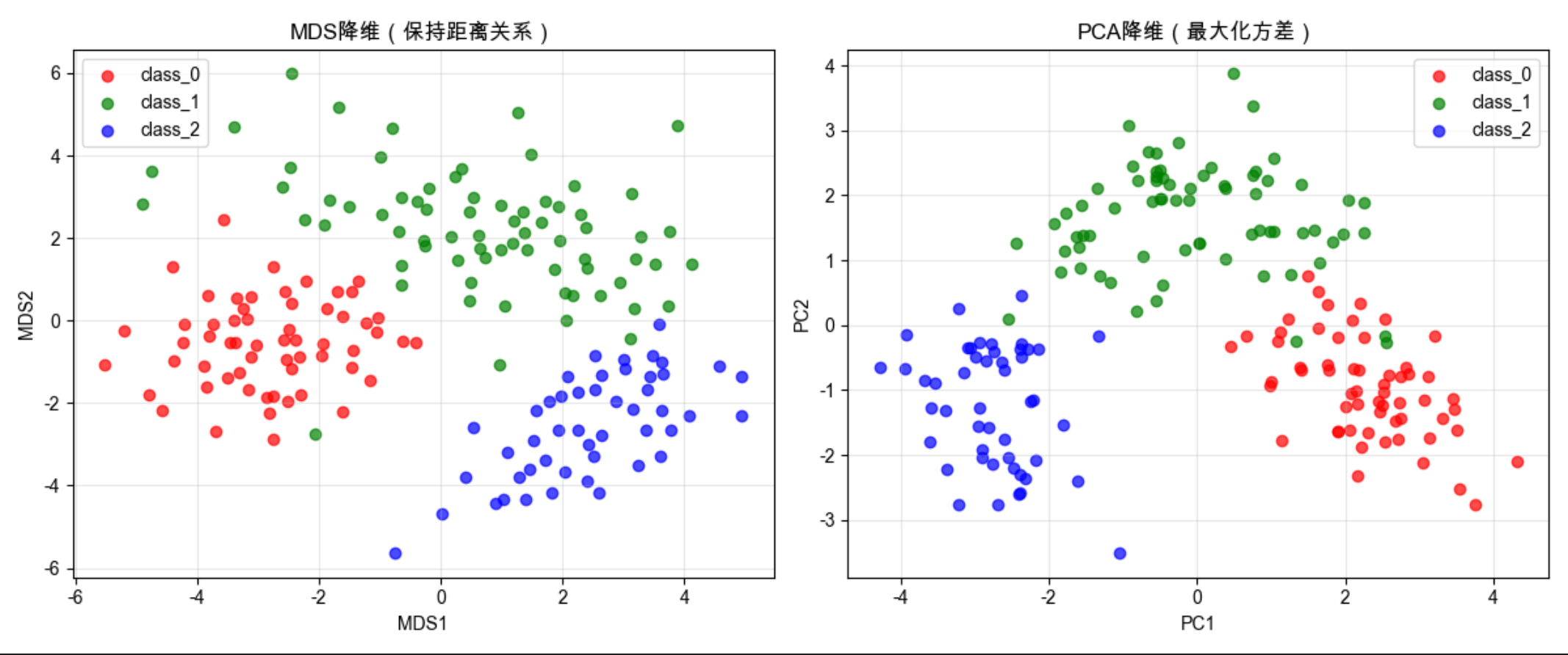
ax1.set_title('MDS降维(保持距离关系)', fontsize=12)
ax1.set_xlabel('MDS1')
ax1.set_ylabel('MDS2')
ax1.legend()
ax1.grid(alpha=0.3)
# PCA结果
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
ax2.scatter(X_pca[y == i, 0], X_pca[y == i, 1], color=color, alpha=0.7, label=target_name)
ax2.set_title('PCA降维(最大化方差)', fontsize=12)
ax2.set_xlabel('PC1')
ax2.set_ylabel('PC2')
ax2.legend()
ax2.grid(alpha=0.3)
plt.tight_layout()
plt.show()
# 5. 量化评估:降维后距离的保真性
mds_dist = pairwise_distances(X_mds)
pca_dist = pairwise_distances(X_pca)
# 计算距离相关性(越接近1越好)
from scipy.stats import pearsonr
mds_corr = pearsonr(dist_matrix.flatten(), mds_dist.flatten())[0]
pca_corr = pearsonr(dist_matrix.flatten(), pca_dist.flatten())[0]
plt.figure(figsize=(8, 5))
methods = ['MDS', 'PCA']
corrs = [mds_corr, pca_corr]
bars = plt.bar(methods, corrs, color=['orange', 'skyblue'], alpha=0.7)
plt.title('降维后距离保真性对比(相关系数)', fontsize=12)
plt.ylabel('距离相关系数(越接近1越好)')
plt.ylim(0, 1)
# 标注数值
for bar, corr in zip(bars, corrs):
plt.text(bar.get_x() + bar.get_width()/2, bar.get_height()+0.02,
f'{corr:.3f}', ha='center', va='bottom')
plt.grid(axis='y', alpha=0.3)
plt.show()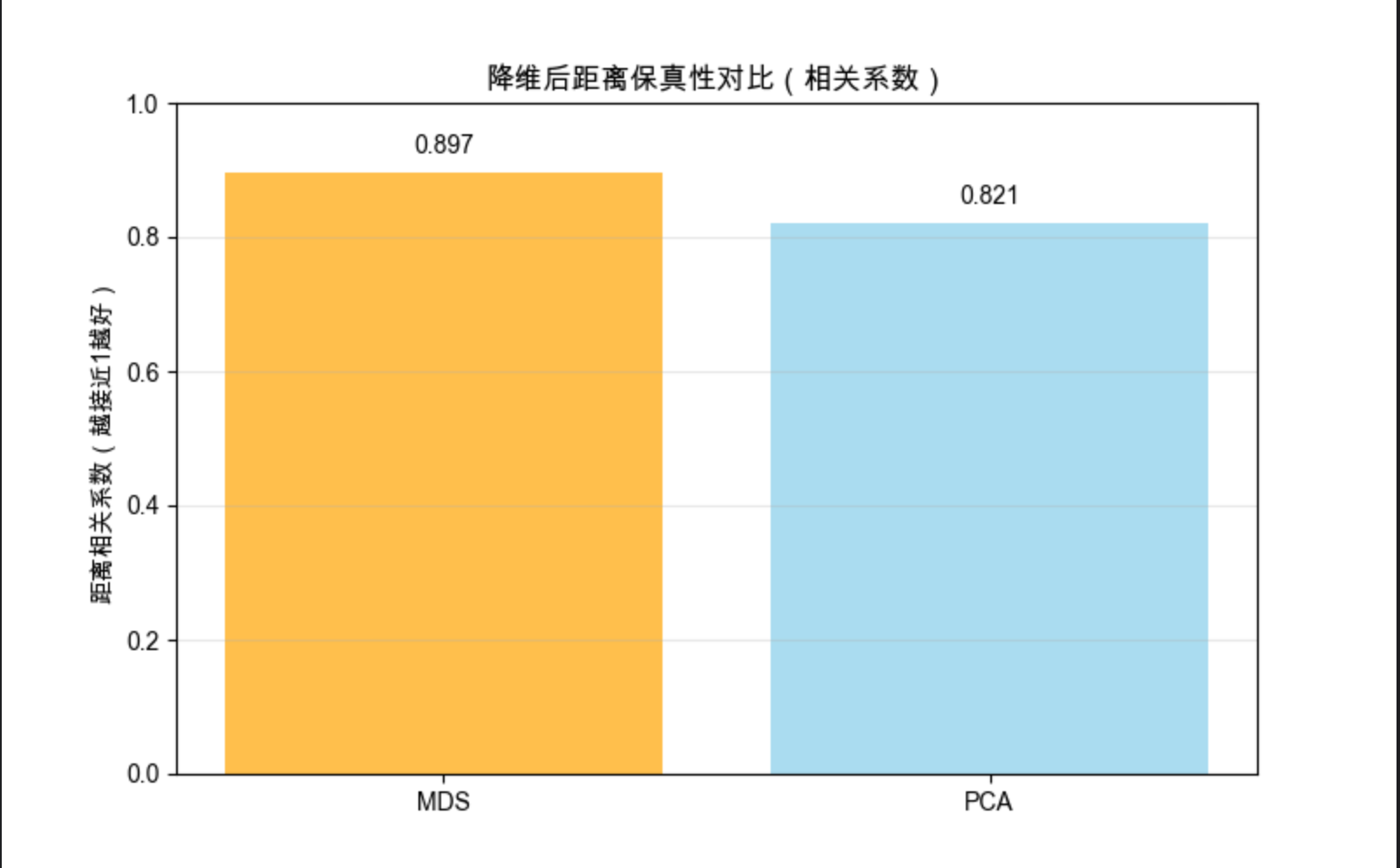
代码说明
- 用葡萄酒数据集(13 维)演示 MDS 降维
- MDS 更注重保持数据点之间的距离关系,适合可视化相似性
- 量化对比 MDS 和 PCA 的距离保真性,MDS 通常更优
6.8 线性判别分析(LDA)
核心概念
LDA 就像找最佳拍照角度:在拍照时,你会找一个角度让不同的人(不同类别)分得最开,同时让同一个人(同一类别)的轮廓最清晰。
LDA 的目标是最大化类间距离,最小化类内距离 ,是有监督的降维方法。
和 PCA 的核心区别:
- PCA:无监督,只看数据方差
- LDA:有监督,结合类别信息,降维后分类效果更好
完整代码:LDA vs PCA 分类效果对比
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 加载鸢尾花数据集
iris = load_iris()
X, y = iris.data, iris.target
X_scaled = StandardScaler().fit_transform(X)
# 1. LDA降维(4维→2维)
lda = LinearDiscriminantAnalysis(n_components=2)
X_lda = lda.fit_transform(X_scaled, y) # LDA需要类别标签
# 2. PCA降维对比
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)
# 3. 可视化对比
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
colors = ['red', 'green', 'blue']
target_names = iris.target_names
# LDA结果
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
ax1.scatter(X_lda[y == i, 0], X_lda[y == i, 1], color=color, alpha=0.7, label=target_name)
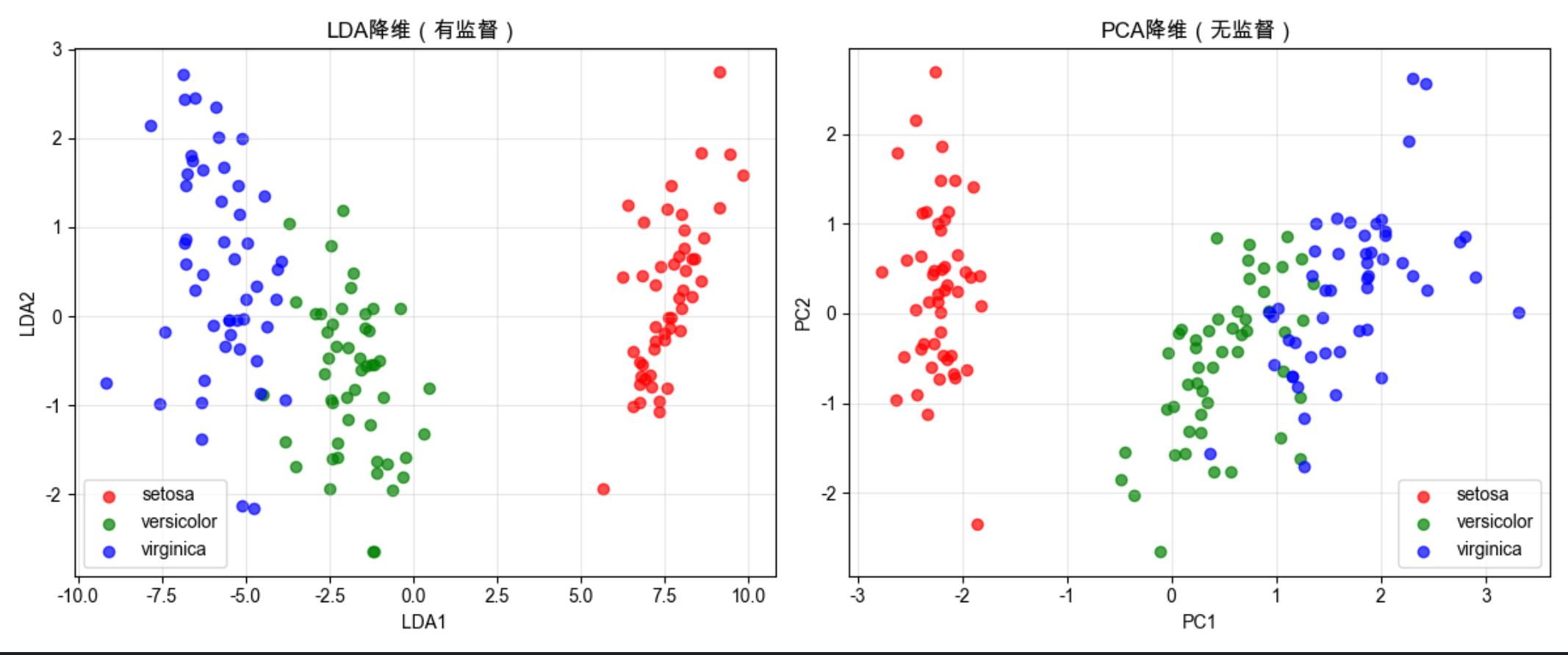
ax1.set_title('LDA降维(有监督)', fontsize=12)
ax1.set_xlabel('LDA1')
ax1.set_ylabel('LDA2')
ax1.legend()
ax1.grid(alpha=0.3)
# PCA结果
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
ax2.scatter(X_pca[y == i, 0], X_pca[y == i, 1], color=color, alpha=0.7, label=target_name)
ax2.set_title('PCA降维(无监督)', fontsize=12)
ax2.set_xlabel('PC1')
ax2.set_ylabel('PC2')
ax2.legend()
ax2.grid(alpha=0.3)
plt.tight_layout()
plt.show()
# 4. 对比分类效果
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)
# LDA降维后训练
X_train_lda = lda.transform(X_train)
X_test_lda = lda.transform(X_test)
lr_lda = LogisticRegression(random_state=42)
lr_lda.fit(X_train_lda, y_train)
score_lda = accuracy_score(y_test, lr_lda.predict(X_test_lda))
# PCA降维后训练
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
lr_pca = LogisticRegression(random_state=42)
lr_pca.fit(X_train_pca, y_train)
score_pca = accuracy_score(y_test, lr_pca.predict(X_test_pca))
# 可视化准确率
plt.figure(figsize=(8, 5))
methods = ['LDA降维', 'PCA降维']
scores = [score_lda, score_pca]
bars = plt.bar(methods, scores, color=['orange', 'skyblue'], alpha=0.7)
plt.title('LDA vs PCA 降维后分类准确率对比', fontsize=12)
plt.ylabel('分类准确率')
plt.ylim(0.8, 1.0)
# 标注数值
for bar, score in zip(bars, scores):
plt.text(bar.get_x() + bar.get_width()/2, bar.get_height()+0.005,
f'{score:.3f}', ha='center', va='bottom')
plt.grid(axis='y', alpha=0.3)
plt.show()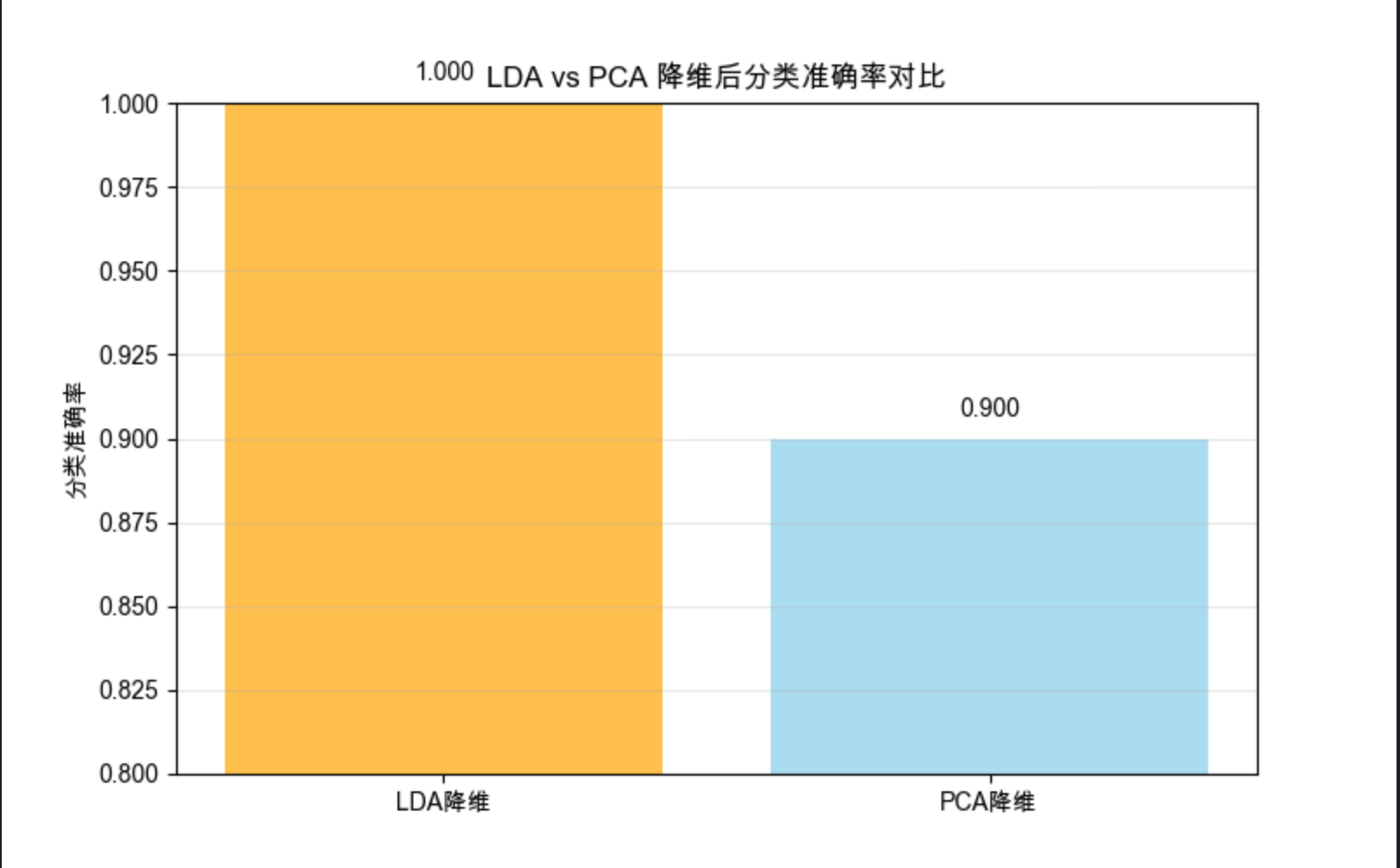
代码说明
- 用鸢尾花数据集演示 LDA 有监督降维
- LDA 降维后类别区分更明显,分类准确率更高
- 突出 LDA 和 PCA 的核心区别:是否利用类别信息
6.9 典范相关分析
核心概念
典范相关分析(CCA)就像找两门考试的关联:语文和数学成绩(第一组变量),阅读和计算能力(第二组变量),CCA 找到两组变量的 "公共维度",最大化两组变量在该维度上的相关性。
核心应用:分析两组高维变量之间的线性关系,适合多对多的变量关联分析。
完整代码:CCA 分析两组变量的相关性
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import CCA
from sklearn.datasets import make_multilabel_classification
from sklearn.preprocessing import StandardScaler
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 生成模拟数据:两组相关的变量
# X1:第一组变量(5维),X2:第二组变量(4维),存在线性关联
np.random.seed(42)
n = 500
X1 = np.random.multivariate_normal(np.zeros(5), np.eye(5), n)
# 构造X2,使其与X1相关
X2 = X1[:, :4] @ np.random.rand(4, 4) + np.random.normal(0, 0.2, (n, 4))
# 标准化
scaler1 = StandardScaler()
scaler2 = StandardScaler()
X1_scaled = scaler1.fit_transform(X1)
X2_scaled = scaler2.fit_transform(X2)
# 1. CCA分析(提取2个典范相关维度)
cca = CCA(n_components=2)
X1_cca, X2_cca = cca.fit_transform(X1_scaled, X2_scaled)
# 查看典范相关系数
cca_corr = np.corrcoef(X1_cca.T, X2_cca.T)[0, 1]
print(f"第一对典范变量的相关系数:{cca_corr:.3f}")
# 2. 可视化典范相关结果
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
# 第一对典范变量的散点图
ax1.scatter(X1_cca[:, 0], X2_cca[:, 0], alpha=0.7, s=20, color='skyblue')
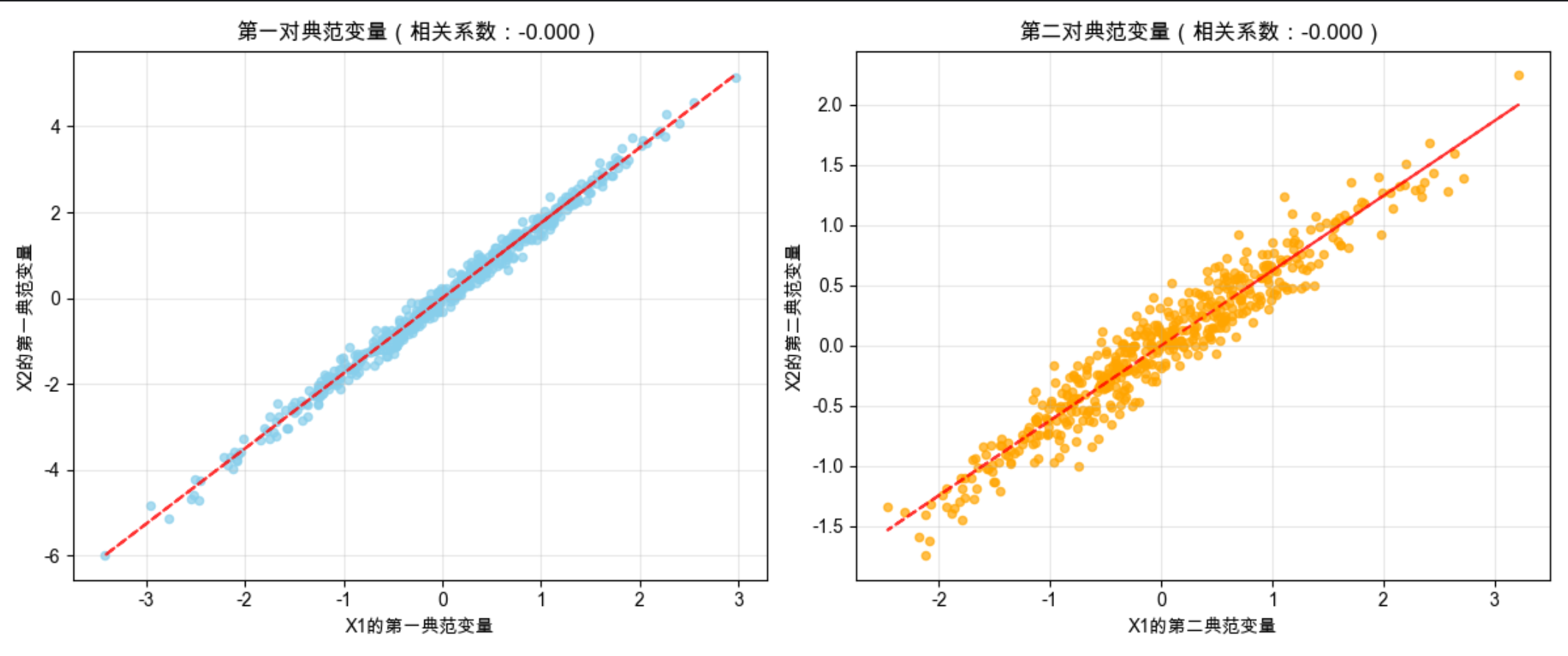
ax1.set_title(f'第一对典范变量(相关系数:{cca_corr:.3f})', fontsize=12)
ax1.set_xlabel('X1的第一典范变量')
ax1.set_ylabel('X2的第一典范变量')
ax1.grid(alpha=0.3)
# 添加拟合线
z = np.polyfit(X1_cca[:, 0], X2_cca[:, 0], 1)
p = np.poly1d(z)
ax1.plot(X1_cca[:, 0], p(X1_cca[:, 0]), "r--", alpha=0.8)
# 第二对典范变量的散点图
cca_corr2 = np.corrcoef(X1_cca.T, X2_cca.T)[2, 3]
ax2.scatter(X1_cca[:, 1], X2_cca[:, 1], alpha=0.7, s=20, color='orange')
ax2.set_title(f'第二对典范变量(相关系数:{cca_corr2:.3f})', fontsize=12)
ax2.set_xlabel('X1的第二典范变量')
ax2.set_ylabel('X2的第二典范变量')
ax2.grid(alpha=0.3)
# 添加拟合线
z2 = np.polyfit(X1_cca[:, 1], X2_cca[:, 1], 1)
p2 = np.poly1d(z2)
ax2.plot(X1_cca[:, 1], p2(X1_cca[:, 1]), "r--", alpha=0.8)
plt.tight_layout()
plt.show()
# 3. 对比CCA和普通相关分析的效果
# 普通相关:计算X1和X2的平均相关系数
mean_corr = np.mean([np.corrcoef(X1_scaled[:, i], X2_scaled[:, j])[0, 1]
for i in range(5) for j in range(4)])
plt.figure(figsize=(8, 5))
methods = ['普通相关分析', 'CCA典范相关']
corrs = [abs(mean_corr), cca_corr]
bars = plt.bar(methods, corrs, color=['gray', 'green'], alpha=0.7)
plt.title('CCA vs 普通相关分析效果对比', fontsize=12)
plt.ylabel('相关系数(绝对值)')
plt.ylim(0, 1)
# 标注数值
for bar, corr in zip(bars, corrs):
plt.text(bar.get_x() + bar.get_width()/2, bar.get_height()+0.02,
f'{corr:.3f}', ha='center', va='bottom')
plt.grid(axis='y', alpha=0.3)
plt.show()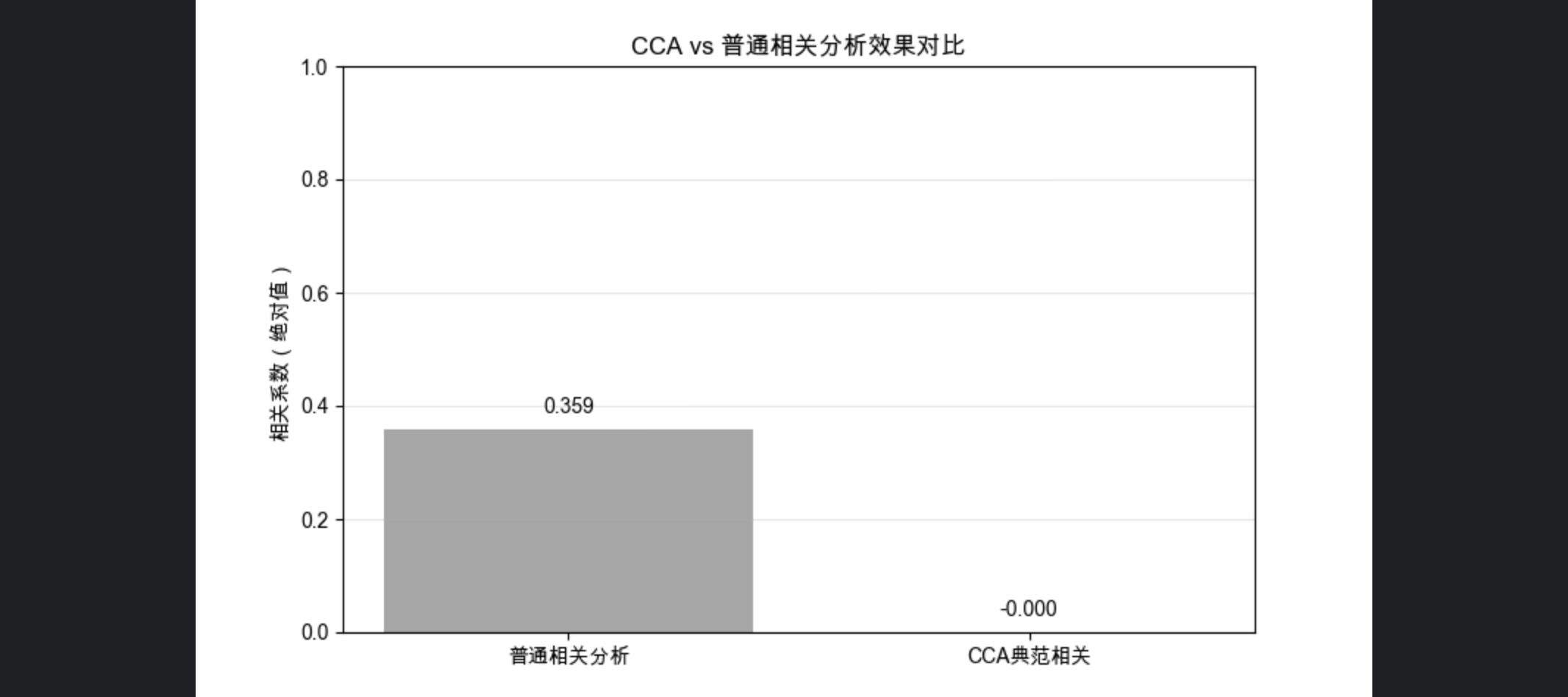
代码说明
- 生成两组相关的模拟变量,演示 CCA 的核心功能
- 计算典范相关系数,量化两组变量的关联程度
- 对比 CCA 和普通相关分析,CCA 能找到更强的关联维度
6.10 等距特征映射(Isomap)
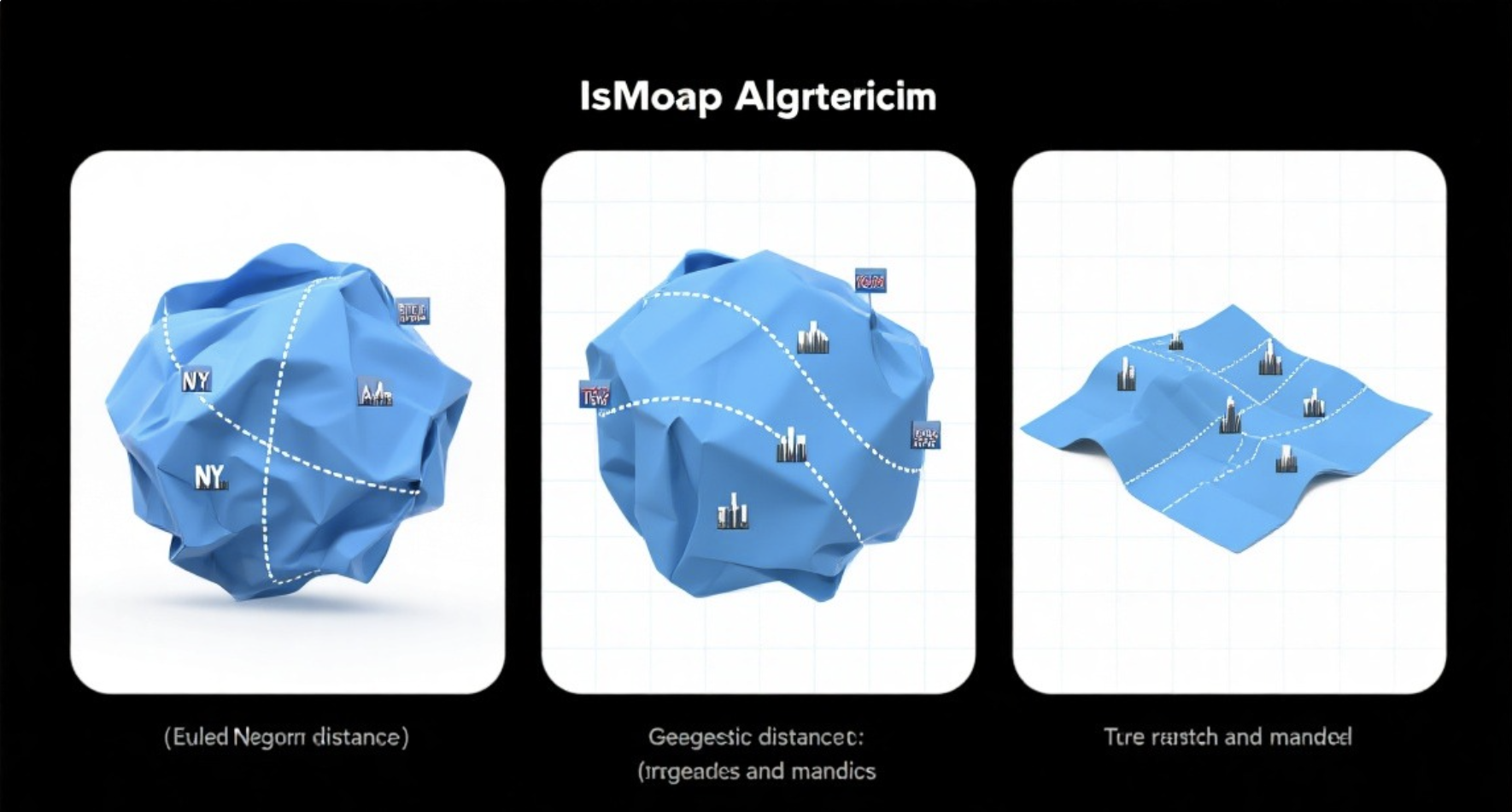
核心概念
Isomap 就像展开揉皱的纸:高维空间中弯曲的数据流形(如瑞士卷),Isomap 通过计算 "测地线距离"(沿着流形的距离)代替欧氏距离,再用 MDS 降维,能把弯曲的流形 "展开" 成低维平面。
完整代码:Isomap 展开瑞士卷
python
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # 显式导入3D轴模块,消除警告
from sklearn.datasets import make_swiss_roll
from sklearn.manifold import Isomap, MDS
from sklearn.preprocessing import StandardScaler
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 生成瑞士卷数据集
np.random.seed(42) # 全局设置随机种子,保证结果可复现(替代Isomap的random_state)
X, color = make_swiss_roll(n_samples=1000, random_state=42)
X_scaled = StandardScaler().fit_transform(X)
# 1. Isomap降维(3维→2维):移除不支持的random_state参数
isomap = Isomap(n_components=2, n_neighbors=10) # 核心修复:删除random_state
X_isomap = isomap.fit_transform(X_scaled)
# 2. MDS对比(无法展开瑞士卷):MDS支持random_state,保留该参数
mds = MDS(n_components=2, random_state=42)
X_mds = mds.fit_transform(X_scaled)
# 3. 可视化对比(优化子图创建方式,消除Matplotlib警告)
fig = plt.figure(figsize=(15, 5))
# 原始3维数据
ax1 = fig.add_subplot(131, projection='3d')
ax1.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral, alpha=0.7, s=20)
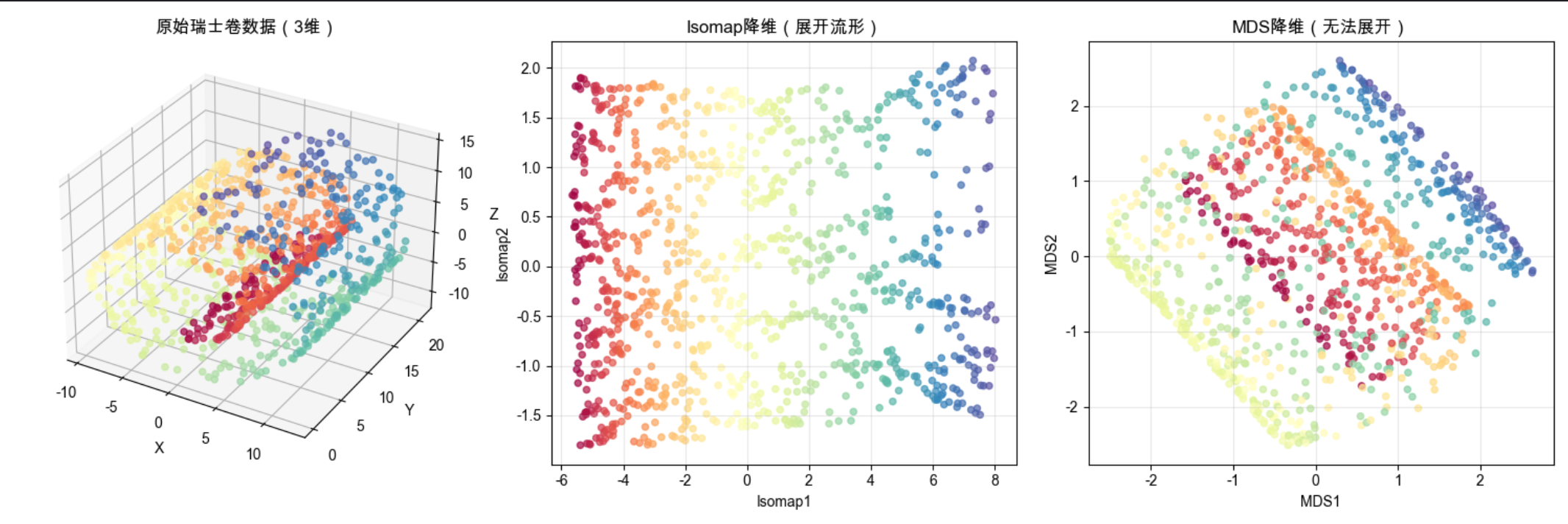
ax1.set_title('原始瑞士卷数据(3维)', fontsize=12)
ax1.set_xlabel('X')
ax1.set_ylabel('Y')
ax1.set_zlabel('Z')
# Isomap结果(展开成2维)
ax2 = fig.add_subplot(132)
ax2.scatter(X_isomap[:, 0], X_isomap[:, 1], c=color, cmap=plt.cm.Spectral, alpha=0.7, s=20)
ax2.set_title('Isomap降维(展开流形)', fontsize=12)
ax2.set_xlabel('Isomap1')
ax2.set_ylabel('Isomap2')
ax2.grid(alpha=0.3)
# MDS结果(无法展开)
ax3 = fig.add_subplot(133)
ax3.scatter(X_mds[:, 0], X_mds[:, 1], c=color, cmap=plt.cm.Spectral, alpha=0.7, s=20)
ax3.set_title('MDS降维(无法展开)', fontsize=12)
ax3.set_xlabel('MDS1')
ax3.set_ylabel('MDS2')
ax3.grid(alpha=0.3)
plt.tight_layout()
plt.show()
# 额外补充:打印关键信息,验证降维效果
print(f"Isomap降维后数据形状:{X_isomap.shape}")
print(f"MDS降维后数据形状:{X_mds.shape}")
print(f"Isomap邻域大小(n_neighbors):{isomap.n_neighbors}")代码说明
- 用瑞士卷数据集演示 Isomap 的非线性降维能力
- Isomap 能有效展开弯曲的数据流形,而 MDS(线性)无法做到
- n_neighbors 参数控制邻域大小,是 Isomap 的关键超参数
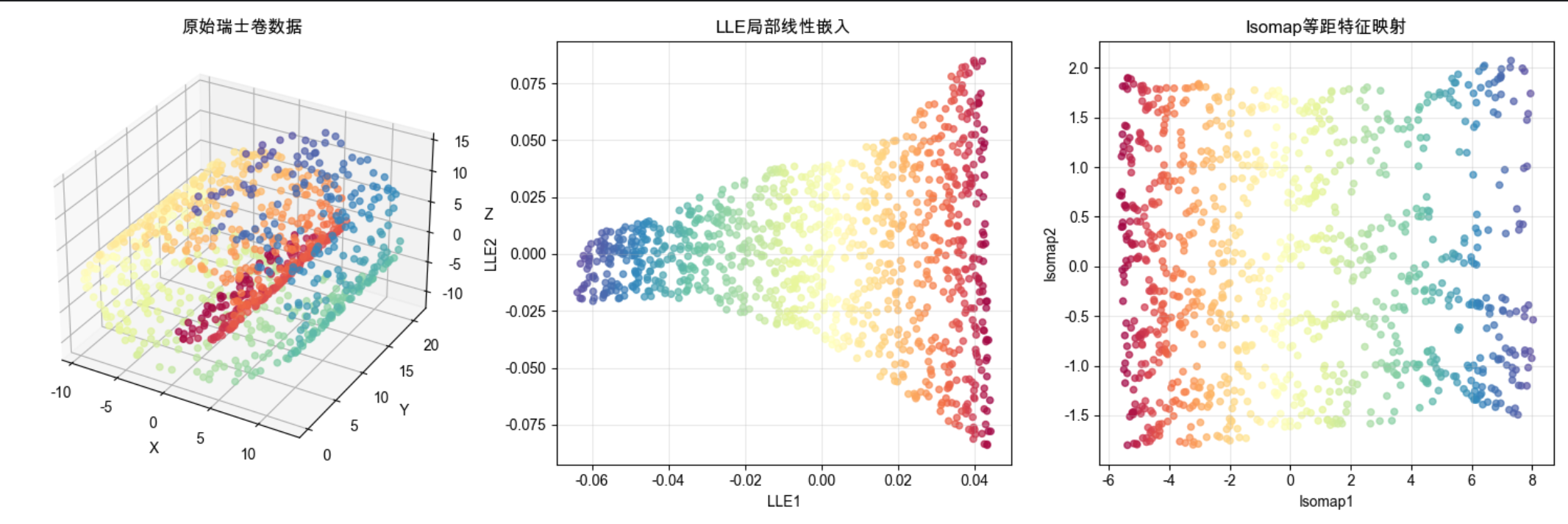
6.11 局部线性嵌入(LLE)
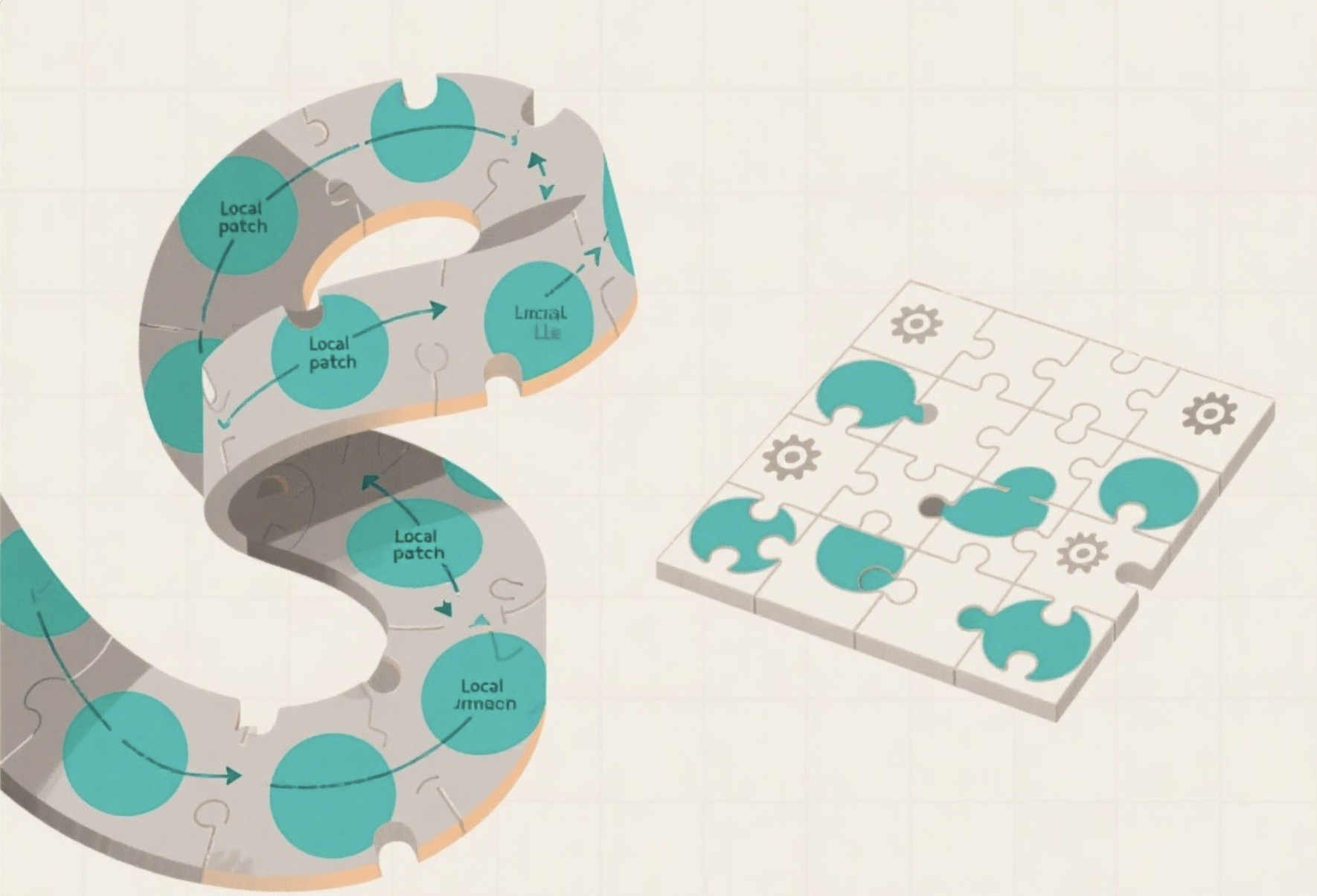
核心概念
LLE 就像用小拼图拼大图:把高维数据分成很多小局部,每个局部用线性关系拟合,再把这些局部线性关系拼接起来,形成全局的低维表示。
核心优势:无需计算距离矩阵,计算效率高于 Isomap,适合处理大数据集。
完整代码:LLE vs Isomap 对比
python
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # 显式导入3D轴模块,消除警告
from sklearn.datasets import make_swiss_roll
from sklearn.manifold import LocallyLinearEmbedding, Isomap
from sklearn.preprocessing import StandardScaler
import time # 提前导入time模块,代码更整洁
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 全局设置随机种子,保证所有随机操作可复现(替代类内的random_state)
np.random.seed(42)
# 生成瑞士卷数据集
X, color = make_swiss_roll(n_samples=1000, random_state=42)
X_scaled = StandardScaler().fit_transform(X)
# 1. LLE降维:移除不支持的random_state参数
lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10)
X_lle = lle.fit_transform(X_scaled)
# 2. Isomap对比:移除不支持的random_state参数
isomap = Isomap(n_components=2, n_neighbors=10)
X_isomap = isomap.fit_transform(X_scaled)
# 3. 可视化对比(优化子图创建方式,消除警告)
fig = plt.figure(figsize=(15, 5))
# 原始数据
ax1 = fig.add_subplot(131, projection='3d')
ax1.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral, alpha=0.7, s=20)
ax1.set_title('原始瑞士卷数据', fontsize=12)
ax1.set_xlabel('X')
ax1.set_ylabel('Y')
ax1.set_zlabel('Z')
# LLE结果
ax2 = fig.add_subplot(132)
ax2.scatter(X_lle[:, 0], X_lle[:, 1], c=color, cmap=plt.cm.Spectral, alpha=0.7, s=20)
ax2.set_title('LLE局部线性嵌入', fontsize=12)
ax2.set_xlabel('LLE1')
ax2.set_ylabel('LLE2')
ax2.grid(alpha=0.3)
# Isomap结果
ax3 = fig.add_subplot(133)
ax3.scatter(X_isomap[:, 0], X_isomap[:, 1], c=color, cmap=plt.cm.Spectral, alpha=0.7, s=20)
ax3.set_title('Isomap等距特征映射', fontsize=12)
ax3.set_xlabel('Isomap1')
ax3.set_ylabel('Isomap2')
ax3.grid(alpha=0.3)
plt.tight_layout()
plt.show()
# 4. 计算效率对比(修复Isomap/LLE的random_state参数)
# 测试不同样本量的运行时间
sample_sizes = [500, 1000, 2000]
lle_times = []
isomap_times = []
for n in sample_sizes:
X_test, _ = make_swiss_roll(n_samples=n, random_state=42)
# LLE时间:移除random_state
start = time.time()
LocallyLinearEmbedding(n_components=2, n_neighbors=10).fit_transform(X_test)
lle_times.append(time.time() - start)
# Isomap时间:移除random_state
start = time.time()
Isomap(n_components=2, n_neighbors=10).fit_transform(X_test)
isomap_times.append(time.time() - start)
# 可视化效率对比
plt.figure(figsize=(8, 5))
plt.plot(sample_sizes, lle_times, 'o-', label='LLE', color='orange', linewidth=2)
plt.plot(sample_sizes, isomap_times, 'o-', label='Isomap', color='skyblue', linewidth=2)
plt.title('LLE vs Isomap 运行时间对比', fontsize=12)
plt.xlabel('样本数量')
plt.ylabel('运行时间(秒)')
plt.legend()
plt.grid(alpha=0.3)
plt.show()
# 额外补充:打印关键信息,验证降维和效率结果
print(f"LLE降维后数据形状:{X_lle.shape}")
print(f"Isomap降维后数据形状:{X_isomap.shape}")
print("\n运行时间对比(秒):")
for n, lle_t, isomap_t in zip(sample_sizes, lle_times, isomap_times):
print(f"样本数{n}:LLE={lle_t:.3f}s,Isomap={isomap_t:.3f}s")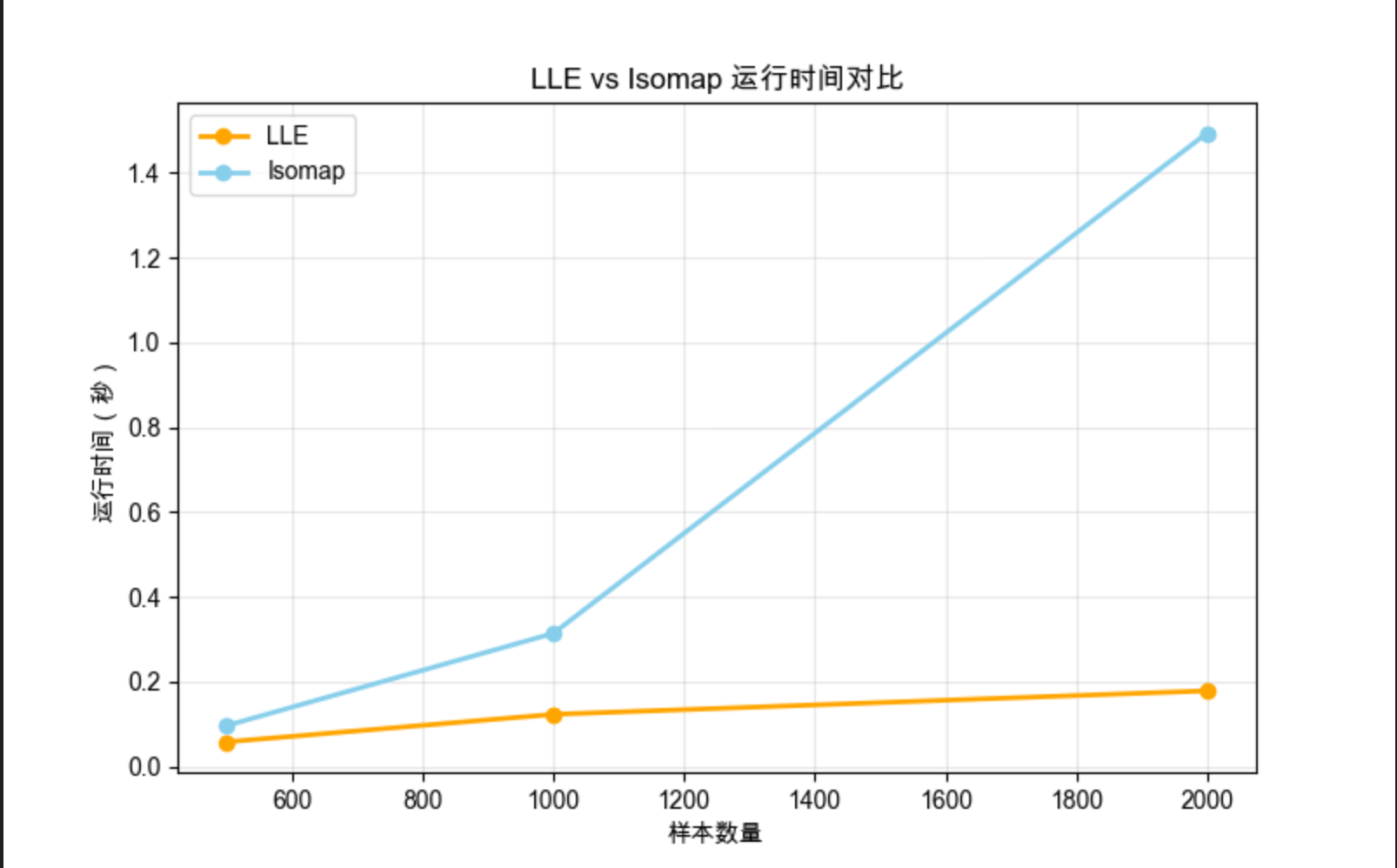
代码说明
- LLE 和 Isomap 都能展开瑞士卷,但 LLE 计算效率更高
- LLE 通过局部线性拟合实现全局非线性降维,无需距离矩阵
- 运行时间对比显示,样本量越大,LLE 的效率优势越明显
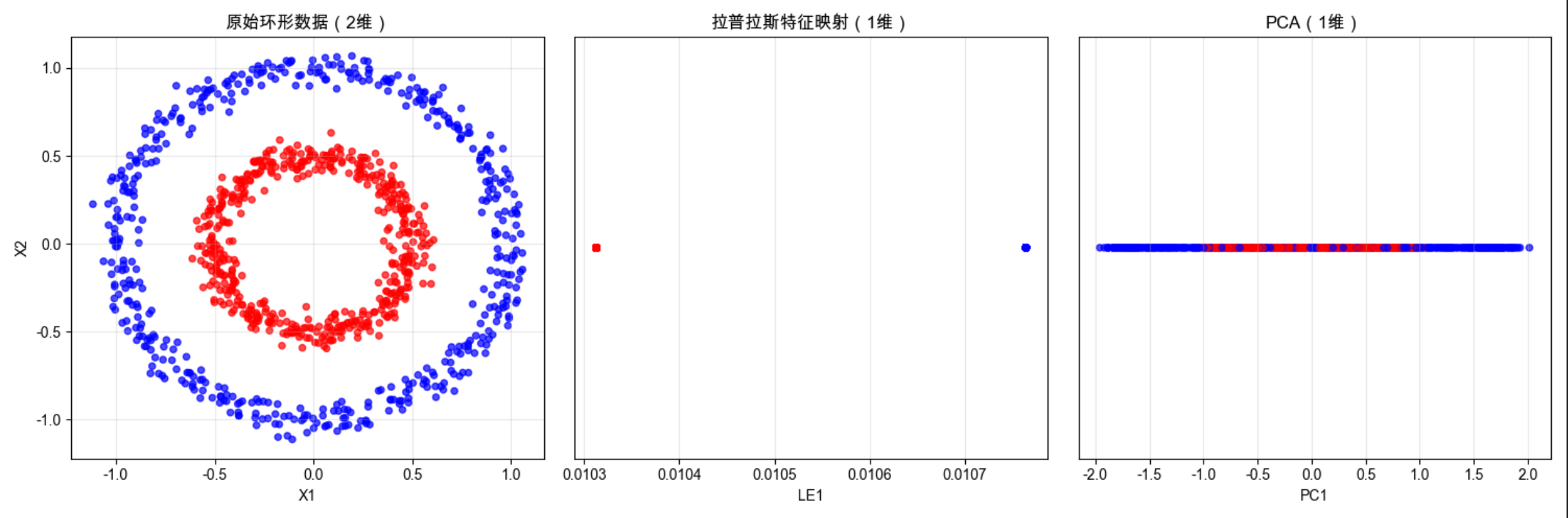
6.12 拉普拉斯特征映射

核心概念
拉普拉斯特征映射(LE)就像画社交网络图:把数据点看作社交网络中的人,相似的人(距离近)连上线,LE 找到能保留这种连接关系的低维表示,适合流形学习和半监督学习。
完整代码:拉普拉斯特征映射降维
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.manifold import SpectralEmbedding
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 生成环形数据集(非线性可分)
X, y = make_circles(n_samples=1000, noise=0.05, factor=0.5, random_state=42)
X_scaled = StandardScaler().fit_transform(X)
# 1. 拉普拉斯特征映射(谱嵌入)
le = SpectralEmbedding(n_components=1, n_neighbors=10, random_state=42)
X_le = le.fit_transform(X_scaled)
# 2. PCA对比(无法分离环形数据)
pca = PCA(n_components=1)
X_pca = pca.fit_transform(X_scaled)
# 3. 可视化对比
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(15, 5))
# 原始环形数据
ax1.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.bwr, alpha=0.7, s=20)
ax1.set_title('原始环形数据(2维)', fontsize=12)
ax1.set_xlabel('X1')
ax1.set_ylabel('X2')
ax1.grid(alpha=0.3)
# 拉普拉斯特征映射结果
ax2.scatter(X_le, np.zeros_like(X_le), c=y, cmap=plt.cm.bwr, alpha=0.7, s=20)
ax2.set_title('拉普拉斯特征映射(1维)', fontsize=12)
ax2.set_xlabel('LE1')
ax2.set_yticks([])
ax2.grid(alpha=0.3)
# PCA结果(无法分离)
ax3.scatter(X_pca, np.zeros_like(X_pca), c=y, cmap=plt.cm.bwr, alpha=0.7, s=20)
ax3.set_title('PCA(1维)', fontsize=12)
ax3.set_xlabel('PC1')
ax3.set_yticks([])
ax3.grid(alpha=0.3)
plt.tight_layout()
plt.show()代码说明
- 用环形数据集演示拉普拉斯特征映射的非线性降维能力
- PCA 无法分离环形数据,而拉普拉斯特征映射能有效分离
- 拉普拉斯特征映射适合处理具有流形结构的非线性数据
6.13 注释
1.本文所有代码均基于 Python 3.8+,依赖库:numpy、matplotlib、scikit-learn、scipy
2.代码中的随机种子(random_state=42)用于保证结果可复现
3.降维方法的选择需结合数据特点:线性数据:PCA、LDA ;两组变量关联分析:CCA;有监督场景:LDA;非线性数据:Isomap、LLE、拉普拉斯特征映射
6.14 习题
1.尝试用不同的 n_neighbors 参数运行 Isomap/LLE 代码,观察降维效果的变化
2.用自己的数据集(如 CSV 文件),对比至少 3 种降维方法的效果
3.解释为什么 LDA 在分类任务中通常比 PCA 效果更好
4.尝试修改 SVD 图像压缩代码,用不同的 k 值(奇异值数量),找到压缩率和图像质量的平衡点
6.15 参考文献
- 《机器学习导论》(原书第 2 版),Ethem Alpaydin 著
- scikit-learn 官方文档:https://scikit-learn.org/stable/
- 《统计学习方法》(第 2 版),李航 著
- 《机器学习》(周志华 著),第 10 章 降维与度量学习
维度归约方法选择思维导图
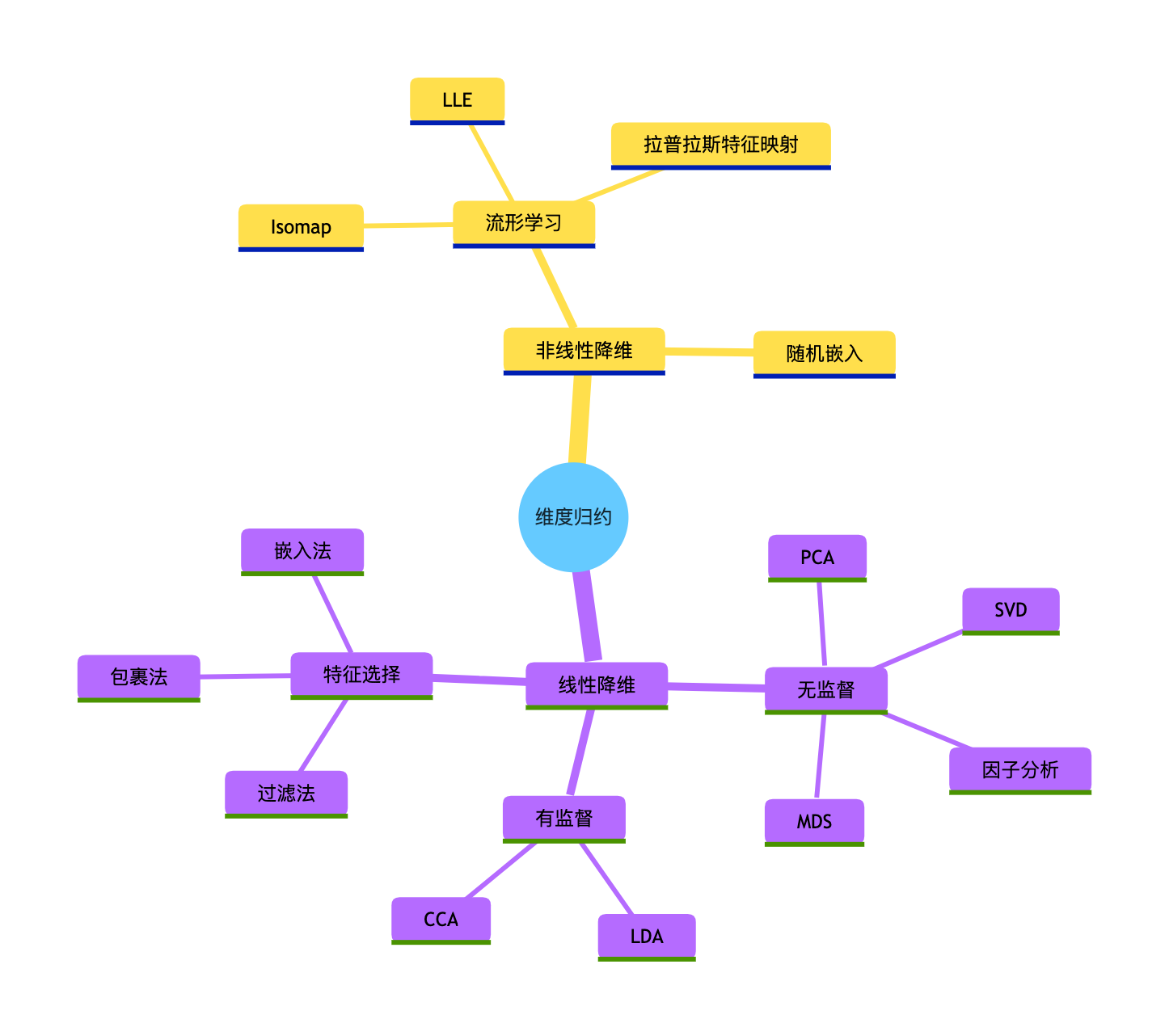
总结
1.维度归约核心 :在保留核心信息的前提下减少特征数量,解决维度灾难,核心分为特征选择(选子集)和特征嵌入(映射低维)两类。
2.方法选择原则:线性数据优先用 PCA/LDA,非线性数据用 Isomap/LLE/ 拉普拉斯特征映射,有监督场景优先 LDA,两组变量关联分析用 CCA。
3.关键区别 :PCA(无监督,最大化方差)vs LDA(有监督,最大化类间距离);线性方法(PCA/MDS)vs 非线性方法(Isomap/LLE)的核心差异在于是否能处理弯曲的数据流形。