122.买卖股票的最佳时机II
题目
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。然而,你可以在 同一天 多次买卖该股票,但要确保你持有的股票不超过一股。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3。
最大总利润为 4 + 3 = 7 。思路
本题首先要清楚两点:
-
只有一只股票!
-
当前只有买股票或者卖股票的操作
想获得利润至少要两天为一个交易单元。
把利润分解为每天为单位的维度,而不是整体去考虑!
那么根据 prices 可以得到每天的利润序列:(prices[i] - prices[i - 1]).....(prices[1] - prices[0])。
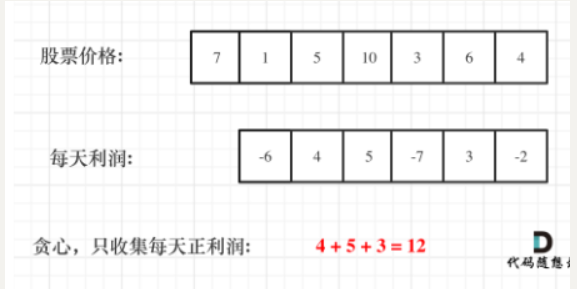
收集正利润的区间,就是股票买卖的区间,而我们只需要关注最终利润,不需要记录区间。
那么只收集正利润就是贪心所贪的地方!
局部最优:收集每天的正利润,全局最优:求得最大利润。
看着难,只要写出每天利润的数组就不难了,代码很短
代码
java
class Solution{
public int maxProfit(int[] prices){
int result=0;
for(int i =1;i<prices.length;i++){
result+=Math.max(prices[i]-prices[i-1],0);
}
return result;
}
}55. 跳跃游戏
题目
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。思路
刚看到本题一开始可能想:当前位置元素如果是 3,我究竟是跳一步呢,还是两步呢,还是三步呢,究竟跳几步才是最优呢?
其实跳几步无所谓,关键在于可跳的覆盖范围!不一定非要明确一次究竟跳几步,每次取最大的跳跃步数,这个就是可以跳跃的覆盖范围。这个范围内,别管是怎么跳的,反正一定可以跳过来。
那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点!
贪心求法就是想要局部最优,比如说一次跳跃,我只想要最远的,如果我最大能跳三步,那走到最远的就是跳三步,不用去想跳一步和两步后序的结果,我每次只要最大的。这就是贪心选择性质,通过局部最优解就能推导全局最优解,不需要等到递归计算出所有子问题的答案才能做选择。
代码
java
class Solution{
public boolean canJump(int[] nums){
int n = nums.length;
int farthest = 0;
//遍历数组的前n-1 个元素,避免处理最后一个元素
for (int i = 0;i<n-1;i++){
//不断计算能跳的最远距离
farthest = Math.max(farthest,i+nums[i]);
//可能碰到0,跳不了了
if(farthest<=i){
return false;
}
}
//当前能到的最远位置大于或等于最后一个索引(n-1),就说明能跳到终点
return farthest >=n-1;
}
}输入:[2,3,1,1,4] 输出:true
思路:
-
站在位置i,最远能跳到 i + nums[i]
-
维护一个全局最远可达 maxReach
-
如果 maxReach >= 最后位置,就能到
过程: i=0: nums[0]=2, maxReach = max(0, 0+2) = 2 i=1: i=1 <= maxReach=2 ✓, nums[1]=3, maxReach = max(2, 1+3) = 4 4 >= 4(最后位置),返回true!
45.跳跃游戏II
题目
给定一个长度为 n 的 0 索引 整数数组 nums。初始位置在下标 0。
每个元素 nums[i] 表示从索引 i 向后跳转的最大长度。换句话说,如果你在索引 i 处,你可以跳转到任意 (i + j) 处:
-
0 <= j <= nums[i]且 -
i + j < n
返回到达 n - 1 的最小跳跃次数。测试用例保证可以到达 n - 1。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。思路
现在的问题是,保证你一定可以跳到最后一格,请问你最少要跳多少次,才能跳过去。
如果使用贪心算法,需要思考贪心选择性质,是否能够通过局部最优解推导全局最优解,避免全量穷举所有的可能解。我们不需要真的递归穷举出所有选择的具体结果来比较求最值,而只需要每次选择那个最有潜力的局部最优解,最终就能得到全局最优解。
比如我可以往前跳2步,跳一步到4,那4能继续跳4步;跳两步到1,1只可以继续跳1步;所以我不是选择当前跳的最远的,而是考虑两步整体跳到最远的。
| 维度 | 55. 跳跃游戏 | 45. 跳跃游戏 II |
|---|---|---|
| 问题 | 能不能跳到最后? | 最少几步跳到最后? |
| 答案类型 | boolean(true/false) |
int(最小步数) |
| 贪心策略 | 维护最远可达距离 | 维护当前步数内最远可达 |
| 遍历方式 | 一次遍历,看能否覆盖终点 | 分层遍历,每步看最远能到哪 |
输入:[2,3,1,1,4] 输出:2
解释:从索引 0 跳 1 步到索引 1,然后再跳 3 步到最后。
思路:
-
每一步(jump)能到达的范围是一个"区间"
-
在这个区间内,找下一步能跳到的最远位置
-
当走到当前区间的尽头,必须再跳一步
过程: 初始:step=0, 当前区间[0,0](只有起点)
step=0的区间[0,0]:
-
i=0, nums[0]=2, 下一步最远到 0+2=2
-
当前区间结束,step++=1, 下一区间[1,2]
step=1的区间[1,2]:
-
i=1, nums[1]=3, 最远到 1+3=4
-
i=2, nums[2]=1, 最远到 2+1=3
-
当前区间结束,step++=2, 下一区间[3,4]
step=2的区间[3,4]:
-
i=3, nums[3]=1, 最远到 4
-
i=4, 到达终点!
-
但已经在终点,不需要再step++
结果:2步
代码
java
class Solution {
public int jump(int[] nums) {
int n = nums.length;
if (n == 1) return 0;
int steps = 0; // 已用步数
int curEnd = 0; //当前步数能到达的最远位置(区间右边界)
int maxReach = 0; //下一步能到达的最远位置
for (int i = 0; i < n - 1; i++) { // 注意:不到最后一个元素
// 在当前步数范围内,找下一步最远能到哪
maxReach = Math.max(maxReach, i + nums[i]);
//到达当前区间的尽头,必须再跳一步
if (i == curEnd) {
steps++;
//更新下一区间的右边界
curEnd = maxReach;
// 提前结束
if (curEnd >= n - 1) break;
}
}
return steps;
}
}1005.K次取反后最大化的数组和
题目
给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组:
选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。重复这个过程恰好 k 次。可以多次选择同一个下标 i 。以这种方式修改数组后,返回数组 可能的最大和 。
示例 1:
输入:nums = [4,2,3], k = 1
输出:5
解释:选择下标 1 ,nums 变为 [4,-2,3] 。示例 2:
输入:nums = [2,-3,-1,5,-4], k = 2
输出:13
解释:选择下标 (1, 4) ,nums 变为 [2,3,-1,5,4] 。思路
如何可以让数组和最大呢?
贪心的思路,局部最优:让绝对值大的负数变为正数,当前数值达到最大,整体最优:整个数组和达到最大。
局部最优可以推出全局最优。
那么如果将负数都转变为正数了,K依然大于0,此时的问题是一个有序正整数序列,如何转变K次正负,让 数组和 达到最大。
那么又是一个贪心:局部最优:只找数值最小的正整数进行反转,当前数值和可以达到最大(例如正整数数组{5, 3, 1},反转1 得到-1 比 反转5得到的-5 大多了),全局最优:整个 数组和 达到最大。
那么本题的解题步骤为:
-
第一步:将数组按照绝对值大小从大到小排序,注意要按照绝对值的大小
-
第二步:从前向后遍历,遇到负数将其变为正数,同时K--
-
第三步:如果K还大于0,那么反复转变数值最小的元素,将K用完
-
第四步:求和
代码
java
class Solution {
public int largestSumAfterKNegations(int[] nums, int k) {
if (nums.length == 1) return nums[0];
// 排序:先把负数处理了
Arrays.sort(nums);
for (int i = 0; i < nums.length && k > 0; i++) { // 贪心点, 通过负转正, 消耗尽可能多的k
if (nums[i] < 0) {
nums[i] = -nums[i];
k--;
}
}
//退出循环, k > 0||k<0(k消耗完了不用讨论)
if (k % 2 == 1) { // k > 0 && k is odd:对于负数:负-正-负-正
Arrays.sort(nums); // 再次排序得到剩余的负数,或者最小的正数
nums[0] = -nums[0];
}
// k > 0 && k is even,flip数字不会产生影响: 对于负数: 负-正-负;对于正数:正-负-正
int sum = 0;
for (int num : nums) { // 计算最大和
sum += num;
}
return sum;
}
}