【算法基础篇】（六十）Nim 博弈超全解析：从基础原理到经典变种，玩转多堆取石子问题

前言

在算法竞赛的博弈论体系中，Nim 博弈是继巴什博弈之后的核心模型，也是公平组合游戏（ICG）中最经典的多堆取石子问题。如果说巴什博弈是入门博弈论的敲门砖，那么 Nim 博弈就是打通博弈论任督二脉的关键 ------ 它跳出了单堆石子的限制，引入了异或运算这一核心工具，其思想更是延伸到阶梯型 Nim、Georgia and Bob 等经典变种问题中。本文将从 Nim 博弈的基础定义出发，深入推导核心结论，结合实战例题讲解代码实现，再剖析其经典变种的解题思路，让你彻底掌握 Nim 博弈的精髓，轻松解决各类多堆取石子问题。下面就让我们正式开始吧！

一、Nim 博弈的前置知识回顾

在正式讲解 Nim 博弈之前，我们先快速回顾博弈论的核心概念，这是理解 Nim 博弈的基础，尤其是公平组合游戏 和必胜态 / 必败态的定义，Nim 博弈作为典型的公平组合游戏，完全遵循这两大核心原则。

1.1 公平组合游戏 (ICG)

满足以下三个条件的游戏即为公平组合游戏：

两名玩家轮流决策，双方完全知晓游戏的所有信息，无任何隐藏规则；

玩家在某一确定状态下的决策集合仅与当前状态有关，与玩家身份无关（双方操作规则完全对等）；

游戏以玩家无法行动为判负条件，且一定会在有限步内结束，不存在平局。

1.2 必胜态与必败态

由于博弈论中默认玩家都是绝顶聪明的（会选择对自己最有利的最优策略），因此游戏的每个状态都有唯一的结果：

必胜态：当前行动的玩家，存在至少一种操作，让对方陷入必败态，最终自己必胜；

必败态：当前行动的玩家，无论采取何种操作，都会让对方进入必胜态，最终自己必败。

而推导必胜态和必败态的核心依据永远是两点：

必胜态的后继状态中，至少存在一个必败态；

必败态的后继状态中，全部都是必胜态。

Nim 博弈的核心结论，正是基于这一依据通过严格的数学推导得出，而非单纯的经验总结。

二、经典 Nim 博弈：多堆取石子的核心原理

2.1 经典 Nim 博弈的问题描述

Nim 博弈的经典场景是多堆石子取物游戏，规则十分简洁：

有n 堆石子 ，每堆石子的数量分别为a1,a2,a3,...,an；两名玩家轮流进行操作，每次可以选择任意一堆石子 ，从中取走任意数量的石子（至少取 1 颗，最多可取完整堆）；取走最后一颗石子的玩家获胜。问：先手玩家是否存在必胜策略？

与巴什博弈的单堆石子不同，Nim 博弈的核心是多堆石子的组合状态 ，其胜负判断不再依赖简单的取模运算，而是引入了位运算中的异或操作，这也是 Nim 博弈最精妙的地方。

2.2 Nim 博弈的核心结论

先直接给出 Nim 博弈的终极结论，这是解决所有 Nim 博弈问题的核心，必须牢记：

对于 n 堆石子的 Nim 博弈，设每堆石子数为a1,a2,...,an，计算所有石子数的异或和 ：s=a1⊕a2⊕a3⊕...⊕an

若异或和 s ≠ 0 ，则先手必胜；

若异或和 s = 0 ，则先手必败。

其中⊕表示位运算中的异或操作 （C++ 中用^符号表示），异或运算的核心规则是：相同为 0，不同为 1（如 1⊕1=0，1⊕0=1，0⊕0=0）。

举个简单的例子：

3 堆石子数为 [3,6,9]，异或和为 3^6^9 = 0 → 先手必败；

4 堆石子数为 [7,12,9,15]，异或和为 7^12^9^15 ≠ 0 → 先手必胜。

这两个例子正是后续实战例题的原型，我们会在代码实现中验证结果。

2.3 核心结论的严格数学证明

Nim 博弈的结论看似简单，但背后的数学证明至关重要，理解证明过程能让你真正掌握 Nim 博弈的思想，而非死记硬背结论。证明的核心思路依旧围绕必胜态和必败态的两大核心依据，分两步证明：

证明前提：定义基准必败态

当所有堆的石子数都为 0 时（a1=a2=...=an=0），当前玩家无石子可取，处于必败态，此时异或和s=0，与结论一致。

第一步：证明「异或和 s≠0」是必胜态

即：当异或和s≠0时，当前玩家（先手）一定存在一种操作，使得操作后的异或和变为 0，将必败态交给后手。

详细推导：

设异或和s=a1⊕a2⊕...⊕an≠0，观察 s 的二进制表示，找到其最高位的 1，设该位为第 k 位；

由于 s 的第 k 位为 1，说明在a1,a2,...,an中，必定有奇数个堆的石子数的第 k 位为 1（异或运算的规则：相同位 1 的个数为奇数时，结果为 1）；

任选其中一个第 k 位为 1 的堆，设其石子数为ai，计算ai′=ai⊕s；

由于 s 的最高位是 k，且ai的第 k 位为 1，因此ai′=ai⊕s<ai（第 k 位由 1 变 0，高位变小，整体数值一定减小）；

将第 i 堆的石子数从ai变为ai′（即取走ai−ai′颗石子），此时新的异或和为：a1⊕a2⊕...⊕ai′⊕...⊕an=a1⊕a2⊕...⊕(ai⊕s)⊕...⊕an=(a1⊕a2⊕...⊕an)⊕s=s⊕s=0

由此可知，当 s≠0 时，先手总能找到这样一堆石子，通过取走部分石子让异或和变为 0，将必败态交给后手，因此s≠0 是必胜态。

第二步：证明「异或和 s=0」是必败态

即：当异或和 s=0 时，当前玩家（先手）无论采取何种操作，操作后的异或和一定不为 0，让后手进入必胜态。

详细推导：

设异或和s=a1⊕a2⊕...⊕an=0，当前玩家选择某一堆ai，取走部分石子后使其变为ai′，其中0≤ai′<ai；

假设操作后的异或和仍为 0，即：a1⊕a2⊕...⊕ai′⊕...⊕an=0

将上述两个式子进行异或操作，可得：(a1⊕...⊕ai⊕...⊕an)⊕(a1⊕...⊕ai′⊕...⊕an)=0⊕0=0

根据异或运算的结合律和交换律，相同项异或为 0，最终可得：ai⊕ai′=0，即ai=ai′；

这与ai′<ai的前提矛盾，因此假设不成立，操作后的异或和一定不为 0。

由此可知，当 s=0 时，先手无论怎么操作，都会让异或和变为非 0，后手进入必胜态，因此s=0 是必败态。

至此，Nim 博弈的核心结论通过严格的数学证明得以验证，异或运算成为判断多堆取石子问题胜负的核心工具，这一思想也将贯穿所有 Nim 博弈的变种问题。

三、经典 Nim 博弈的实战例题与代码实现

理论结合实践是掌握算法的关键，本节将结合两道经典的 Nim 博弈例题，从基础模板题到带操作方案的进阶题，逐一讲解解题思路，并附上完整的 C++ 代码实现，所有代码均可直接用于算法竞赛。

3.1 例题 1：取石子游戏 2（Nim 博弈基础模板题）

题目链接：https://ac.nowcoder.com/acm/problem/50615

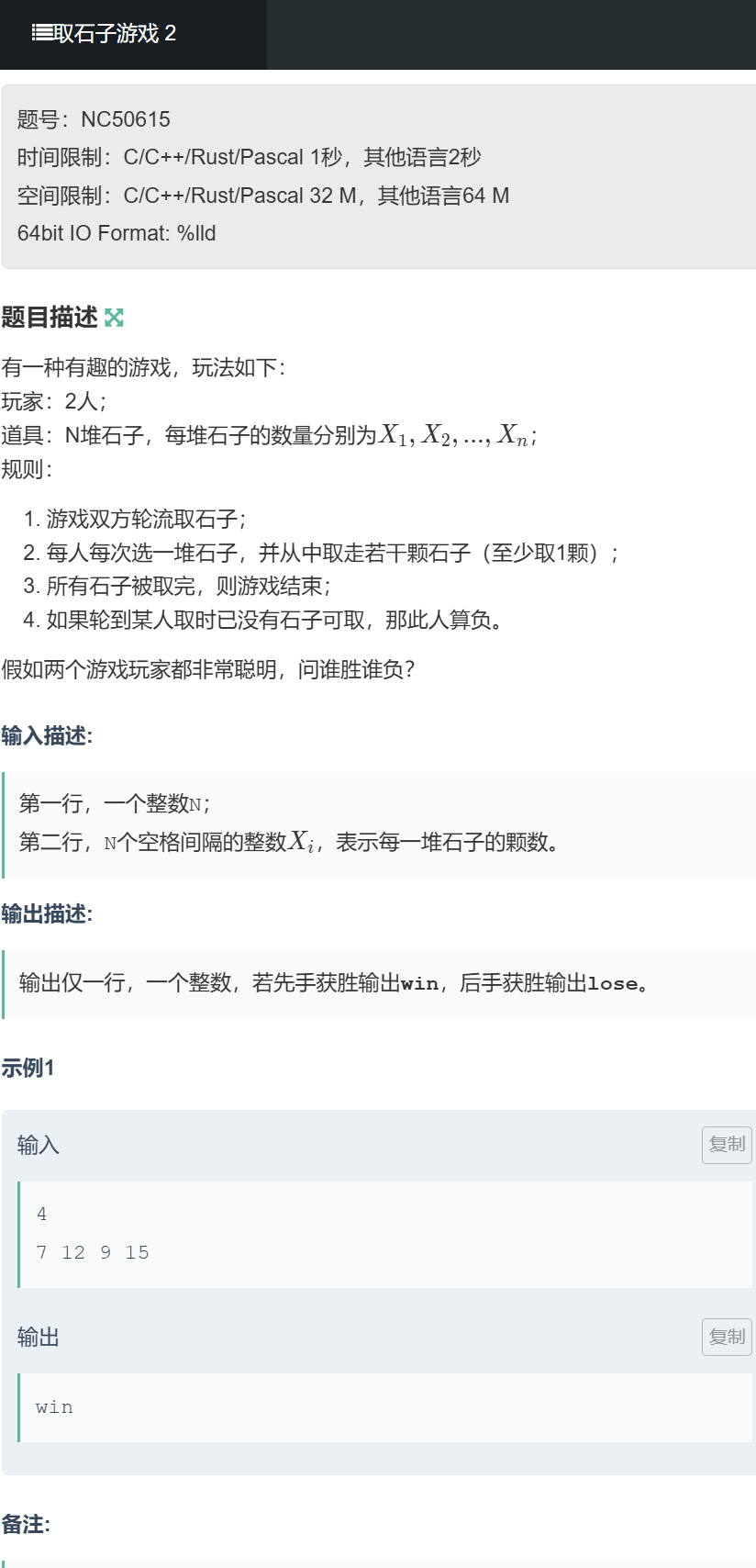
题目来源

牛客网（信息学奥赛一本通）

题目描述

玩家为 2 人，道具为 N 堆石子，每堆石子数为X1,X2,...,XN，规则如下：

双方轮流取石子，每次选择任意一堆，取走至少 1 颗石子；
所有石子取完游戏结束，无法取石子的一方判负；
玩家均绝顶聪明，问先手是否必胜？

输入描述

第一行：一个整数 N，表示石子的堆数；
第二行：N 个空格分隔的整数Xi，表示每堆石子的数量。

输出描述

输出仅一行，若先手必胜输出win，后手必胜输出lose。

解题思路

这是最标准的 Nim 博弈模板题，直接套用核心结论即可：

初始化异或和为 0；

遍历每堆石子数，依次进行异或运算；

最终若异或和≠0，输出win；否则输出lose。

C++ 代码实现

cpp 复制代码

#include <iostream>
using namespace std;

int main() {
    int n;
    cin >> n;
    int ret = 0; // 初始化异或和为0
    for (int i = 0; i < n; i++) {
        int x;
        cin >> x;
        ret ^= x; // 依次异或每堆石子数
    }
    if (ret) { // 异或和不为0，先手必胜
        cout << "win" << endl;
    } else { // 异或和为0，先手必败
        cout << "lose" << endl;
    }
    return 0;
}

示例测试

输入：47 12 9 15

计算：7^12=11，11^9=2，2^15=13 ≠ 0 → 先手必胜

输出：win与题目示例一致，验证代码正确性。

3.2 例题 2：取火柴游戏（Nim 博弈进阶：输出操作方案）

题目链接：https://www.luogu.com.cn/problem/P1247

题目来源

洛谷 P1247

题目描述

输入 k 及 k 个整数n1,n2,...,nk，表示 k 堆火柴棒，每堆根数为ni；两名玩家轮流取火柴，规则与经典 Nim 博弈一致，取走最后一根火柴的玩家获胜。

要求：判断先手是否必胜，若必胜则输出第一次的操作方案 （字典序最小），若必败则输出lose。

**操作方案：**两个整数 a、b，表示从第 b 堆取出 a 根火柴；

**字典序最小：**优先选择堆数 b 最小的，若有多个则选择取出数量 a 最小的。

输入描述

第一行：正整数 k，表示火柴堆数；
第二行：k 个整数，表示每堆火柴的根数。

输出描述

若必败：输出lose；
若必胜：第一行输出 a、b，第二行输出取火柴后的状态。

解题思路

本题是 Nim 博弈的进阶题，不仅要判断胜负，还要输出字典序最小的操作方案，解题思路分为两步：

判断胜负 ：计算所有堆的异或和 ret，若 ret=0 则必败，输出lose；

寻找操作方案：遍历每一堆（从左到右，保证字典序最小），对于第 i 堆的石子数a[i]，计算t=a[i]⊕ret，若t<a[i]，则从第 i 堆取出a[i]−t颗石子（此时第 i 堆变为 t，整体异或和变为 0），这就是字典序最小的方案。

关键原理

根据 Nim 博弈的证明，当异或和为 ret≠0 时，找到第一个满足a[i]⊕ret<a[i]的堆 i，就是字典序最小的堆，取出的数量为a[i]−(a[i]⊕ret)。

C++ 代码实现

cpp 复制代码

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 5e5 + 10; // 数据范围适配算法竞赛
int a[N]; // 存储每堆石子/火柴的数量

int main() {
    int n;
    cin >> n;
    int ret = 0;
    for (int i = 1; i <= n; i++) { // 堆数从1开始，符合题目输出习惯
        cin >> a[i];
        ret ^= a[i];
    }
    if (ret == 0) { // 异或和为0，先手必败
        cout << "lose" << endl;
    } else { // 寻找字典序最小的操作方案
        for (int i = 1; i <= n; i++) {
            int t = a[i] ^ ret;
            if (t < a[i]) { // 找到符合条件的堆
                int take = a[i] - t; // 取出的数量
                cout << take << " " << i << endl;
                a[i] = t; // 更新该堆的数量
                break;
            }
        }
        // 输出操作后的状态
        for (int i = 1; i <= n; i++) {
            cout << a[i] << " ";
        }
        cout << endl;
    }
    return 0;
}

示例测试

输入：33 6 9

计算：3^6^9 = 0 → 先手必败

输出：lose

四、Nim 博弈的经典变种：阶梯型 Nim 博弈

掌握经典 Nim 博弈后，其各类变种问题都是在经典模型的基础上做规则变形 ，核心思路依旧是将变种问题转化为经典 Nim 博弈 ，其中阶梯型 Nim 博弈是最经典、最常考的变种，也是算法竞赛中的高频考点。

4.1 阶梯型 Nim 博弈的问题描述

有1~n 级台阶 ，第 i 级台阶上放有a[i]个石子；两名玩家轮流进行操作，每次可以选择任意一级台阶 ，将其中任意数量的石子（至少 1 颗）移动到下一级台阶 ；石子移到地面（0 级台阶）后无法再移动，移走最后一颗石子的玩家获胜。问：先手是否存在必胜策略？

4.2 阶梯型 Nim 博弈的核心结论

阶梯型 Nim 博弈的核心是忽略偶数级台阶，只考虑奇数级台阶的经典 Nim 博弈，结论十分简洁：

计算所有奇数级台阶 的石子数的异或和：s=a[1]⊕a[3]⊕a[5]⊕...

若s ≠ 0 ，则先手必胜；

若s = 0 ，则先手必败。

简单来说，阶梯型 Nim 博弈的胜负，仅由奇数级台阶的石子分布决定，偶数级台阶只是 "中转站"，不影响最终结果。

4.3 结论的通俗证明

为什么阶梯型 Nim 博弈只需要考虑奇数级台阶？我们可以通过必胜态 / 必败态的核心逻辑 和模仿操作策略来通俗证明，无需复杂的数学推导：

当后手移动偶数级台阶的石子 ：若后手将第 k 级（偶数）的石子移到 k-1 级（奇数），先手可以直接将这部分石子从 k-1 级移到 k-2 级（偶数），最终让这部分石子回到偶数级台阶，相当于后手的操作被抵消，奇数级台阶的石子分布不变；

当后手移动奇数级台阶的石子 ：若后手将第 k 级（奇数）的石子移到 k-1 级（偶数），这相当于经典 Nim 博弈中取走了第 k 级的部分石子，此时先手可以按照经典 Nim 博弈的策略，对其他奇数级台阶进行操作，让奇数级台阶的异或和回到 0；

最终结果 ：所有石子最终都会从奇数级台阶移到偶数级，再移到地面，因此谁能掌控奇数级台阶的石子，谁就能获胜，而偶数级台阶只是过渡，无法影响胜负。

由此可知，阶梯型 Nim 博弈的本质，就是奇数级台阶的经典 Nim 博弈。

4.4 阶梯型 Nim 博弈的代码实现

阶梯型 Nim 博弈的代码实现十分简单，只需在经典 Nim 博弈的基础上，仅遍历奇数级台阶进行异或运算即可：

cpp 复制代码

#include <iostream>
using namespace std;

int main() {
    int n;
    cin >> n;
    int ret = 0;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        if (i & 1) { // 仅对奇数级台阶进行异或（i&1为1表示奇数）
            ret ^= x;
        }
    }
    if (ret) {
        cout << "win" << endl; // 先手必胜
    } else {
        cout << "lose" << endl; // 先手必败
    }
    return 0;
}

五、阶梯型 Nim 博弈的实战变种例题

阶梯型 Nim 博弈的核心思想可以延伸到各类移动型取物游戏 中，比如格子移石子、棋盘移棋子等，这类问题的解题关键是将问题转化为阶梯型 Nim 博弈，找到对应的 "奇数级台阶"。本节将结合两道经典例题，讲解阶梯型 Nim 博弈的实际应用。

5.1 例题 1：lyw 的石子游戏（格子移石子）

题目链接：https://ac.nowcoder.com/acm/problem/218562

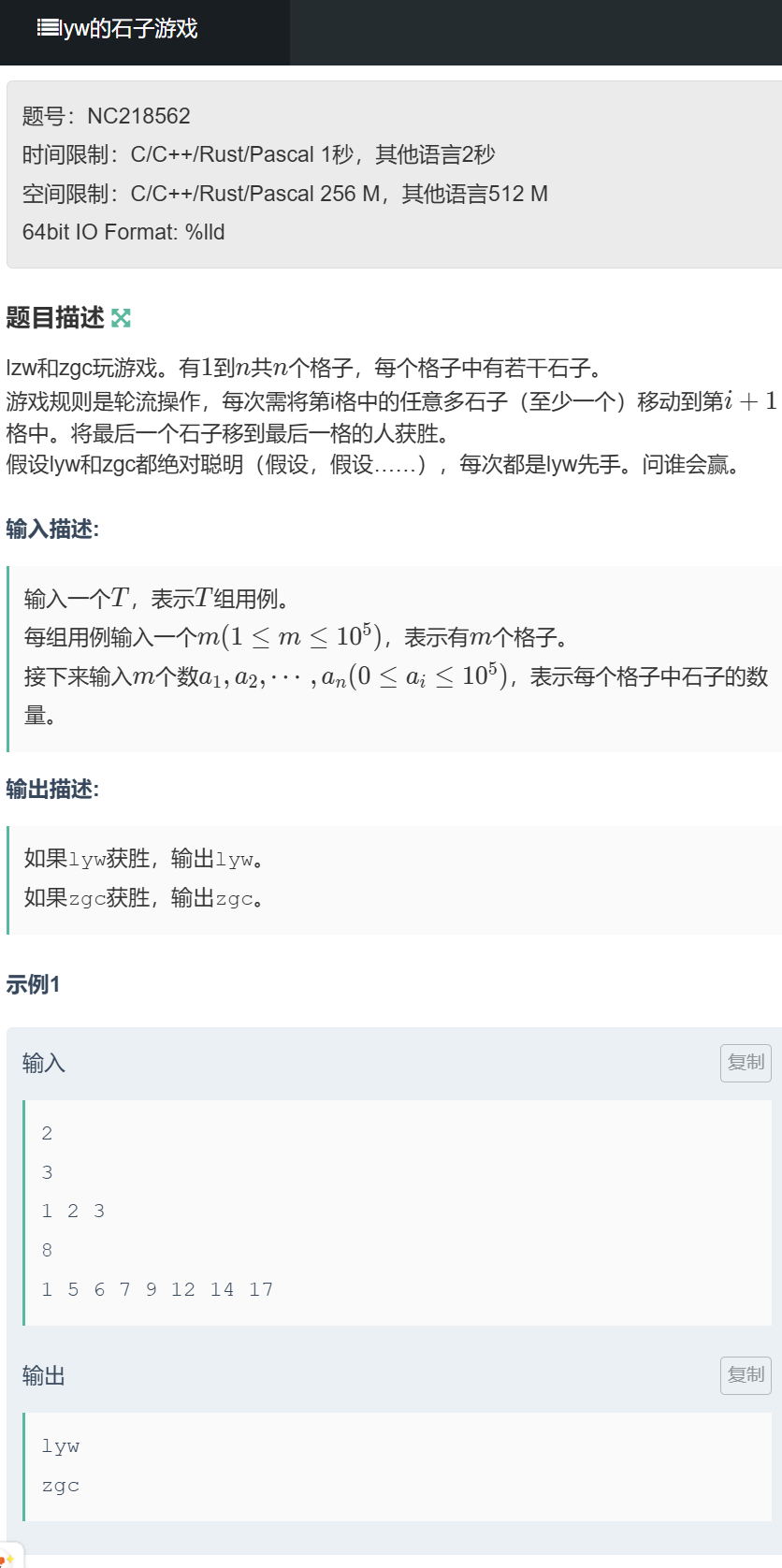
题目来源

牛客网

题目描述

有 1~n 个格子，每个格子中有若干石子；两名玩家轮流操作，每次将第 i 格中的任意数量石子（至少 1 颗）移动到第 i+1 格 ；将最后一颗石子移到最后一格的玩家获胜。lyw 为先手，问谁会赢？

解题思路

本题是阶梯型 Nim 博弈的经典变形 ，解题的关键是重新定义 "台阶"：

最后一格是终点，石子移到最后一格后无法再移动，因此第 n 格相当于地面；

能影响胜负的是第 n-1、n-3、n-5... 格（即从后往前的奇数位），相当于阶梯型 Nim 的奇数级台阶；

因此，只需计算从 n-1 开始的奇数位格子的石子数异或和，若异或和≠0 则先手（lyw）必胜，否则后手必胜。

C++ 代码实现

cpp 复制代码

#include <iostream>
using namespace std;

const int N = 1e5 + 10;
int a[N];

int main() {
    int T;
    cin >> T; // 多组测试用例
    while (T--) {
        int n;
        cin >> n;
        for (int i = 1; i <= n; i++) {
            cin >> a[i];
        }
        int ret = 0;
        // 从n-1开始，步长为-2，遍历奇数位
        for (int i = n - 1; i >= 1; i -= 2) {
            ret ^= a[i];
        }
        if (ret) {
            cout << "lyw" << endl; // 先手必胜
        } else {
            cout << "zgc" << endl; // 后手必胜
        }
    }
    return 0;
}

5.2 例题 2：Georgia and Bob（棋盘移棋子）

题目链接：https://www.luogu.com.cn/problem/P10507

题目来源

洛谷 P10507

题目描述

有一个无限长的棋盘，从左到右编号为 1,2,3,...；棋盘上有 n 个棋子，位置互不相同；两名玩家轮流操作，每次将一枚棋子向左移动至少 1 格 ，不能逾越其他棋子，不能与其他棋子重合，不能移出棋盘 ；无法操作的玩家判负，Georgia 为先手，问谁会赢？

解题思路

本题是阶梯型 Nim 博弈的经典进阶变形 ，看似是移棋子，实则可以转化为台阶移石子，解题分为三步：

排序棋子位置：将棋子的位置按从小到大排序，设为p[1],p[2],...,p[n]；

计算相邻棋子的空格数 ：定义a[i]=p[i]−p[i−1]−1（p [0]=0），表示第 i 颗棋子向左可移动的最大空格数；

阶梯型 Nim 博弈 ：仅考虑偶数位的 a [i]（或从后往前的奇数位），计算其异或和，若异或和≠0 则先手必胜，否则后手必胜。

核心转化

棋子的向左移动，等价于阶梯型 Nim 中石子的向下移动，相邻棋子的空格数就是台阶上的石子数，而偶数位的空格数就是决定胜负的 "奇数级台阶"。

C++ 代码实现

cpp 复制代码

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;
int p[N], a[N];

int main() {
    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        for (int i = 1; i <= n; i++) {
            cin >> p[i];
        }
        sort(p + 1, p + 1 + n); // 排序棋子位置
        int ret = 0;
        for (int i = 1; i <= n; i++) {
            a[i] = p[i] - p[i-1] - 1; // 计算空格数
        }
        // 从后往前遍历奇数位的空格数
        for (int i = n; i >= 1; i -= 2) {
            ret ^= a[i];
        }
        if (ret) {
            cout << "Georgia will win" << endl;
        } else {
            cout << "Bob will win" << endl;
        }
    }
    return 0;
}

总结

Nim 博弈的精髓不在于死记硬背异或和的结论，而在于理解其背后的必胜态 / 必败态推导逻辑 ，以及将变种问题转化为经典模型的思维能力 。从单堆的巴什博弈到多堆的 Nim 博弈，再到移动型的阶梯型 Nim 博弈，博弈论的学习始终围绕 "找规律、做转化" 两大核心，而这也是算法竞赛的核心能力。

希望本文能帮助你彻底掌握 Nim 博弈的基础原理和经典变种，在后续的博弈论学习中打下坚实的基础。后续我会继续讲解 SG 函数、威佐夫博弈等进阶模型，关注我，一起玩转算法竞赛的博弈论！

【算法基础篇】（六十）Nim 博弈超全解析：从基础原理到经典变种，玩转多堆取石子问题

目录

前言

一、Nim 博弈的前置知识回顾

1.1 公平组合游戏 (ICG)

1.2 必胜态与必败态

二、经典 Nim 博弈：多堆取石子的核心原理

2.1 经典 Nim 博弈的问题描述

2.2 Nim 博弈的核心结论

2.3 核心结论的严格数学证明

证明前提：定义基准必败态

第一步：证明「异或和 s≠0」是必胜态

第二步：证明「异或和 s=0」是必败态

三、经典 Nim 博弈的实战例题与代码实现

3.1 例题 1：取石子游戏 2（Nim 博弈基础模板题）

题目来源

题目描述

输入描述

输出描述

解题思路

C++ 代码实现

示例测试

3.2 例题 2：取火柴游戏（Nim 博弈进阶：输出操作方案）

题目来源

题目描述

输入描述

输出描述

解题思路

关键原理

C++ 代码实现

示例测试

四、Nim 博弈的经典变种：阶梯型 Nim 博弈

4.1 阶梯型 Nim 博弈的问题描述

4.2 阶梯型 Nim 博弈的核心结论

4.3 结论的通俗证明

4.4 阶梯型 Nim 博弈的代码实现

五、阶梯型 Nim 博弈的实战变种例题

5.1 例题 1：lyw 的石子游戏（格子移石子）

题目来源

题目描述

解题思路

C++ 代码实现

5.2 例题 2：Georgia and Bob（棋盘移棋子）

题目来源

题目描述

解题思路

核心转化

C++ 代码实现

总结