数据结构初阶：排序算法全解析（下）

目录

• 前言
• 二、常见排序算法详解（含完整代码+核心注释）
• [2.3 交换排序](#2.3 交换排序)
• [2.3.1 冒泡排序](#2.3.1 冒泡排序)
• [2.3.2 快速排序](#2.3.2 快速排序)
• [2.4 归并排序](#2.4 归并排序)
• [2.5 非比较排序------计数排序](#2.5 非比较排序——计数排序)
• 三、排序算法性能对比（基于10万条随机数据测试，参考值）
• 四、排序算法复杂度及稳定性总览
• 总结

---

前言

跳转上篇：数据结构初阶：排序算法全解析（上）

本文主要学习上篇没有学习完的排序算法（快速排序，归并排序，计数排序），以及对所有排序算法的性能的汇总比较。没有绝对好坏的排序算法，每个算法都有优缺点，需要根据具体情况具体分析。

---

二、常见排序算法详解（含完整代码+核心注释）

2.3 交换排序

2.3.1 冒泡排序

跳转上篇：数据结构初阶：排序算法全解析（上）

2.3.2 快速排序

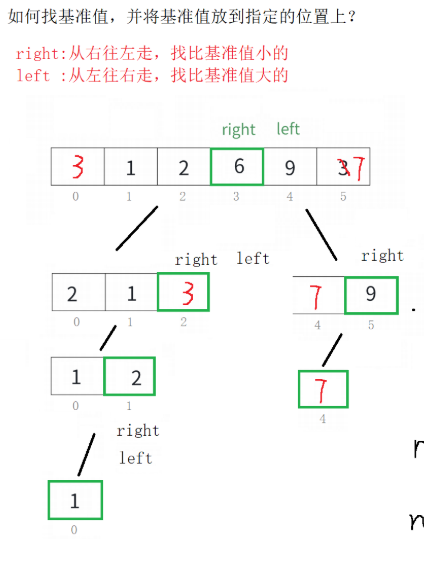
• 基本思想：选基准值，将数组划分为"左小右大"两部分（左区间元素均≤基准值，右区间元素均≥基准值），递归处理左右子区间，是实际应用中效率极高的排序算法（平均效率最优）。

• 常见划分方法

  • Hoare版本 ：左右指针相向扫描，右指针先找比基准小的元素，左指针再找比基准大的元素，交换后继续，最终基准值归位（跳出循环后right 位置元素必不大于基准值）。

  • 挖坑法：先存基准值形成"坑"，右指针找小元素填左坑，左指针找大元素填右坑，循环后基准值填最终坑位，划分逻辑更直观。（选择学习）

  • 前后指针法 ：prev 指向已排序区间末尾，cur 扫描找小于基准值的元素，++prev 后交换，扩展有序区间，效率较高，不易出错。

• 非递归实现：借助栈模拟递归过程，存储待排序区间的左右边界，避免递归栈溢出（适用于大规模数据，防止递归深度过大导致崩溃）。（代码未展现）

• 代码实现

#include <stdio.h>
#include <stdlib.h>

// 交换函数（复用）
void swap(int* a, int* b) {
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

// 1. Hoare版本划分（左右指针法）
int _QuickSortHoare(int* a, int left, int right) {
    int keyi = left; // 选择左端点为基准值（可优化为三数取中，避免最坏情况）
    int begin = left, end = right;
    while (left < right) {
        // 右指针先找比基准小的元素（防止基准值归位后位置错误）
        while (left < right && a[right] >= a[keyi]) right--;
        // 左指针找比基准大的元素
        while (left < right && a[left] <= a[keyi]) left++;
        swap(&a[left], &a[right]); // 交换逆序元素
    }
    swap(&a[keyi], &a[right]); // 基准值归位（left == right）
    return right; // 返回基准值最终位置
}

// 2. 挖坑法划分
int _QuickSortHole(int* a, int left, int right) {
    int key = a[left]; // 保存基准值，形成第一个坑（left位置）
    int hole = left;
    while (left < right) {
        // 右指针找小元素，填左坑
        while (left < right && a[right] >= key) right--;
        a[hole] = a[right];
        hole = right; // 新坑位置更新为right
        // 左指针找大元素，填右坑
        while (left < right && a[left] <= key) left++;
        a[hole] = a[left];
        hole = left; // 新坑位置更新为left
    }
    a[hole] = key; // 基准值填入最终坑位，完成划分
    return hole; // 返回基准值位置
}

// 3. 前后指针法划分（推荐，效率高）
int _QuickSortPrevCur(int* a, int left, int right) {
    int keyi = left; // 基准值索引
    int prev = left, cur = left + 1; // prev指向已排序区间末尾，cur扫描整个区间
    while (cur <= right) {
        // 找到小于基准值的元素，交换到已排序区间末尾
        if (a[cur] < a[keyi] && ++prev != cur) {
            swap(&a[prev], &a[cur]);
        }
        cur++; // cur继续扫描下一个元素
    }
    swap(&a[keyi], &a[prev]); // 基准值归位（与prev位置元素交换）
    return prev; // 返回基准值位置
}

// 快速排序递归主框架（可替换三种划分方法）
void QuickSort(int* a, int left, int right) {
    if (left >= right) return; // 区间长度为1或0，无需排序
    // 此处可替换为_QuickSortHoare、_QuickSortHole
    int meet = _QuickSortPrevCur(a, left, right); 
    QuickSort(a, left, meet - 1); // 递归处理左子区间
    QuickSort(a, meet + 1, right); // 递归处理右子区间
}

• 特性总结

  • 平均效率最优，适合大规模数据排序，实际开发中应用最广泛（如C++ STL的sort函数底层优化版本）。

  • 时间复杂度：O(NlogN)（最好、平均）；O(N^2)（最坏，数据有序或逆序，可通过"三数取中"选择基准值优化）。

  • 空间复杂度：O(logN)（递归栈，平均情况）；O(N)（最坏情况），不稳定排序。

  • 补充：优化技巧------三数取中（选择左、中、右三个位置的中间值作为基准值）、插入排序优化（子区间长度较小时，用直接插入排序替代递归，提升效率）。

2.4 归并排序

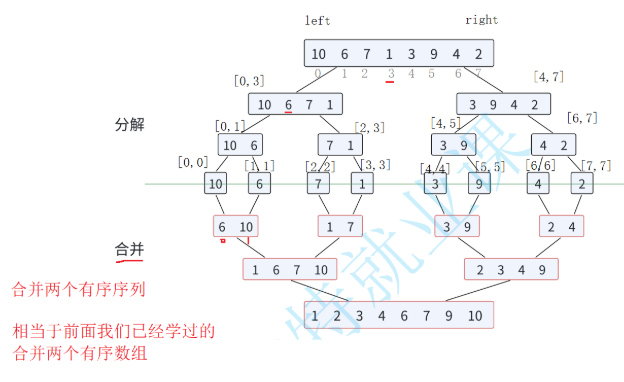
• 基本思想 ：分治法的典型应用，核心是"分而治之"------先将数组递归拆分为[left, mid] 和 [mid+1, right] 两个子区间，子区间排序后再合并为有序数组，合并过程是核心。

• 核心步骤

  • 分解：递归拆分数组，直到子区间长度为1（长度为1的子数组天然有序）。

  • 合并：用临时数组合并两个有序子区间，将两个子区间的元素按顺序比较，依次存入临时数组，最后将临时数组的元素拷贝回原数组，确保合并后数组有序。

• 代码实现

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// 合并两个有序子区间[left, mid]和[mid+1, right]
void _Merge(int* a, int left, int mid, int right, int* tmp) {
    int begin1 = left, end1 = mid; // 第一个有序子区间的边界
    int begin2 = mid + 1, end2 = right; // 第二个有序子区间的边界
    int index = left; // 临时数组的索引（与原数组left对齐，方便后续拷贝）
    
    // 比较两个子区间的元素，依次存入临时数组
    while (begin1 <= end1 && begin2 <= end2) {
        tmp[index++] = a[begin1] < a[begin2] ? a[begin1++] : a[begin2++];
    }
    // 拷贝第一个子区间的剩余元素
    while (begin1 <= end1) tmp[index++] = a[begin1++];
    // 拷贝第二个子区间的剩余元素
    while (begin2 <= end2) tmp[index++] = a[begin2++];
    // 将临时数组中排序好的元素，拷贝回原数组对应位置
    memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));
}

// 归并排序递归核心（拆分+合并）
void _MergeSort(int* a, int left, int right, int* tmp) {
    if (left >= right) return; // 子区间长度为1或0，无需排序
    int mid = (left + right) / 2; // 拆分点（中间位置）
    // 递归拆分左子区间[left, mid]
    _MergeSort(a, left, mid, tmp);
    // 递归拆分右子区间[mid+1, right]
    _MergeSort(a, mid + 1, right, tmp);
    // 合并两个有序子区间
    _Merge(a, left, mid, right, tmp);
}

// 归并排序入口函数（申请临时数组，避免递归中重复申请）
void MergeSort(int* a, int n) {
    // 申请临时数组（用于合并操作，大小与原数组一致）
    int* tmp = (int*)malloc(sizeof(int) * n);
    if (tmp == NULL) {
        perror("malloc fail");
        return;
    }
    // 调用递归核心函数
    _MergeSort(a, 0, n - 1, tmp);
    // 释放临时数组，避免内存泄漏
    free(tmp);
    tmp = NULL;
}

• 特性总结

  • 稳定的高效排序算法，是唯一一种稳定且时间复杂度为O(NlogN)的排序算法，适合对稳定性有要求的场景。

  • 时间复杂度：O(NlogN)（最好、最坏、平均），效率稳定，与数据有序性无关。

  • 空间复杂度：O(N)（临时数组，用于合并操作），非原地排序。

  • 补充：适合大规模数据、对稳定性有要求的场景（如多关键字排序），缺点是需要额外的临时空间，内存消耗略大。

2.5 非比较排序------计数排序

• 基本思想：利用"鸽巢原理"，通过数组下标统计元素出现次数，无需元素间两两比较，适用于数据范围集中的整数排序场景，效率极高。

• 核心步骤

  • 找出数组的最大值 max 和最小值 min，确定统计范围 range = max - min + 1（减少空间浪费，避免因最小值过大导致统计数组冗余）。

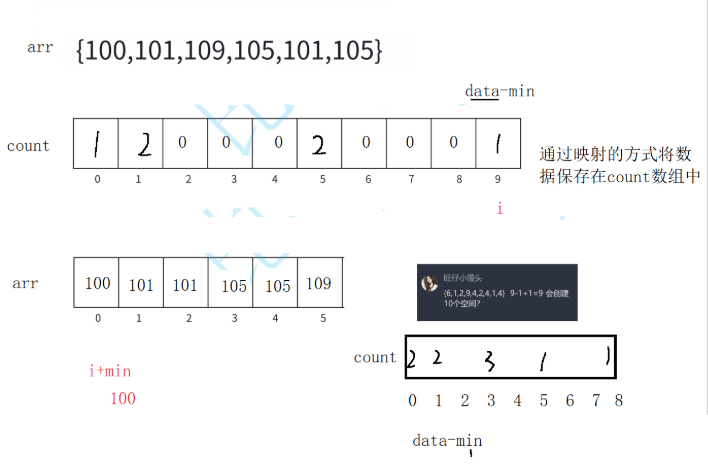
  • 用 count 数组统计每个元素（映射为 a[i]-min 下标）的出现次数（下标对应元素值，数组值对应出现次数）。

  • 根据 count 数组，将元素按顺序回填到原数组（遍历count数组，根据出现次数依次填入对应元素）。

• 代码实现

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

void CountSort(int* a, int n) {
    if (n <= 1) return; // 数组长度≤1，无需排序
    int min = a[0], max = a[0];
    // 1. 找出数组的最大值和最小值，确定统计范围
    for (int i = 1; i < n; i++) {
        if (a[i] > max) max = a[i];
        if (a[i] < min) min = a[i];
    }
    int range = max - min + 1; // 统计范围（避免空间浪费）
    // 2. 申请统计数组并初始化（初始值为0）
    int* count = (int*)malloc(sizeof(int) * range);
    if (count == NULL) {
        perror("malloc fail");
        return;
    }
    memset(count, 0, sizeof(int) * range); // 初始化count数组为0
    // 3. 统计每个元素的出现次数（元素映射为a[i]-min，对应count数组下标）
    for (int i = 0; i < n; i++) {
        count[a[i] - min]++;
    }
    // 4. 根据count数组，将元素回填到原数组，完成排序
    int j = 0;
    for (int i = 0; i < range; i++) {
        // 出现count[i]次，就填入count[i]个对应元素（i+min）
        while (count[i]--) {
            a[j++] = i + min;
        }
    }
    // 释放统计数组，避免内存泄漏
    free(count);
    count = NULL;
}

• 特性总结

  • 数据范围 range 较小时效率极高（时间复杂度接近$$O(N)$$），无需元素比较，排序速度快。

  • 适用场景有限：仅支持整数排序（无法排序浮点数、字符串等），且 range 不宜过大（否则空间浪费严重）。

  • 时间复杂度：O(N + range)，空间复杂度：O(range)，稳定排序。

  • 补充：适合数据范围小、且为整数的场景（如学生成绩排序、年龄排序），实际开发中可作为高效排序的补充。

三、排序算法性能对比（基于10万条随机数据测试，参考值）

|--------|-----------|------------------------|-------------------------|
| 排序方法 | 运行时间（参考值） | 核心优势 | 适用场景 |
| 直接插入排序 | 700+ms | 数据接近有序时效率高、实现简单、稳定 | 小规模有序/接近有序数据、数据预处理 |
| 希尔排序 | 7-10ms | 对直接插入排序优化，兼顾效率与空间、原地排序 | 中等规模数据，对稳定性无要求 |
| 直接选择排序 | 2600+ms | 思路简单、交换次数少、原地排序 | 学习理解，实际极少使用 |
| 堆排序 | 4-5ms | 空间复杂度低（O(1)）、效率稳定、原地排序 | 大规模数据，内存受限场景，对稳定性无要求 |
| 快速排序 | 0-1ms | 平均效率最优、实际应用广泛、原地排序 | 大规模无序数据，优先选择，对稳定性无要求 |
| 归并排序 | 0-1ms | 稳定排序、效率稳定、适用范围广 | 大规模数据，对稳定性有要求（如多关键字排序） |
| 冒泡排序 | 8800+ms | 实现最简单、易于理解、稳定、原地排序 | 学习入门，实际几乎不使用 |
| 计数排序 | 接近0ms | 数据范围集中时效率极高、稳定 | 整数类型、数据范围小的场景（如成绩、年龄排序） |

四、排序算法复杂度及稳定性总览

|--------|---------------------------|-------------|----------|------|-----|
| 排序方法 | 平均情况 | 最好情况 | 最坏情况 | 辅助空间 | 稳定性 |
| 冒泡排序 | O(N^2) | O(N) | O(N^2) | O(1) | 稳定 |
| 直接选择排序 | O(N^2) | O(N^2) | O(N^2) | O(1) | 不稳定 |
| 直接插入排序 | O(N^2) | O(N) | O(N^2) | O(1) | 稳定 |
| 希尔排序 | O(n^{1.3}) \sim O(N^2) | O(n^{1.3}) | O(N^2) | O(1) | 不稳定 |
| 堆排序 | O(NlogN) | O(NlogN) | O(NlogN) | O(1) | 不稳定 |
| 归并排序 | O(NlogN) | O(NlogN) | O(NlogN) | | |

---

总结

这两篇排序算法笔记围绕排序的基础概念、常见算法详解、性能对比及核心参数展开，先明确排序是按关键字排列记录的基础操作，分比较排序（插入、选择、交换、归并类）与非比较排序（计数排序）两类；再详解每种算法的思想、步骤、可运行代码及特性，如直接插入排序适合小规模有序数据、快速排序平均效率最优、归并排序是稳定的高效算法、计数排序仅适用于小范围整数；最后通过性能测试数据和复杂度/稳定性表，清晰呈现各算法的效率、优势与适用场景。