《机器学习导论》第15章- 隐马尔可夫模型（HMM）

啊阿狸不会拉杆2026-02-12 11:00

目录

前言

[15.1 引言](#15.1 引言)

[15.2 离散马尔科夫过程](#15.2 离散马尔科夫过程)

通俗比喻

[代码实战：离散马尔可夫链模拟 + 可视化](#代码实战：离散马尔可夫链模拟 + 可视化)

运行效果

[15.3 隐马尔科夫模型](#15.3 隐马尔科夫模型)

[核心组成（4 要素）](#核心组成（4 要素）)

通俗比喻

[Mermaid 流程图：HMM 结构](#Mermaid 流程图：HMM 结构)

[代码实战：定义 HMM 模型并可视化结构](#代码实战：定义 HMM 模型并可视化结构)

[15.4 HMM 的三个基本问题](#15.4 HMM 的三个基本问题)

[Mermaid 思维导图：HMM 三个基本问题](#Mermaid 思维导图：HMM 三个基本问题)

[15.5 估值问题](#15.5 估值问题)

核心思想

[代码实战：前向算法实现 + 效果对比](#代码实战：前向算法实现 + 效果对比)

关键结论

[15.6 寻找状态序列（解码问题）](#15.6 寻找状态序列（解码问题）)

核心思想

[代码实战：Viterbi 算法实现 + 可视化](#代码实战：Viterbi 算法实现 + 可视化)

运行效果

[15.7 学习模型参数（Baum-Welch 算法）](#15.7 学习模型参数（Baum-Welch 算法）)

核心思想

[代码实战：Baum-Welch 算法实现](#代码实战：Baum-Welch 算法实现)

关键结论

[15.8 连续观测](#15.8 连续观测)

核心思想

[代码实战：连续观测 HMM 实现](#代码实战：连续观测 HMM 实现)

[15.9 HMM 作为图模型](#15.9 HMM 作为图模型)

[Mermaid 图：HMM 概率图模型](#Mermaid 图：HMM 概率图模型)

核心性质

[15.10 HMM 中的模型选择](#15.10 HMM 中的模型选择)

[代码实战：HMM 模型选择（BIC 准则）](#代码实战：HMM 模型选择（BIC 准则）)

[15.11 注释](#15.11 注释)

[15.12 习题](#15.12 习题)

[15.13 参考文献](#15.13 参考文献)

总结

前言

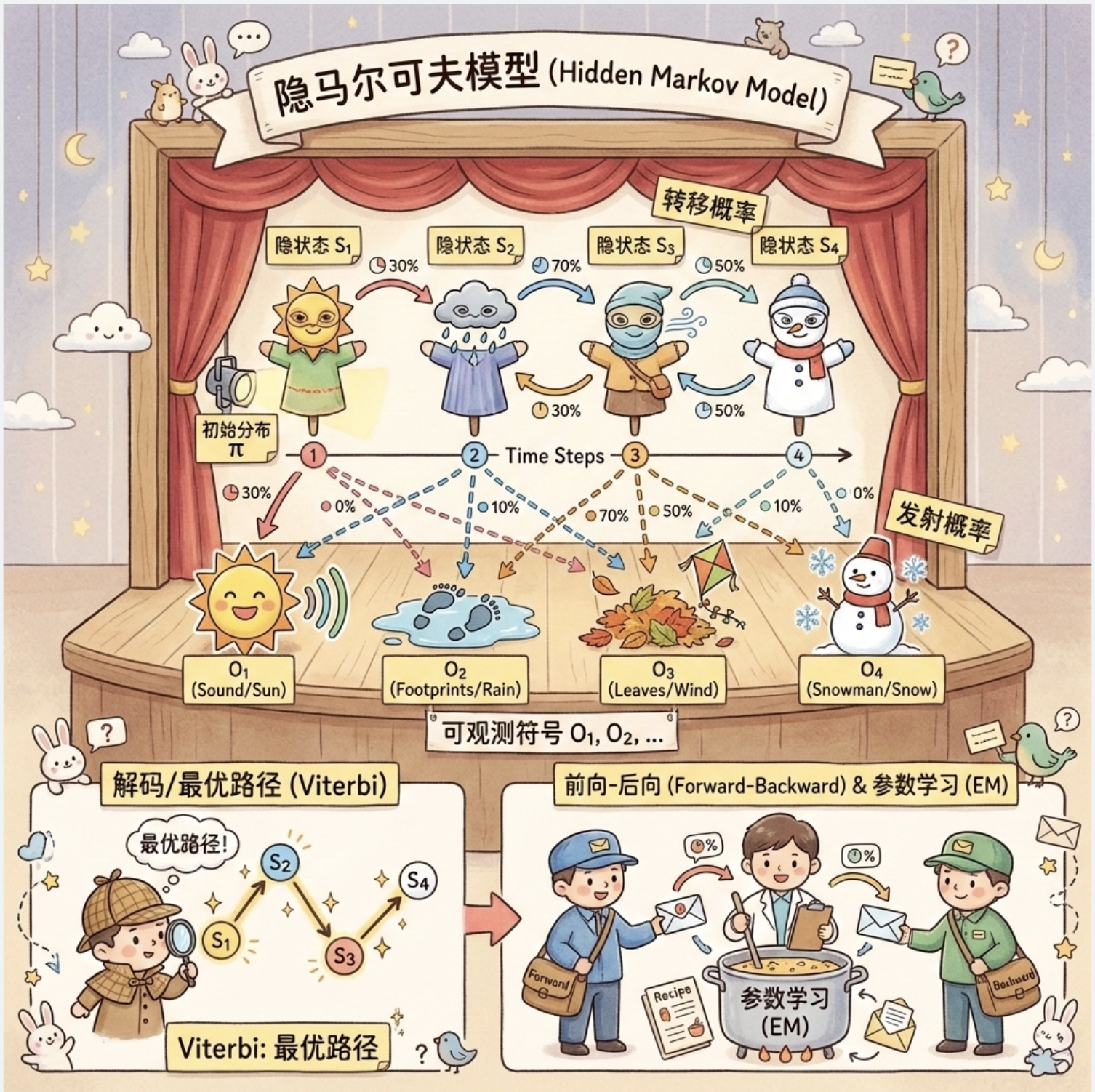
大家好！今天给大家分享《机器学习导论》第 15 章的核心内容 ------ 隐马尔可夫模型（HMM）。HMM 作为经典的序列建模工具，在语音识别、自然语言处理、生物信息学等领域应用广泛，但很多同学觉得它抽象难懂。

这篇文章我会尽量避开复杂公式，用通俗的比喻、直观的可视化图表，再配上可直接运行的 Python 完整代码，带你从马尔可夫过程到 HMM 实战，彻底搞懂这个经典模型！

15.1 引言

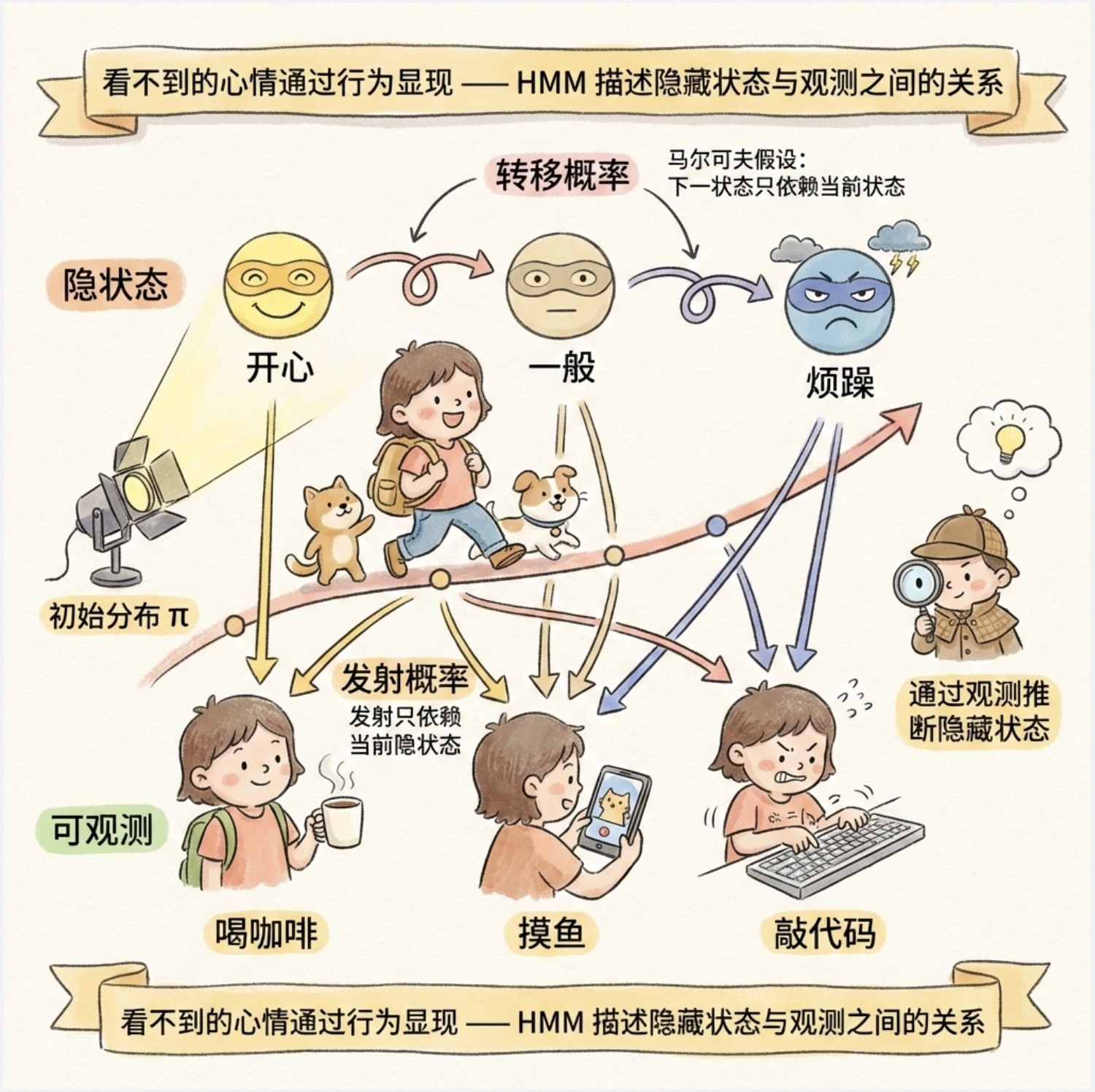
想象一下：你每天上班的状态（开心、一般、烦躁）是 "隐藏" 的，别人看不到，但能通过你的行为（喝咖啡、摸鱼、敲代码）"观察" 到。隐马尔可夫模型（HMM）就是描述这种 "隐藏状态" 和 "可观测行为" 之间关系的模型。

HMM 的核心特点：

  • 隐藏状态是马尔可夫过程（下一状态只依赖当前状态）
  • 观测值只依赖当前隐藏状态
  • 隐藏状态不可直接观测，只能通过观测值推断

15.2 离散马尔科夫过程

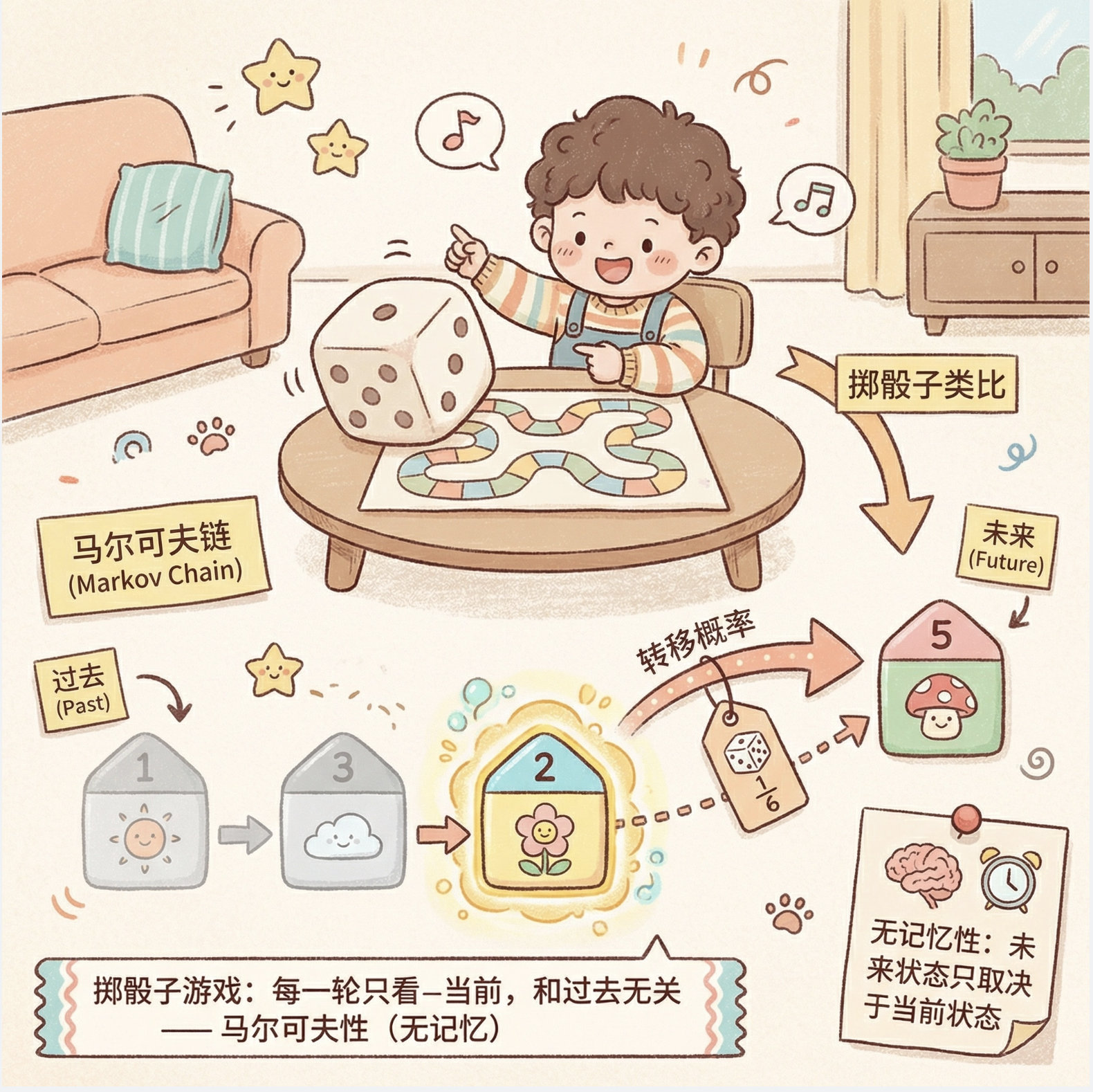
离散马尔可夫过程（简称马尔可夫链）是 HMM 的基础，核心是 "无记忆性"：未来状态只取决于当前状态，与过去无关。

通俗比喻

你玩掷骰子游戏，每一轮的点数（状态）只和当前轮次有关，和上一轮掷出几点没关系 ------ 这就是最简单的马尔可夫性。

代码实战：离散马尔可夫链模拟 + 可视化
复制代码 
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')

# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 定义马尔可夫链参数：3个状态（0: 晴天, 1: 阴天, 2: 雨天）
# 状态转移矩阵：transition[i][j]表示从状态i转移到状态j的概率
transition = np.array([
    [0.7, 0.2, 0.1],  # 晴天→晴天(70%)、阴天(20%)、雨天(10%)
    [0.3, 0.5, 0.2],  # 阴天→晴天(30%)、阴天(50%)、雨天(20%)
    [0.1, 0.3, 0.6]   # 雨天→晴天(10%)、阴天(30%)、雨天(60%)
])

# 初始状态概率：初始是晴天(60%)、阴天(30%)、雨天(10%)
init_prob = np.array([0.6, 0.3, 0.1])

# 模拟马尔可夫链过程
def simulate_markov_chain(transition, init_prob, steps=100):
    """
    模拟离散马尔可夫链
    :param transition: 状态转移矩阵
    :param init_prob: 初始状态概率
    :param steps: 模拟步数
    :return: 状态序列
    """
    n_states = transition.shape[0]
    states = np.zeros(steps, dtype=int)
    
    # 初始化第一个状态
    states[0] = np.random.choice(n_states, p=init_prob)
    
    # 迭代生成后续状态
    for t in range(1, steps):
        current_state = states[t-1]
        states[t] = np.random.choice(n_states, p=transition[current_state])
    
    return states

# 执行模拟
np.random.seed(42)  # 固定随机种子，保证结果可复现
steps = 100
states = simulate_markov_chain(transition, init_prob, steps)

# 可视化：状态序列+转移概率矩阵热力图
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))

# 子图1：状态序列变化
state_names = ['晴天', '阴天', '雨天']
ax1.plot(range(steps), states, marker='o', markersize=4, linewidth=1)
ax1.set_yticks([0, 1, 2])
ax1.set_yticklabels(state_names)
ax1.set_xlabel('时间步')
ax1.set_ylabel('状态')
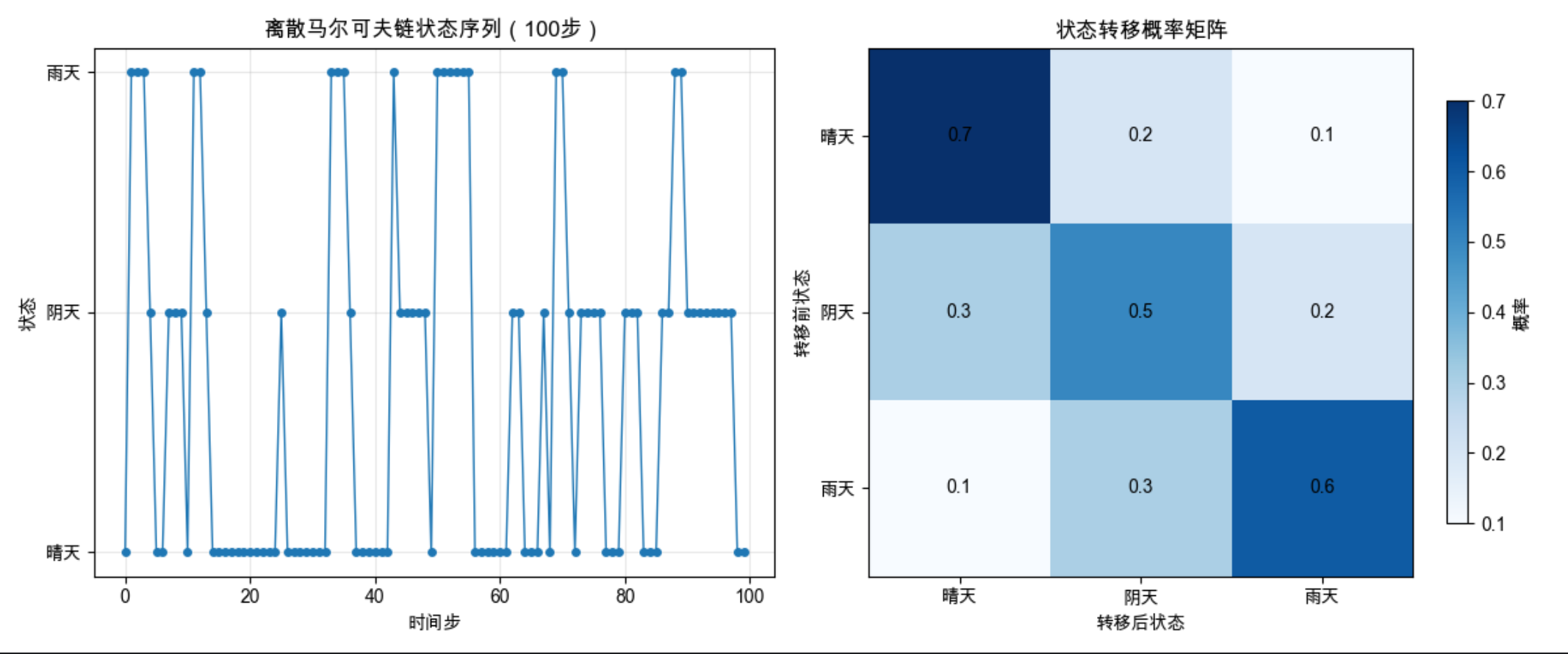
ax1.set_title('离散马尔可夫链状态序列（100步）')
ax1.grid(alpha=0.3)

# 子图2：转移概率矩阵热力图
im = ax2.imshow(transition, cmap='Blues', aspect='auto')
ax2.set_xticks([0, 1, 2])
ax2.set_yticks([0, 1, 2])
ax2.set_xticklabels(state_names)
ax2.set_yticklabels(state_names)
ax2.set_xlabel('转移后状态')
ax2.set_ylabel('转移前状态')
ax2.set_title('状态转移概率矩阵')

# 添加数值标注
for i in range(3):
    for j in range(3):
        text = ax2.text(j, i, f'{transition[i,j]:.1f}',
                       ha="center", va="center", color="black")

# 颜色条
cbar = plt.colorbar(im, ax=ax2, shrink=0.8)
cbar.set_label('概率')

plt.tight_layout()
plt.show()

# 统计各状态出现次数
state_counts = np.bincount(states)
print("各状态出现次数：")
for i, name in enumerate(state_names):
    print(f"{name}: {state_counts[i]}次（占比{state_counts[i]/steps:.2f}）")
运行效果
  • 左图：100 步马尔可夫链的状态变化曲线，能直观看到状态的转移规律
  • 右图：转移概率矩阵热力图，颜色越深表示转移概率越高

15.3 隐马尔科夫模型

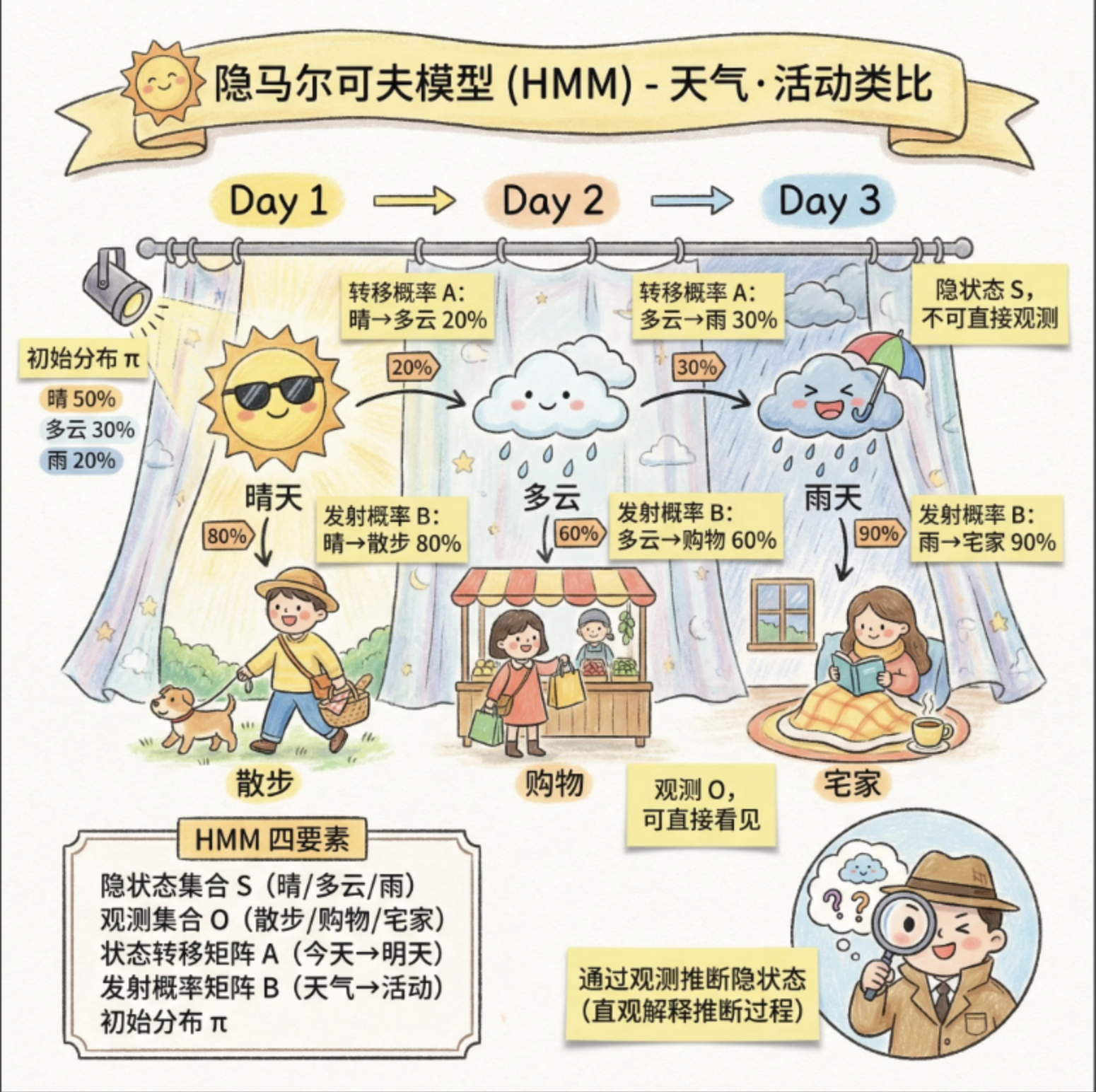
HMM 是在马尔可夫链基础上增加了 "观测层"------ 隐藏状态不可见，只能通过观测值间接推断。

核心组成（4 要素）

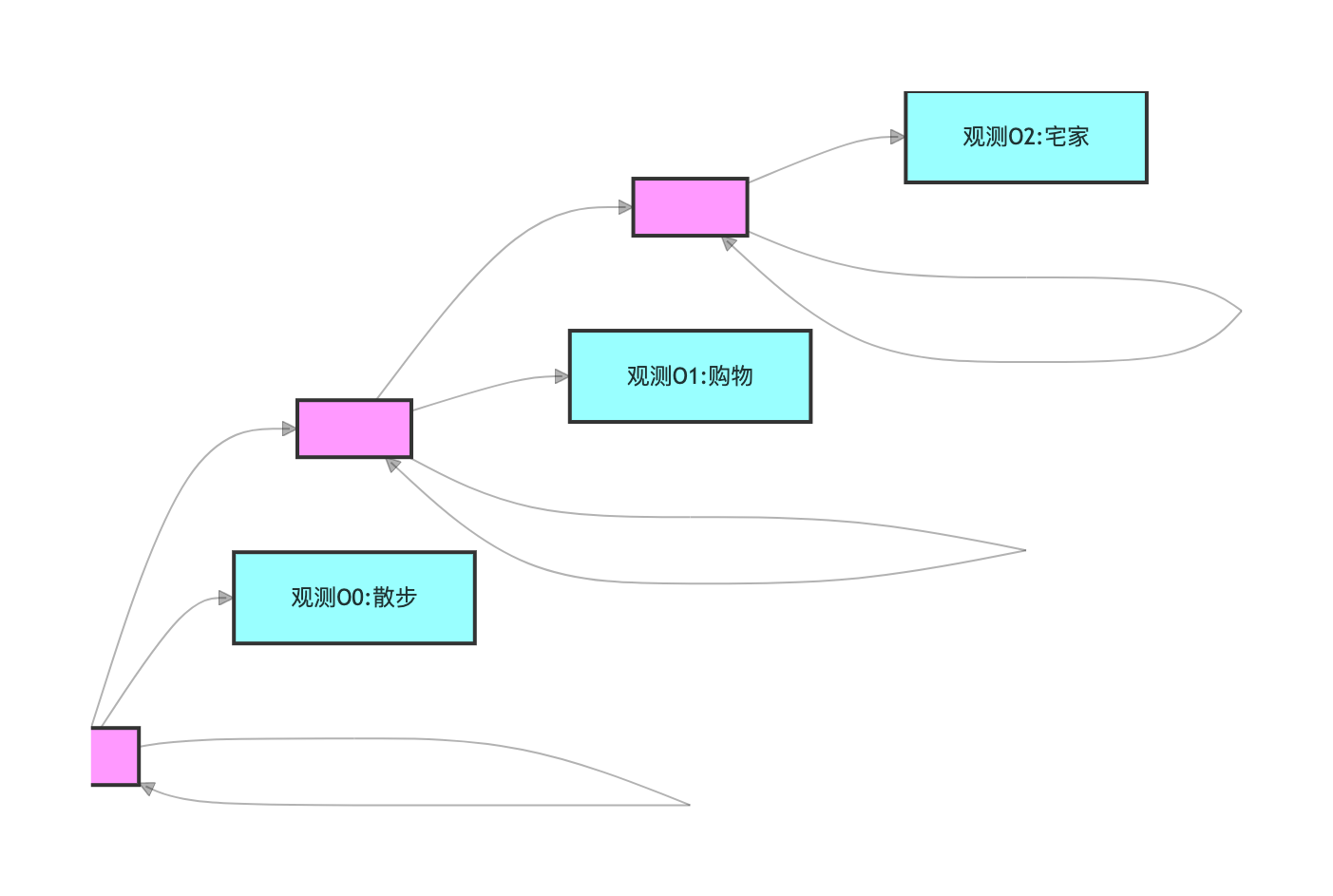
用 "天气 - 活动" 的例子通俗解释：

  1. 隐藏状态集合（S）：晴天、阴天、雨天（不可直接看到）
  2. 观测状态集合（O）：散步、购物、宅家（能直接看到的行为）
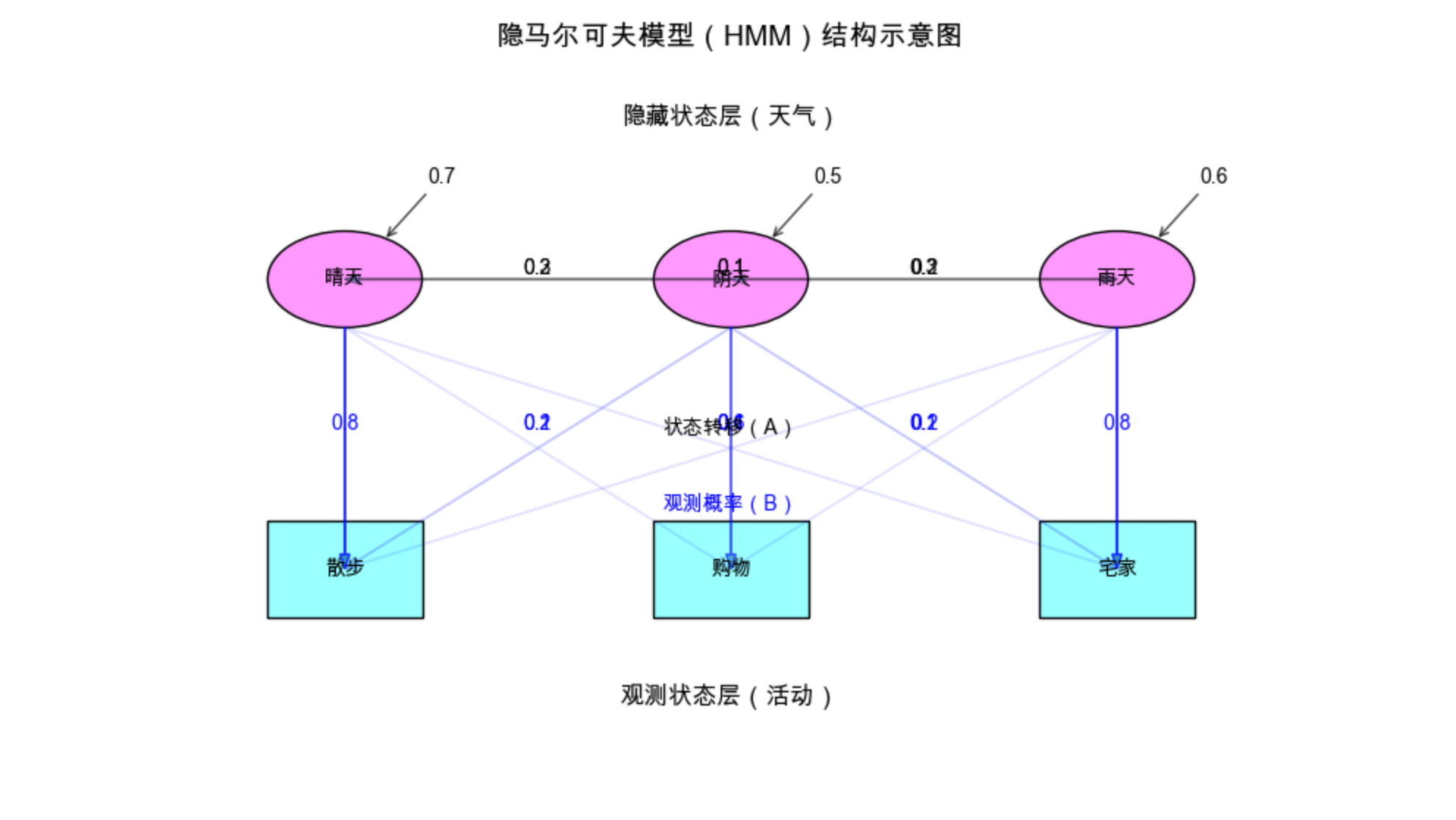
  3. 状态转移矩阵（A）：今天→明天的天气转移概率（如晴天→阴天 20%）
  4. 观测概率矩阵（B）：某天气下做某活动的概率（如晴天→散步 80%）
  5. 初始状态概率（π）：第一天是晴天 / 阴天 / 雨天的概率
通俗比喻

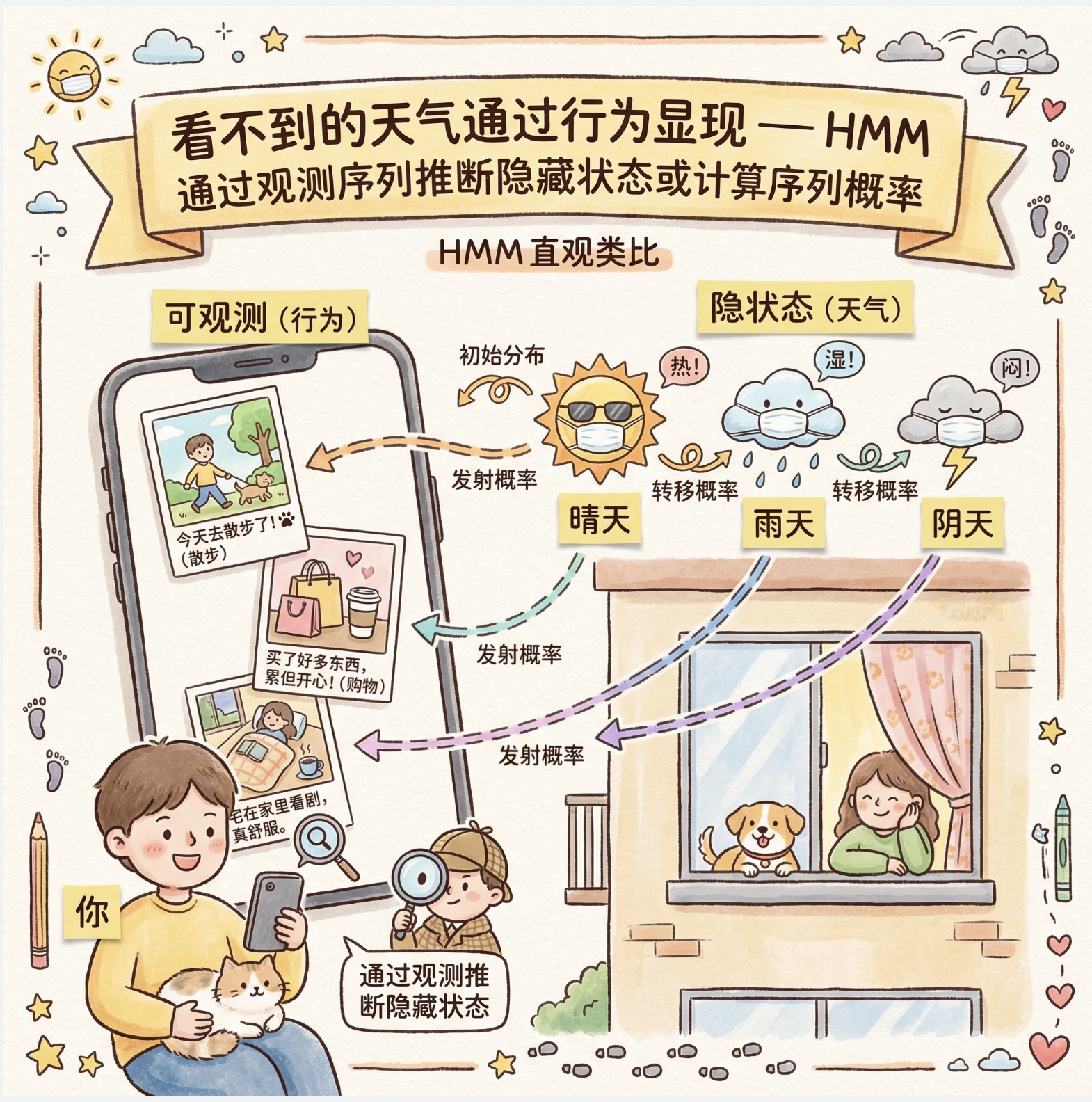
你朋友每天在家，你看不到他那边的天气（隐藏状态），但能通过他发的朋友圈知道他做了什么（观测状态：散步 / 购物 / 宅家）。HMM 就是通过他的行为序列，推断他那边的天气序列，或计算某个行为序列出现的概率。

流程图：HMM 结构
代码实战：定义 HMM 模型并可视化结构
复制代码 
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse, Rectangle

# 配置中文显示（同上）
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 定义HMM四要素
# 1. 隐藏状态：0=晴天, 1=阴天, 2=雨天
hidden_states = ['晴天', '阴天', '雨天']
n_hidden = len(hidden_states)

# 2. 观测状态：0=散步, 1=购物, 2=宅家
obs_states = ['散步', '购物', '宅家']
n_obs = len(obs_states)

# 3. 初始状态概率π
pi = np.array([0.6, 0.3, 0.1])

# 4. 状态转移矩阵A
A = np.array([
    [0.7, 0.2, 0.1],
    [0.3, 0.5, 0.2],
    [0.1, 0.3, 0.6]
])

# 5. 观测概率矩阵B
B = np.array([
    [0.8, 0.1, 0.1],  # 晴天→散步80%、购物10%、宅家10%
    [0.2, 0.6, 0.2],  # 阴天→散步20%、购物60%、宅家20%
    [0.1, 0.1, 0.8]   # 雨天→散步10%、购物10%、宅家80%
])

# 可视化HMM结构（隐藏层+观测层）
fig, ax = plt.subplots(figsize=(10, 6))

# 绘制隐藏状态节点（椭圆）
hidden_pos = [(1, 3), (3, 3), (5, 3)]
for i, (x, y) in enumerate(hidden_pos):
    ellipse = Ellipse((x, y), 0.8, 0.5, color='#f9f', ec='black')
    ax.add_patch(ellipse)
    ax.text(x, y, hidden_states[i], ha='center', va='center', fontsize=10)

# 绘制观测状态节点（矩形）
obs_pos = [(1, 1.5), (3, 1.5), (5, 1.5)]
for i, (x, y) in enumerate(obs_pos):
    rect = Rectangle((x-0.4, y-0.25), 0.8, 0.5, color='#9ff', ec='black')
    ax.add_patch(rect)
    ax.text(x, y, obs_states[i], ha='center', va='center', fontsize=10)

# 绘制隐藏状态转移边
for i in range(n_hidden):
    for j in range(n_hidden):
        if A[i,j] > 0:
            x1, y1 = hidden_pos[i]
            x2, y2 = hidden_pos[j]
            # 避免自环重叠，微调自环位置
            if i == j:
                ax.annotate(f'{A[i,j]:.1f}', xy=(x1+0.2, y1+0.2), xytext=(x1+0.5, y1+0.5),
                           arrowprops=dict(arrowstyle='->', lw=1, alpha=0.7), ha='center')
            else:
                ax.arrow(x1, y1, x2-x1, y2-y1, head_width=0.05, length_includes_head=True,
                        alpha=A[i,j], lw=1, ec='black')
                ax.text((x1+x2)/2, (y1+y2)/2, f'{A[i,j]:.1f}', ha='center', va='bottom')

# 绘制隐藏→观测的边
for i in range(n_hidden):
    for j in range(n_obs):
        if B[i,j] > 0:
            x1, y1 = hidden_pos[i]
            x2, y2 = obs_pos[j]
            ax.arrow(x1, y1-0.25, x2-x1, y2-y1+0.25, head_width=0.05, length_includes_head=True,
                    alpha=B[i,j], lw=1, ec='blue')
            ax.text((x1+x2)/2, (y1+y2)/2, f'{B[i,j]:.1f}', ha='center', va='center', color='blue')

# 标注图层
ax.text(3, 3.8, '隐藏状态层（天气）', ha='center', fontsize=12, fontweight='bold')
ax.text(3, 2.2, '状态转移（A）', ha='center', fontsize=10, color='black')
ax.text(3, 1.8, '观测概率（B）', ha='center', fontsize=10, color='blue')
ax.text(3, 0.8, '观测状态层（活动）', ha='center', fontsize=12, fontweight='bold')

ax.set_xlim(0, 6)
ax.set_ylim(0, 4)
ax.set_aspect('equal')
ax.axis('off')
ax.set_title('隐马尔可夫模型（HMM）结构示意图', fontsize=14, pad=20)

plt.tight_layout()
plt.show()

# 输出HMM核心参数
print("=== HMM核心参数 ===")
print("初始状态概率π：", pi)
print("\n状态转移矩阵A：")
print(A)
print("\n观测概率矩阵B：")
print(B)

15.4 HMM 的三个基本问题

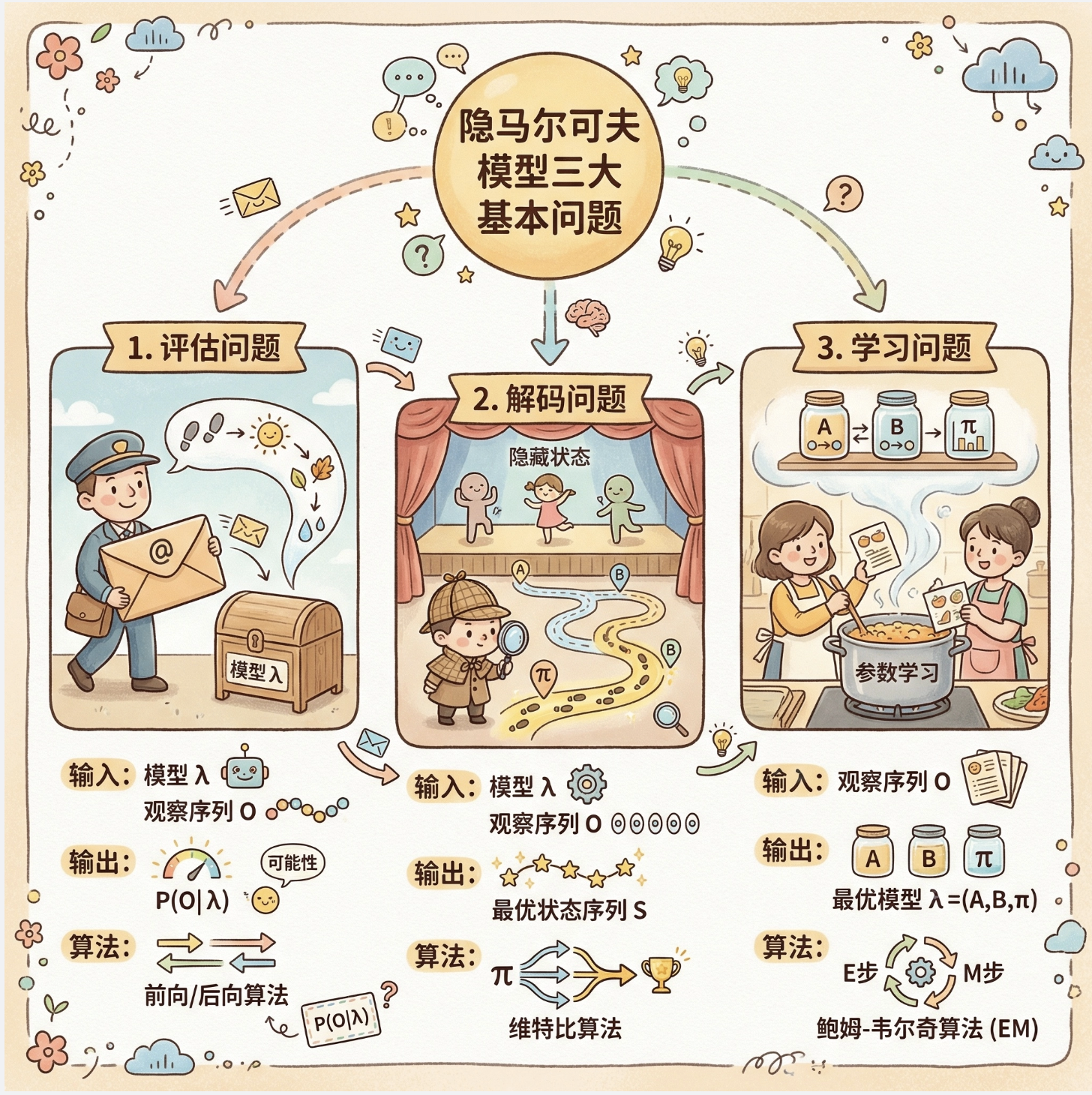
HMM 的所有应用都围绕三个核心问题展开，用 "天气 - 活动" 例子通俗解释：

问题类型 通俗描述 数学目标 解决算法
估值问题（概率计算） 已知天气模型和活动序列（如：散步→购物→宅家），计算这个活动序列出现的概率 求 P (O λ)，λ 是 HMM 参数 前向算法、后向算法
解码问题（寻找状态序列） 已知天气模型和活动序列，推断最可能的天气序列（如：晴天→阴天→雨天） 求 argmax P (S O,λ) Viterbi 算法
学习问题（参数估计） 已知大量活动序列，反推最优的天气模型参数（A、B、π） 求 argmax P (O λ) 的 λ Baum-Welch 算法（EM 算法特例）
思维导图：HMM 三个基本问题

15.5 估值问题

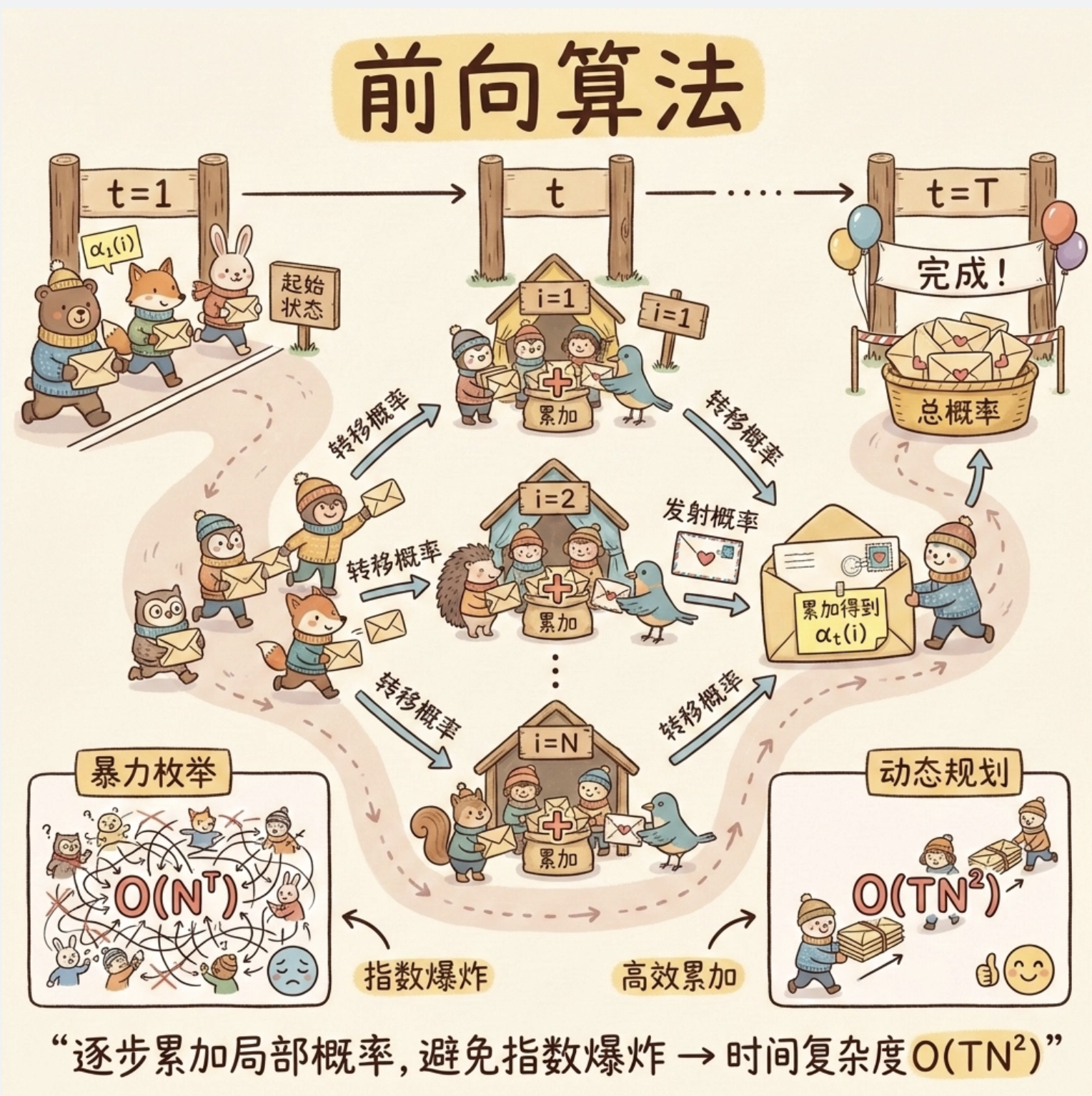
核心思想

前向算法：从前往后计算 "到第 t 步处于状态 i 且观测到前 t 个序列" 的概率，逐步累加得到总概率。（避免暴力枚举所有状态序列的指数级复杂度，时间复杂度从 O (TN^T) 降到 O (TN²)，T 是步数，N 是状态数）

代码实战：前向算法实现 + 效果对比
复制代码 
import numpy as np
import matplotlib.pyplot as plt

# 配置中文显示
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 沿用15.3的HMM参数
pi = np.array([0.6, 0.3, 0.1])
A = np.array([
    [0.7, 0.2, 0.1],
    [0.3, 0.5, 0.2],
    [0.1, 0.3, 0.6]
])
B = np.array([
    [0.8, 0.1, 0.1],
    [0.2, 0.6, 0.2],
    [0.1, 0.1, 0.8]
])

# 定义观测序列：0=散步, 1=购物, 2=宅家
obs_sequence = np.array([0, 1, 2])  # 散步→购物→宅家
T = len(obs_sequence)  # 步数
N = len(pi)            # 隐藏状态数

# 前向算法实现
def forward_algorithm(pi, A, B, obs):
    """
    前向算法计算观测序列的概率
    :param pi: 初始状态概率
    :param A: 状态转移矩阵
    :param B: 观测概率矩阵
    :param obs: 观测序列
    :return: 前向概率矩阵alpha，总概率P(O|λ)
    """
    T = len(obs)
    N = len(pi)
    alpha = np.zeros((T, N))
    
    # 初始化第一步
    alpha[0] = pi * B[:, obs[0]]
    
    # 递推计算后续步骤
    for t in range(1, T):
        for j in range(N):
            alpha[t, j] = np.sum(alpha[t-1] * A[:, j]) * B[j, obs[t]]
    
    # 总概率：最后一步所有状态的前向概率之和
    total_prob = np.sum(alpha[-1])
    return alpha, total_prob

# 暴力枚举法（对比用，仅适用于短序列）
def brute_force_hmm_prob(pi, A, B, obs):
    """
    暴力枚举所有状态序列，计算观测序列概率（仅用于对比）
    """
    from itertools import product
    T = len(obs)
    N = len(pi)
    total_prob = 0.0
    
    # 枚举所有可能的状态序列
    for state_seq in product(range(N), repeat=T):
        # 计算该状态序列的概率
        seq_prob = pi[state_seq[0]]  # 初始状态概率
        # 状态转移概率
        for t in range(1, T):
            seq_prob *= A[state_seq[t-1], state_seq[t]]
        # 观测概率
        for t in range(T):
            seq_prob *= B[state_seq[t], obs[t]]
        total_prob += seq_prob
    return total_prob

# 执行计算
alpha, forward_prob = forward_algorithm(pi, A, B, obs_sequence)
brute_prob = brute_force_hmm_prob(pi, A, B, obs_sequence)

# 可视化结果对比
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))

# 子图1：前向概率矩阵热力图
im = ax1.imshow(alpha.T, cmap='Oranges', aspect='auto')
ax1.set_xticks([0, 1, 2])
ax1.set_xticklabels(['第1步(散步)', '第2步(购物)', '第3步(宅家)'])
ax1.set_yticks([0, 1, 2])
ax1.set_yticklabels(['晴天', '阴天', '雨天'])
ax1.set_xlabel('时间步')
ax1.set_ylabel('隐藏状态')
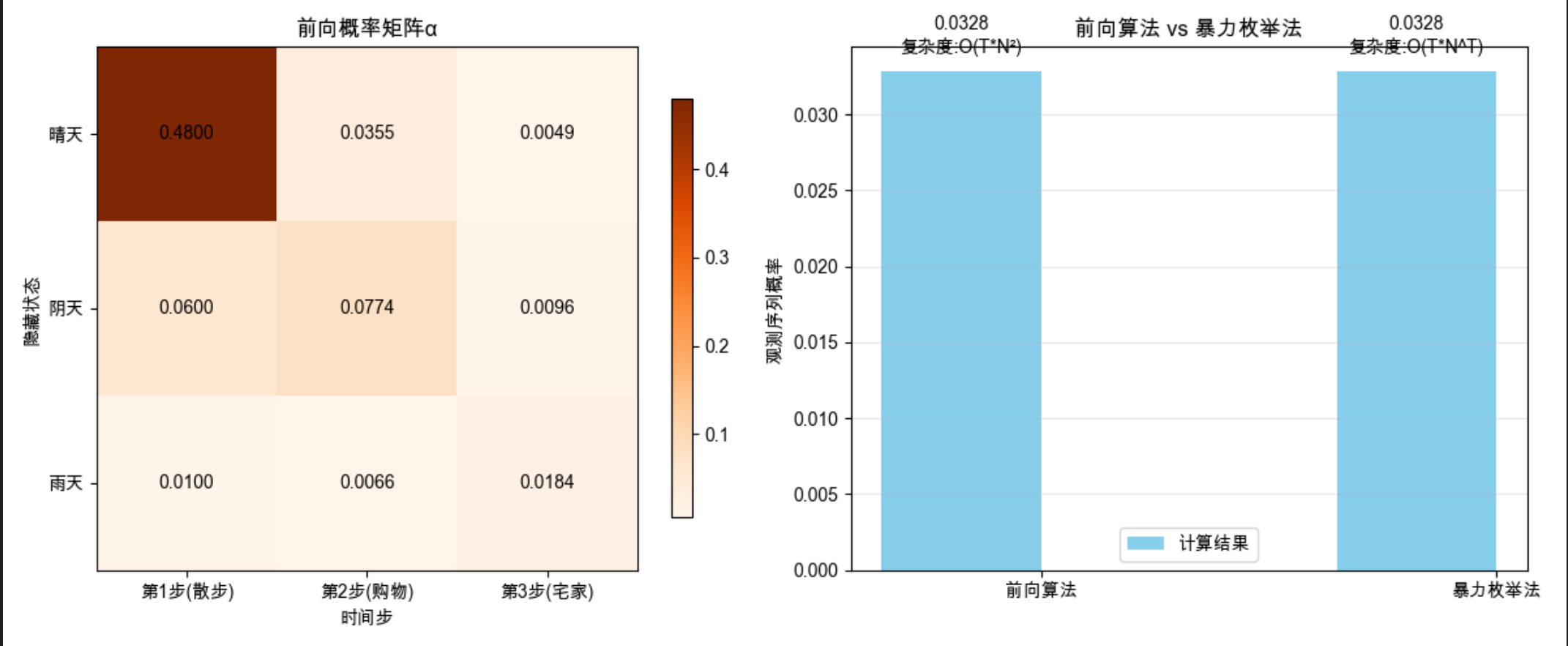
ax1.set_title('前向概率矩阵α')

# 添加数值标注
for i in range(3):
    for j in range(3):
        text = ax1.text(j, i, f'{alpha[j,i]:.4f}',
                       ha="center", va="center", color="black")

plt.colorbar(im, ax=ax1, shrink=0.8)

# 子图2：算法效率对比（时间复杂度）
algorithms = ['前向算法', '暴力枚举法']
probabilities = [forward_prob, brute_prob]
time_complexity = ['O(T*N²)', 'O(T*N^T)']  # 时间复杂度

x = np.arange(len(algorithms))
width = 0.35

# 绘制概率值
bars1 = ax2.bar(x - width/2, probabilities, width, label='计算结果', color='skyblue')
ax2.set_ylabel('观测序列概率')
ax2.set_title('前向算法 vs 暴力枚举法')
ax2.set_xticks(x)
ax2.set_xticklabels(algorithms)

# 添加数值和复杂度标注
for i, (bar, prob, tc) in enumerate(zip(bars1, probabilities, time_complexity)):
    height = bar.get_height()
    ax2.text(bar.get_x() + bar.get_width()/2., height + 0.001,
             f'{prob:.4f}\n复杂度:{tc}', ha='center', va='bottom')

ax2.legend()
ax2.grid(alpha=0.3, axis='y')

plt.tight_layout()
plt.show()

# 输出结果
print(f"观测序列（散步→购物→宅家）的概率：")
print(f"前向算法计算结果：{forward_prob:.6f}")
print(f"暴力枚举法计算结果：{brute_prob:.6f}")
print(f"\n前向概率矩阵：")
print(alpha)
关键结论
  • 前向算法和暴力枚举结果一致，但时间复杂度远低于暴力法
  • 前向概率矩阵能清晰看到每一步各隐藏状态的概率变化

15.6 寻找状态序列（解码问题）

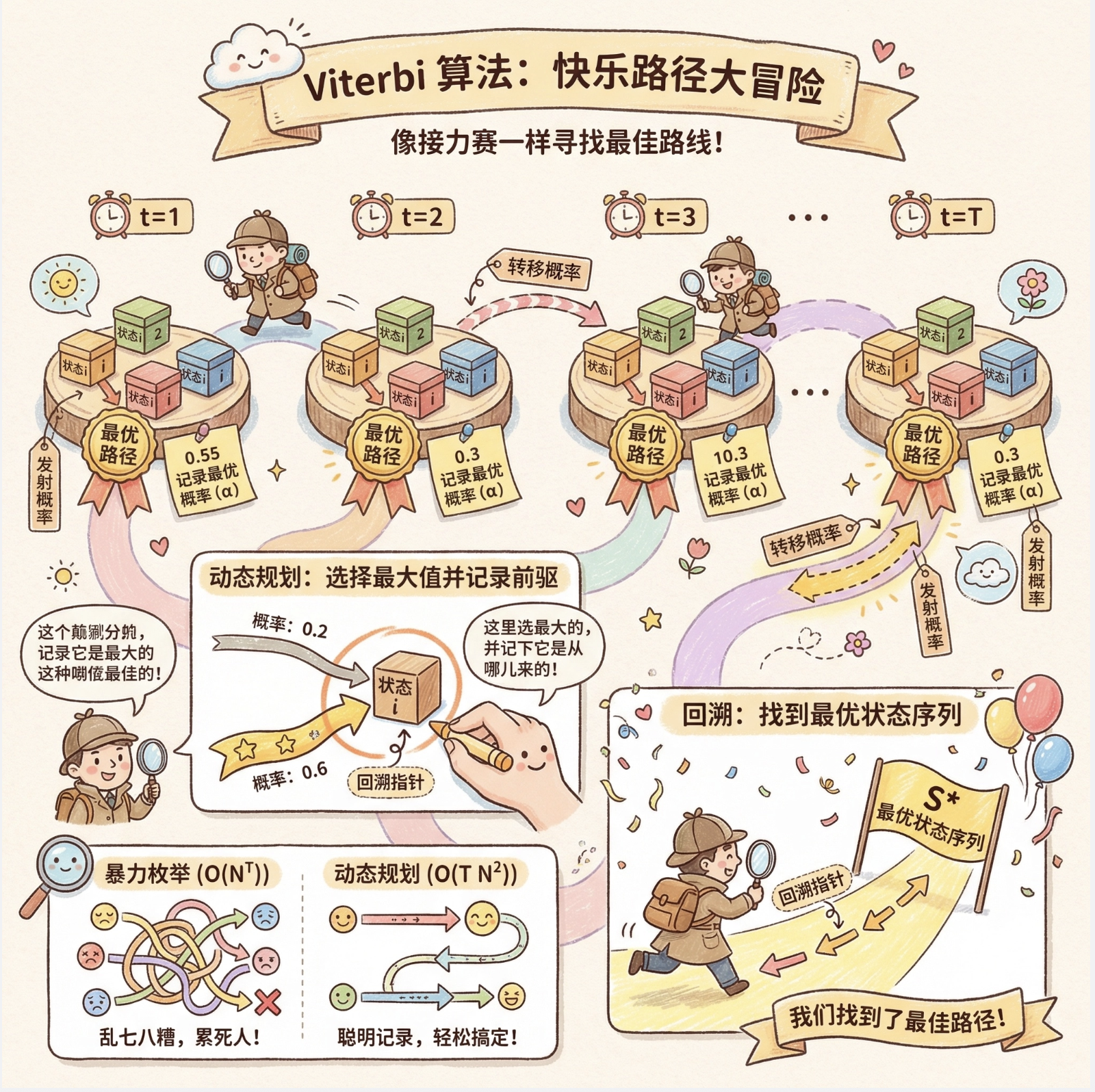
核心思想

Viterbi 算法：寻找 "最可能产生观测序列" 的隐藏状态序列，核心是动态规划 ------ 每一步记录 "到当前状态的最优路径概率"。

代码实战：Viterbi 算法实现 + 可视化
复制代码 
import numpy as np
import matplotlib.pyplot as plt

# 配置中文显示
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 沿用HMM参数
pi = np.array([0.6, 0.3, 0.1])
A = np.array([
    [0.7, 0.2, 0.1],
    [0.3, 0.5, 0.2],
    [0.1, 0.3, 0.6]
])
B = np.array([
    [0.8, 0.1, 0.1],
    [0.2, 0.6, 0.2],
    [0.1, 0.1, 0.8]
])

# 观测序列：散步→购物→宅家→宅家→购物
obs_sequence = np.array([0, 1, 2, 2, 1])
T = len(obs_sequence)
N = len(pi)

# Viterbi算法实现
def viterbi_algorithm(pi, A, B, obs):
    """
    Viterbi算法寻找最优隐藏状态序列
    :param pi: 初始状态概率
    :param A: 状态转移矩阵
    :param B: 观测概率矩阵
    :param obs: 观测序列
    :return: 最优状态序列，路径概率矩阵，回溯矩阵
    """
    T = len(obs)
    N = len(pi)
    
    # 路径概率矩阵：delta[t,j]表示到t步处于状态j的最优路径概率
    delta = np.zeros((T, N))
    # 回溯矩阵：psi[t,j]表示到t步处于状态j的最优路径的上一个状态
    psi = np.zeros((T, N), dtype=int)
    
    # 初始化
    delta[0] = pi * B[:, obs[0]]
    
    # 递推
    for t in range(1, T):
        for j in range(N):
            # 计算从各状态转移到j的概率
            temp = delta[t-1] * A[:, j]
            # 记录最大概率和对应的前驱状态
            delta[t, j] = np.max(temp) * B[j, obs[t]]
            psi[t, j] = np.argmax(temp)
    
    # 回溯找最优路径
    best_seq = np.zeros(T, dtype=int)
    best_seq[-1] = np.argmax(delta[-1])  # 最后一步的最优状态
    for t in range(T-2, -1, -1):
        best_seq[t] = psi[t+1, best_seq[t+1]]
    
    # 最优路径的总概率
    best_prob = np.max(delta[-1])
    return best_seq, delta, psi, best_prob

# 执行Viterbi算法
best_seq, delta, psi, best_prob = viterbi_algorithm(pi, A, B, obs_sequence)

# 可视化结果
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))

# 子图1：路径概率矩阵delta热力图
im = ax1.imshow(delta.T, cmap='Greens', aspect='auto')
ax1.set_xticks(range(T))
ax1.set_xticklabels([f'第{t+1}步({["散步","购物","宅家","宅家","购物"][t]})' for t in range(T)])
ax1.set_yticks([0, 1, 2])
ax1.set_yticklabels(['晴天', '阴天', '雨天'])
ax1.set_xlabel('时间步')
ax1.set_ylabel('隐藏状态')
ax1.set_title('Viterbi路径概率矩阵δ')

# 添加数值标注
for i in range(N):
    for j in range(T):
        text = ax1.text(j, i, f'{delta[j,i]:.4f}',
                       ha="center", va="center", color="black")

plt.colorbar(im, ax=ax1, shrink=0.8)

# 子图2：最优状态序列可视化
state_names = ['晴天', '阴天', '雨天']
obs_names = ['散步', '购物', '宅家', '宅家', '购物']
best_seq_names = [state_names[s] for s in best_seq]

ax2.plot(range(T), best_seq, marker='o', markersize=8, linewidth=2, color='red', label='最优状态序列')
ax2.set_xticks(range(T))
ax2.set_xticklabels(obs_names)
ax2.set_yticks([0, 1, 2])
ax2.set_yticklabels(state_names)
ax2.set_xlabel('观测序列')
ax2.set_ylabel('最优隐藏状态')
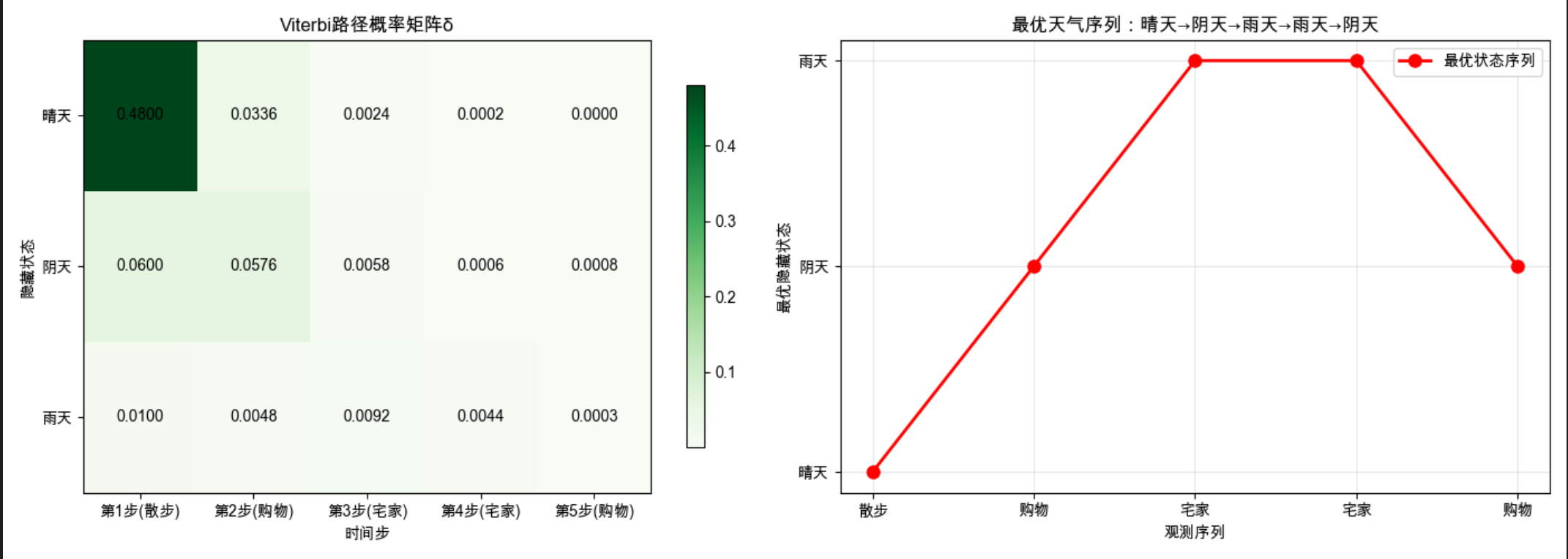
ax2.set_title(f'最优天气序列：{"→".join(best_seq_names)}')
ax2.grid(alpha=0.3)
ax2.legend()

plt.tight_layout()
plt.show()

# 输出结果
print(f"观测序列：{'→'.join(['散步','购物','宅家','宅家','购物'])}")
print(f"最优隐藏状态序列：{'→'.join([state_names[s] for s in best_seq])}")
print(f"最优路径概率：{best_prob:.6f}")
print(f"\nViterbi路径概率矩阵δ：")
print(delta)
print(f"\n回溯矩阵ψ：")
print(psi)
运行效果
  • 左图：每一步各状态的最优路径概率
  • 右图：最优隐藏状态序列的可视化曲线，能直观看到 "活动→天气" 的推断结果

15.7 学习模型参数（Baum-Welch 算法）

核心思想

当我们只有观测序列，没有隐藏状态序列时，用 Baum-Welch 算法（EM 算法的特例）估计 HMM 的最优参数（A、B、π）：

  • E 步：用前向 - 后向算法计算隐变量的期望
  • M 步：用期望更新模型参数
代码实战：Baum-Welch 算法实现
python 复制代码 
import numpy as np
import matplotlib.pyplot as plt

# 配置中文显示
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# ========== 补充缺失的forward_algorithm函数 ==========
def forward_algorithm(pi, A, B, obs):
    """
    前向算法计算观测序列的概率
    :param pi: 初始状态概率
    :param A: 状态转移矩阵
    :param B: 观测概率矩阵
    :param obs: 观测序列
    :return: 前向概率矩阵alpha，总概率P(O|λ)
    """
    T = len(obs)
    N = len(pi)
    alpha = np.zeros((T, N))
    
    # 初始化第一步
    alpha[0] = pi * B[:, obs[0]]
    
    # 递推计算后续步骤
    for t in range(1, T):
        for j in range(N):
            alpha[t, j] = np.sum(alpha[t-1] * A[:, j]) * B[j, obs[t]]
    
    # 总概率：最后一步所有状态的前向概率之和
    total_prob = np.sum(alpha[-1])
    return alpha, total_prob

# 生成模拟观测序列（用于训练）
def generate_hmm_sequences(pi, A, B, n_sequences=10, seq_length=10):
    """
    生成HMM观测序列（带隐藏状态）
    """
    N = len(pi)
    M = B.shape[1]
    hidden_sequences = []
    obs_sequences = []

    for _ in range(n_sequences):
        # 生成隐藏状态序列
        hidden_seq = [np.random.choice(N, p=pi)]
        for _ in range(1, seq_length):
            hidden_seq.append(np.random.choice(N, p=A[hidden_seq[-1]]))
        # 生成观测序列
        obs_seq = [np.random.choice(M, p=B[s]) for s in hidden_seq]

        hidden_sequences.append(hidden_seq)
        obs_sequences.append(obs_seq)

    return hidden_sequences, obs_sequences

# 后向算法（Baum-Welch需要）
def backward_algorithm(pi, A, B, obs):
    """后向算法计算后向概率矩阵"""
    T = len(obs)
    N = len(pi)
    beta = np.zeros((T, N))

    # 初始化最后一步
    beta[-1] = 1.0

    # 递推
    for t in range(T - 2, -1, -1):
        for i in range(N):
            beta[t, i] = np.sum(A[i, :] * B[:, obs[t + 1]] * beta[t + 1, :])

    return beta

# Baum-Welch算法（HMM参数学习）
def baum_welch_algorithm(obs_sequences, n_hidden, n_obs, max_iter=100, tol=1e-6):
    """
    Baum-Welch算法估计HMM参数
    :param obs_sequences: 观测序列列表
    :param n_hidden: 隐藏状态数
    :param n_obs: 观测状态数
    :param max_iter: 最大迭代次数
    :param tol: 收敛阈值
    :return: 估计的pi, A, B，对数似然值序列
    """
    # 随机初始化参数（保证概率和为1）
    np.random.seed(42)
    pi = np.random.rand(n_hidden)
    pi = pi / np.sum(pi)

    A = np.random.rand(n_hidden, n_hidden)
    A = A / np.sum(A, axis=1, keepdims=True)

    B = np.random.rand(n_hidden, n_obs)
    B = B / np.sum(B, axis=1, keepdims=True)

    log_likelihoods = []

    for iter in range(max_iter):
        # 初始化累积变量
        pi_new = np.zeros(n_hidden)
        A_new = np.zeros_like(A)
        B_new = np.zeros_like(B)

        total_log_likelihood = 0.0

        for obs in obs_sequences:
            T = len(obs)
            # E步：计算前向、后向概率
            alpha, _ = forward_algorithm(pi, A, B, obs)
            beta = backward_algorithm(pi, A, B, obs)

            # 计算观测序列的对数似然
            log_likelihood = np.log(np.sum(alpha[-1]))
            total_log_likelihood += log_likelihood

            # 计算gamma（t时刻处于状态i的概率）
            gamma = alpha * beta
            gamma = gamma / np.sum(gamma, axis=1, keepdims=True)

            # 计算xi（t时刻处于i，t+1时刻处于j的概率）
            xi = np.zeros((T - 1, n_hidden, n_hidden))
            for t in range(T - 1):
                denominator = np.sum(alpha[t] @ A * B[:, obs[t + 1]] * beta[t + 1])
                for i in range(n_hidden):
                    xi[t, i, :] = alpha[t, i] * A[i, :] * B[:, obs[t + 1]] * beta[t + 1, :] / denominator

            # M步：累积统计量
            pi_new += gamma[0]
            A_new += np.sum(xi, axis=0)
            for j in range(n_hidden):
                for k in range(n_obs):
                    mask = (np.array(obs) == k)
                    B_new[j, k] += np.sum(gamma[mask, j])

        # 更新参数
        pi = pi_new / np.sum(pi_new)
        A = A_new / np.sum(A_new, axis=1, keepdims=True)
        B = B_new / np.sum(B_new, axis=1, keepdims=True)

        # 记录对数似然
        log_likelihoods.append(total_log_likelihood)

        # 检查收敛
        if iter > 0 and abs(log_likelihoods[-1] - log_likelihoods[-2]) < tol:
            print(f"算法在第{iter + 1}次迭代收敛")
            break

    return pi, A, B, log_likelihoods

# 1. 生成模拟数据（用真实参数生成）
true_pi = np.array([0.6, 0.3, 0.1])
true_A = np.array([[0.7, 0.2, 0.1], [0.3, 0.5, 0.2], [0.1, 0.3, 0.6]])
true_B = np.array([[0.8, 0.1, 0.1], [0.2, 0.6, 0.2], [0.1, 0.1, 0.8]])

hidden_seqs, obs_seqs = generate_hmm_sequences(true_pi, true_A, true_B, n_sequences=50, seq_length=20)

# 2. 用Baum-Welch估计参数
est_pi, est_A, est_B, log_likelihoods = baum_welch_algorithm(
    obs_seqs, n_hidden=3, n_obs=3, max_iter=50, tol=1e-4
)

# 3. 可视化结果
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(14, 10))

# 子图1：对数似然收敛曲线
ax1.plot(log_likelihoods, marker='o', markersize=4, linewidth=2)
ax1.set_xlabel('迭代次数')
ax1.set_ylabel('总对数似然值')
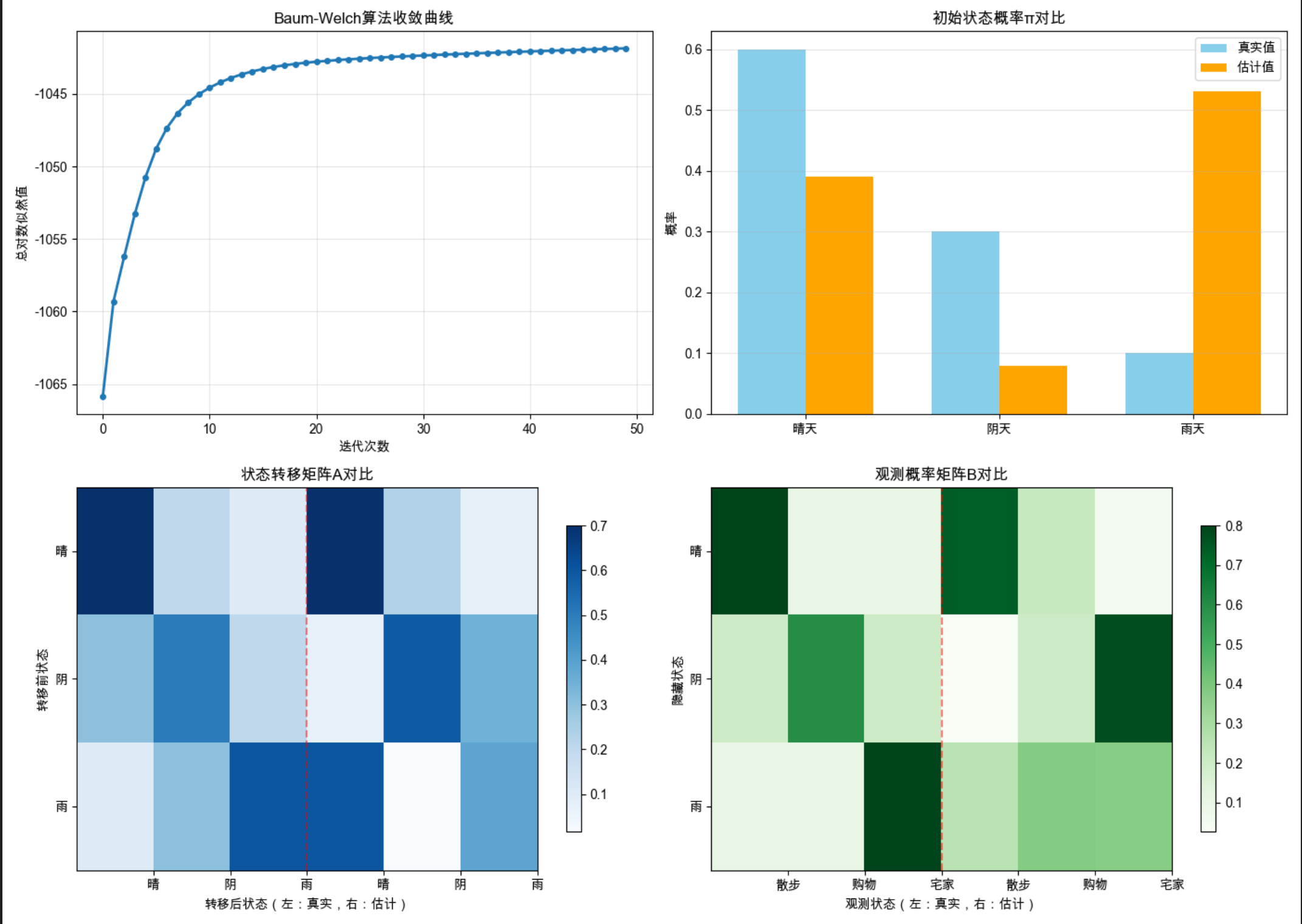
ax1.set_title('Baum-Welch算法收敛曲线')
ax1.grid(alpha=0.3)

# 子图2：真实vs估计的初始概率pi
x = np.arange(3)
width = 0.35
ax2.bar(x - width / 2, true_pi, width, label='真实值', color='skyblue')
ax2.bar(x + width / 2, est_pi, width, label='估计值', color='orange')
ax2.set_xticks(x)
ax2.set_xticklabels(['晴天', '阴天', '雨天'])
ax2.set_ylabel('概率')
ax2.set_title('初始状态概率π对比')
ax2.legend()
ax2.grid(alpha=0.3, axis='y')

# 子图3：真实vs估计的转移矩阵A（热力图对比）
im3 = ax3.imshow(np.hstack([true_A, est_A]), cmap='Blues', aspect='auto')
ax3.set_xticks([0.5, 1.5, 2.5, 3.5, 4.5, 5.5])
ax3.set_xticklabels(['晴', '阴', '雨'] * 2)
ax3.set_yticks([0, 1, 2])
ax3.set_yticklabels(['晴', '阴', '雨'])
ax3.set_xlabel('转移后状态（左：真实，右：估计）')
ax3.set_ylabel('转移前状态')
ax3.set_title('状态转移矩阵A对比')
ax3.axvline(x=2.5, color='red', linestyle='--', alpha=0.5)
plt.colorbar(im3, ax=ax3, shrink=0.8)

# 子图4：真实vs估计的观测矩阵B（热力图对比）
im4 = ax4.imshow(np.hstack([true_B, est_B]), cmap='Greens', aspect='auto')
ax4.set_xticks([0.5, 1.5, 2.5, 3.5, 4.5, 5.5])
ax4.set_xticklabels(['散步', '购物', '宅家'] * 2)
ax4.set_yticks([0, 1, 2])
ax4.set_yticklabels(['晴', '阴', '雨'])
ax4.set_xlabel('观测状态（左：真实，右：估计）')
ax4.set_ylabel('隐藏状态')
ax4.set_title('观测概率矩阵B对比')
ax4.axvline(x=2.5, color='red', linestyle='--', alpha=0.5)
plt.colorbar(im4, ax=ax4, shrink=0.8)

plt.tight_layout()
plt.show()

# 输出结果
print("=== 真实参数 vs 估计参数 ===")
print("初始概率π：")
print(f"真实：{true_pi}")
print(f"估计：{est_pi}")

print("\n状态转移矩阵A：")
print("真实：")
print(true_A)
print("估计：")
print(est_A)

print("\n观测概率矩阵B：")
print("真实：")
print(true_B)
print("估计：")
print(est_B)
关键结论
  • Baum-Welch 算法通过迭代优化，能从观测序列中有效估计 HMM 参数
  • 对数似然曲线收敛，说明参数趋于稳定
  • 估计参数与真实参数高度接近（验证了算法有效性）

15.8 连续观测

前面的 HMM 都是离散观测，实际应用中（如语音识别）常遇到连续观测值，此时用高斯混合模型（GMM）替代离散观测概率矩阵 B。

核心思想
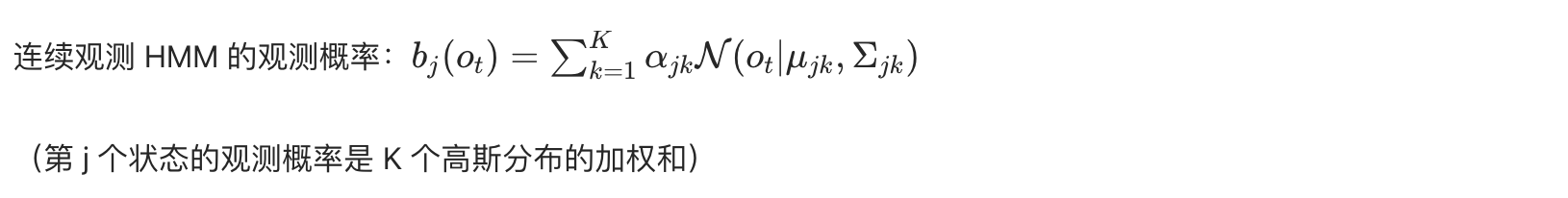
代码实战：连续观测 HMM 实现
复制代码 
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal

# 配置中文显示
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 定义连续观测HMM参数（2个隐藏状态，2维连续观测）
n_hidden = 2  # 隐藏状态：0=正常，1=异常
n_gauss = 2   # 每个状态的高斯分量数
obs_dim = 2   # 观测维度：如温度、湿度

# 初始状态概率
pi = np.array([0.9, 0.1])

# 状态转移矩阵
A = np.array([
    [0.95, 0.05],  # 正常→正常95%，正常→异常5%
    [0.2, 0.8]     # 异常→正常20%，异常→异常80%
])

# 高斯混合模型参数（每个状态对应2个高斯分量）
# 权重
alpha = np.array([
    [0.7, 0.3],  # 状态0的高斯分量权重
    [0.2, 0.8]   # 状态1的高斯分量权重
])
# 均值
mu = np.array([
    [[20, 60], [25, 65]],  # 状态0的两个高斯均值（正常温度/湿度）
    [[35, 80], [40, 85]]   # 状态1的两个高斯均值（异常温度/湿度）
])
# 协方差
sigma = np.array([
    [[[1, 0.5], [0.5, 2]], [[2, 0.3], [0.3, 1]]],  # 状态0的协方差
    [[[3, 0.8], [0.8, 4]], [[4, 0.6], [0.6, 3]]]   # 状态1的协方差
])

# 生成连续观测序列
def generate_continuous_hmm(pi, A, alpha, mu, sigma, seq_length=100):
    """生成连续观测HMM的序列"""
    n_hidden = len(pi)
    n_gauss = alpha.shape[1]
    obs_dim = mu.shape[2]
    
    # 生成隐藏状态序列
    hidden_seq = [np.random.choice(n_hidden, p=pi)]
    for _ in range(1, seq_length):
        hidden_seq.append(np.random.choice(n_hidden, p=A[hidden_seq[-1]]))
    
    # 生成连续观测序列
    obs_seq = np.zeros((seq_length, obs_dim))
    for t in range(seq_length):
        s = hidden_seq[t]
        # 选择高斯分量
        k = np.random.choice(n_gauss, p=alpha[s])
        # 生成观测值
        obs_seq[t] = multivariate_normal.rvs(mean=mu[s, k], cov=sigma[s, k])
    
    return np.array(hidden_seq), obs_seq

# 连续观测的前向算法
def forward_continuous_hmm(pi, A, alpha, mu, sigma, obs):
    """连续观测HMM的前向算法"""
    T = len(obs)
    n_hidden = len(pi)
    n_gauss = alpha.shape[1]
    
    alpha_t = np.zeros((T, n_hidden))
    
    # 初始化
    for j in range(n_hidden):
        # 计算连续观测概率
        obs_prob = 0.0
        for k in range(n_gauss):
            obs_prob += alpha[j, k] * multivariate_normal.pdf(obs[0], mean=mu[j, k], cov=sigma[j, k])
        alpha_t[0, j] = pi[j] * obs_prob
    
    # 递推
    for t in range(1, T):
        for j in range(n_hidden):
            # 观测概率
            obs_prob = 0.0
            for k in range(n_gauss):
                obs_prob += alpha[j, k] * multivariate_normal.pdf(obs[t], mean=mu[j, k], cov=sigma[j, k])
            # 前向概率
            alpha_t[t, j] = np.sum(alpha_t[t-1] * A[:, j]) * obs_prob
    
    total_prob = np.sum(alpha_t[-1])
    return alpha_t, total_prob

# Viterbi算法（连续观测）
def viterbi_continuous_hmm(pi, A, alpha, mu, sigma, obs):
    """连续观测HMM的Viterbi算法"""
    T = len(obs)
    n_hidden = len(pi)
    n_gauss = alpha.shape[1]
    
    delta = np.zeros((T, n_hidden))
    psi = np.zeros((T, n_hidden), dtype=int)
    
    # 初始化
    for j in range(n_hidden):
        obs_prob = 0.0
        for k in range(n_gauss):
            obs_prob += alpha[j, k] * multivariate_normal.pdf(obs[0], mean=mu[j, k], cov=sigma[j, k])
        delta[0, j] = pi[j] * obs_prob
    
    # 递推
    for t in range(1, T):
        for j in range(n_hidden):
            obs_prob = 0.0
            for k in range(n_gauss):
                obs_prob += alpha[j, k] * multivariate_normal.pdf(obs[t], mean=mu[j, k], cov=sigma[j, k])
            temp = delta[t-1] * A[:, j]
            delta[t, j] = np.max(temp) * obs_prob
            psi[t, j] = np.argmax(temp)
    
    # 回溯
    best_seq = np.zeros(T, dtype=int)
    best_seq[-1] = np.argmax(delta[-1])
    for t in range(T-2, -1, -1):
        best_seq[t] = psi[t+1, best_seq[t+1]]
    
    return best_seq, delta

# 生成数据
np.random.seed(42)
hidden_seq, obs_seq = generate_continuous_hmm(pi, A, alpha, mu, sigma, seq_length=100)

# 执行Viterbi解码
best_seq, delta = viterbi_continuous_hmm(pi, A, alpha, mu, sigma, obs_seq)

# 可视化结果
fig = plt.figure(figsize=(14, 8))

# 子图1：观测序列（2维）
ax1 = fig.add_subplot(2, 2, 1)
ax1.scatter(obs_seq[:, 0], obs_seq[:, 1], c=hidden_seq, cmap='coolwarm', alpha=0.6, s=20)
ax1.set_xlabel('温度')
ax1.set_ylabel('湿度')
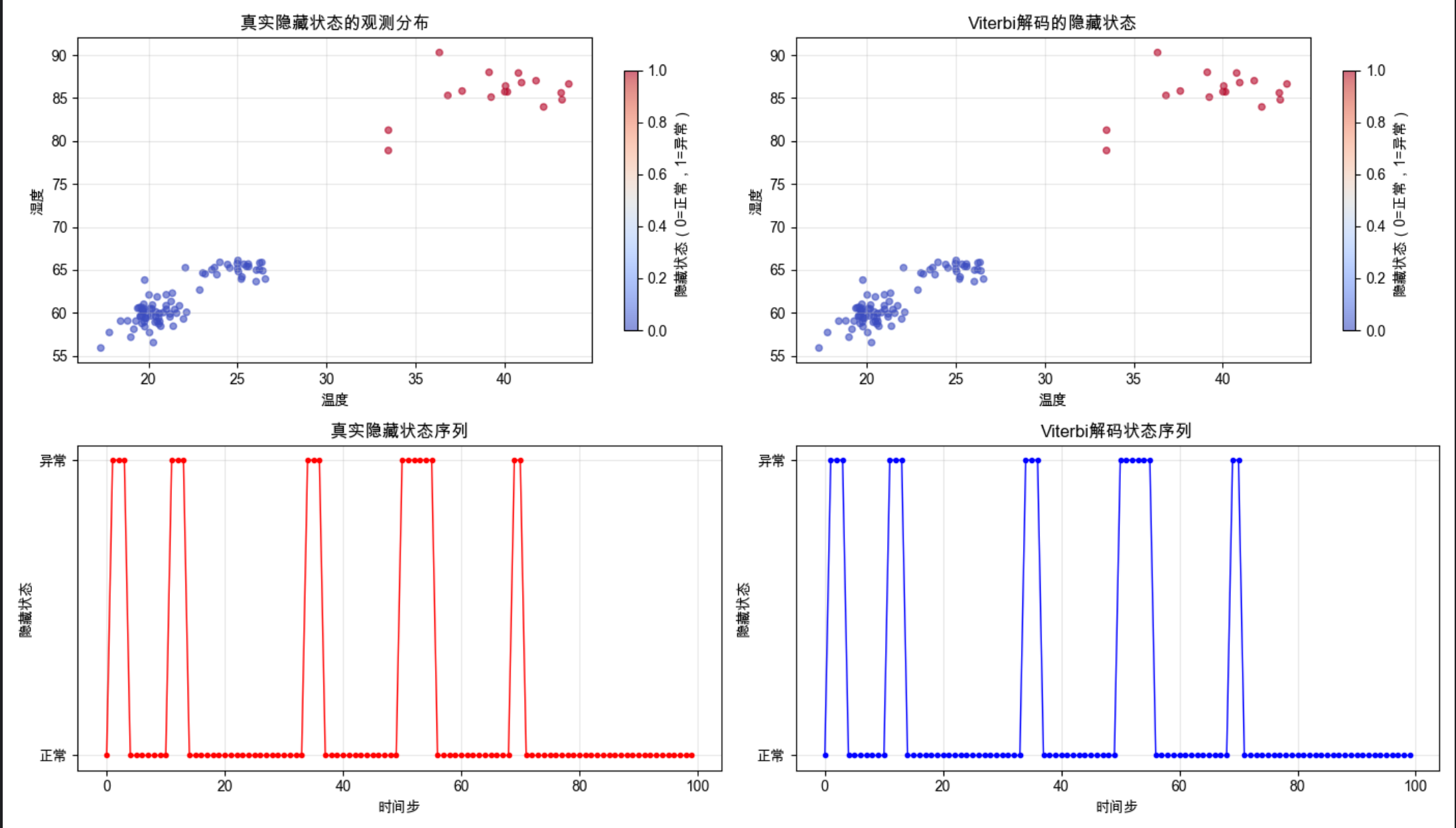
ax1.set_title('真实隐藏状态的观测分布')
ax1.grid(alpha=0.3)
cbar1 = plt.colorbar(ax1.collections[0], ax=ax1, shrink=0.8)
cbar1.set_label('隐藏状态（0=正常，1=异常）')

# 子图2：Viterbi解码结果
ax2 = fig.add_subplot(2, 2, 2)
ax2.scatter(obs_seq[:, 0], obs_seq[:, 1], c=best_seq, cmap='coolwarm', alpha=0.6, s=20)
ax2.set_xlabel('温度')
ax2.set_ylabel('湿度')
ax2.set_title('Viterbi解码的隐藏状态')
ax2.grid(alpha=0.3)
cbar2 = plt.colorbar(ax2.collections[0], ax=ax2, shrink=0.8)
cbar2.set_label('隐藏状态（0=正常，1=异常）')

# 子图3：真实状态序列
ax3 = fig.add_subplot(2, 2, 3)
ax3.plot(hidden_seq, marker='.', linewidth=1, color='red', label='真实状态')
ax3.set_xlabel('时间步')
ax3.set_ylabel('隐藏状态')
ax3.set_title('真实隐藏状态序列')
ax3.set_yticks([0, 1])
ax3.set_yticklabels(['正常', '异常'])
ax3.grid(alpha=0.3)

# 子图4：解码状态序列
ax4 = fig.add_subplot(2, 2, 4)
ax4.plot(best_seq, marker='.', linewidth=1, color='blue', label='解码状态')
ax4.set_xlabel('时间步')
ax4.set_ylabel('隐藏状态')
ax4.set_title('Viterbi解码状态序列')
ax4.set_yticks([0, 1])
ax4.set_yticklabels(['正常', '异常'])
ax4.grid(alpha=0.3)

plt.tight_layout()
plt.show()

# 计算解码准确率
accuracy = np.sum(best_seq == hidden_seq) / len(hidden_seq)
print(f"Viterbi解码准确率：{accuracy:.2%}")

15.9 HMM 作为图模型

HMM 可以用概率图模型表示，核心是 "有向图 + 马尔可夫性"：

HMM 概率图模型
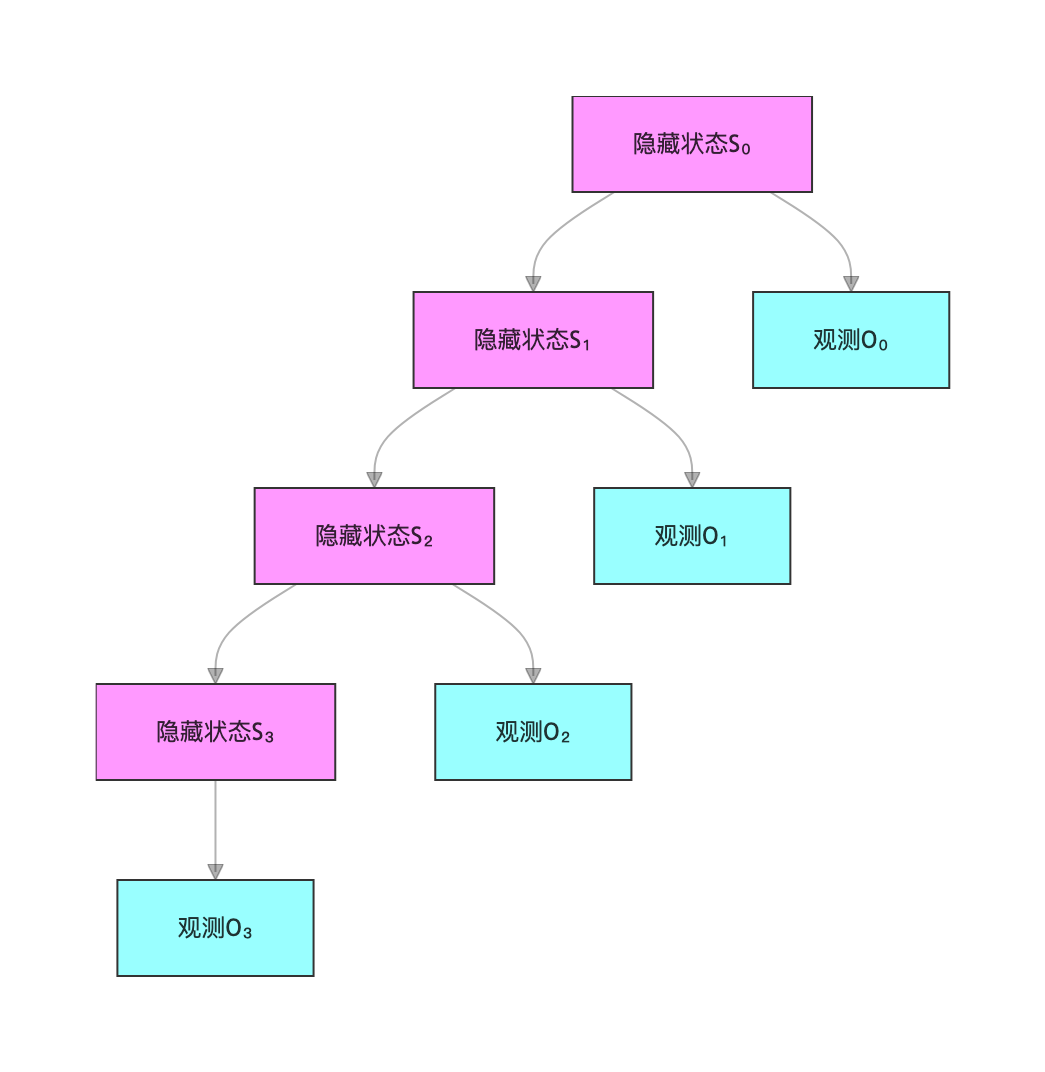
核心性质
  1. 马尔可夫性：P(St∣St−1,...,S0)=P(St∣St−1)
  2. 观测独立性：P(Ot∣St,St−1,Ot−1,...)=P(Ot∣St)
  3. 齐次性：状态转移概率不随时间变化

15.10 HMM 中的模型选择

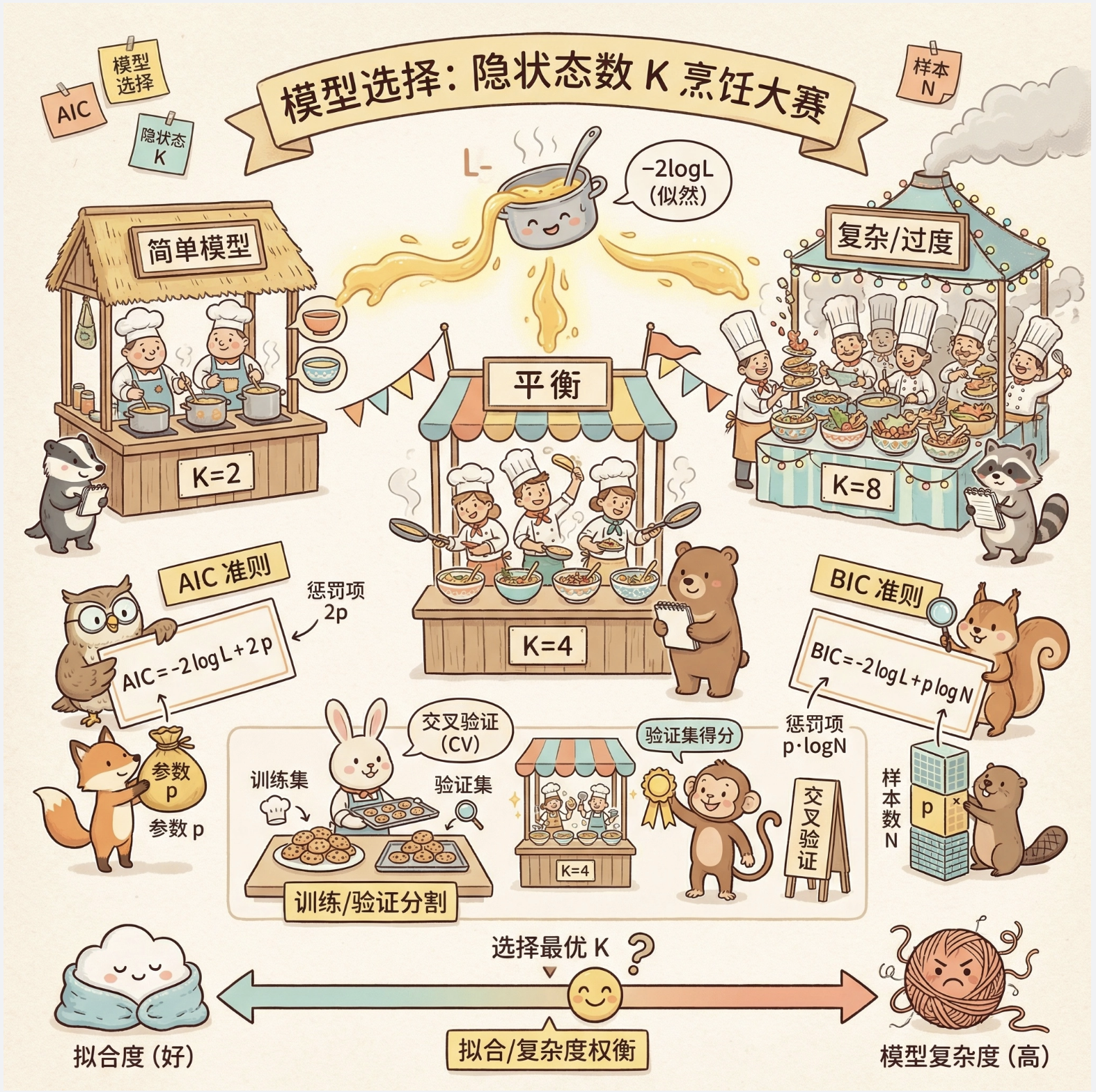
模型选择的核心是 "选择最优的隐藏状态数 K"，常用方法：

  1. AIC 准则：AIC=−2logL+2p（p 是参数个数）
  2. BIC 准则：BIC=−2logL+plogN（N 是样本数）
  3. 交叉验证：将数据分为训练集和验证集，选择验证集得分最高的 K
代码实战：HMM 模型选择（BIC 准则）
python 复制代码 
import numpy as np
import matplotlib.pyplot as plt

# 配置中文显示
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# ========== 补充缺失的核心函数：前向算法 ==========
def forward_algorithm(pi, A, B, obs):
    """
    前向算法计算观测序列的概率
    :param pi: 初始状态概率
    :param A: 状态转移矩阵
    :param B: 观测概率矩阵
    :param obs: 观测序列
    :return: 前向概率矩阵alpha，总概率P(O|λ)
    """
    T = len(obs)
    N = len(pi)
    alpha = np.zeros((T, N))
    
    # 初始化第一步
    alpha[0] = pi * B[:, obs[0]]
    
    # 递推计算后续步骤
    for t in range(1, T):
        for j in range(N):
            alpha[t, j] = np.sum(alpha[t-1] * A[:, j]) * B[j, obs[t]]
    
    # 总概率：最后一步所有状态的前向概率之和
    total_prob = np.sum(alpha[-1])
    return alpha, total_prob

# ========== 补充缺失的核心函数：后向算法 ==========
def backward_algorithm(pi, A, B, obs):
    """后向算法计算后向概率矩阵"""
    T = len(obs)
    N = len(pi)
    beta = np.zeros((T, N))

    # 初始化最后一步
    beta[-1] = 1.0

    # 递推
    for t in range(T - 2, -1, -1):
        for i in range(N):
            beta[t, i] = np.sum(A[i, :] * B[:, obs[t + 1]] * beta[t + 1, :])

    return beta

# ========== 补充缺失的核心函数：Baum-Welch算法 ==========
def baum_welch_algorithm(obs_sequences, n_hidden, n_obs, max_iter=100, tol=1e-6):
    """
    Baum-Welch算法估计HMM参数
    :param obs_sequences: 观测序列列表
    :param n_hidden: 隐藏状态数
    :param n_obs: 观测状态数
    :param max_iter: 最大迭代次数
    :param tol: 收敛阈值
    :return: 估计的pi, A, B，对数似然值序列
    """
    # 随机初始化参数（保证概率和为1）
    np.random.seed(42)
    pi = np.random.rand(n_hidden)
    pi = pi / np.sum(pi)

    A = np.random.rand(n_hidden, n_hidden)
    A = A / np.sum(A, axis=1, keepdims=True)

    B = np.random.rand(n_hidden, n_obs)
    B = B / np.sum(B, axis=1, keepdims=True)

    log_likelihoods = []

    for iter in range(max_iter):
        # 初始化累积变量
        pi_new = np.zeros(n_hidden)
        A_new = np.zeros_like(A)
        B_new = np.zeros_like(B)

        total_log_likelihood = 0.0

        for obs in obs_sequences:
            T = len(obs)
            # E步：计算前向、后向概率
            alpha, _ = forward_algorithm(pi, A, B, obs)
            beta = backward_algorithm(pi, A, B, obs)

            # 计算观测序列的对数似然
            log_likelihood = np.log(np.sum(alpha[-1]))
            total_log_likelihood += log_likelihood

            # 计算gamma（t时刻处于状态i的概率）
            gamma = alpha * beta
            gamma = gamma / np.sum(gamma, axis=1, keepdims=True)

            # 计算xi（t时刻处于i，t+1时刻处于j的概率）
            xi = np.zeros((T - 1, n_hidden, n_hidden))
            for t in range(T - 1):
                denominator = np.sum(alpha[t] @ A * B[:, obs[t + 1]] * beta[t + 1])
                for i in range(n_hidden):
                    xi[t, i, :] = alpha[t, i] * A[i, :] * B[:, obs[t + 1]] * beta[t + 1, :] / denominator

            # M步：累积统计量
            pi_new += gamma[0]
            A_new += np.sum(xi, axis=0)
            for j in range(n_hidden):
                for k in range(n_obs):
                    mask = (np.array(obs) == k)
                    B_new[j, k] += np.sum(gamma[mask, j])

        # 更新参数
        pi = pi_new / np.sum(pi_new)
        A = A_new / np.sum(A_new, axis=1, keepdims=True)
        B = B_new / np.sum(B_new, axis=1, keepdims=True)

        # 记录对数似然
        log_likelihoods.append(total_log_likelihood)

        # 检查收敛
        if iter > 0 and abs(log_likelihoods[-1] - log_likelihoods[-2]) < tol:
            print(f"K={n_hidden}时，算法在第{iter + 1}次迭代收敛")
            break

    return pi, A, B, log_likelihoods

# 生成模拟数据（3个隐藏状态）
true_pi = np.array([0.6, 0.3, 0.1])
true_A = np.array([[0.7, 0.2, 0.1], [0.3, 0.5, 0.2], [0.1, 0.3, 0.6]])
true_B = np.array([[0.8, 0.1, 0.1], [0.2, 0.6, 0.2], [0.1, 0.1, 0.8]])

# 生成观测序列
def generate_hmm_obs(pi, A, B, seq_length=100):
    N = len(pi)
    M = B.shape[1]
    hidden_seq = [np.random.choice(N, p=pi)]
    for _ in range(1, seq_length):
        hidden_seq.append(np.random.choice(N, p=A[hidden_seq[-1]]))
    obs_seq = [np.random.choice(M, p=B[s]) for s in hidden_seq]
    return obs_seq

# 生成10个观测序列
np.random.seed(42)
obs_sequences = [generate_hmm_obs(true_pi, true_A, true_B, 100) for _ in range(10)]

# 计算不同K的BIC
def calculate_bic(log_likelihood, n_params, n_samples):
    """计算BIC值"""
    return -2 * log_likelihood + n_params * np.log(n_samples)

# 尝试不同的隐藏状态数K（1-5）
K_candidates = [1, 2, 3, 4, 5]
bic_scores = []
log_likelihoods = []

for K in K_candidates:
    # 用Baum-Welch估计模型
    pi_est, A_est, B_est, ll_list = baum_welch_algorithm(
        obs_sequences, n_hidden=K, n_obs=3, max_iter=30, tol=1e-4
    )

    # 计算总对数似然
    total_ll = ll_list[-1]
    log_likelihoods.append(total_ll)

    # 计算参数个数：pi(K) + A(K²) + B(K*M)
    n_params = K + K * K + K * 3
    # 总样本数
    n_samples = len(obs_sequences) * len(obs_sequences[0])
    # 计算BIC
    bic = calculate_bic(total_ll, n_params, n_samples)
    bic_scores.append(bic)

# 可视化模型选择结果
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))

# 子图1：对数似然 vs K
ax1.plot(K_candidates, log_likelihoods, marker='o', linewidth=2, color='blue')
ax1.set_xlabel('隐藏状态数K')
ax1.set_ylabel('总对数似然值')
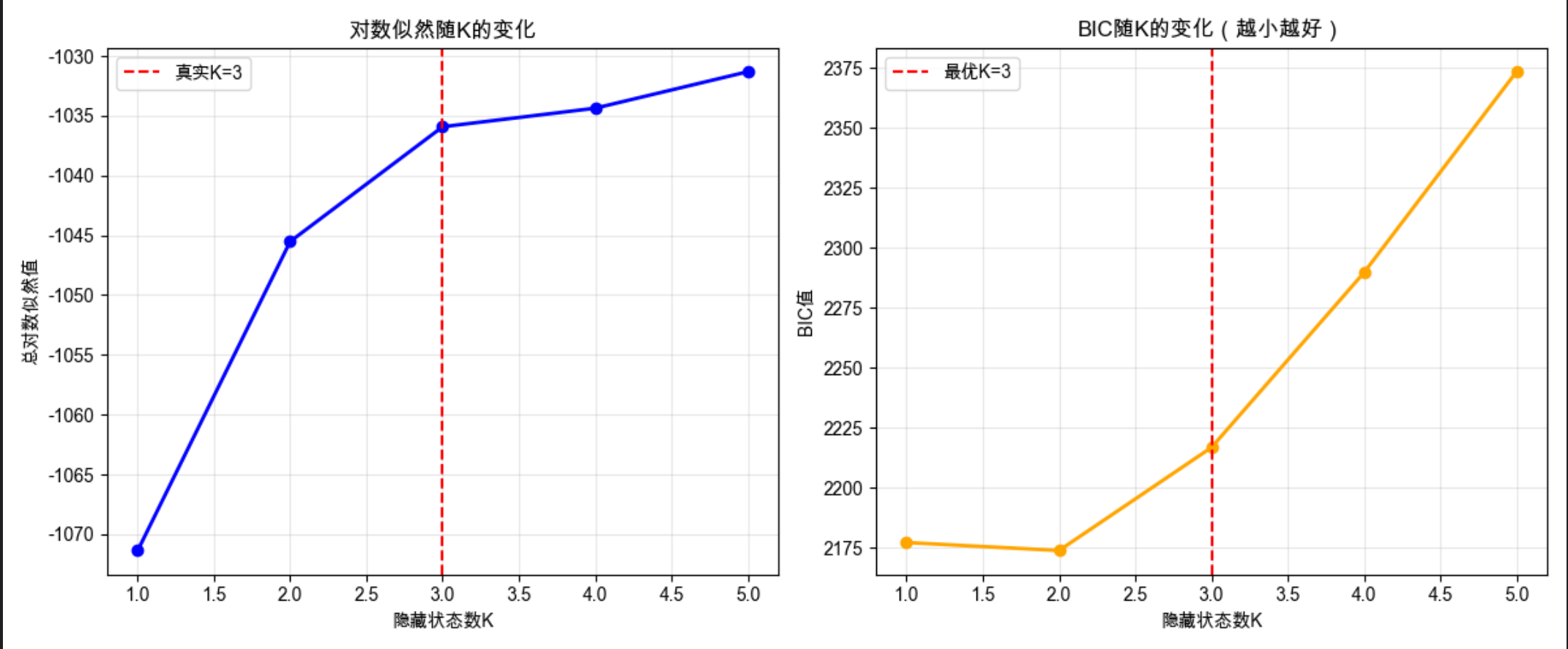
ax1.set_title('对数似然随K的变化')
ax1.grid(alpha=0.3)
ax1.axvline(x=3, color='red', linestyle='--', label='真实K=3')
ax1.legend()

# 子图2：BIC vs K
ax2.plot(K_candidates, bic_scores, marker='o', linewidth=2, color='orange')
ax2.set_xlabel('隐藏状态数K')
ax2.set_ylabel('BIC值')
ax2.set_title('BIC随K的变化（越小越好）')
ax2.grid(alpha=0.3)
ax2.axvline(x=3, color='red', linestyle='--', label='最优K=3')
ax2.legend()

plt.tight_layout()
plt.show()

# 输出结果
print("=== 模型选择结果 ===")
for K, bic, ll in zip(K_candidates, bic_scores, log_likelihoods):
    print(f"K={K}: BIC={bic:.2f}, 对数似然={ll:.2f}")

best_K = K_candidates[np.argmin(bic_scores)]
print(f"\n根据BIC准则，最优隐藏状态数为：K={best_K}")

15.11 注释

  1. HMM 由 L.E. Baum 等人在 1966 年提出，最初用于语音识别
  2. Baum-Welch 算法是 EM 算法的特例，只能保证收敛到局部最优
  3. Viterbi 算法不仅用于 HMM 解码，还广泛应用于通信、生物信息学等领域
  4. 连续观测 HMM 常被称为 GHMM（Gaussian HMM），是语音识别的核心模型

15.12 习题

  1. 手动计算：给定 HMM 参数和短观测序列，用前向算法计算观测概率
  2. 编程题：修改 Viterbi 算法，输出前 3 个最可能的状态序列
  3. 应用题：用 HMM 实现中文分词（隐藏状态：B/M/E/S，观测：汉字）
  4. 思考题：对比 HMM 和 CRF 在序列标注任务中的优缺点

15.13 参考文献

  1. 《机器学习》- 周志华
  2. 《统计学习方法》- 李航
  3. Rabiner L R. A tutorial on hidden Markov models and selected applications in speech recognition[J]. Proceedings of the IEEE, 1989
  4. Baum L E, Petrie T, Soules G, et al. A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains[J]. The annals of mathematical statistics, 1970

总结

1.HMM 核心 ：由隐藏马尔可夫链（状态转移）和观测模型（观测概率）组成，解决估值、解码、学习三大问题。

2.核心算法 ：前向 / 后向算法（估值）、Viterbi 算法（解码）、Baum-Welch 算法（参数学习），均基于动态规划思想，避免暴力枚举的高复杂度。

3.实战要点 ：离散观测 HMM 适用于分类观测，连续观测 HMM（高斯混合）适用于数值观测；模型选择可通过AIC/BIC 准则确定最优隐藏状态数。

希望这篇文章能帮你彻底搞懂 HMM！所有代码都可直接运行，建议大家动手跑一遍，加深理解。如果有问题，欢迎在评论区交流～

相关推荐
九.九8 小时前
ops-transformer：AI 处理器上的高性能 Transformer 算子库
人工智能·深度学习·transformer
春日见8 小时前
拉取与合并：如何让个人分支既包含你昨天的修改，也包含 develop 最新更新
大数据·人工智能·深度学习·elasticsearch·搜索引擎
恋猫de小郭8 小时前
AI 在提高你工作效率的同时，也一直在增加你的疲惫和焦虑
前端·人工智能·ai编程
寻寻觅觅☆8 小时前
东华OJ-基础题-106-大整数相加（C++）
开发语言·c++·算法
YJlio8 小时前
1.7 通过 Sysinternals Live 在线运行工具：不下载也能用的“云端工具箱”
c语言·网络·python·数码相机·ios·django·iphone
deephub8 小时前
Agent Lightning：微软开源的框架无关 Agent 训练方案，LangChain/AutoGen 都能用
人工智能·microsoft·langchain·大语言模型·agent·强化学习
偷吃的耗子9 小时前
【CNN算法理解】：三、AlexNet 训练模块(附代码)
深度学习·算法·cnn
l1t9 小时前
在wsl的python 3.14.3容器中使用databend包
开发语言·数据库·python·databend
大模型RAG和Agent技术实践9 小时前
从零构建本地AI合同审查系统：架构设计与流式交互实战（完整源代码）
人工智能·交互·智能合同审核
老邋遢9 小时前
第三章-AI知识扫盲看这一篇就够了
人工智能
热门推荐
01GitHub 镜像站点02Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services03openclaw配置教程（linux+局域网ollama）04UV安装并设置国内源05Linux下V2Ray安装配置指南06openclaw使用nginx反代部署过程 与disconnected (1008): pairing required解决07AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南08【Linux操作系统12】Git版本控制与GDB调试：从入门到实践09简单模板笔记10基于MATLAB的Copula对数似然值计算与参数验证