200. 岛屿数量
深搜版本:
python
class Solution(object):
def dfs(self, grid, x, y, n, m):
grid[x][y] = '0'
for i,j in [[x+1,y],[x-1,y],[x,y+1],[x,y-1]]:
if 0<=i<n and 0<=j<m and grid[i][j] == '1':
self.dfs(grid,i,j,n,m)
def numIslands(self, grid):
"""
:type grid: List[List[str]]
:rtype: int
"""
# 本质是找连通分量的数量
# 题目没说是否可以修改原数组,我们默认可以修改
# 注意,如果不能修改,那么需要使用visited数据进行访问节点的标记
# 这里,为了节省空间,直接修改原图
n = len(grid)
if n == 0:
return 0
m = len(grid[0])
res = 0
for i in range(n):
for j in range(m):
if grid[i][j] == '1':
res +=1
self.dfs(grid,i,j, n, m)
return res时间复杂度:O(MN) # 每个节点过一遍
空间复杂度:O(MN) # 最坏情况:全是陆地,栈全存一遍
广搜版本:
python
class Solution(object):
def numIslands(self, grid):
"""
:type grid: List[List[str]]
:rtype: int
"""
n = len(grid)
if n == 0:
return 0
m = len(grid[0])
res = 0
for i in range(n):
for j in range(m):
if grid[i][j] == '1':
res +=1
# 广搜用队列
grid[i][j] = '0'
queue = [(i,j)]
while queue:
x,y = queue.pop(0)
for u,v in [[x+1,y],[x-1,y],[x,y+1],[x,y-1]]:
if 0<=u<n and 0<=v<m and grid[u][v] == '1':
grid[u][v] = '0'
queue.append((u,v))
return res时间复杂度:O(MN) # 每个节点过一遍
空间复杂度:O(min(M,N)) # 最坏情况:全是陆地,队列最大就是存一行或一列
994. 腐烂的橘子
python
class Solution(object):
def orangesRotting(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
# 多源广度优先搜索
n,m = len(grid), len(grid[0]) # 题目明确m,n 均>1
queue = collections.deque()
for i in range(n):
for j in range(m):
if grid[i][j] == 2:
queue.append((i,j,0)) # 需要存一下时间
t = 0
while queue:
x,y,t = queue.popleft()
for i,j in [[x+1,y],[x-1,y],[x,y+1],[x,y-1]]:
if 0<=i<n and 0<=j<m and grid[i][j] == 1:
grid[i][j] = 2
queue.append((i,j,t+1))
# 如果循环结束,说明最后一个t就是res
# 如果不连通 可能有一些橘子永远无法腐烂
if any(1 in row for row in grid):
return -1
return t时间复杂度:O(nm)
空间复杂度:O(nm) # 最差是O(nm)
207. 课程表
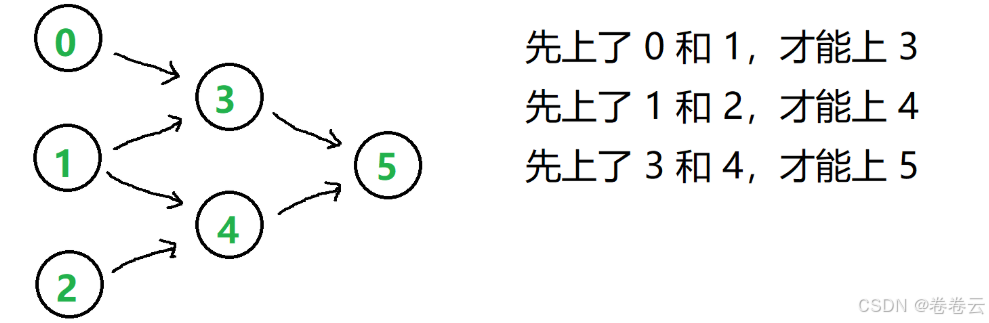
有向无环图 -> 线性拓扑排序 【我们要证明有向图无环!】
深搜版本:
构建图:[a,b] 修完b才能修a,所以b->a
对于图中的任意一个节点,在搜索的过程中有三种状态:
- 未搜索:还没有搜索到这个节点;
- 搜索中:搜索过这个节点,但还没有回溯到该节点,即该节点还没有入栈,还有相邻的节点没有搜索完成);一旦搜索中发现这样的节点,就意味着沿着该节点出发回到了该节点,出现了环。
- 已完成:我们搜索过并且回溯过这个节点,即该节点已经入栈,该节点没有环,此时新入的节点的先后不会居于该节点之后。
在每一轮的搜索搜索开始时,任取一个「未搜索」的节点开始进行DFS。将当前搜索的节点 u 标记为「搜索中」,遍历该节点的每一个相邻节点 v:
- 如果 v 为「未搜索」,搜索 v,待搜索完成回溯到 u;
- 如果 v 为「搜索中」,就找到了图中的一个环;
- 如果 v 为「已完成」,那么说明 v 已经在栈中了,而 u 还不在栈中,要么是先修u,v在u之后,要么是二者顺序无关。
当 u 的所有相邻节点都为「已完成」时,将 u 放入栈中,并将其标记为「已完成」。
python
class Solution(object):
def canFinish(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: bool
"""
# visited数组:0 未搜索 1 搜索中 2 已完成
visited = [0 for _ in range(numCourses)]
edges = collections.defaultdict(list)
self.res = True
# 这里如果只是想判断是否有环,不需要栈来存储
# 把已完成的节点压入栈中,然后从栈顶到栈底,其实就是一条可行的链式拓扑结构
st = []
# 邻接表存图
for u,v in prerequisites:
edges[v].append(u)
def dfs(u):
visited[u] = 1
for v in edges[u]:
if not visited[v]:
dfs(v)
if not self.res:
return
elif visited[v] == 1:
# 出现了环
self.res = False
return
visited[u] = 2
st.append(u)
for i in range(numCourses):
if self.res and not visited[i]:
dfs(i) # 有可能是非连通图
return self.res时间复杂度:O(n+m) # n是课程数,m是先修课程数
空间复杂度:O(n+m)
广搜版本:
广搜版本更加符合拓扑排序的直觉。
使用一个队列来进行广搜。初始时,所有入度为 0 的节点都被放入队列中,作为拓扑排序最前面的节点,并且它们之间的相对顺序无关紧要。
在广度优先搜索的每一步中,取出队首的节点 u,将 u 的所有相邻节点的入度减少 1【移除下一个节点的入边】。如果某个相邻节点 v 的入度变为 0,那么就将 v 放入队列中。
在广度优先搜索的过程结束后。如果答案中包含了这 n 个节点,那么就找到了一种拓扑排序,否则说明图中存在环。
python
class Solution(object):
def canFinish(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: bool
"""
edges = collections.defaultdict(list)
indge = [0 for _ in range(numCourses)]
res = []
# 如果只是想得到是否无环,仅仅计数看过的节点个数;但是如果想得到拓扑排序,需要用数组记录
for u,v in prerequisites:
edges[v].append(u)
indge[u] +=1
queue = collections.deque([u for u in range(numCourses) if indge[u]==0])
while queue:
u = queue.popleft()
res.append(u)
for v in edges[u]:
indge[v] -=1
if indge[v] ==0:
queue.append(v)
return len(res) == numCourses时间复杂度:O(n+m) # n是课程数,m是先修课程数
空间复杂度:O(n+m)
208. 前缀树
208. 实现 Trie (前缀树) - 力扣(LeetCode)
python
class Trie(object):
def __init__(self):
self.children = [None]*26
self.isEnd = False
def insert(self, word):
node = self # 真的好好品!
for c in word:
ch = ord(c) - ord('a')
if not node.children[ch]:
node.children[ch] = Trie()
node = node.children[ch]
node.isEnd = True
def _searchPrefix(self, prefix):
node = self
for c in prefix:
ch = ord(c) - ord('a')
if not node.children[ch]:
return None
node = node.children[ch]
return node
def search(self, word):
return self._searchPrefix(word) is not None and self._searchPrefix(word).isEnd
def startsWith(self, prefix):
return self._searchPrefix(prefix) is not None时间复杂度:初始化为 O(1),其余操作为 O(n),n是每次插入或查询的word的长度。
空间复杂度:O(T⋅Σ),其中 T为所有已经插入字符串的长度之和,Σ 为字符集的大小,这里是26。