【LeetCode】116. 填充每个节点的下一个右侧节点指针

熬了夜的程序员2026-02-13 8:39

116. 填充每个节点的下一个右侧节点指针

文章目录

题目描述

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

C++ 复制代码 
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例 1：

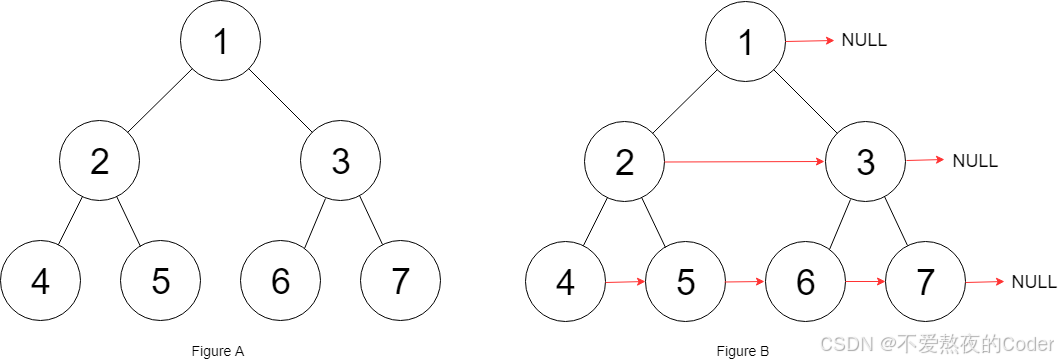
输入 ：root = [1,2,3,4,5,6,7]

输出 ：[1,#,2,3,#,4,5,6,7,#]

解释 ：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

示例 2：

输入 ：root = []

输出 ：[]

提示：

  • 树中节点的数量在 [0, 2^12 - 1] 范围内
  • -1000 <= node.val <= 1000

进阶：

  • 你只能使用常量级额外空间。
  • 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

问题深度分析

这是一道二叉树层序遍历的变种问题 ，核心在于利用已建立的 next 指针进行空间优化 。题目要求填充每个节点的 next 指针，使其指向同一层的下一个右侧节点。对于完美二叉树，我们可以利用其结构特性（每层节点数确定、左右子树对称）来实现高效的算法。

问题本质

给定一个完美二叉树，需要为每个节点建立指向同一层右侧相邻节点 的 next 指针。关键点：

  • 同一层：节点必须在同一深度
  • 右侧相邻：必须是紧邻的右侧节点
  • 完美二叉树：所有叶子节点在同一层，每个节点都有两个子节点

核心思想

利用已建立的 next 指针：

  1. 层序遍历思路 ：逐层处理，为每层节点建立 next 连接
  2. 递归思路 ：利用父节点的 next 指针连接跨子树的节点
  3. 迭代优化 ：利用已建立的 next 指针，实现 O(1) 空间复杂度

关键难点

  1. 跨子树连接：左子树的右节点需要连接到右子树的左节点
  2. 空间优化：如何在 O(1) 空间内完成操作
  3. 边界处理 ：每层最后一个节点的 next 应为 NULL

算法对比

方法 时间复杂度 空间复杂度 特点
方法一：层序遍历（BFS） O(n) O(w) 直观易懂，需要队列存储
方法二：递归连接 O(n) O(h) 利用递归栈，代码简洁
方法三：迭代 O(1) 空间 O(n) O(1) 最优解，利用 next 指针
方法四：DFS 前序遍历 O(n) O(h) 深度优先，先处理父节点

说明：

  • n：节点总数
  • w：树的最大宽度（最后一层节点数）
  • h：树的高度

算法流程图

主算法流程

是
否
是
否
是
否
开始
根节点是否为空?
返回空
选择算法方法
方法一: BFS层序遍历
方法二: 递归连接
方法三: 迭代O1空间
方法四: DFS前序遍历
创建队列
逐层处理节点
连接同层相邻节点
处理下一层
是否还有层?
完成
递归处理左右子树
连接同一父节点的子节点
利用父节点next连接跨子树节点
递归处理子节点
从根节点开始
逐层处理
利用已建立的next指针遍历
连接下一层节点
是否还有层?
前序遍历当前节点
连接当前节点的子节点
递归处理左子树
递归处理右子树
结束

方法三：迭代 O(1) 空间详细流程

是
否
是
否
是
否
开始: root节点
初始化: leftmost = root
leftmost是否为空?
结束
当前节点curr = leftmost
curr是否为空?
更新leftmost到下一层
连接curr.left.next = curr.right
curr.next是否存在?
连接curr.right.next = curr.next.left
curr.right.next = NULL
curr = curr.next
返回root

跨子树连接示意图

子节点层
父节点层
next
next
next
next
建立连接
建立连接
通过A.next建立
Node A
Node B
A.left
A.right
B.left
B.right

复杂度分析

时间复杂度

所有方法均为 O(n)：

  • 每个节点被访问一次
  • 每个节点的 next 指针被设置一次
  • 总操作次数与节点数成正比

空间复杂度

  1. 方法一（BFS）：O(w)

    • 队列最多存储一层的节点
    • 完美二叉树最后一层有 2^(h-1) 个节点
    • w = 2^(h-1) = O(n/2) = O(n)

  2. 方法二（递归）：O(h)

    • 递归调用栈深度等于树的高度
    • 完美二叉树高度 h = log₂(n+1)
    • O(log n)

  3. 方法三（迭代 O(1)）：O(1)

    • 只使用常数额外变量
    • 利用已建立的 next 指针遍历

  4. 方法四（DFS）：O(h)

    • 递归调用栈深度等于树的高度
    • O(log n)

关键优化技巧

技巧一：利用 next 指针实现 O(1) 空间

核心思想 ：已建立的 next 指针可以作为"横向链表"，用于遍历当前层，从而建立下一层的连接。

go 复制代码 
// 方法三：迭代 O(1) 空间
func connect3(root *Node) *Node {
    if root == nil {
        return nil
    }
    
    leftmost := root
    for leftmost.Left != nil {  // 还有下一层
        curr := leftmost
        for curr != nil {
            // 连接同一父节点的子节点
            curr.Left.Next = curr.Right
            
            // 连接跨子树的节点
            if curr.Next != nil {
                curr.Right.Next = curr.Next.Left
            }
            
            curr = curr.Next  // 利用next指针横向移动
        }
        leftmost = leftmost.Left  // 移动到下一层
    }
    
    return root
}

优势：

  • 空间复杂度 O(1)
  • 时间复杂度 O(n)
  • 完美利用完美二叉树的结构特性

技巧二：递归连接跨子树节点

核心思想 ：利用父节点的 next 指针，连接不同父节点的子节点。

go 复制代码 
// 方法二：递归连接
func connect2(root *Node) *Node {
    if root == nil {
        return nil
    }
    
    // 连接同一父节点的子节点
    if root.Left != nil {
        root.Left.Next = root.Right
    }
    
    // 利用父节点的next连接跨子树的节点
    if root.Right != nil && root.Next != nil {
        root.Right.Next = root.Next.Left
    }
    
    // 递归处理左右子树
    connect2(root.Left)
    connect2(root.Right)
    
    return root
}

优势：

  • 代码简洁清晰
  • 逻辑直观易懂
  • 空间复杂度 O(log n)

技巧三：BFS 层序遍历

核心思想 ：使用队列逐层处理，为每层节点建立 next 连接。

go 复制代码 
// 方法一：BFS层序遍历
func connect1(root *Node) *Node {
    if root == nil {
        return nil
    }
    
    queue := []*Node{root}
    for len(queue) > 0 {
        size := len(queue)
        for i := 0; i < size; i++ {
            node := queue[0]
            queue = queue[1:]
            
            // 连接同层相邻节点
            if i < size-1 {
                node.Next = queue[0]
            }
            
            // 添加子节点到队列
            if node.Left != nil {
                queue = append(queue, node.Left)
            }
            if node.Right != nil {
                queue = append(queue, node.Right)
            }
        }
    }
    
    return root
}

优势：

  • 思路直观
  • 适用于任意二叉树
  • 易于理解和实现

技巧四：DFS 前序遍历

核心思想：先处理父节点建立连接，再递归处理子节点。

go 复制代码 
// 方法四：DFS前序遍历
func connect4(root *Node) *Node {
    if root == nil {
        return nil
    }
    
    // 连接当前节点的子节点
    if root.Left != nil {
        root.Left.Next = root.Right
        if root.Next != nil {
            root.Right.Next = root.Next.Left
        }
    }
    
    // 递归处理左右子树
    connect4(root.Left)
    connect4(root.Right)
    
    return root
}

优势：

  • 深度优先遍历
  • 先处理父节点，再处理子节点
  • 逻辑清晰

边界情况处理

1. 空树

go 复制代码 
if root == nil {
    return nil
}

2. 单节点树

  • 根节点的 next 保持为 NULL
  • 无需特殊处理

3. 每层最后一个节点

  • 最后一个节点的 next 应为 NULL
  • BFS 方法中通过索引判断：if i < size-1

4. 叶子节点层

  • 叶子节点没有子节点
  • 迭代方法中通过 leftmost.Left != nil 判断是否还有下一层

测试用例设计

基础测试

  1. 空树

    • 输入：[]
    • 输出：[]

  2. 单节点

    • 输入：[1]
    • 输出：[1,#]

  3. 两层树

    • 输入：[1,2,3]
    • 输出：[1,#,2,3,#]
    • 验证：节点2的next指向节点3

标准测试

  1. 三层完美二叉树

    • 输入：[1,2,3,4,5,6,7]
    • 输出：[1,#,2,3,#,4,5,6,7,#]
    • 验证：
      • 节点2的next指向节点3
      • 节点4的next指向节点5
      • 节点5的next指向节点6
      • 节点6的next指向节点7

  2. 四层完美二叉树

    • 输入：[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]
    • 验证：每层节点正确连接

边界测试

  1. 最大深度树

    • 测试递归深度限制
    • 验证空间复杂度

  2. 单侧树（非完美二叉树，用于测试）

    • 注意：完美二叉树不会有这种情况
    • 但可以测试算法的健壮性

常见错误与陷阱

错误一：忘记处理跨子树连接

错误代码：

go 复制代码 
// 只连接了同一父节点的子节点
curr.Left.Next = curr.Right
// 忘记了跨子树的连接！

正确做法：

go 复制代码 
curr.Left.Next = curr.Right
if curr.Next != nil {
    curr.Right.Next = curr.Next.Left  // 跨子树连接
}

错误二：在建立连接前访问 next

错误代码：

go 复制代码 
// 错误：在建立连接前就使用next指针
for curr != nil {
    curr = curr.Next  // 此时next可能还未建立
    curr.Left.Next = curr.Right
}

正确做法：

go 复制代码 
// 先建立连接，再移动
for curr != nil {
    curr.Left.Next = curr.Right
    if curr.Next != nil {
        curr.Right.Next = curr.Next.Left
    }
    curr = curr.Next  // 建立连接后再移动
}

错误三：BFS 中队列大小变化

错误代码：

go 复制代码 
for len(queue) > 0 {
    node := queue[0]
    queue = queue[1:]
    // 错误：队列大小在循环中变化
    if len(queue) > 0 {
        node.Next = queue[0]
    }
    // ...
}

正确做法：

go 复制代码 
for len(queue) > 0 {
    size := len(queue)  // 固定当前层大小
    for i := 0; i < size; i++ {
        node := queue[0]
        queue = queue[1:]
        if i < size-1 {  // 使用索引判断
            node.Next = queue[0]
        }
        // ...
    }
}

实战技巧总结

1. 完美二叉树特性利用

  • 结构对称：左右子树结构完全相同
  • 层数确定：所有叶子节点在同一层
  • 节点数确定 ：第 i 层有 2^(i-1) 个节点

2. next 指针的双重作用

  • 结果：存储答案（指向右侧节点）
  • 工具：用于遍历当前层（在迭代方法中）

3. 空间优化思路

  • 利用已有结构 ：使用 next 指针代替队列
  • 逐层处理：处理完一层再处理下一层
  • 避免存储：不存储所有节点，只存储必要信息

4. 递归 vs 迭代

  • 递归：代码简洁，但空间复杂度 O(log n)
  • 迭代：空间复杂度 O(1)，但代码稍复杂
  • 选择：根据题目要求选择合适方法

进阶扩展

扩展一：非完美二叉树（LeetCode 117）

  • 节点可能缺失
  • 需要处理 nil 节点
  • 需要找到每层第一个非空节点

扩展二：N 叉树

  • 每个节点有多个子节点
  • 需要连接所有相邻的子节点
  • 算法需要相应调整

扩展三：从任意节点开始

  • 给定树中某个节点
  • 填充该节点所在层的所有 next 指针
  • 需要先找到该层的起始节点

扩展四：双向链表

  • 不仅建立向右的 next 指针
  • 还建立向左的 prev 指针
  • 形成双向链表结构

应用场景

1. 树形结构的横向遍历

  • 场景：需要按层遍历树，但不想使用队列
  • 优势 ：利用 next 指针可以直接遍历同一层

2. 完美二叉树的特殊操作

  • 场景：对完美二叉树进行层序相关操作
  • 优势：可以利用结构特性优化算法

3. 空间受限环境

  • 场景：内存有限，需要 O(1) 空间算法
  • 优势：迭代方法满足空间要求

4. 树形数据结构的序列化

  • 场景：需要按层序列化树结构
  • 优势 ：next 指针提供了层序信息

相关题目

  • 117. 填充每个节点的下一个右侧节点指针 II：非完美二叉树版本
  • 102. 二叉树的层序遍历：层序遍历基础
  • 103. 二叉树的锯齿形层序遍历：层序遍历变种
  • 199. 二叉树的右视图：利用层序遍历

总结

本题是二叉树层序遍历的经典变种 ，核心在于利用已建立的 next 指针实现空间优化。通过四种不同的方法，我们展示了：

  1. BFS 方法：直观易懂，适用于理解问题
  2. 递归方法：代码简洁，逻辑清晰
  3. 迭代 O(1) 方法：最优解，空间效率最高
  4. DFS 方法：深度优先，先处理父节点

关键要点：

  • 完美二叉树的结构特性可以用于优化
  • next 指针既可以存储结果，也可以作为遍历工具
  • 跨子树连接是本题的核心难点
  • 空间优化需要充分利用已有结构

掌握本题有助于理解树形结构的层序遍历 和空间优化技巧，为后续更复杂的树形问题打下基础。

完整题解代码

go 复制代码 
package main

import (
	"fmt"
)

// =========================== Node 定义 ===========================
type Node struct {
	Val   int
	Left  *Node
	Right *Node
	Next  *Node
}

// =========================== 方法一：BFS层序遍历 ===========================
// 时间复杂度：O(n)，空间复杂度：O(w)，w为树的最大宽度
func connect1(root *Node) *Node {
	if root == nil {
		return nil
	}

	queue := []*Node{root}
	for len(queue) > 0 {
		size := len(queue)
		for i := 0; i < size; i++ {
			node := queue[0]
			queue = queue[1:]

			// 连接同层相邻节点（不是最后一个节点）
			if i < size-1 {
				node.Next = queue[0]
			}

			// 添加子节点到队列
			if node.Left != nil {
				queue = append(queue, node.Left)
			}
			if node.Right != nil {
				queue = append(queue, node.Right)
			}
		}
	}

	return root
}

// =========================== 方法二：递归连接 ===========================
// 时间复杂度：O(n)，空间复杂度：O(h)，h为树的高度
func connect2(root *Node) *Node {
	if root == nil {
		return nil
	}

	// 连接同一父节点的子节点
	if root.Left != nil {
		root.Left.Next = root.Right
	}

	// 利用父节点的next连接跨子树的节点
	if root.Right != nil && root.Next != nil {
		root.Right.Next = root.Next.Left
	}

	// 递归处理左右子树
	connect2(root.Left)
	connect2(root.Right)

	return root
}

// =========================== 方法三：迭代 O(1) 空间（最优解） ===========================
// 时间复杂度：O(n)，空间复杂度：O(1)
func connect3(root *Node) *Node {
	if root == nil {
		return nil
	}

	// leftmost指向每层最左边的节点
	leftmost := root

	// 逐层处理，直到叶子节点层
	for leftmost.Left != nil {
		// 当前层的当前节点
		curr := leftmost

		// 遍历当前层的所有节点
		for curr != nil {
			// 连接同一父节点的子节点
			curr.Left.Next = curr.Right

			// 连接跨子树的节点
			if curr.Next != nil {
				curr.Right.Next = curr.Next.Left
			}

			// 移动到当前层的下一个节点
			curr = curr.Next
		}

		// 移动到下一层
		leftmost = leftmost.Left
	}

	return root
}

// =========================== 方法四：DFS前序遍历 ===========================
// 时间复杂度：O(n)，空间复杂度：O(h)，h为树的高度
func connect4(root *Node) *Node {
	if root == nil {
		return nil
	}

	// 连接当前节点的子节点
	if root.Left != nil {
		root.Left.Next = root.Right
		// 如果当前节点有next，连接跨子树的节点
		if root.Next != nil {
			root.Right.Next = root.Next.Left
		}
	}

	// 递归处理左右子树
	connect4(root.Left)
	connect4(root.Right)

	return root
}

// =========================== 工具函数：从数组构建完美二叉树 ===========================
func arrayToTreeLevelOrder(arr []interface{}) *Node {
	if len(arr) == 0 || arr[0] == nil {
		return nil
	}

	root := &Node{Val: arr[0].(int)}
	queue := []*Node{root}
	i := 1

	for i < len(arr) && len(queue) > 0 {
		node := queue[0]
		queue = queue[1:]

		// 左子节点
		if i < len(arr) && arr[i] != nil {
			left := &Node{Val: arr[i].(int)}
			node.Left = left
			queue = append(queue, left)
		}
		i++

		// 右子节点
		if i < len(arr) && arr[i] != nil {
			right := &Node{Val: arr[i].(int)}
			node.Right = right
			queue = append(queue, right)
		}
		i++
	}

	return root
}

// =========================== 工具函数：验证next指针连接 ===========================
func validateNextPointers(root *Node) []string {
	if root == nil {
		return []string{}
	}

	var result []string
	leftmost := root

	// 逐层遍历
	for leftmost != nil {
		curr := leftmost
		level := []int{}

		// 通过next指针遍历当前层
		for curr != nil {
			level = append(level, curr.Val)
			curr = curr.Next
		}

		// 格式化输出
		levelStr := ""
		for i, v := range level {
			if i > 0 {
				levelStr += " -> "
			}
			levelStr += fmt.Sprintf("%d", v)
		}
		result = append(result, levelStr)

		// 移动到下一层
		leftmost = leftmost.Left
	}

	return result
}

// =========================== 工具函数：按层序输出（带next信息） ===========================
func levelOrderWithNext(root *Node) []interface{} {
	if root == nil {
		return []interface{}{}
	}

	var result []interface{}
	leftmost := root

	for leftmost != nil {
		curr := leftmost
		for curr != nil {
			result = append(result, curr.Val)
			curr = curr.Next
		}
		result = append(result, "#") // 层分隔符
		leftmost = leftmost.Left
	}

	return result
}

// =========================== 工具函数：比较结果 ===========================
func equal(a, b []interface{}) bool {
	if len(a) != len(b) {
		return false
	}
	for i := range a {
		if a[i] != b[i] {
			return false
		}
	}
	return true
}

// =========================== 测试 ===========================
func main() {
	fmt.Println("=== LeetCode 116: 填充每个节点的下一个右侧节点指针 ===\n")

	testCases := []struct {
		name     string
		root     *Node
		expected []interface{}
	}{
		{
			name:     "空树",
			root:     arrayToTreeLevelOrder([]interface{}{}),
			expected: []interface{}{},
		},
		{
			name:     "单节点",
			root:     arrayToTreeLevelOrder([]interface{}{1}),
			expected: []interface{}{1, "#"},
		},
		{
			name:     "两层树",
			root:     arrayToTreeLevelOrder([]interface{}{1, 2, 3}),
			expected: []interface{}{1, "#", 2, 3, "#"},
		},
		{
			name:     "三层完美二叉树",
			root:     arrayToTreeLevelOrder([]interface{}{1, 2, 3, 4, 5, 6, 7}),
			expected: []interface{}{1, "#", 2, 3, "#", 4, 5, 6, 7, "#"},
		},
		{
			name:     "四层完美二叉树",
			root:     arrayToTreeLevelOrder([]interface{}{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}),
			expected: []interface{}{1, "#", 2, 3, "#", 4, 5, 6, 7, "#", 8, 9, 10, 11, 12, 13, 14, 15, "#"},
		},
	}

	methods := []struct {
		name string
		fn   func(*Node) *Node
	}{
		{"方法一：BFS层序遍历", connect1},
		{"方法二：递归连接", connect2},
		{"方法三：迭代O(1)空间", connect3},
		{"方法四：DFS前序遍历", connect4},
	}

	allPassed := true
	for _, method := range methods {
		fmt.Printf("--- %s ---\n", method.name)
		passed := 0
		for i, tc := range testCases {
			// 重新构建树（因为会修改原树）
			testRoot := arrayToTreeLevelOrder(getTreeArray(tc.name))
			result := method.fn(testRoot)
			got := levelOrderWithNext(result)

			if equal(got, tc.expected) {
				fmt.Printf("  Test %d: ✓ PASSED\n", i+1)
				passed++
			} else {
				fmt.Printf("  Test %d: ✗ FAILED\n", i+1)
				fmt.Printf("    输入: %v\n", getTreeArray(tc.name))
				fmt.Printf("    期望: %v\n", tc.expected)
				fmt.Printf("    得到: %v\n", got)
				allPassed = false
			}
		}
		fmt.Printf("通过率: %d/%d\n\n", passed, len(testCases))
	}

	if allPassed {
		fmt.Println("🎉 所有测试通过！")
	} else {
		fmt.Println("❌ 部分测试失败")
	}
}

// 辅助函数：根据测试用例名称获取树数组
func getTreeArray(name string) []interface{} {
	switch name {
	case "空树":
		return []interface{}{}
	case "单节点":
		return []interface{}{1}
	case "两层树":
		return []interface{}{1, 2, 3}
	case "三层完美二叉树":
		return []interface{}{1, 2, 3, 4, 5, 6, 7}
	case "四层完美二叉树":
		return []interface{}{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}
	default:
		return []interface{}{}
	}
}
相关推荐
郝学胜-神的一滴1 小时前
贝叶斯之美：从公式到朴素贝叶斯算法的实践之旅
人工智能·python·算法·机器学习·scikit-learn
静心观复1 小时前
贝叶斯公式拆解
算法
智者很聪明1 小时前
排序算法—冒泡排序
算法·排序算法
AC赳赳老秦1 小时前
云原生AI趋势：DeepSeek与云3.0架构协同，提升AI部署性能与可移植性
大数据·前端·人工智能·算法·云原生·架构·deepseek
gorgeous(๑>؂<๑）2 小时前
【ICLR26-Oral Paper-Meta】先见之明：揭秘语言预训练中大型语言模型的视觉先验
人工智能·深度学习·算法·机器学习·语言模型
tod1132 小时前
力扣基础算法分类刷题：位运算、数学、数组与字符串详解
算法·leetcode·职场和发展
ValhallaCoder2 小时前
hot100-图论
数据结构·python·算法·图论
熬了夜的程序员2 小时前
【LeetCode】118. 杨辉三角
linux·算法·leetcode
智算菩萨2 小时前
规模定律的边际递减与后训练时代的理论重构
人工智能·算法
热门推荐
01GitHub 镜像站点02Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services03openclaw配置教程（linux+局域网ollama）04UV安装并设置国内源05Linux下V2Ray安装配置指南06【软考经验分享】软考-中级-嵌入式备考07243 行 microGPT：把“训练 + 推理”拆到骨头里08AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南09Spring Flux方法总结10openclaw使用nginx反代部署过程 与disconnected (1008): pairing required解决