硅基计划4.0 算法简单实现B树

文章目录

- 一、原理
- 二、实现代码

一、原理

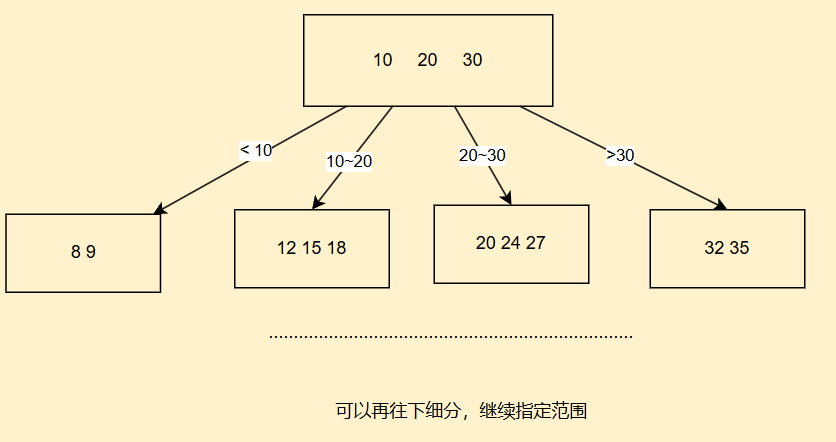
二、实现代码

java 复制代码

package BTree;

/**
 * @author pluchon
 * @create 2026-02-12-13:31
 * 作者代码水平一般，难免难看，请见谅
 */
public class Pair<K,V> {
    private K key;
    private V value;

    public Pair(K key, V value) {
        this.key = key;
        this.value = value;
    }

    public K getKey() {
        return key;
    }

    public void setKey(K key) {
        this.key = key;
    }

    public V getValue() {
        return value;
    }

    public void setValue(V value) {
        this.value = value;
    }
}

java 复制代码

package BTree;

import java.util.Arrays;

/**
 * @author pluchon
 * @create 2026-02-12
 * 作者代码水平一般，难免难看，请见谅
 */
//简单模拟实现B树
public class MyBTree {
    static class BTreeNode{
        //关键字数组
        private int [] keys;
        //双亲引用
        private BTreeNode parent;
        //孩子数组
        private BTreeNode [] childs;
        //该节点的有效关键字个数
        private int usedSize;
        //为了便于分裂，我们设计多流出一个空间
        public BTreeNode(int capacity) {
            this.keys = new int[capacity];
            this.childs = new BTreeNode[capacity+1];
            this.usedSize = 0;
            DEFAULT_KEYS_COUNT = capacity;
        }
        public BTreeNode() {
            this(DEFAULT_KEYS_COUNT);
        }
    }

    //默认是三叉数
    public static int DEFAULT_KEYS_COUNT = 3;

    //根节点
    private BTreeNode root;

    //插入部分
    public boolean insert(int key) {
        //查看根节点是否为空
        if(root == null){
            root = new BTreeNode(DEFAULT_KEYS_COUNT);
            root.keys[0] = key;
            root.usedSize++;
            return true;
        }
        //如果根节点不为空，看当前key值是否已经存在
        Pair<BTreeNode, Integer> result = find(key);
        if(result.getValue() != -1){
            return false;
        }
        //开始正式插入
        BTreeNode parent = result.getKey();
        //先把当前节点进行插入排序
        insertkey(parent, key);
        //插入完毕后判断有没有满
        if(parent.usedSize >= DEFAULT_KEYS_COUNT){
            split(parent);
        }
        return true;
    }

    //寻找该key值是否已经插入
    public Pair<BTreeNode,Integer> find(int key){
        BTreeNode parent = null;
        BTreeNode current = root;
        while(current != null){
            int index = 0;
            while(index < current.usedSize){
                if(current.keys[index] == key){
                    return new Pair<>(current,index);
                }else if(current.keys[index] < key){
                    index++;
                }else{
                    break;
                }
            }
            parent = current;
            current = current.childs[index];
        }
        return new Pair<>(parent,-1);
    }

    //插入key值，也就是插入排序
    private void insertkey(BTreeNode node,int key){
        int index = node.usedSize-1;
        while(index >= 0){
            if(node.keys[index] >= key){
                node.keys[index+1] = node.keys[index];
            }else{
                break;
            }
            index--;
        }
        node.keys[index+1] = key;
        node.usedSize++;
    }

    //分裂逻辑
    private void split(BTreeNode current){
        int middle = current.usedSize/2;
        int middleValue = current.keys[middle];
        BTreeNode newNode = new BTreeNode();
        BTreeNode parent = current.parent;
        //复制右半部分到新节点
        int newIndex = 0;
        for(int i = middle+1; i < current.usedSize; i++){
            newNode.keys[newIndex] = current.keys[i];
            newNode.childs[newIndex] = current.childs[i];
            if(newNode.childs[newIndex] != null){
                newNode.childs[newIndex].parent = newNode;
            }
            newIndex++;
        }
        newNode.childs[newIndex] = current.childs[current.usedSize];
        if(newNode.childs[newIndex] != null){
            newNode.childs[newIndex].parent = newNode;
        }
        newNode.usedSize = current.usedSize - middle - 1;
        //清理current右半部分
        for(int i = middle; i < DEFAULT_KEYS_COUNT; i++){
            current.keys[i] = 0;
        }
        for(int i = middle+1; i < DEFAULT_KEYS_COUNT+1; i++){
            current.childs[i] = null;
        }
        current.usedSize = middle;
        if(current == root){
            root = new BTreeNode();
            root.keys[0] = middleValue;
            root.childs[0] = current;
            root.childs[1] = newNode;
            root.usedSize = 1;
            current.parent = root;
            newNode.parent = root;
            return;
        }
        newNode.parent = parent;
        int parentIndex = parent.usedSize-1;
        while(parentIndex >= 0){
            if(parent.keys[parentIndex] >= middleValue){
                parent.keys[parentIndex+1] = parent.keys[parentIndex];
                parent.childs[parentIndex+2] = parent.childs[parentIndex+1];
            }else{
                break;
            }
            parentIndex--;
        }
        parent.keys[parentIndex+1] = middleValue;
        parent.childs[parentIndex+2] = newNode;
        parent.usedSize++;
        if(parent.usedSize >= DEFAULT_KEYS_COUNT){
            split(parent);
        }
    }

    //===================== 删除部分 =====================
    public boolean remove(int key){
        Pair<BTreeNode, Integer> result = find(key);
        if(result.getValue() == -1){
            return false;
        }
        BTreeNode node = result.getKey();
        int index = result.getValue();
        //如果删除的是非叶子节点
        if(node.childs[0] != null){
            //寻找右子树中的最小值作为后继
            BTreeNode successor = node.childs[index+1];
            while(successor.childs[0] != null){
                successor = successor.childs[0];
            }
            //用后继覆盖当前key
            node.keys[index] = successor.keys[0];
            node = successor;
            index = 0;
        }
        deleteEntry(node,index);
        return true;
    }

    //真正删除叶子节点中的key
    private void deleteEntry(BTreeNode node,int index){
        //移动key
        for(int i = index; i < node.usedSize-1; i++){
            node.keys[i] = node.keys[i+1];
        }
        //移动child
        for(int i = index+1; i <= node.usedSize; i++){
            node.childs[i-1] = node.childs[i];
        }
        node.childs[node.usedSize] = null;
        node.keys[node.usedSize-1] = 0;
        node.usedSize--;
        int minKeys = (DEFAULT_KEYS_COUNT+1)/2 - 1;
        if(node != root && node.usedSize < minKeys){
            fixAfterDeletion(node);
        }
        if(node == root && node.usedSize == 0){
            root = node.childs[0];
            if(root != null){
                root.parent = null;
            }
        }
    }

    //删除后修复
    private void fixAfterDeletion(BTreeNode node){
        BTreeNode parent = node.parent;
        int idx = -1;
        for(int i = 0; i <= parent.usedSize; i++){
            if(parent.childs[i] == node){
                idx = i;
                break;
            }
        }
        if(idx == -1){
            throw new RuntimeException("Structure Corrupted");
        }
        int minKeys = (DEFAULT_KEYS_COUNT+1)/2 - 1;
        //向左借
        if(idx > 0 && parent.childs[idx-1].usedSize > minKeys){
            borrowFromLeft(node,parent.childs[idx-1],parent,idx);
        }
        //向右借
        else if(idx < parent.usedSize && parent.childs[idx+1].usedSize > minKeys){
            borrowFromRight(node,parent.childs[idx+1],parent,idx);
        }
        //合并
        else{
            if(idx > 0){
                merge(parent.childs[idx-1],node,parent,idx-1);
            }else{
                merge(node,parent.childs[idx+1],parent,idx);
            }
        }
    }

    private void borrowFromLeft(BTreeNode node,BTreeNode left,BTreeNode parent,int idx){
        for(int i = node.usedSize; i > 0; i--){
            node.keys[i] = node.keys[i-1];
        }
        for(int i = node.usedSize+1; i > 0; i--){
            node.childs[i] = node.childs[i-1];
        }
        node.keys[0] = parent.keys[idx-1];
        node.childs[0] = left.childs[left.usedSize];
        if(node.childs[0] != null){
            node.childs[0].parent = node;
        }
        parent.keys[idx-1] = left.keys[left.usedSize-1];
        left.childs[left.usedSize] = null;
        left.usedSize--;
        node.usedSize++;
    }

    private void borrowFromRight(BTreeNode node,BTreeNode right,BTreeNode parent,int idx){
        node.keys[node.usedSize] = parent.keys[idx];
        node.childs[node.usedSize+1] = right.childs[0];
        if(node.childs[node.usedSize+1] != null){
            node.childs[node.usedSize+1].parent = node;
        }
        parent.keys[idx] = right.keys[0];
        for(int i = 0; i < right.usedSize-1; i++){
            right.keys[i] = right.keys[i+1];
        }
        for(int i = 0; i < right.usedSize; i++){
            right.childs[i] = right.childs[i+1];
        }
        right.childs[right.usedSize] = null;
        right.usedSize--;
        node.usedSize++;
    }

    private void merge(BTreeNode left,BTreeNode right,BTreeNode parent,int parentIdx){
        left.keys[left.usedSize] = parent.keys[parentIdx];
        int start = left.usedSize+1;
        for(int i = 0; i < right.usedSize; i++){
            left.keys[start+i] = right.keys[i];
            left.childs[start+i] = right.childs[i];
            if(left.childs[start+i] != null){
                left.childs[start+i].parent = left;
            }
        }
        left.childs[start+right.usedSize] = right.childs[right.usedSize];
        if(left.childs[start+right.usedSize] != null){
            left.childs[start+right.usedSize].parent = left;
        }
        left.usedSize += right.usedSize+1;
        for(int i = parentIdx; i < parent.usedSize-1; i++){
            parent.keys[i] = parent.keys[i+1];
            parent.childs[i+1] = parent.childs[i+2];
        }
        parent.childs[parent.usedSize] = null;
        parent.usedSize--;
        int minKeys = (DEFAULT_KEYS_COUNT+1)/2 - 1;
        //如果parent是根节点
        if(parent == root){
            if(parent.usedSize == 0){
                root = left;
                root.parent = null;
            }
            //根节点处理完直接结束
            return;
        }
        //如果不是根节点，才允许继续向上修复
        if(parent.usedSize < minKeys){
            fixAfterDeletion(parent);
        }
    }

    public void printTree() {
        if (root == null) return;
        System.out.print("B-Tree 中序: ");
        inOrder(root);
        System.out.println("\n根节点内容: " + Arrays.toString(Arrays.copyOf(root.keys, root.usedSize)));
    }

    private void inOrder(BTreeNode node) {
        if (node == null) return;
        for (int i = 0; i < node.usedSize; i++) {
            inOrder(node.childs[i]);
            System.out.print(node.keys[i] + " ");
        }
        inOrder(node.childs[node.usedSize]);
    }

    // --- 测试用例 ---
    public static void main(String[] args) {
        MyBTree btree = new MyBTree();
        // 构造一个 3 阶 B 树 (2-3树)
        int[] data = {10, 20, 30, 40, 50, 60, 70};
        for (int x : data) btree.insert(x);
        System.out.println("====== B树测试 ======");
        btree.printTree();
        System.out.println("\n[场景1] 删除 70:");
        btree.remove(70); btree.printTree();
        System.out.println("\n[场景2] 删除 60:");
        btree.remove(60); btree.printTree();
        System.out.println("\n[场景3] 删除 50:");
        btree.remove(50); btree.printTree();
        System.out.println("\n全部删除测试通过！");
    }
}

感谢你的阅读

硅基计划4.0 算法 简单实现B树

文章目录

一、原理

二、实现代码

硅基计划4.0 算法简单实现B树