🔥近津薪荼： [个人主页] 🎬个人专栏： 《近津薪荼的算法日迹》 《Linux操作系统及网络基础知识分享》 《c++基础知识详解》 《c语言基础知识详解》 ✨不要物化，矮化，弱化，钝化自己，保持锋芒，不要停止学习 这个世界上只有两个人真正在注意着你 八岁的你，和八十岁的你， 他们此刻正在注视着你， 一个希望你 勇敢开始 ，一个希望你 不留遗憾
1.上期参考代码
cpp
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int n=nums.size();
vector<int>front(n,1);
for (int i=1;i<n;i++)
{
front[i]=front[i-1]*nums[i-1];
}
vector<int>back(n,1);
for (int i=n-2;i>=0;i--)
{
back[i]=back[i+1]*nums[i+1];
}
vector<int>ret(n);
for(int i=0;i<n;i++)
{
ret[i]=front[i]*back[i];
}
return ret;
}
};2.本期知识点导图
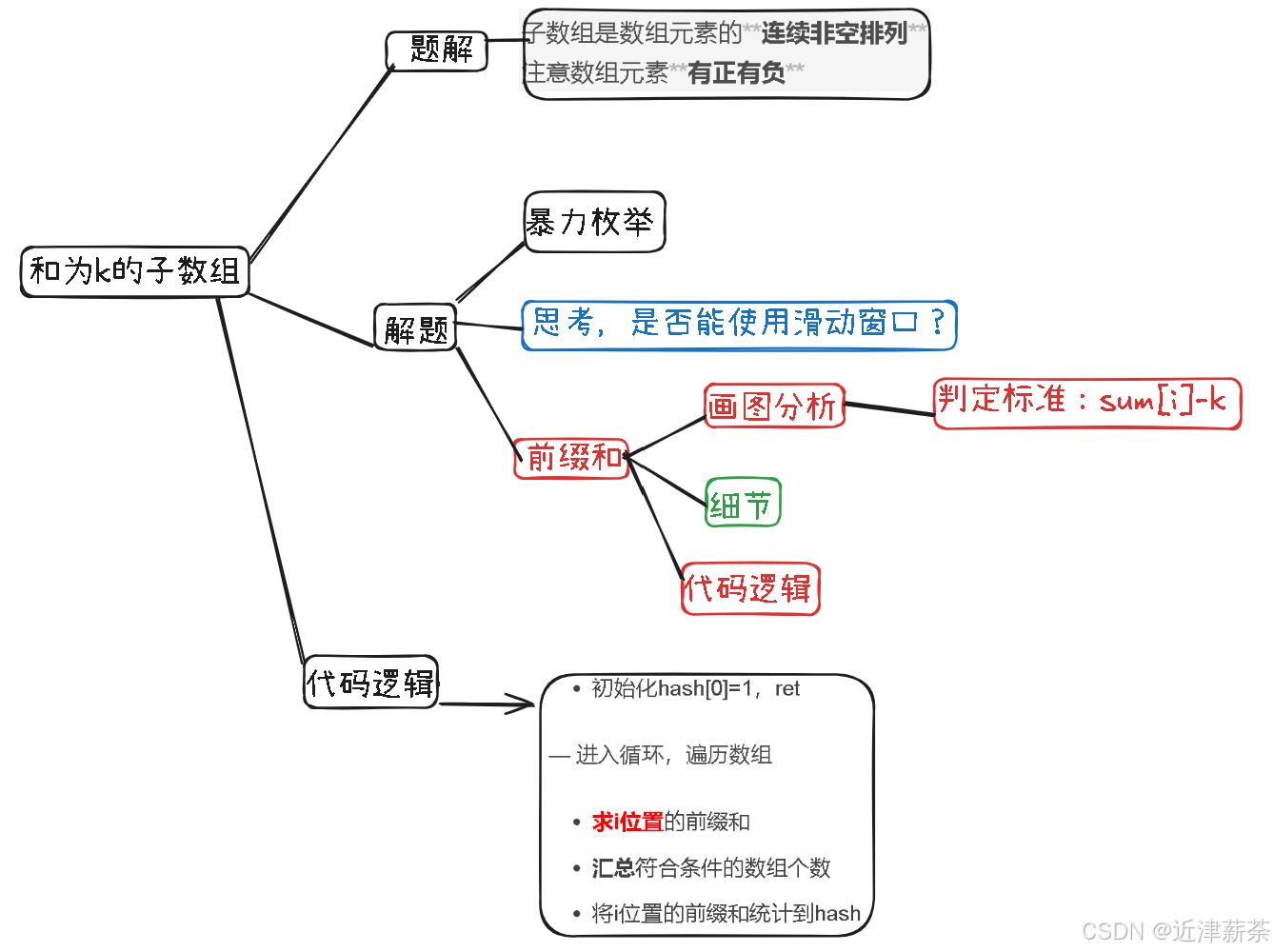
3.本期要讲解的题目是
和为 K 的子数组
要点：
- 子数组是数组元素的连续非空排列
- 注意数组元素有正有负
4.解题
4.1 暴力解法：
暴力枚举，算出所有子数组的和，需嵌套3层循环，时间复杂度O(N3)（前两层枚举子数组左右区间，里层数组求和）
4.2优解
思考
联系我们之前做过双指针，滑动窗口的题，寻找符合条件的子数组，我们这道题目可以使用吗？
使用双指针解决问题是利用双指针的不回退来降低遍历数组的时间复杂度 ，其要依赖窗口信息的单调性来实现
本题数组元素包含0和负数，导致求和（窗口信息）不具有单调性了！
我们思考能否由我们自己塑造单调性呢，显然做不到，目前我们塑造单调性，只使用过排序，然而排序并不能解决求和的单调性问题
双指针的思路只能放弃
对于数组求和，我们还接接触过一种算法：前缀和
前缀和
用前缀和，就别管那么多了，直接在数组前n项和的变式上，摸索摸索
如图：我们将数组抽象成一个线条方便画图
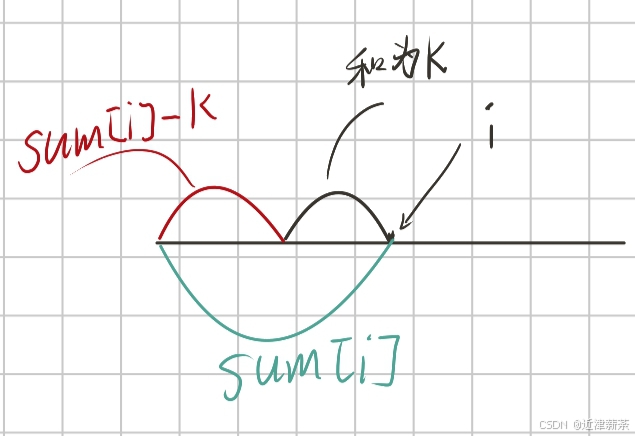
画完发现像个嘴唇
上图中，是对于数组中随机的一个符合条件的子数组进行的分析
图中子数组的右区间是 i
我们发现子数组和为k，那么它前边的区间部分的和，必然是sum[ i ]-k
核心思想
那么我们就可以推出，对于数组的前i项，其前缀和数组中存在值为sum[ i ]-k的话，必然存在一个子数组，它的和为k
我们要统计 和为k的子数组的个数，即统计i之前的数组的前缀和为sum[i]-k的个数，使用hash表即可，统计完之后，把它累加给ret即可
细节
- 不可以也没必要一次性把所有的前缀和全部算出来，因为在i之后，有新的元素的加入，可能还会有满足前缀和为sum[i]-k的位置出现，比如i+1的位置为-1，i+2的位置为1。sum[i+2]-k等于sum[i]-k，但是它的位置就不对了，没有对应的和为k的子数组，但是我们统计的标准是统计前缀和为sum[i]-k，hash会把它统计到，属于无效统计。
- 在前i-1个位置的前缀和中汇总数组的前缀和为sum[i]-k的个数，然后再把sum[i]加入到哈希表中，这是为了防止k=0时的误判，若k=0，先将sum[i]加入到哈希表，不管是否有和为0的子数组，sum[i]必然满足与sum[i]-k相等的条件，这样我们的判断标准就失灵了。
- 如果sum[i]本身就为k，那么sum[i]-k等于0，那么sum[i]也是满足条件的，但是我们hash只统计前i-1个位置，所以在开始之前，hash[0]的值就应该是1。
代码逻辑：
- 初始化hash[0]=1，ret
--- 进入循环，遍历数组
- 求i位置的前缀和
- 汇总符合条件的数组个数
- 将i位置的前缀和统计到hash
5.下期要讲解的题目是：
和可被 K 整除的子数组
6.嗟食
如果小编写的内容对佬有帮助，还请大佬点点三连加关注哦 
佬的支持就是我前进的最大动力 
~
期待与佬的再次相遇~