Java算法实践（二）：堆与PriorityQueue实战

在 Java 后端开发中，我们常用 PriorityQueue 来做任务调度（延迟队列）、日志合并、或者系统限流中的滑动窗口统计。而在算法面试中，它是解决 Top K、中位数、合并 K 个有序链表等问题的唯一最优解。

一、认识堆（Heap）与 PriorityQueue

1.1 什么是堆？为什么它快？

虽然 Java 的 PriorityQueue 实现了 Queue 接口，但它和 LinkedList 或 ArrayDeque 有本质区别。

物理结构 ：它底层是一个动态数组 （Object[] queue）。
逻辑结构 ：它是一棵完全二叉树。
核心性质 ：
- 小顶堆（Min-Heap，Java默认） ：任意节点的值 ≤ \le ≤ 其左右子节点的值。这意味着，堆顶（数组索引0）永远是整个堆中最小的元素。
- 大顶堆（Max-Heap） ：任意节点的值 ≥ \ge ≥ 其左右子节点的值。堆顶是最大值。

为什么不用 Arrays.sort()？

如果你有一个包含 100万个元素的数组，想找到前 10 大的数：

排序法 ：Arrays.sort() 基于双轴快排或 TimSort，时间复杂度是 O ( N log ⁡ N ) O(N \log N) O(NlogN)。
堆解法 ：维护一个大小为 10 的堆，遍历数组。复杂度是 O ( N log ⁡ K ) O(N \log K) O(NlogK)。
当 N N N 极大而 K K K 极小时（例如海量日志处理），堆的性能优势是降维打击级别的。

1.2 Java 实战中避坑

在使用 PriorityQueue 解题前，必须牢记以下三点：

无序性 ：除了堆顶，堆内其他元素的顺序是不可预测 的。不要尝试用 for (int x : pq) 去打印堆来看顺序。只有不断 poll() 出来的序列才是有序的。
不允许 Null ：插入 null 会直接抛出 NPE。
对象比较 ：存入的对象必须是可比较的（Comparable），或者在构造时传入 Comparator。

关于 PriorityQueue 的介绍在上一篇有简单讲解，这里不过多介绍。

二、核心模式：Top K 问题（堆的高频应用）

这是堆结构在算法面试与后端实际开发（如热搜榜单、日志监控）中出现率最高的场景。理解 Top K 问题的本质，是掌握堆数据结构的关键。

2.1 解析：为什么求"前 K 大"必须用"小顶堆"？

这是一个初学者极易混淆的反直觉设计。

通常解决"前 K 大"问题有三种思路，我们来对比一下：

全局排序法：
- 直接对数组进行 Arrays.sort()，然后取最后 K 个元素。
- 缺点：时间复杂度为 O ( N log ⁡ N ) O(N \log N) O(NlogN)。当数据量 N N N 非常大（如海量日志）而 K K K 很小（如前 10 条）时，对所有数据排序是极大的资源浪费。
大顶堆（Max-Heap）法（直觉思路）：
- 构建一个包含所有 N N N 个元素的大顶堆，然后执行 K K K 次 poll() 操作。
- 缺点：
  - 空间复杂度 ： O ( N ) O(N) O(N)。需要把所有数据加载到内存中构建堆。如果是处理海量数据，内存可能溢出。
  - 建堆时间 ：初始化建堆需要 O ( N ) O(N) O(N)。
小顶堆（Min-Heap）法（最优解）：
- 维护一个容量仅为 K 的小顶堆。这个堆的作用是**"过滤器"**，它只保留目前为止见过的最大的 K 个数。
- 核心逻辑 ：
  - 堆顶（Root）存放的是这 K 个数中的最小值。
  - 当遍历到一个新元素 x 时，将其与堆顶比较。
  - 如果 x > 堆顶：说明 x 比堆里最小的元素要大，它有资格进入前 K 名。此时将堆顶（最小的元素）移出堆，将 x 放入堆中。
  - 如果 x <= 堆顶：说明 x 连目前前 K 名里最小的都小，直接丢弃，无需入堆。
- 结果：遍历结束后，堆中留下的 K 个元素就是最大的 K 个数，而堆顶正是第 K 大的数。

结论总结：

求 Top K Largest （前 K 大） → \rightarrow → 使用 Min-Heap（小顶堆），保留较大的数，挤出最小的数。
求 Top K Smallest （前 K 小） → \rightarrow → 使用 Max-Heap（大顶堆），保留较小的数，挤出最大的数。

2.2 实战演练：数组中的第K个最大元素

题目链接 ：LeetCode 215. Kth Largest Element in an Array

题目描述 ：给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

1. 解题代码

java 复制代码

public int findKthLargest(int[] nums, int k) {
    // 初始化小顶堆
    // Java 的 PriorityQueue 默认即为小顶堆 (Min-Heap)
    PriorityQueue<Integer> minHeap = new PriorityQueue<>();

    // 遍历数组
    for (int num : nums) {
        // 核心逻辑：维护堆的大小不超过 K
        if (minHeap.size() < k) {
            // 如果堆还没满，直接放入
            minHeap.offer(num);
        } else {
            // 如果堆已满（size == k），比较当前元素与堆顶
            // 如果新元素比堆顶大，说明堆顶元素不配在前 K 大之列，将其替换
            if (num > minHeap.peek()) {
                minHeap.poll(); // 弹出最小值
                minHeap.offer(num); // 压入新值
            }
            // 如果 num <= minHeap.peek()，则忽略该元素
        }
    }

    // 遍历结束，堆中包含 nums 中最大的 k 个元素
    // 根据小顶堆性质，堆顶即为这 k 个数中的最小值（也就是第 k 大的数）
    return minHeap.peek();
}

2. 代码执行过程推演

假设输入数组 nums = [3, 2, 1, 5, 6, 4]，k = 2。我们需要找第 2 大的数。

步骤	当前元素	操作描述	堆的状态 (堆顶在左)	逻辑解释
1	`3`	堆未满，直接入堆	`[3]`	目前前 2 大是 {3}
2	`2`	堆未满，直接入堆	`[2, 3]`	目前前 2 大是 {3, 2}，堆顶是 2
3	`1`	堆已满。比较 `1` 与堆顶 `2`。`1 < 2`	`[2, 3]`	1 比前 2 名里最小的还小，直接丢弃
4	`5`	堆已满。`5 > 2`	`[3, 5]`	5 比堆顶 2 大。2 出局，5 入局。堆重新调整，3 成为新堆顶
5	`6`	堆已满。`6 > 3`	`[5, 6]`	6 比堆顶 3 大。3 出局，6 入局。堆重新调整，5 成为新堆顶
6	`4`	堆已满。`4 < 5`	`[5, 6]`	4 比堆顶 5 小，无法进入前 2 名，丢弃
结束	-	返回堆顶	`5`	最终堆里是 {5, 6}，第 2 大的是 5

通过推演可以看到，小顶堆始终维持着一个"高水平"的集合，任何试图进入该集合的元素都必须进行"比当前集合最小值还要大"的比较。

2.3 复杂度与性能分析

时间复杂度： O ( N log ⁡ K ) O(N \log K) O(NlogK)

解释：我们需要遍历数组中的每一个元素，共 N N N 次。
在最坏情况下，每个元素都需要进行入堆/出堆操作。
堆的大小被严格限制为 K K K。在大小为 K K K 的堆中插入或删除元素的时间复杂度是 O ( log ⁡ K ) O(\log K) O(logK)。
因此总耗时为 N × log ⁡ K N \times \log K N×logK。
对比：当 K K K 远小于 N N N 时（例如在 10亿数据中找前 100 大）， log ⁡ K \log K logK 几乎可以看作常数， O ( N log ⁡ K ) O(N \log K) O(NlogK) 趋近于 O ( N ) O(N) O(N)（线性时间），这远优于排序算法的 O ( N log ⁡ N ) O(N \log N) O(NlogN)。

空间复杂度： O ( K ) O(K) O(K)

解释：我们只维护了一个容量为 K K K 的优先队列，无论输入数组 N N N 有多大，内存占用仅与 K K K 相关。
优势：这是处理海量数据 或无限流式数据 的关键。如果 N N N 是 1TB 的日志文件，我们无法将其全部读入内存排序，但 O ( K ) O(K) O(K) 的堆空间（也许只有几 KB）可以轻松放入内存。

2.4 JDK API 的简化写法

为了追求代码简洁，我们常将入堆逻辑简化。虽然性能上略有损耗（多了一次无谓的入堆再出堆），但在算法题的数据规模下通常可忽略。

简化版代码：

java 复制代码

public int findKthLargest(int[] nums, int k) {
    PriorityQueue<Integer> pq = new PriorityQueue<>();
    for (int val : nums) {
        pq.offer(val); // 无论如何先放入
        if (pq.size() > k) { // 只要超标，立刻剔除最小的
            pq.poll();
        }
    }
    return pq.peek();
}

这种写法代码更少，更易记忆。

三、进阶模式：键值对与频率统计

LeetCode 中有一类题不直接比较数字大小，而是比较数字出现的频率、距离或者对象的某个组合属性 。这类问题通常无法直接将原始数据放入堆中，需要结合 HashMap 进行预处理，并使用自定义 Comparator 来定义堆的"优先级"。

3.1 实战例题：前 K 个高频元素

题目链接 ：LeetCode 347. Top K Frequent Elements

题目描述：给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。

解题思路：

统计频率 ：先用 HashMap 统计每个数出现的次数，构建 <数字, 频率> 的映射。
入堆筛选 ：我们需要频率最高的 K K K 个。根据上一节的理论，维护"精英俱乐部"需要使用小顶堆来剔除频率低的元素（让频率最低的在堆顶，随时准备被淘汰）。
自定义比较器：堆里存的是数字（Key），但比较的依据是 Map 中的频率（Value）。

代码实现：

java 复制代码

public int[] topKFrequent(int[] nums, int k) {
    // 使用 HashMap 统计频率: Map<数字, 频率>
    Map<Integer, Integer> countMap = new HashMap<>();
    for (int n : nums) {
        countMap.put(n, countMap.getOrDefault(n, 0) + 1);
    }

    // 创建小顶堆
    // 关键点：Comparator 比较的是 countMap 中的 value（频率）
    PriorityQueue<Integer> minHeap = new PriorityQueue<>((n1, n2) -> countMap.get(n1) - countMap.get(n2));

    // 遍历 Map 的 Key（即去重后的数字）
    for (int num : countMap.keySet()) {
        minHeap.offer(num);
        
        // 维护堆大小为 k
        if (minHeap.size() > k) {
            // 堆顶是当前堆里频率最低的，将其移出
            minHeap.poll();
        }
    }

    // 取出结果
    int[] res = new int[k];
    // 注意：直接 poll 出来的是频率从小到大的
    for (int i = 0; i < k; i++) {
        res[i] = minHeap.poll();
    }
    return res;
}

3.2 Comparator 的多维排序规则（Tie-breaking）

在实际中可能不会只按单一条件（如频率）排序，而是会增加**"次要条件"**（Tie-breaker）。

常见场景：

"找出频率最高的 K 个单词。如果两个单词频率相同，按字典序更小的排在前面。"（参考 LeetCode 692. Top K Frequent Words）

如果直接照搬上面的代码，通过 countMap.get(w1) - countMap.get(w2) 只能解决频率问题，无法处理频率相同的情况。此时需要编写更复杂的 Comparator。

逻辑推导：

主要条件 ：按频率。需要取Top K 高频 ，所以用小顶堆 剔除低频。
- 堆顶应该是频率最低的。
次要条件 ：按字典序。题目要求频率相同时，字典序更小的优先（即字典序小的算"大/强"）。
- 在小顶堆的"淘汰"逻辑中，应该保留"强"的，剔除"弱"的。
- 如果频率相同，我们要保留字典序小的，那么堆顶（将被踢走的）应该是字典序更大的那个。所以这里应该使用大顶堆。

多维 Comparator 写法：

java 复制代码

PriorityQueue<String> pq = new PriorityQueue<>((w1, w2) -> {
    int count1 = countMap.get(w1);
    int count2 = countMap.get(w2);
    
    if (count1 != count2) {
        // 频率不同：按频率升序（小顶堆逻辑，频率低的在堆顶）
        return count1 - count2;
    } else {
        // 频率相同：按字典序降序（注意！这里反过来了）
        // 为什么要降序？因为我们要保留字典序小的。
        return w2.compareTo(w1);
    }
});

3.3 使用 `Map.Entry` 或自定义类

在 3.1 的代码中，我们直接将 Integer（数字）放入堆中，每次比较时都要去 HashMap 中执行 get() 操作。虽然哈希表的查找平均是 O ( 1 ) O(1) O(1)，但在频繁的比较中，不断的哈希计算和寻址依然会有性能损耗。

优化方案 ：

将 Key 和 Value 打包成一个对象放入堆中。Java 提供了现成的 Map.Entry，或者可以写一个简单的 POJO。

优化后的写法（更推荐的工程写法）：

java 复制代码

// 泛型写法，堆里直接存 Entry 对象，避免重复查表
PriorityQueue<Map.Entry<Integer, Integer>> pq = new PriorityQueue<>(
    (a, b) -> a.getValue() - b.getValue() // 直接比较 Value，速度更快
);

for (Map.Entry<Integer, Integer> entry : countMap.entrySet()) {
    pq.offer(entry);
    if (pq.size() > k) {
        pq.poll();
    }
}

这种写法的优点：

性能更好 ：避免了 Comparator 内部重复的哈希查找。
代码更清晰：数据本身就包含了比较所需的所有信息，解耦了堆和 Map。
扩展性强：如果以后需要按照三个条件排序，只需扩展 Entry 或者自定义类即可，无需依赖外部 Map。

四、高级模式：双堆对撞（动态中位数）

如果一个问题需要动态维护数据的"中间位置"，或者动态获取最大和最小值，通常需要两个堆配合使用。

4.1 核心理念：沙漏模型

可以把所有数据想象成在一个沙漏中流动。为了随时找到中位数，我们将数据流在中间切开，分为两半：

下半区（Left / Max-Heap） ：存放数据流中较小的一半。为了能随时摸到这部分最大的那个，需要用大顶堆。
上半区（Right / Min-Heap） ：存放数据流中较大的一半。为了能随时摸到这部分最小的那个，需要用小顶堆。

中位数就在这两个堆的堆顶产生：

如果总个数是偶数：中位数是 (Left堆顶 + Right堆顶) / 2.0。
如果总个数是奇数：我们人为规定让 Left 多存一个，中位数就是 Left堆顶。

4.2 实战例题：数据流的中位数

题目链接 ：LeetCode 295. Find Median from Data Stream

题目描述 ：设计一个数据结构，支持 addNum 添加数字，findMedian 返回当前所有数字的中位数。

1. 解题代码

java 复制代码

class MedianFinder {
    // 左半边：大顶堆
    private PriorityQueue<Integer> leftMaxHeap;
    // 右半边：小顶堆
    private PriorityQueue<Integer> rightMinHeap;

    public MedianFinder() {
        // 大顶堆构建：(a, b) -> b - a
        leftMaxHeap = new PriorityQueue<>((a, b) -> Integer.compare(b, a));
        // 小顶堆构建：默认
        rightMinHeap = new PriorityQueue<>();
    }
    
    public void addNum(int num) {
        // 先进左边，再从左边挤一个最大的去右边
        leftMaxHeap.offer(num);
        rightMinHeap.offer(leftMaxHeap.poll());
        
        // 平衡数量：我们要保证 left.size >= right.size
        // 且 size 差距不能超过 1
        if (leftMaxHeap.size() < rightMinHeap.size()) {
            leftMaxHeap.offer(rightMinHeap.poll());
        }
    }
    
    public double findMedian() {
        // 如果 Left 比 Right 多一个，中位数就是 Left 的堆顶
        if (leftMaxHeap.size() > rightMinHeap.size()) {
            return leftMaxHeap.peek();
        } else {
            // 否则两边一样多，取平均值
            return (leftMaxHeap.peek() + rightMinHeap.peek()) / 2.0;
        }
    }
}

2. 流程模拟

这段代码最让人困惑的地方在于 addNum 中的"先左后右再回左"。为什么不能直接判断 num 比中位数大还是小？

模拟输入序列：[41, 35, 62]

输入 41：
- Left 入堆 41 → \rightarrow → Left: [41]
- Left 弹出 41 给 Right → \rightarrow → Left: [], Right: [41]
- 平衡检查 ：Left.size (0) < Right.size (1)，成立。
- Right 弹出 41 给 Left → \rightarrow → Left: [41], Right: []
- 状态：Left 多 1 个，中位数 41。
输入 35：
- Left 入堆 35 → \rightarrow → Left: [41, 35] (堆顶 41)
- Left 弹出 41 给 Right → \rightarrow → Left: [35], Right: [41]
- 平衡检查 ：Left.size (1) < Right.size (1)，不成立。
- 状态：两边平衡，中位数 (35+41)/2 = 38。
输入 62：
- Left 入堆 62 → \rightarrow → Left: [62, 35] (堆顶 62)
- Left 弹出 62 给 Right → \rightarrow → Left: [35], Right: [41, 62] (堆顶 41)
- 平衡检查 ：Left.size (1) < Right.size (2)，成立。
- Right 弹出 41 给 Left → \rightarrow → Left: [41, 35], Right: [62]
- 状态：Left 多 1 个，中位数 41。

通过这种"推拉"操作，我们保证了 Left 永远持有较小的一半，Right 永远持有较大的一半，且两者元素数量差不超过 1。

3. 复杂度分析

时间复杂度 ：
- addNum：涉及 3 次堆操作（入堆/出堆），每次 O ( log ⁡ N ) O(\log N) O(logN)。总体 O ( log ⁡ N ) O(\log N) O(logN)。
- findMedian：直接取堆顶，O ( 1 ) O(1) O(1)。
空间复杂度 ：O ( N ) O(N) O(N)，用于存储所有元素。

五、归并模式：多路归并（K-Way Merge）

当有 K K K 个已经排好序的链表或数组，想把它们合并成一个大的有序列表时，两两合并的效率太低（ O ( N ⋅ K ) O(N \cdot K) O(N⋅K)）。最优解是利用堆来做一个"多路选择器"。

5.1 实战例题：合并K个升序链表

题目链接 ：LeetCode 23. Merge k Sorted Lists

题目描述：给你一个链表数组，每个链表都已经按升序排列。请你将所有链表合并到一个升序链表中。

解题思路：

初始化 ：把 K K K 个链表的头节点（Head）全部放入一个小顶堆。
循环：
- 堆顶一定是当前所有链表中最小的那个节点。
- 弹出堆顶节点，接在结果链表后面。
- 如果这个节点还有 next（下一个节点），把它的 next 放入堆中。
终止：当堆为空时，合并结束。

代码实现：

java 复制代码

public ListNode mergeKLists(ListNode[] lists) {
    if (lists == null || lists.length == 0) return null;

    // 小顶堆，比较节点的值
    PriorityQueue<ListNode> pq = new PriorityQueue<>((a, b) -> a.val - b.val);

    // 将所有非空头节点加入堆
    for (ListNode head : lists) {
        if (head != null) {
            pq.offer(head);
        }
    }

    // 哨兵节点，方便操作链表头
    ListNode dummy = new ListNode(0);
    ListNode tail = dummy;

    // 循环处理
    while (!pq.isEmpty()) {
        // 取出最小节点
        ListNode smallest = pq.poll();
        tail.next = smallest;
        tail = tail.next;

        // 将其后继节点入堆
        if (smallest.next != null) {
            pq.offer(smallest.next);
        }
    }

    return dummy.next;
}

5.2 多路归并的时间复杂度优化

理解多路归并的核心在于理解堆如何优化了"查找最小值"的过程。算法始终维护一个大小为 K K K 的集合，该集合包含了 K K K 条链表当前未被合并的头节点。

从 O ( N ⋅ K ) O(N \cdot K) O(N⋅K) 到 O ( N log ⁡ K ) O(N \log K) O(NlogK) 的演进：

假设我们要合并总共 N N N 个节点，分属于 K K K 条链表。我们需要执行 N N N 次"取出最小值"的操作。

遍历比较：
- 每次要找到最小值，需要遍历 K K K 个链表的头节点。
- 单次查找耗时： O ( K ) O(K) O(K)。
- 总时间复杂度： N × O ( K ) = O ( N K ) N \times O(K) = O(NK) N×O(K)=O(NK)。
- 缺陷：当 K K K 较大时（例如合并 1000 个有序文件），性能急剧下降。
堆解法（PriorityQueue）：
- 利用堆的特性，始终让 K K K 个节点中的最小值处于堆顶。
- 取出最小值 ：poll() 操作，耗时 O ( log ⁡ K ) O(\log K) O(logK)。
- 加入新节点 ：offer() 操作，耗时 O ( log ⁡ K ) O(\log K) O(logK)。
- 总时间复杂度： N × O ( log ⁡ K ) = O ( N log ⁡ K ) N \times O(\log K) = O(N \log K) N×O(logK)=O(NlogK)。
- 优势： O ( log ⁡ K ) O(\log K) O(logK) 远小于 O ( K ) O(K) O(K)，使得算法能够高效处理大规模链表合并。

5.3 流程图解

假设有 3 条链表（ K = 3 K=3 K=3），我们需要合并它们：

L1 : 1 -> 4 -> 5
L2 : 1 -> 3 -> 4
L3 : 2 -> 6

堆（PriorityQueue）始终只存储每条链表当前的头节点。以下是堆内容随操作变化的逻辑视图（假设堆内元素按升序排列以方便理解）：

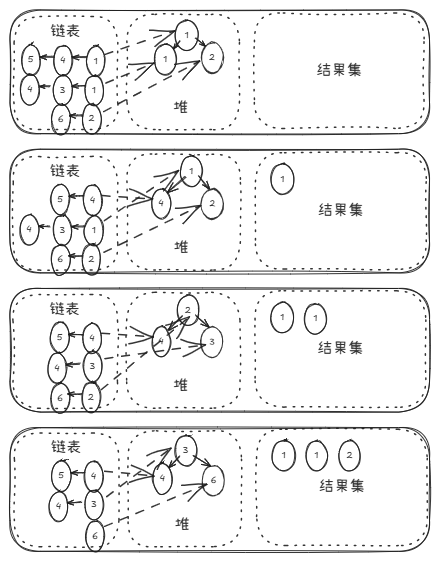
Step 1 : 初始化将 L1, L2, L3 的头节点入堆。堆顶是最小值 1 (来自 L1)。
Step 2 : 弹出 L1 的 1，并将 L1 的下一个节点 4 入堆。堆自动调整，此时最小值是 1 (来自 L2)。
Step 3 : 弹出 L2 的 1，并将 L2 的下一个节点 3 入堆。堆自动调整，此时最小值是 2 (来自 L3)。
Step 4 : 弹出 L3 的 2，并将 L3 的下一个节点 6 入堆。堆自动调整，此时最小值是 3 (来自 L2)。

该过程保证了每次弹出的都是全局最小值，且堆的大小始终维持在 K K K 以内，实现了高效的空间与时间利用。

六、总结与心得

PriorityQueue 是 Java 算法库中极其强大且高效的工具。

题目特征	数据结构选择	核心逻辑
求前 K 大 (Top K Largest)	Min-Heap (小顶堆)	维护前 K 大候选集，踢掉最小的。
求前 K 小 (Top K Smallest)	Max-Heap (大顶堆)	维护前 K 小候选解，踢掉最大的。
求中位数 (Median)	双堆 (Max + Min)	大顶堆存左半部，小顶堆存右半部。
合并 K 个有序结构	Min-Heap	将 K 个头节点入堆，每次取最小并补充 next。
按频率/距离排序	Heap + Comparator	自定义比较器，注意 `a-b` 是升序，`b-a` 是降序。

注意：

在实际后端开发中，PriorityQueue 是非线程安全的。如果你需要在多线程环境下使用堆（例如全局任务调度），使用 java.util.concurrent.PriorityBlockingQueue。算法题不需要。

Java算法实践（二）：堆与PriorityQueue实战

一、 认识堆（Heap）与 PriorityQueue

1.1 什么是堆？为什么它快？

1.2 Java 实战中避坑

二、 核心模式：Top K 问题（堆的高频应用）

2.1 解析：为什么求"前 K 大"必须用"小顶堆"？

2.2 实战演练：数组中的第K个最大元素

1. 解题代码

2. 代码执行过程推演

2.3 复杂度与性能分析

2.4 JDK API 的简化写法

三、 进阶模式：键值对与频率统计

3.1 实战例题：前 K 个高频元素

3.2 Comparator 的多维排序规则（Tie-breaking）

3.3 使用 Map.Entry 或自定义类

四、 高级模式：双堆对撞（动态中位数）

4.1 核心理念：沙漏模型

4.2 实战例题：数据流的中位数

1. 解题代码

2. 流程模拟

3. 复杂度分析

五、 归并模式：多路归并（K-Way Merge）

5.1 实战例题：合并K个升序链表

5.2 多路归并的时间复杂度优化

5.3 流程图解

六、 总结与心得

一、认识堆（Heap）与 PriorityQueue

二、核心模式：Top K 问题（堆的高频应用）

三、进阶模式：键值对与频率统计

3.3 使用 `Map.Entry` 或自定义类

四、高级模式：双堆对撞（动态中位数）

五、归并模式：多路归并（K-Way Merge）

六、总结与心得