当然,读文有感,也算是摘抄一部分,随着慢慢的学习的过程,发现数学真的是一辈子的学科,大学时期真是肤浅了。
避免看不懂,附上原文,文章写的真的挺好,建议都去读读原文。
https://mp.weixin.qq.com/s/MrLlyrdBvDBWyu7LZCHw5Q
其实下面呢,我觉得是极限作为一种新的工具被引入后,我们要定义在上面的很多运算,加减乘除,比较大小,这些都要满足数域上面的封闭,就是说,现在的这套理论不能把之前的数学框架给打破。
极限的引入应该是为了使微积分更有说服力
性质
在哲学/逻辑学上指事物的本质属性,即一事物区别于其他事物的根本特征。在数学上面指图形、函数或数字所具备的特定规律;如"等式的性质"或"三角形的性质"。
也就是说,如果是这个东西,肯定有这个规律。
都上升哲学了,没啥好说的。。。
微分中值定理:函数值与导数之间的核心纽带
微分中值定理体系是连接函数整体变化与局部变化(导数)之间的桥梁 ,在数学分析中占据基础而核心的地位。它不仅奠定了导数几何意义的严格基础,而且是研究函数单调性、极值、凹凸性以及极限理论的重要工具;我觉得更加有趣的一点是,可以从局部变化就能知道整体的变化,这非常de 有用。
罗尔定理(Rolle's Theorem)
设函数 f(x)f(x)f(x) 满足:
在闭区间 [a,b][a,b][a,b] 上连续;在开区间 (a,b)(a,b)(a,b) 内可导;且端点函数值相等:f(a)=f(b)f(a)=f(b)f(a)=f(b)。
则至少存在一点 ξ∈(a,b)\xi \in (a,b)ξ∈(a,b),使得
f′(ξ)=0. f'(\xi)=0. f′(ξ)=0.
在满足端点高度相同的条件下,曲线在区间内部必然存在一条水平切线 ;罗尔定理是整个中值定理体系的基础定理,其余中值定理均可视为它的推广。
只要满足 "连续、光滑、两端等高" 这三个条件,曲线中间必然至少有一个"平"的点。罗尔定理告诉我们:在一个连续光滑的世界里,想要从一个状态回到最初的状态,你必须经历一个"平稳"的瞬间。 无论你是先上升还是先下降,为了回到原点,你必然要在某一刻停下上升或下降的势头。
状态的一种转换
拉格朗日中值定理(Lagrange Mean Value Theorem)
若函数 f(x)f(x)f(x) 在 [a,b][a,b][a,b] 上连续,在 (a,b)(a,b)(a,b) 内可导,则存在 ξ∈(a,b)\xi \in (a,b)ξ∈(a,b),使得
f(b)−f(a)=f′(ξ)(b−a). f(b)-f(a)=f'(\xi)(b-a). f(b)−f(a)=f′(ξ)(b−a).
函数在区间上的平均变化率,等于某一点处的瞬时变化率。
在区间 [a,b][a,b][a,b] 上,至少存在一点,其切线斜率等于割线斜率;当附加条件 f(a)=f(b)f(a)=f(b)f(a)=f(b) 时,拉格朗日中值定理自然退化为罗尔定理。
罗尔定律的升级版,"撤销"了等高的限制。可以想象把罗尔定理的那张图整体旋转了一个角度,它依然成立。
这是拉格朗日定理最出名的生活例子------区间测速:
假设你开车上高速,在 A 收费站(t=at=at=a)领卡,在 B 收费站(t=bt=bt=b)交卡。
- 如果两站距离 120 公里,你花了一个小时跑完。
- 你的平均时速 是 120 km/h120\text{ km/h}120 km/h。
- 拉格朗日定理告诉你:在这一小时里的某一个瞬间 ,你仪表盘上的速度(瞬时速度)一定精确地出现过 120 km/h120\text{ km/h}120 km/h。
如果你平均时速是 130 km/h130\text{ km/h}130 km/h(限速 120),就算你全程没被测速雷达拍到,交警根据拉格朗日定理也能判定你至少在那一瞬间超速了。
柯西中值定理(Cauchy Mean Value Theorem)
设函数 f(x)f(x)f(x) 与 g(x)g(x)g(x) 在 [a,b][a,b][a,b] 上连续、在 (a,b)(a,b)(a,b) 内可导,且 g′(x)≠0g'(x)\neq 0g′(x)=0,则存在 ξ∈(a,b)\xi \in (a,b)ξ∈(a,b),使得
f(b)−f(a)g(b)−g(a)=f′(ξ)g′(ξ). \frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(\xi)}{g'(\xi)}. g(b)−g(a)f(b)−f(a)=g′(ξ)f′(ξ).
柯西中值定理刻画了两个函数变化率之间的比例关系 ,是拉格朗日中值定理在"比值形式"下的推广;它是 洛必达法则 的理论基础。
直观理解:两名赛跑者
想象有两名赛跑者 AAA 和 BBB 在同一段时间 [a,b][a, b][a,b] 内跑步:
- f(t)f(t)f(t) 是跑者 AAA 的位置随时间的变化;
- g(t)g(t)g(t) 是跑者 BBB 的位置随时间的变化。
在整场比赛中,他们的平均速度之比是:
f(b)−f(a)g(b)−g(a) \frac{f(b) - f(a)}{g(b) - g(a)} g(b)−g(a)f(b)−f(a)
柯西中值定理告诉我们:在比赛过程中的某个瞬间 ξ\xiξ,他们瞬时速度的比值 ,正好等于他们全程平均速度的比值。
导数的主要应用方向
导数不仅是局部变化率的刻画工具,更是研究函数整体性质的核心手段。
函数的单调性
若在区间内 f′(x)>0f'(x)>0f′(x)>0,则 f(x)f(x)f(x) 单调递增;若 f′(x)<0f'(x)<0f′(x)<0,则 f(x)f(x)f(x) 单调递减;这是拉格朗日中值定理最直接、最重要的应用之一。
极值与最值问题
通过解方程 f′(x)=0f'(x)=0f′(x)=0 或导数不存在,确定驻点;
利用二阶导数:
f′′(x)>0f''(x)>0f′′(x)>0:极小值;
f′′(x)<0f''(x)<0f′′(x)<0:极大值。
这是函数优化与应用问题的理论基础。
函数的凹凸性与拐点
f′′(x)>0f''(x)>0f′′(x)>0:函数呈凹形(开口向上) ;f′′(x)<0f''(x)<0f′′(x)<0:函数呈凸形(开口向下) ;二阶导数变号的点为拐点;凹凸性决定了函数图形的整体形态。
洛必达法则(L'Hôpital's Rule)
当极限呈现 00\frac{0}{0}00 或 ∞∞\frac{\infty}{\infty}∞∞ 型未定式时,可通过导数将问题转化为:
limf(x)g(x)=limf′(x)g′(x). \lim \frac{f(x)}{g(x)}=\lim \frac{f'(x)}{g'(x)}. limg(x)f(x)=limg′(x)f′(x).
其理论依据正是柯西中值定理。
泰勒公式(Taylor's Formula)
泰勒公式可视为微分中值定理的精细化与高阶推广,它用多项式在局部逼近复杂函数,并通过余项精确刻画误差:
f(x)=f(x0)+f′(x0)(x−x0)+⋯+f(n)(ξ)n!(x−x0)n. f(x)=f(x_0)+f'(x_0)(x-x_0)+\cdots+\frac{f^{(n)}(\xi)}{n!}(x-x_0)^n. f(x)=f(x0)+f′(x0)(x−x0)+⋯+n!f(n)(ξ)(x−x0)n.
在数值计算、误差分析和工程建模中具有基础性作用。
!NOTE
具体的就不再进行标记,这里的泰勒级数可以展开的说一下,主要是比较特别,而且联系到了傅里叶变换以及坐标系,很多地方都用到了,包括线性空间等,甚至CRC校验里也有泰勒公式的身影。
泰勒公式不仅可以理解为线性空间,它实际上是函数空间向线性空间(向量空间)投影、分解的一种极致体现。泰勒展开就是把一个复杂的、难以捉摸的连续函数,投影到了由多项式构成的无限维线性空间中。
A. 导数(局部信息决定整体行为)
泰勒公式的核心假设是:一个函数在某一点的各阶导数,包含了该函数在附近区域的所有基因。
这是一种"窥一斑而知全豹"的能力。如果函数是"解析"的(如 sinx,ex\sin x, e^xsinx,ex),那么它在一点的信息确实可以无限延伸到整个定义域。
B. 多项式逼近定理(Weierstrass Approximation Theorem)
这是泰勒公式在函数空间里的"合法性"来源。
- 该定理证明:对于闭区间上的任何连续函数,都可以用多项式以任意精度去逼近。
- 泰勒公式给出了这种逼近的一种具体构造方法。
C. 微积分基本定理与中值定理(逻辑链条)
泰勒公式不是凭空产生的,它是通过对导数进行反复积分推导出来的:
- 一阶支撑: 拉格朗日中值定理(确保了一阶导数可以描述函数增量)。
- 二阶及以上: 通过对 f′(t)f'(t)f′(t) 在 [x0,x][x_0, x][x0,x] 上反复使用积分中值定理,最终像剥洋葱一样剥出了高阶项和余项。
已知求未知
不定积分 是已知函数的导数,反过来求原函数。
如果函数 F(x)F(x)F(x) 的导数等于 f(x)f(x)f(x),即
F′(x)=f(x), F'(x)=f(x), F′(x)=f(x),
那么称
∫f(x) dx=F(x)+C \int f(x)\,\mathrm{d}x = F(x) + C ∫f(x)dx=F(x)+C
为 f(x)f(x)f(x) 的不定积分。
其中,F(x)F(x)F(x):一个原函数
CCC:积分常数(任意常数)
为什么一定要加「+ C」
导数会丢失常数信息:
ddx(F(x)+C)=F′(x). \frac{\mathrm{d}}{\mathrm{d}x}(F(x)+C)=F'(x). dxd(F(x)+C)=F′(x).
因此所有相差一个常数的函数都有相同的导数 ;不定积分描述的不是"一个函数",而是一族函数:
{F(x)+C∣C∈R}. \{F(x)+C \mid C\in\mathbb{R}\}. {F(x)+C∣C∈R}.
导数是给出曲线在每一点的切线斜率 ;不定积分是在已知"斜率场"的情况下,恢复可能的曲线族 ;可以理解为:已知每一点怎么"走",反推"从哪儿来"。
!NOTE
不定积分 ≠ 面积
这是最容易混淆的地方:
概念 含义 不定积分 求原函数(代数对象) 定积分 求区间累积量(面积、物理量) ∫f(x) dx不是∫abf(x) dx \int f(x)\,\mathrm{d}x \quad\text{不是}\quad \int_a^b f(x)\,\mathrm{d}x ∫f(x)dx不是∫abf(x)dx
面积意义只属于定积分。
这部分感觉比较重要,着重处理
不定积分是从局部信息重构全局系统的逆向工程。
不定积分的运算本质
不定积分的所有技巧,本质都在做一件事:把表达式变形,凑成"某个函数的导数"。
例如:
∫2x dx因为(x2)′=2x \int 2x\,\mathrm{d}x \quad\text{因为}\quad ( x^2 )' = 2x ∫2xdx因为(x2)′=2x
所以:
∫2x dx=x2+C \int 2x\,\mathrm{d}x = x^2 + C ∫2xdx=x2+C
常见基本不定积分
∫xn dx=xn+1n+1+C(n≠−1) \int x^n\,\mathrm{d}x = \frac{x^{n+1}}{n+1}+C \quad (n\neq -1) ∫xndx=n+1xn+1+C(n=−1)
微分中值定理:从整体变化推出某点的导数信息
不定积分:从局部变化(导数)反推出整体函数形态
两者在逻辑上是一对互补操作:
导数 ⟺ 不定积分 \text{导数} \;\Longleftrightarrow\; \text{不定积分} 导数⟺不定积分
不定积分不是算面积,而是"对导数做逆运算,找出所有可能的原函数"。是不是还挺意外的,不定积分就是这样一个东西,找原函数,纯粹的可怜。
定于不定的世界
既然有不定积分,那就有定积分,所以呢~
我们在各种学科里面,其实用的最多的东西是定积分,在说积分的时候也是说的定积分。
定积分描述的是:
在一个确定区间内,函数值的累积效果。
设函数 f(x)f(x)f(x) 在区间 [a,b][a,b][a,b] 上可积,则
∫abf(x) dx \int_a^b f(x)\,\mathrm{d}x ∫abf(x)dx
称为 f(x)f(x)f(x) 在 [a,b][a,b][a,b] 上的定积分。
直观本质(从"加法极限"理解)
定积分的本质不是"算公式",而是一个极限过程:
- 把区间 [a,b][a,b][a,b] 分成很多小段
- 每一小段近似看成一个"长为 Δx\Delta xΔx、高为 f(xi)f(x_i)f(xi)"的矩形
- 把所有小矩形面积加起来
- 让分段无限细(Δx→0\Delta x \to 0Δx→0)
数学表达为:
$$
\int_a^b f(x),\mathrm{d}x
\lim_{n\to\infty}
\sum_{i=1}^n f(x_i),\Delta x
**定积分** **=** **连续量的极限求和** #### **几何意义(但不止是面积)** 当 f(x)≥0f(x)\\ge 0f(x)≥0:定积分等于曲线与 xxx 轴之间的**面积** 当 f(x)f(x)f(x) 有正有负:定积分等于**代数面积**(正负抵消) 注意: > **定积分本质是"累积量",面积只是其中一种解释。** 定积分在物理中极其自然: | 被积函数 | 定积分意义 | |----------------|-------| | 速度v(t)v(t)v(t) | 位移 | | 电流i(t)i(t)i(t) | 电荷 | | 功率p(t)p(t)p(t) | 能量 | | 概率密度 | 概率 | 统一理解为: 总量=∫"密度"×"尺度" \\text{总量} = \\int \\text{"密度"} \\times \\text{"尺度"} 总量=∫"密度"×"尺度" > \[!NOTE\] > > 这部分解释的,有点茅塞顿开的感觉,但是吧,道理到处都有,还是要仔细的品。剑来里有这么个意思,最好的道理都是在几块钱的书本上,这样才能让众人学习,知识本身就是廉价的,越廉价越好,但是要反复的去琢磨,才能够明白。有事没事多看看。 > > 不定积分是"因",定积分是"果";不定积分是"过程",定积分是"状态的改变量"。 > > #### **微积分基本定理(核心桥梁)** 我们看出来了,定积分就是累积,但是呢,计算方式只有切片,累积,求极限,真踏马咋算啊。 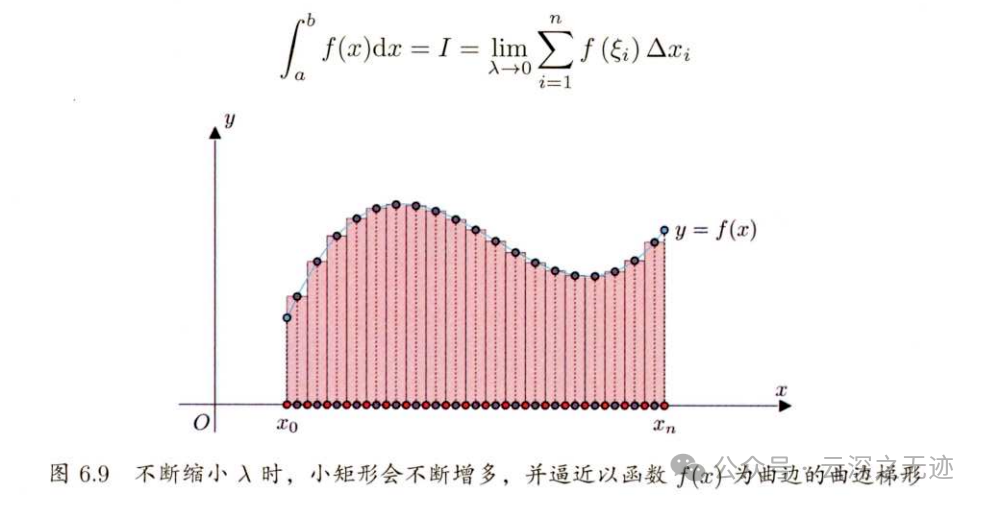 > **定积分可以通过原函数来计算。** 若 F′(x)=f(x)F'(x)=f(x)F′(x)=f(x),则: ∫abf(x) dx=F(b)−F(a) \\int_a\^b f(x)\\,\\mathrm{d}x= F(b)-F(a) ∫abf(x)dx=F(b)−F(a) 这一定理把:**极限求和(定积分定义)** 和 **导数的逆运算(不定积分)** 严密地连接在一起。 #### **为什么"上下限一减,常数就没了"** 因为: (F(x)+C)∣ab=(F(b)+C)−(F(a)+C)=F(b)−F(a) (F(x)+C)\\Big\|_a\^b= (F(b)+C)-(F(a)+C)= F(b)-F(a) (F(x)+C) ab=(F(b)+C)−(F(a)+C)=F(b)−F(a) 这就是为什么:不定积分一定要加 +C+C+C,定积分结果却**不含常数** #### **重要性质(工程/数学都常用)** **区间可加性** ∫abf(x) dx=∫acf(x) dx+∫cbf(x) dx \\int_a\^b f(x)\\,\\mathrm{d}x= \\int_a\^c f(x)\\,\\mathrm{d}x + \\int_c\^b f(x)\\,\\mathrm{d}x ∫abf(x)dx=∫acf(x)dx+∫cbf(x)dx **线性性** ∫ab(αf+βg) dx=α∫abf dx+β∫abg dx \\int_a\^b (\\alpha f+\\beta g)\\,\\mathrm{d}x= \\alpha\\int_a\^b f\\,\\mathrm{d}x + \\beta\\int_a\^b g\\,\\mathrm{d}x ∫ab(αf+βg)dx=α∫abfdx+β∫abgdx **区间反向变号** ∫baf(x) dx=−∫abf(x) dx \\int_b\^a f(x)\\,\\mathrm{d}x= -\\int_a\^b f(x)\\,\\mathrm{d}x ∫baf(x)dx=−∫abf(x)dx 导数:**局部变化率,** 定积分:**局部变化率的全局累积** 结合中值定理,可以得到: > 在某一点,瞬时值等于整体平均效果 这正是物理与工程中"等效""平均"的数学基础。 定积分不是算面积,而是"对连续变化进行极限求和,得到一个确定的总量"。 定积分把无数个离散的、局部的"瞬时变化",通过无穷求和的方式,"缝合"成了一个宏观的"跨度"。 ### **从"信号"开始:你到底在积分什么?** 在工程里,**信号不是函数,是"物理量随时间变化"** : 电压信号:v(t)v(t)v(t)(V) 电流信号:i(t)i(t)i(t)(A) 速度信号:v(t)v(t)v(t)(m/s) 加速度信号:a(t)a(t)a(t)(m/s²) **关键信息**: > 信号本身往往不是我们最终关心的量,而是"变化率"或"密度"。 ### **第一层积分:信号 → 累积量(物理)** #### **速度 → 位移** x(t)=∫v(t) dt x(t)=\\int v(t)\\,\\mathrm{d}t x(t)=∫v(t)dt v(t)v(t)v(t):瞬时变化率 积分结果:**真实走过的路程** > 积分 = 把"瞬时贡献"累加成"总效果" #### **电流 → 电荷** Q=∫i(t) dt Q=\\int i(t)\\,\\mathrm{d}t Q=∫i(t)dt 电流是"电荷流动速率",积分给出"流过了多少电荷"。 #### **功率 → 能量(最重要)** E=∫p(t) dt E=\\int p(t)\\,\\mathrm{d}t E=∫p(t)dt 功率是"能量变化率",能量才是系统真正消耗/存储的东西 **第一层结论**: > **定积分在工程中** **=** **对"密度 / 变化率"的时间累积** 在这多想一句,都是对时间的积分,主要是在时间域上。 ### **第二层:信号平方 → 能量** #### **电信号的能量从哪来?** 电阻上的瞬时功率: p(t)=v2(t)R p(t)=\\frac{v\^2(t)}{R} p(t)=Rv2(t) 于是能量: E=∫v2(t)R dt E=\\int \\frac{v\^2(t)}{R}\\,\\mathrm{d}t E=∫Rv2(t)dt 忽略常数 1/R1/R1/R,工程上定义: E∝∫v2(t) dt \\boxed{E \\propto \\int v\^2(t)\\,\\mathrm{d}t} E∝∫v2(t)dt #### **为什么是平方,而不是绝对值?** 正负电压 **都在消耗能量**,线性积分会正负抵消 ;平方积分保证:能量 ≥ 0,与物理功耗一致,这一步直接导致了:RMS,功率谱密度(PSD),噪声分析,信噪比(SNR)。 ### **第三层:有限时间 → 平均 → RMS** 工程里你**永远不可能积分到无穷** ,于是引入时间窗 TTT。 #### **平均功率** Pavg=1T∫0Tv2(t) dt P_{\\text{avg}}= \\frac{1}{T}\\int_0\^T v\^2(t)\\,\\mathrm{d}t Pavg=T1∫0Tv2(t)dt #### **RMS 的真正定义** vRMS=1T∫0Tv2(t) dt v_{\\text{RMS}}= \\sqrt{ \\frac{1}{T}\\int_0\^T v\^2(t)\\,\\mathrm{d}t } vRMS=T1∫0Tv2(t)dt 这不是"定义出来的",而是**功率反推出来的**。 > RMS 是"等效直流功率"的数学形式积分是为了能量,平均是为了稳态 ### **第四层:频域视角(Parseval 等价)** 工程师不总在时域干活。 #### **时域能量** E=∫∣x(t)∣2 dt E=\\int \|x(t)\|\^2\\,\\mathrm{d}t E=∫∣x(t)∣2dt #### **频域等价** E=∫∣X(f)∣2 df E=\\int \|X(f)\|\^2\\,\\mathrm{d}f E=∫∣X(f)∣2df 这不是巧合,是 Parseval 定理 > \[!NOTE\] > > 在信号处理和数学分析中,**帕塞瓦尔定理** (Parseval's Identity/Theorem),也常被称为**能量等价原理** ,是连接**时域(或空域)与频域**的桥梁。 > > 简单来说,它的核心意义是:**信号在时域的总能量,等于它在频域的总能量。** --- > > 数学表达式 > > 对于一个能量有限的连续信号 f(t)f(t)f(t),其傅里叶变换为 F(ω)F(\\omega)F(ω),等价关系表达为: > > ∫−∞∞∣f(t)∣2dt=12π∫−∞∞∣F(ω)∣2dω \\int_{-\\infty}\^{\\infty} \|f(t)\|\^2 dt = \\frac{1}{2\\pi} \\int_{-\\infty}\^{\\infty} \|F(\\omega)\|\^2 d\\omega ∫−∞∞∣f(t)∣2dt=2π1∫−∞∞∣F(ω)∣2dω > > * **左侧:** 信号在时域内对**平方**的积分,代表总能量。 > * **右侧:** 信号在频域内对**功率谱密度**的积分,同样代表总能量。 > > > **注意:** 系数(如 12π\\frac{1}{2\\pi}2π1)取决于你使用的傅里叶变换定义(角频率 ω\\omegaω 还是频率 fff)。如果是离散傅里叶变换(DFT),则表现为序列平方和的等价。 #### **工程结论** 噪声能量 = PSD × 带宽,滤波器改变能量 = 改变积分范围,ENBW 本质 = **等效积分宽度** ### **把"定积分"放进工程统一框架** 现在我们可以可以把所有东西放进一张表: | 场景 | 被积函数 | 积分意义 | |--------|-------------------|------| | 速度 | v(t)v(t)v(t) | 位移 | | 电流 | i(t)i(t)i(t) | 电荷 | | 功率 | p(t)p(t)p(t) | 能量 | | 信号 | x2(t)x\^2(t)x2(t) | 信号能量 | | 噪声 PSD | S(f)S(f)S(f) | 噪声功率 | **定积分在工程中的真正身份** : **"连续能量 / 物理量守恒的计算工具"** 。 在工程里,定积分不是数学工具,而是"能量守恒的计算语言"。**信号 → 平方 → 积分 → 能量 → 性能指标** 如果上面是工程的故事,那下面就是哲学的世界,**为什么在自然、物理、测量、信号与系统里,积分几乎不可替代**这个角度,给一个体系化的答案。 > 积分之所以有用,是因为:世界中"有意义的量",几乎都不是瞬时值,而是"在时间或频率上的累积效应"。 积分不是一种数学技巧,而是**描述"累积、记忆、平均、能量、概率"的唯一一致语言**。 ### **为什么"瞬时值"在真实系统里几乎没有意义?** ### **瞬时值是理想化的、人造的概念** 在数学里x(t0)x(t_0)x(t0) 是一个点,可以被精确讨论;但在现实系统中:没有无限带宽,没有零噪声,没有零时间分辨率;所以:任何真实系统,都无法"看到一个点",它只能看到"一段时间的影响"。 ### **所以"测量"必然等价于积分** 无论你承认与否,任何测量都等价于: y=∫x(t) w(t) dt y = \\int x(t)\\,w(t)\\,dt y=∫x(t)w(t)dt 只是你可能叫它:平均,滤波,累加,相关,能量计算;但数学上,它们**全是积分**。 ### **积分 = "记忆"的数学形式** ### **没有积分,就没有"系统"** 一个系统的根本特征是:**它会记住过去对现在的影响** ;数学上,"记住过去"只有一种办法: **把过去的值加进来**,这就是积分。 RC 电路: V(t)=1RC∫−∞tx(τ)e−(t−τ)/RCdτ V(t)=\\frac{1}{RC}\\int_{-\\infty}\^t x(\\tau)e\^{-(t-\\tau)/RC}d\\tau V(t)=RC1∫−∞tx(τ)e−(t−τ)/RCdτ FIR 滤波器: y\[n\]=∑kx\[n−k\]h\[k\] y\[n\]=\\sum_k x\[n-k\]h\[k\] y\[n\]=k∑x\[n−k\]h\[k\] 平均值: xˉ=1T∫0Tx(t) dt \\bar{x}=\\frac{1}{T}\\int_0\^T x(t)\\,dt xˉ=T1∫0Tx(t)dt > **系统** **=** **积分器 + 权重函数** ### **积分是"从微观到宏观"的唯一桥梁** ### **微观噪声是不可预测的,只能"统计"** 噪声在微观层面是:随机,不可预测,瞬时值毫无意义 唯一能做的是: > **把它们"加起来",看整体效应** 这在数学上只能通过积分实现。 ### **为什么 RMS、功率、能量都离不开积分** 能量: E=∫∣x(t)∣2dt E=\\int \|x(t)\|\^2 dt E=∫∣x(t)∣2dt 功率谱: σ2=∫S(f)∣H(f)∣2df \\sigma\^2=\\int S(f)\|H(f)\|\^2 df σ2=∫S(f)∣H(f)∣2df Allan variance:本质也是对 PSD 的加权积分 > **所有"稳定的、可比较的物理量",都是积分量** > \[!NOTE\] > **阿伦方差** (Allan Variance, AVAR),又称**双样本方差** ,是表征时钟、振荡器以及各类传感器(如你关注的雷达系统中的晶振或陀螺仪)**频率稳定度**的一种时域测量指标。 > > 与计算所有数据平均值的传统方差不同,阿伦方差关注的是**相邻两个采样段平均值之间的差异**。 > > 若有一组频率偏离数据,将其分成时长为 τ\\tauτ 的若干段,其数学表达式为: > > σy2(τ)=12(M−1)∑i=1M−1(yˉi+1−yˉi)2 \\sigma_y\^2(\\tau) = \\frac{1}{2(M-1)} \\sum_{i=1}\^{M-1} (\\bar{y}_{i+1} - \\bar{y}_i)\^2 σy2(τ)=2(M−1)1i=1∑M−1(yˉi+1−yˉi)2 > > * \*\*τ\\tauτ\*\* **(相关时间/平滑时间)** :这是阿伦方差的自变量。改变 τ\\tauτ 的大小,可以分析不同时间尺度下的稳定性。 > * **yˉi\\bar{y}_iyˉi** :第 iii 个时间段内的平均频率。 > * **物理意义** :它测量的是系统在间隔为 τ\\tauτ 的两次测量之间,频率发生"漂移"或"波动"的程度。 ### **积分天然"****压制无结构,保留有结构** **"** 这是积分最"神奇"、也是最核心的能力。 ### **为什么积分能"消噪"?** 考虑两类信号: **随机的**:正负交替、无结构 **有结构的**:同相、同频、相关 积分对它们的作用完全不同: 随机项: ∫n(t) dt→增长慢 / 相互抵消 \\int n(t)\\,dt \\to \\text{增长慢 / 相互抵消} ∫n(t)dt→增长慢 / 相互抵消 相干项: ∫Acos(ωt)cos(ωt) dt→线性累加 \\int A\\cos(\\omega t)\\cos(\\omega t)\\,dt \\to \\text{线性累加} ∫Acos(ωt)cos(ωt)dt→线性累加 > **积分是"相关性的放大器,不相关性的湮灭器"** (我好喜欢湮灭这个词啊) 这不是技巧,这是**数学必然性**。 ### **积分是"尺度变换"的工具** ### **积分把"细节"变成"尺度"** 当做积分时,在说一句非常物理的话: > "我不关心微小起伏,我关心整体趋势" 这意味着:积分 = 放弃高频细节,积分 = 选择一个时间/频率尺度。 ### **这就是为什么积分天然连接到带宽、ENBW、τ** 积分时间 ↑→ 有效带宽 ↓→ 噪声 ↓→ 响应慢,这是任何测量系统**绕不开的尺度权衡**。 ### **积分是唯一"坐标无关"的操作** 这是一个非常深的数学事实。 ### **积分在变换下仍然成立** 换坐标,等效为换表示(时域 ↔ 频域),换基函数也是如此;**积分的物理意义不变**。这也是为什么:Parseval 定理,能量守恒,PSD 积分在不同表象下仍然一致。 > **积分是"表象无关"的量** ### **为什么信号链里"越走越离不开积分"?** 现在把话说得非常直接:我们关心的是噪声底,稳定性,分辨率,长期行为,可重复性,而这些东西**没有一个是瞬时的**。 它们本质上全是: > **某种积分意义下的统计量** 所以会自然发现:ENBW 是积分定义,Allan variance 是积分定义,Lock-in 是积分实现,滤波是积分实现,平均是积分实现。 ## **底层原因** 如果只允许一句话解释"为什么积分这么有用",那就是:自然界的噪声是局部的,而我们关心的物理量是整体的;积分是从"局部不确定"通向"整体确定"的唯一道路。 在真实系统中,瞬时值既不可观测,也不可重复。所有有意义的测量,都是对随机过程在某个尺度上的累积响应。积分之所以无处不在,不是因为数学家喜欢它,而是因为这是唯一能把随机性压缩成稳定数量的数学结构。 不定积分不是算面积,而是"对导数做逆运算,找出所有可能的原函数"。