数据结构二叉树—堆(2)&链式结构(上)

我们接着上一章节将起

获取前k个最小数

既然要获取前k个最小数，当我们前K个数一定是排好顺序的要么升序要么降序

int data[] = { 4,2,8,1,5,6,9,3 };
HP hp;
HPInit(&hp);
for (int i = 0; i < sizeof(data) / sizeof(data[0]); i++)
{
	HPPush(&hp, data[i]);
}
int k = 0;
scanf("%d", &k);
while (k--)
{
	printf("%d ", HPTop(&hp));
	HPPop(&hp);
}
HPDestroy(&hp);

如果我要找到前K个最大的数那么我们就只需要把小堆换成大堆即可

堆的空间复杂度

void TestHeap1()
{
	int data[] = { 4,2,8,1,5,6,9,3 };
	HP hp;
	HPInit(&hp);
	for (int i = 0; i < sizeof(data) / sizeof(data[0]); i++)
	{
		HPPush(&hp, data[i]);
	}
	int i = 0;
	while (!HPEmpty(&hp))
	{
		printf("%d ", HPTop(&hp));
		//data[i++] = HPTop(&hp);
		HPPop(&hp);
	}
	
	HPDestroy(&hp);
}

我们知道这串代码的输出结果就是一个升序的结果原因是小堆进行获取堆顶数据和堆删除的代码得到的就是最小的数据但是我们会发现由于我们创建了一个堆进行存放数组数据就会导致该代码的空间复杂度为O(N)=N ,那为什么是N呢？空间复杂度核心是看程序运行过程中占用的额外空间与输入规模N的关系，统计程序运行期间额外占用的临时空间或者动态空间不包含输入本身占用的空间，额外空间主要来自于堆结构HP的动态内存分配， 在执行循环到时候会将N个元素依次存入堆的动态空间中堆的动态空间大小会**随着N的增加而线性增加，**后续只是弹出堆顶元素调整堆结构不会释放堆的核心动态空间所以在运行期间始终能容纳n个元素的额外空间后续只是弹出堆顶元素调整堆结构不会释放堆的核心动态空间所以在运行期间始终能容纳N个元素的额外空间

堆排序的时间复杂度

堆排序的时间复杂度同程来说是**O(N*logN)**且是稳定高效排序

堆排序核心分成两步

• 把数组建立成大顶堆或者小顶堆
• 循环取堆顶交换末尾向下调整完成排序

建堆

从最后一个非叶子节点向前逐个向下调整总操作次数远小于O(N*logN)，为O(N)

排序主体

一共执行N减一次弹出或者交换操作每次向下调整堆的高度是log2^N的对数

所以最终的时间复杂度为O(N*logN)

TopK问题

这个问题其实就是在一堆数据中获取前K个最大的数或者最小的数 ，在上面我们已经讲解了获取前K个最小的数，逻辑上就是先建立一个空堆， 将数组每个数据存放在空堆中利用向上调整算法进行建堆然后获取堆顶数据再进行堆的删除， 这个操作我要循环进行K次可以获取到前K个最大或最小数但是还有一个问题，虽然数据在存放磁盘文件中的而磁盘文件相较于内存是非常大的所以不需要担心数据过多的情况但是我们知道创建的堆是存放在电脑的内存中，如果有一个例子总共有一百万个整型类型的数据要从中获取前十个最大的值如果按照上面的方法我们就需要创建一个堆来存放知识一百万个数据将这一百万个数据转化成内存的大小那将会是非常消耗内存空间的，所以一般**如果总数据个数不大的情况下直接堆排序就可以解决问题，**这就是我们今天要讲的例子，利用极小的内存空间就能解决top K问题

• 我们要先建立一个堆 ，但是不同于上面把所有数据都存放在堆中，我们只需要取前K个数据进行建堆 如果是获取前K个最大的数则建立小堆 如果获取前K个最小的数则建立大堆
• 再利用剩下的N-K个元素依次与堆顶元素来比较如果大于堆顶元素就替换堆顶元素
• 替换完之后再利用向下调整算法重新计算小堆将上述操作循环执行N-K次

原理其实很简单这其实就是利用了小堆一个性质：堆顶数据在当前堆中是最小的，也就是说我们要获取前K个最大值则建立小堆，用剩余数据依次和堆顶数据比较如果大于堆顶数据则替换堆顶元素，再用向下调整算法重新变成小堆，此时堆顶数据就是第二小的以此类推我们就可以把所有较小数据进行覆盖到最后只留下前K个最大值也就是堆中数据但需要注意的是这K个数并不一定是有序的，只是获取到了前K个最大值

void CreateNData()
{
	//造数据
	int n = 100000;
	srand(time(0));
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen");
		return;
	}
	for (int i = 0; i < n; ++i)
	{
		int x = (rand() + i) % 1000000;
		fprintf(fin, "%d\n", x);
	}
	fclose(fin);
}

写代码之前一定你要先创建一个"data.txt"的文本文档

void TestHeap3()
{
	int k;
	printf("请输入k>");
	scanf("%d", &k);
	int* kminheap = (int*)malloc(sizeof(int) * k);
	if (kminheap == NULL)
	{
		perror("kminheap");
		return;
	}
	const char* file = "data.txt";
	FILE* fin = fopen(file, "r");
	if (fin == NULL)
	{
		perror("fopen");
		return;
	}
	//读取文件中的前k个数
	for (int i = 0; i < k; i++)
	{
		int x = rand() + i;
		fscanf(fin,"%d", &kminheap[i]);
	}
	//用k个数建一个小堆
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(kminheap, k, i);
	}
	//读取剩下的n-k个数
	int x = 0;
	while (fscanf(fin,"%d", &x)>0)
	{
		if (x > kminheap[0])
		{
			kminheap[0] = x;
			AdjustDown(kminheap, k, 0);
		}
	}
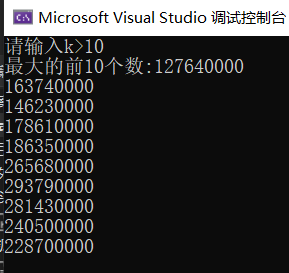
	printf("最大的前%d个数:",k);
	for (int i = 0; i < k; i++)
	{
		printf("%d ", kminheap[i]);
	}
	printf("\n");
}

链表实现二叉树结构

用链表来表示一颗二叉树，用链来指示元素的逻辑关系，通常的方法是链表中每个结点由三个域组成，数据域和左右指针域左右指针域分别给出该节点左子树和右子树所在的链接点的存储地址

#include<stdio.h>
#include<stdlib.h>
typedef int HPDataType;
typedef struct Binaty_tree
{
	HPDataType* data;
	struct Binaty_tree* left;
	struct Binaty_tree* right;
}BTNode;

手动创建二叉树

我们手动创建二叉树其实就是给二叉树的每一个结点开辟一块空间然后用左右指针进行连接

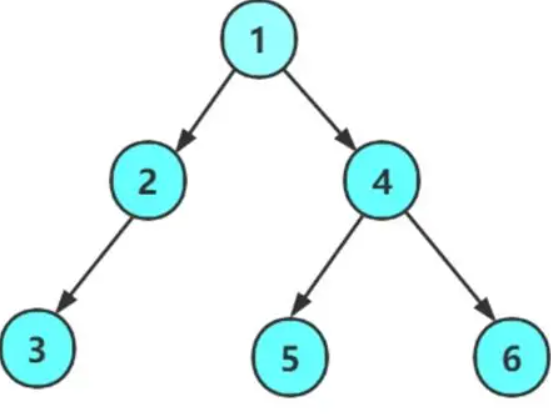
BTNode* BuyNode(int x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc");
		return NULL;
	}
	node->data = x;
	node->left = node->right = NULL;
}
BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
	node6->right = node7;
	return node1;
}
void Test1()
{
    BTNode* root = CreatBinaryTree();
}
int main()
{
    Test1();
}

现在我们已经创建好了二叉树结构

前序遍历

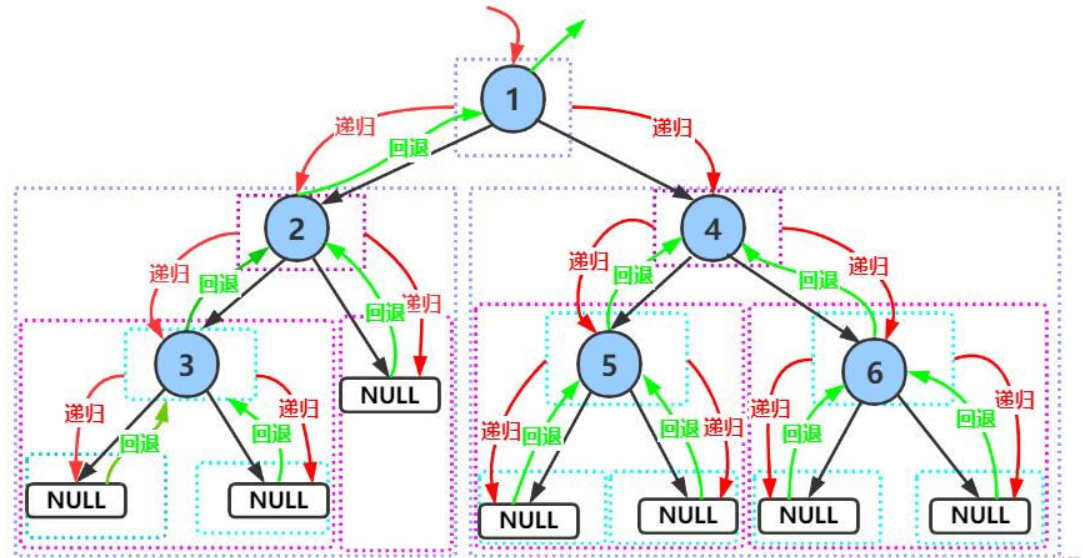
前序遍历访问根节点的操作发生在遍历其左右子树之前

访问顺序：根节点，左子树，右子树

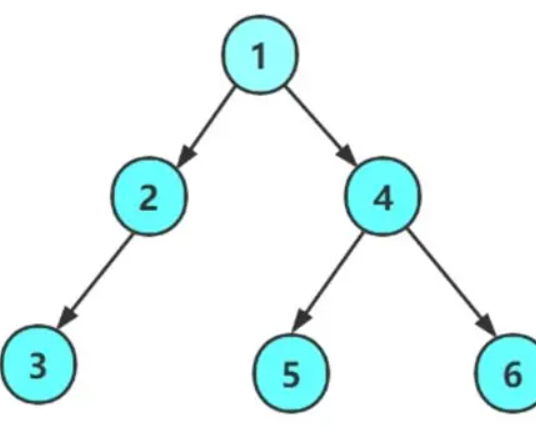
我们用这幅图为例，用N表示空

前：1->2->3->N->N->N->4->5->N->N->6->N->N

void PrevOrder(BTNode* root)//前序遍历
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

中序遍历

中序遍历访问根结点操作发生在遍历其左右子树中间

访问顺序：左子树，根节点，右子树

中：N->3->N->2->N->1->N->5->N->4->N->6->N

void InOrder(BTNode* root)//中序遍历
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

后序遍历

后序遍历就是访问根节点在左右节点之后

访问顺序：左子树，右子树，根节点

后：N->N->3->N->2->N->N->5->N->6->4->1

void EndOrder(BTNode* root)//后序遍历
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	EndOrder(root->left);
	EndOrder(root->right);
	printf("%d ", root->data);
}