目录
-
- 一、引言
- 二、熵力
- 三、牛顿定律的涌现
-
- [3.1 力与惯性](#3.1 力与惯性)
- [3.2 牛顿万有引力定律](#3.2 牛顿万有引力定律)
- [3.3 推导的自然性与稳健性](#3.3 推导的自然性与稳健性)
- [3.4 惯性与牛顿势](#3.4 惯性与牛顿势)
- 四、一般物质分布的涌现引力
-
- [4.1 一般物质分布的泊松方程](#4.1 一般物质分布的泊松方程)
- [4.2 任意粒子位置的引力](#4.2 任意粒子位置的引力)
- 五、等效原理与爱因斯坦方程
-
- [5.1 惯性定律与等效原理](#5.1 惯性定律与等效原理)
- [5.2 爱因斯坦方程的推导](#5.2 爱因斯坦方程的推导)
- [5.3 任意位置粒子集合受到的力](#5.3 任意位置粒子集合受到的力)
- 六、结论与讨论
-
- [6.1 引力作为基本力的终结](#6.1 引力作为基本力的终结)
- [6.2 对弦理论的影响及与AdS/CFT的关系](#6.2 对弦理论的影响及与AdS/CFT的关系)
- [6.3 重新审视黑洞视界](#6.3 重新审视黑洞视界)
- [6.4 最终讨论](#6.4 最终讨论)
- 致谢
- 参考文献
埃里克·韦尔林德------阿姆斯特丹大学理论物理研究所,荷兰阿姆斯特丹,瓦尔肯尼尔大街65号,1018 XE
摘要 :基于基本原理和普适假设,本文表明:在时空通过全息图景涌现的理论中,牛顿万有引力定律会自然且不可避免地出现。引力被解释为熵力------由物质体位置相关的信息变化所引发。对上述论证进行相对论推广,可直接导出爱因斯坦方程。当空间是涌现的时,即便是牛顿惯性定律也需要被解释。等效原理使我们得出结论:惯性定律的起源实际上也是熵性的。
一、引言
在自然界的所有力中,引力无疑是最普适的。它影响所有携带能量的事物,且与时空结构密切相关。引力的普适性还体现在其基本方程与热力学和流体力学定律高度相似 [ 2 ] ^{[2]} [2]------但迄今为止,这种相似性尚未有明确的解释。
引力在大尺度上占主导地位,但在小尺度上极其微弱。事实上,其基本定律仅在毫米量级的距离上得到验证。与其他所有力相比,引力与量子力学的融合也困难得多。因此,在微观层面上将引力与其他自然力统一的探索或许并非正确路径------这一方向已导致诸多问题、悖论和谜题。弦理论在一定程度上解决了其中部分问题,但并非全部;我们仍需厘清弦理论解决方案所蕴含的深层意义。
许多物理学家认为,引力和时空几何是涌现现象。弦理论及其相关进展也提供了诸多相关线索,其中尤为重要的启示来自AdS/CFT对偶(或更一般地,开弦/闭弦对偶)。这种对偶性揭示了含引力理论与不含引力理论之间的等价关系,为"引力可从不含引力的微观描述中涌现"提供了证据。
引力的普适性表明,其涌现应基于独立于底层微观理论具体细节的普适原理。本文将论证:推导引力的核心概念是信息------更准确地说,是与物质及其位置相关的信息量(无论微观理论以何种形式呈现,均以熵为度量)。当物质发生位移时,熵的变化会产生熵力,而这种熵力正是引力的表现形式。因此,引力的起源在于微观理论趋向于最大化其熵的统计趋势。
本文最核心的假设是:与空间某一部分相关的信息遵循全息原理 [ 8 , 9 ] ^{[8,9]} [8,9]。全息原理最有力的支持证据来自黑洞物理 [ 1 , 3 ] ^{[1,3]} [1,3]和AdS/CFT对偶 [ 10 ] ^{[10]} [10]。这些理论进展表明,至少部分微观自由度可以全息地表示在时空边界或视界上。
然而,全息概念的适用范围似乎更为广泛。例如,在AdS/CFT对偶中,可通过全息版重整化群将边界向内移动;类似地,黑洞物理中存在"信息可存储在拉伸视界上"的观点;此外,通过考虑加速观测者,原则上可在空间中任意位置定位全息屏幕。在所有这些情形中,全息方向的涌现都伴随着红移,且与某种粗粒化过程相关。如果这些观点的组合是正确的,那么应当存在一个普适框架,描述空间如何与引力一同涌现。
通常,全息原理的研究局限于相对论背景,但引力同样存在于我们日常的非相对论世界中。无论引力的起源是什么,它都应自然解释为何这种力会以当前的形式存在,并遵循牛顿万有引力定律。事实上,当空间是涌现的时,牛顿的其他定律也必须被重新推导------因为位置、速度、加速度、质量和力等标准概念并非显而易见。在这种情况下,力学定律必须与空间本身一同涌现。即便是惯性这样的基本概念,也并非既定事实,需要重新解释。
本文提出了一个空间涌现的全息图景,并探讨了引力和惯性的起源------二者通过等效原理相互关联。仅基于能量、熵和温度等与空间无关的概念,从基本原理出发,本文表明牛顿定律会自然且几乎不可避免地出现。引力被解释为熵力,其根源是与物质体位置相关的信息量变化。
一个关键要素是:由全息原理决定,给定空间体积仅关联有限数量的自由度。与物质等效的能量均匀分布在这些自由度上,从而产生温度。本文将证明:温度与物质位移引发的熵变的乘积,等于引力所做的功------牛顿万有引力定律以令人惊讶的简单方式涌现。
全息原理并非易从牛顿定律和爱因斯坦方程中提炼,它深深隐藏于这些定律之中。相反,从全息原理出发,我们发现这些熟知的定律可直接且不可避免地推导得出。通过逆转人们从引力定律到全息原理的逻辑,我们将获得关于引力本质的更清晰、更简洁的图景------例如,它阐明了为何引力在没有中间媒介场的情况下仍能实现超距作用。
本文提出的观点与弦理论的现有知识一致,但如果正确,它们也将对弦理论产生重要影响。特别是,"引力源于闭弦交换"的描述将不再成立------事实上,弦本身似乎也必须是涌现的。
本文结构如下:第二节阐述熵力的概念;第三节在简单的非相对论背景下展示核心启发性论证;第四节将其推广到任意物质分布;第五节将结果拓展到相对论情形,并推导爱因斯坦方程;第七节给出结论。
二、熵力
熵力是一种宏观有效力,起源于具有多自由度的系统通过统计趋势增加其熵的过程。熵力方程由熵差表示,与微观动力学的细节无关------特别地,熵力没有对应的基本场。熵力通常出现在宏观系统中(如胶体物理或生物物理领域)。例如,悬浮在更小粒子热环境中的大胶体分子,会因排阻体积效应而受到熵力;渗透现象是另一种由熵力驱动的过程。
最著名的例子或许是聚合物分子的弹性。单个聚合物分子可建模为由许多固定长度的单体连接而成,每个单体可围绕连接点自由旋转并指向任意空间方向------所有这些构型具有相同的能量。当聚合物分子浸入热浴时,它倾向于处于随机卷曲构型(因为这些构型在熵上更有利):与拉伸成直线的构型相比,卷曲构型的数量要多得多。这种回归最大熵状态的统计趋势,转化为宏观的弹性力。
如图1所示,可用镊子将聚合物的两端拉开,通过外力 F F F使其偏离平衡构型。为明确起见,我们固定一端(例如在原点),并将另一端沿x轴移动。熵的表达式为:
S ( E , x ) = k B log Ω ( E , x ) (2.1) S(E,x)=k_{B}\log \Omega (E,x) \tag{2.1} S(E,x)=kBlogΩ(E,x)(2.1)
其中 k B k_{B} kB是玻尔兹曼常数, Ω ( E , x ) \Omega(E, x) Ω(E,x)表示整个系统的构型空间体积(作为热浴总能量 E E E和第二端点位置 x x x的函数)。 x x x的依赖性完全是构型效应:能量 E E E中没有依赖于 x x x的微观贡献。
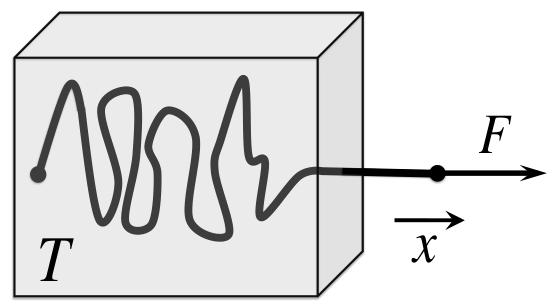
图1:自由连接的聚合物浸入温度为 T T T的热浴中,并被外力 F F F拉出平衡态。熵力指向相反方向。
在正则系综中,力 F F F作为与聚合物长度 x x x对偶的外变量,被引入配分函数 [ 3 ] ^{[3]} [3]:
Z ( T , F ) = ∫ d E d x Ω ( E , x ) e − ( E + F x ) / k B T (2.2) Z(T, F)=\int d E d x \Omega(E, x) e^{-(E+F x) / k_{B} T} \tag{2.2} Z(T,F)=∫dEdxΩ(E,x)e−(E+Fx)/kBT(2.2)
在给定温度 T T T下,使聚合物保持固定长度 x x x所需的力 F F F,可由鞍点方程推导得出:
1 T = ∂ S ∂ E , F T = ∂ S ∂ x (2.3) \frac{1}{T}=\frac{\partial S}{\partial E}, \quad \frac{F}{T}=\frac{\partial S}{\partial x} \tag{2.3} T1=∂E∂S,TF=∂x∂S(2.3)
通过力的平衡,外力 F F F应等于试图将聚合物恢复到平衡位置的熵力。熵力的特征的是:(1)指向熵增加的方向;(2)与温度成正比。对于聚合物,其受力遵循胡克定律:
F 聚合物 ∼ − 常数 ⋅ k B T ⟨ x ⟩ (2.4) F_{\text{聚合物}} \sim- \text{常数} \cdot k_{B} T \langle x \rangle \tag{2.4} F聚合物∼−常数⋅kBT⟨x⟩(2.4)
这个例子表明,在宏观层面上,熵力可以是保守力(至少在温度恒定的情况下)。然而,相应的势能没有微观意义,是涌现的。
值得研究的是:当聚合物逐渐回到平衡位置、力对外部系统做功时的能量和熵平衡。根据能量守恒,这些功必须等于从热浴中提取的能量------因此热浴的熵会减少。对于无限大的热浴,热浴熵的减少量与聚合物熵的增加量相等,总熵保持不变。
这一过程可在微正则系综中进行更详细的研究(微正则系综考虑包括热浴在内的总能量)。为确定熵力,需再次引入外力 F F F并考察力的平衡------具体而言,考虑由 Ω ( E + F x , x ) \Omega(E+F x, x) Ω(E+Fx,x)描述的微正则系综,并要求熵取极值:
d d x S ( E + F x , x ) = 0 (2.5) \frac{d}{d x} S(E+F x, x)=0 \tag{2.5} dxdS(E+Fx,x)=0(2.5)
容易验证,这将导出与式(2.3)相同的方程。但这表明,在微正则系综中,温度通常依赖于位置,而力也依赖于能量。项 F x F x Fx可视为将聚合物拉出平衡位置时输入系统的能量。因此,该方程表明:当聚合物被缓慢允许回到平衡位置时,总能量会减少,但熵在一级近似下保持不变。
后续章节的目标是论证:引力也是一种熵力,上述推理仅需稍作修改即可适用于引力。
三、牛顿定律的涌现
空间首先是为描述粒子位置和运动而引入的工具------因此,空间本质上只是信息的"存储载体"。这些信息自然与物质相关联。由于空间每一部分允许的最大信息量是有限的,因此无法在连续空间的某一点上以无限精度定位粒子。事实上,点和坐标都是衍生概念。人们可能会假设信息存储在离散空间的点上(如格点模型),但如果所有相关信息都无冗余,就无法获得全息描述------更无法恢复引力。
因此,我们假设信息存储在曲面(或屏幕) 上。屏幕分隔不同区域,是存储"从一侧移动到另一侧的粒子"相关信息的自然场所。我们可以想象:粒子位置的信息以离散比特的形式存储在屏幕上。每个屏幕上的动力学由一些未知规则支配,这些规则可视为处理存储在屏幕上信息的方式------因此,它不必由局域场论或任何已知理论描述,微观细节与我们的研究无关。
我们还假设,与AdS/CFT对偶类似,存在一个特殊方向,对应微观理论的尺度或粗粒化变量------这正是空间涌现的方向。因此,存储信息的屏幕类似于"拉伸视界":一侧是已涌现的空间,另一侧则尚未形成空间。我们假设微观理论具有明确的时间概念,且其动力学具有时间平移不变性------这使得能量的定义成为可能,并通过统计物理技术可进一步定义温度。这些(能量、温度、熵)将作为基本要素,与信息相关联。
3.1 力与惯性
我们的起始假设直接受到贝肯斯坦原始思想实验的启发------正是该实验促使他得出了著名的熵公式。贝肯斯坦考虑了一个质量为 m m m的粒子,通过一根虚构的"绳子"被 lowering 向黑洞:在经典情况下,由于无限红移,黑洞的质量增加量可任意小。如果考虑粒子的热气体,这一事实将导致热力学第二定律的矛盾。贝肯斯坦解决了这一矛盾:当粒子距离视界约一个康普顿波长时,可认为它已成为黑洞的一部分------因此,它会使黑洞的质量和视界面积增加一个小量,而这一增量对应于一个信息比特。这一论证促使他提出了黑洞熵的面积定律。
我们希望将这一推理推广到平直非相对论空间 (而非黑洞视界附近)。考虑全息屏幕的一个小片段,以及一个质量为 m m m的粒子------该粒子从时空已涌现的一侧接近屏幕。最终,粒子会与屏幕上的微观自由度融合,但在此之前,它已会影响屏幕上存储的信息量(如图2所示)。
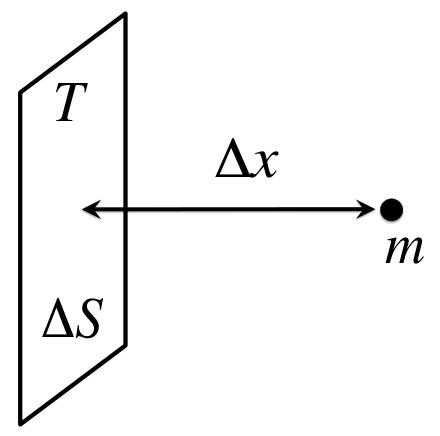
图2:质量为 m m m的粒子接近全息屏幕的一部分。屏幕界定了已涌现的空间区域(包含该粒子),并存储描述未涌现空间部分以及部分已涌现空间的信息。
受贝肯斯坦论证的启发,我们假设:与边界上信息相关的熵变满足:
Δ S = 2 π k B ( 当 Δ x = ℏ m c 时 ) (3.5) \Delta S=2 \pi k_{B} \quad (\text{当} \Delta x=\frac{\hbar}{m c} \text{时}) \tag{3.5} ΔS=2πkB(当Δx=mcℏ时)(3.5)
引入因子 2 π 2 \pi 2π的原因将很快显现。我们将该公式推广为更一般的形式,假设屏幕附近的熵变与位移 Δ x \Delta x Δx成正比:
Δ S = 2 π k B m c ℏ Δ x (3.6) \Delta S=2 \pi k_{B} \frac{m c}{\hbar} \Delta x \tag{3.6} ΔS=2πkBℏmcΔx(3.6)
为理解熵变为何也与质量 m m m成正比,可想象将粒子分裂为两个或多个更轻的子粒子------每个子粒子在位移 Δ x \Delta x Δx后都会携带各自的熵变。由于熵和质量都是可加的,因此熵变与质量成正比是自然的。
力是如何产生的?核心思想是类比半透膜上的渗透现象:当粒子因熵的原因倾向于处于膜的一侧,且膜具有温度时,粒子将受到一个有效力,满足:
F Δ x = T Δ S (3.7) F \Delta x=T \Delta S \tag{3.7} FΔx=TΔS(3.7)
这就是熵力。因此,要产生非零力,就需要非零温度。根据牛顿定律,力会导致非零加速度------而加速度与温度密切相关:正如昂鲁(Unruh)所证明的,加速参考系中的观测者会感受到一个温度 [ 5 ] ^{[5]} [5]:
k B T = 1 2 π ℏ a c (3.8) k_{B} T=\frac{1}{2 \pi} \frac{\hbar a}{c} \tag{3.8} kBT=2π1cℏa(3.8)
其中 a a a表示加速度。我们将此温度视为屏幕上比特的温度------此时,式(3.6)中 Δ S \Delta S ΔS的形式(包括因子 2 π 2 \pi 2π)的选择就变得清晰了:将式(3.8)、(3.6)和(3.7)结合,可直接恢复牛顿第二定律:
F = m a (3.9) F=m a \tag{3.9} F=ma(3.9)
式(3.8)应被解读为"产生加速度 a a a所需的温度 T T T",而非通常意义上"由加速度引起的温度"。
3.2 牛顿万有引力定律
现在假设我们的边界并非无限延伸,而是形成一个闭合曲面------更具体地说,假设它是一个球面。以下讨论中,我们可以暂时忘记昂鲁定律(3.8)(因为我们不再需要它),它仅作为式(3.6)的进一步动机。关键结论是:要产生力,就需要温度;而要理解力的起源,就需要明确温度的来源。
可将边界视为信息存储装置。根据全息原理,最大存储容量(或总比特数)与面积 A A A成正比。事实上,在涌现空间的理论中,面积可这样定义:每个基本比特占据一个单位格胞。
设已使用的比特数为 N N N,自然假设 N N N与面积成正比,因此可写为:
N = A c 3 G ℏ (3.10) N=\frac{A c^{3}}{G \hbar} \tag{3.10} N=GℏAc3(3.10)
其中我们引入了一个新常数 G G G------最终,该常数将被识别为牛顿引力常数。但由于我们尚未假设引力的存在,可将该方程简单视为 G G G的定义。因此,此处的唯一假设是"比特数与面积成正比",仅此而已。
假设系统中存在总能量 E E E,我们做一个简单假设:能量均匀分布在 N N N个比特上。根据均分定理,温度由下式确定 [ 4 ] ^{[4]} [4]:
E = 1 2 N k B T (3.11) E=\frac{1}{2} N k_{B} T \tag{3.11} E=21NkBT(3.11)
其中 E E E为每个比特的平均能量。接下来,我们仅需一个更多的方程:
E = M c 2 (3.12) E=M c^{2} \tag{3.12} E=Mc2(3.12)
其中 M M M表示屏幕所包围的空间部分中涌现的质量(如图3所示)。尽管该质量在已涌现的空间中并非直接可见,但其存在可通过能量间接感知。
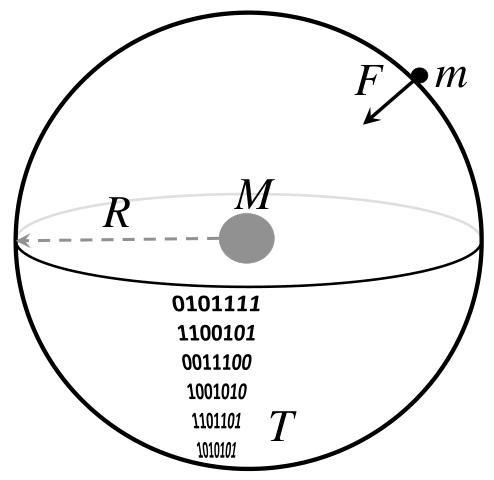
图3:球形全息屏幕附近有一个质量为 m m m的粒子。能量均匀分布在被占据的比特上,等效于屏幕所包围的空间部分中涌现的质量 M M M。
后续推导非常直接:消去 E E E,代入比特数的表达式以确定 T T T;然后利用熵变的假设(3.6)确定力;最后代入球面面积 A = 4 π R 2 A=4 \\pi R\^{2} A=4πR2,即可得到熟知的牛顿万有引力定律:
F = G M m R 2 (3.13) F=G \\frac{M m}{R\^{2}} \\tag{3.13} F=GR2Mm(3.13)
我们几乎从基本原理出发,恢复了牛顿万有引力定律!
这些方程的导出并非偶然:部分源于量纲分析,部分因为牛顿定律已成为推导黑洞热力学和全息原理的基础------在某种意义上,我们逆转了这些论证的逻辑。但本文的逻辑明显不同,它为引力的起源提供了新的视角:引力是一种熵力!这是一个新的、前所未有的核心结论------如果正确,它将具有深远的意义。
#### 3.3 推导的自然性与稳健性
我们的出发点是"空间具有一个涌现的全息方向",附加要素包括:(i)在涌现方向上存在熵变;(ii)自由度数量与屏幕面积成正比;(iii)能量均匀分布在这些自由度上。在此之后,产生的力必然呈现牛顿定律的形式。事实上,这一推理可推广到任意维度 \[ 4 \] \^{\[4\]} \[4\],结论保持不变。但这些启发性论证的稳健性和自然性如何?
或许最不明显的假设是均分定理------该定理通常仅适用于自由系统,但它是否至关重要?能量通常会根据某种非平凡的分布函数在微观自由度上传播,但当丢失的比特在所有比特中随机选择时,与 Δ S \\Delta S ΔS相关的能量变化仍应与单位面积能量 E / A E/A E/A成正比------因此,即使均分定理不严格成立,这一事实也可能成立。
为何在非相对论背景下需要光速 c c c?这是因为需要将质量 M M M转换为能量------而能量是熵力所需的热浴的来源。在非相对论情形下,热浴是无限的,但原则上,当粒子在外力作用下改变位置时,必须考虑热浴能量的得失------这将导致相对论红移(后续将详细讨论)。
由于假设(3.5)是所有后续推导的基础,我们进一步讨论其意义:为何当位移为一个康普顿波长时,熵变恰好如此?事实上,人们可能会疑惑:既然我们的目标只是推导经典牛顿定律,为何需要引入普朗克常数 ℏ \\hbar ℏ?确实, ℏ \\hbar ℏ最终会从最重要的公式中消去。因此,原则上可将 ℏ \\hbar ℏ乘以任意常数,仍能得到相同的结果。因此, ℏ \\hbar ℏ仅作为量纲所需的辅助变量,可任意选择,以确保式(3.5)严格成立。该方程的核心内容是:垂直于屏幕的熵变与质量 m m m和位移 Δ x \\Delta x Δx成正比------仅此而已。
如果我们远离屏幕,熵变的规律通常将不再相同。假设粒子保持在半径 R R R处,而屏幕被移动到 R 0 \< R R_{0}\ 接下来的问题是:如何获得作用在屏幕和质量分布外任意位置的物质粒子上的力?为此,需要将第一个假设(3.6)推广到这种情形。粒子的任意无穷小位移 δ r ⃗ i \delta \vec{r}{i} δr i导致的熵变是什么?这里只有一个自然的选择:我们希望找到屏幕 S S S上局域的熵密度变化 δ s \delta s δs。由式(3.16)可知,牛顿势 Φ \Phi Φ追踪着单位比特的信息变化------因此,熵密度变化的正确识别为: 其中 δ Φ \delta \Phi δΦ是粒子位置位移 δ r ⃗ i \delta \vec{r}{i} δr i引起的牛顿势响应。具体而言, δ Φ \delta \Phi δΦ通过求解泊松方程的变分得到: 可验证:当其中一个粒子接近屏幕时,这一识别确实能重现熵变(3.6)。 现在,我们确定测试粒子受到的熵力。所有力对测试粒子做的总功由热力学第一定律确定,但需要用局域温度和熵变表示: 为证明这确实能给出最一般情形下的引力,只需利用静电类比:可将整个质量 M M M重新分布为屏幕 S S S上的质量面密度,而不改变粒子受到的力。牛顿势的变分可通过拉普拉斯算子的格林函数获得。证明的其余部分是静电学的直接应用,只是将其应用于引力。需要证明的基本恒等式是: 该式适用于质量分布外的任意屏幕位置。利用斯托克斯定理和拉普拉斯方程,可轻松验证该式。当屏幕选择为等势面时,第二项消失:只需将 Φ \Phi Φ替换为 Φ 0 \Phi_{0} Φ0并从积分中提出------由于 δ Φ \delta \Phi δΦ仅由屏幕外的粒子源产生,剩余积分恰好为零。 我们得到的力与屏幕位置的选择无关:可选择任意等势面,得到的 F ⃗ i \vec{F}_{i} F i值均相同(即牛顿定律描述的力)。这一结果的有效性不仅取决于量纲分析,还与"特定位置对应于微观数据粗粒化尺度的任意选择"这一观点一致------宏观物理(特别是力)应与该选择无关。 由于我们的论证中使用了光速 c c c,将讨论推广到相对论情形是合乎逻辑的下一步。因此,我们假设微观理论满足洛伦兹对称性,甚至具有庞加莱群作为整体对称性------这意味着我们必须将时间和空间结合成一个几何结构。时空涌现的图景自然会导致广义协变性和弯曲几何------因为原则上不存在优选的坐标选择,也没有理由认为曲率不存在。具体而言,我们希望看到:爱因斯坦广义相对论如何从与前几节类似的推理中涌现------事实证明,这是可能的。但首先,我们研究惯性和等效原理的起源。 考虑具有全局类时基灵矢量 ξ a \xi^{a} ξa的静态背景。要理解惯性和等效原理的涌现,需将该基灵矢量场的选择与温度和熵梯度相关联。特别地,我们希望表明:粒子的通常测地线运动可被理解为熵力的结果。 在广义相对论中 [ 5 ] ^{[5]} [5],牛顿势的自然推广为 [ 11 ] ^{[11]} [11]: 其指数 e ϕ e^{\phi} eϕ表示红移因子,将局域时间坐标与无穷远处 ϕ = 0 \phi=0 ϕ=0的参考点的时间坐标关联起来。 与非相对论情形类似,我们希望利用 ϕ \phi ϕ定义空间的叶状化,并将全息屏幕放置在恒定红移的曲面上------这是一个自然的选择,因为在这种情况下,整个屏幕使用相同的时间坐标,因此屏幕上微观数据的处理可通过无时间延迟的信号进行。 我们希望表明:屏幕垂直方向的红移,可微观地理解为源于熵梯度 [ 6 ] ^{[6]} [6]。为明确这一点,考虑作用在质量为 m m m的粒子上的力。在广义相对论背景下,力的定义不太明确(因为它可通过广义坐标变换消去),但通过使用类时基灵矢量,可赋予力一个不变的意义 [ 11 ] ^{[11]} [11]。 粒子的四速度 u a u^{a} ua及其加速度 a b ≡ u a ∇ a u b a^{b} \equiv u^{a} \nabla_{a} u^{b} ab≡ua∇aub,可通过基灵矢量 ξ b \xi^{b} ξb表示为: 利用基灵方程 ∇ a ξ b + ∇ b ξ a = 0 \nabla_{a} \xi_{b}+\nabla_{b} \xi_{a}=0 ∇aξb+∇bξa=0和 ϕ \phi ϕ的定义,可进一步重写最后一个方程------发现加速度可再次简单表示为梯度: 注意,与非相对论情形类似,加速度垂直于屏幕 S S S。因此,可通过将其与屏幕 S S S的单位外法向矢量 N b N^{b} Nb(同时垂直于 ξ b \xi^{b} ξb)缩并,将其转换为标量。 屏幕上的局域温度 T T T,类比非相对论情形定义为: 此处引入红移因子 e ϕ e^{\phi} eϕ,因为温度 T T T是相对于无穷远处的参考点测量的。 为找到位于屏幕附近的粒子受到的力,我们再次使用第二节中的假设:当粒子垂直于屏幕位移一个康普顿波长时,屏幕上的熵变为 2 π 2 \pi 2π。因此: 其中负号源于"从外部穿越到内部时熵增加"这一事实。第三节3.3节中关于该假设有效性的评论同样适用于此处。熵力由式(5.28)可得: 这确实是将粒子保持在屏幕附近固定位置所需的正确引力(从无穷远处的参考点测量),是牛顿惯性定律 F = m a F=ma F=ma的相对论类比。额外的因子 e ϕ e^{\phi} eϕ源于红移------注意, ℏ \hbar ℏ再次消去。 将力方程(5.30)重写为微正则形式是有益的。设 S ( E , x a ) S(E, x^{a}) S(E,xa)为包含质量为 m m m的粒子(位于位置 x a x^{a} xa)的系统的总熵( E E E也包括粒子的能量)。熵通常还依赖于许多其他参数,但在本讨论中我们将其省略。 如第二节所述,熵力可在微正则系综中确定:手动添加外力项,并要求熵取极值。对于这种情况,该条件为: 容易验证,这将导出与式(5.30)相同的方程------该式确定了平衡点,此时由 ϕ ( x ) \phi(x) ϕ(x)表征的外力与熵力统计平衡。我们再次强调:此处不存在微观力的作用!与第二节中讨论的聚合物的式(2.4)的类比现在应该很明显了。 式(5.31)告诉我们:如果移动粒子并同时按红移因子减少其能量,熵将保持不变。这仅当粒子非常轻、不干扰其他能量分布时成立------它仅作为涌现几何的探针。这也意味着红移函数 ϕ ( x ) \phi(x) ϕ(x)完全由系统中的其他物质决定。 我们通过识别时空温度和熵变,得到了式(5.31)------但实际上,我们应该反向推导:从微观出发,用微观量定义空间相关的概念。我们选择不采用这种表述方式,因为它可能显得有些刻意。 但重要的是要认识到:红移应被视为熵梯度的结果,而非相反。等效原理告诉我们:在涌现时空中,红移既可解释为引力场的效应,也可解释为观测者处于加速参考系的效应------这两种观点在相对论背景下是等效的,但均非微观描述。加速度和引力都是涌现现象。 现在,我们希望将引力定律的推导推广到相对论情形,并获得爱因斯坦方程------这确实可以通过自然且高度类似的方式完成。因此,我们再次考虑闭合的恒定红移 ϕ \phi ϕ曲面上的全息屏幕,假设它包围着某个静态质量构型,总质量为 M M M。屏幕上的比特密度仍由下式给出: (与式(4.18)一致)。遵循与前文相同的逻辑,假设与质量 M M M相关的能量分布在所有比特上------再次通过均分定理,每个比特携带的质量单位为 1 2 T \frac{1}{2} T 21T。因此: 代入 T T T和 d N d N dN的表达式,可得: 如预期的那样, ℏ \hbar ℏ再次消去。式(5.34)确实是高斯定律到广义相对论的自然推广------右侧恰好是任意静态弯曲时空中任意体积内包含的质量的科马尔(Komar)定义。它可通过假设爱因斯坦方程推导得出,但在我们的推理中,我们从相反的方向出发:对屏幕上的温度和比特数进行识别,但尚不知道它是否满足任何场方程。此时的关键问题是:式(5.34)是否足以推导完整的爱因斯坦方程? 雅各布森(Jacobson)已针对零屏幕(null screens)解决了类似的问题 [ 7 ] ^{[7]} [7]。将他的推理适用于这种情况,并结合沃尔德(Wald)对科马尔质量的阐述,可直接构建一个自然导出爱因斯坦方程的论证------以下是论证的概要: 首先,利用科马尔质量可通过基灵矢量 ξ a \xi^{a} ξa表示这一事实: 左侧可表示为应力-能量张量 T a b T_{a b} Tab的某些分量在包围体积上的积分;右侧首先利用斯托克斯定理,随后利用由 ξ a \xi^{a} ξa的基灵方程导出的关系: 这导致积分关系 [ 11 ] ^{[11]} [11]: 其中 ∑ \sum ∑是由全息屏幕 S S S界定的三维体积, n a n^{a} na是其法向。左侧应力-能量张量的特定组合,大概可通过比较两侧的性质(例如积分中张量的守恒律)来确定。 该方程在具有类时基灵矢量 ξ a \xi^{a} ξa的一般静态背景下推导得出。要求它对任意屏幕成立,意味着两侧的被积函数也必须相等------这仅给出了爱因斯坦方程的某个分量。事实上,我们可以以多种方式选择曲面 ∑ \sum ∑(只要其边界为 S S S),这意味着我们可以改变法向 n a n^{a} na------但仍存在与基灵矢量 ξ a \xi^{a} ξa的缩并。 为得到完整的爱因斯坦方程,我们现在使用与雅各布森 [ 7 ] ^{[7]} [7]类似的推理,但应用于类时屏幕:考虑时空的一个非常小的区域,并关注非常短的时间尺度。由于局域上所有几何都近似为闵可夫斯基空间,可选择近似的类时基灵矢量。现在考虑屏幕的一个小局域部分,并要求:当物质穿过它时,科马尔积分的值恰好跳跃相应的质量 m m m。通过遵循上述步骤,可对所有这些基灵矢量和任意屏幕得到式(5.37)------这足以获得完整的爱因斯坦方程。 本节最后,我们解释熵力如何作用在远离屏幕和质量分布的任意位置 x i x_{i} xi的粒子集合上。科马尔质量的定义再次对此有用------科马尔质量依赖于基灵矢量 ξ a \xi_{a} ξa的选择,特别是其范数(红移因子 e ϕ e^{\phi} eϕ)。如果将粒子进行虚位移 δ x i \delta x_{i} δxi,这将影响屏幕内物质构型的科马尔质量的定义------事实上,屏幕上的温度将直接受到红移因子变化的影响。 虚位移可准静态地进行------这意味着基灵矢量本身仍然存在,但其范数(或红移因子)可能发生变化。事实上,空间度规也可能受到该位移的影响。我们不会尝试解决这些依赖关系(由于爱因斯坦方程的非线性,这是不可能的),但我们可以简单地利用"科马尔质量将是粒子位置 x i x_{i} xi的函数"这一事实。 接下来,我们假设:除了科马尔质量对 x i x_{i} xi的依赖外,整个系统的熵也明确依赖于 x i x_{i} xi------这源于信息量的变化。这正是我们希望确定的熵力的来源。我们现在基于最大熵原理,给出熵依赖性的自然处方------它确实能给出正确的力:假设熵可表示为科马尔质量 M M M和 x i x_{i} xi的函数,但由于科马尔质量应被视为位置 x i x_{i} xi的函数 M ( x i ) M(x_{i}) M(xi),熵中将存在明确的和隐含的 x i x_{i} xi依赖。最大熵原理意味着这两种依赖应相互抵消,因此我们施加: 展开这一条件,并分离每个变分 δ x i \delta x^{i} δxi所隐含的方程,可得: 关键点在于:第一项表示屏幕内质量分布对第 i i i个粒子施加的力------由于能量守恒,它确实等于科马尔质量的导数的负值。但同样,这并非力的微观原因。与聚合物类似,科马尔质量代表热浴的能量------它对其他粒子位置的依赖,源于红移(其微观起源在于热浴能量因熵效应而损耗)。 由于科马尔积分在全息屏幕上定义,显然与非相对论情形类似,力也可表示为该屏幕上的积分------我们没有尝试使这一表示更具体。最后,我们注意到:这一论证非常一般,并未真正使用科马尔积分或爱因斯坦方程的精确形式。因此,利用沃尔德的诺特定理电荷形式主义 [ 12 ] ^{[12]} [12],将这一推理推广到高阶导数引力理论应该是直接的------该形式主义非常适合这一目的。 本文提出的观点和结果引发了诸多问题------本节将讨论并尝试回答其中一些,首先给出主要结论。 引力已给出诸多"它是涌现现象"的线索,但迄今为止,它仍被视为基本力。它与其他已知涌现现象(如热力学和流体力学)的相似性,大多仅被视为启发性类比------现在,我们不仅要注意到这种类比、谈论这种相似性,更要最终摒弃"引力是基本力"的观点。 当然,爱因斯坦对引力的几何描述既优美又在某种意义上令人信服。几何诉诸我们思维的视觉部分,在总结物理问题的诸多方面时具有惊人的威力------这可能解释了为何我们作为一个科研群体,如此不愿放弃"引力的几何表述是基本的"这一观点。但我们必须这样做:如果引力是涌现的,时空几何也是涌现的。爱因斯坦将这两个概念紧密联系在一起------如果我们希望在更基本的层面上理解其中之一,就必须同时放弃两者。 本文的结果表明:一旦空间和时间本身涌现,引力就会作为熵力出现。如果引力和时空确实可被解释为涌现现象,这将对引力起核心作用的诸多领域产生重要影响------探索其对宇宙学的影响将特别有趣。例如,红移源于熵梯度的方式,可能带来许多新的见解。 本文对爱因斯坦方程的推导与先前的工作(特别是文献 [ 7 ] ^{[7]} [7])类似。其他作者也提出过"引力具有熵性或热力学起源"的观点(例如文献 [ 14 ] ^{[14]} [14]),但我们添加了一个重要的新要素:不仅关注支配引力场的方程,还揭示了"在空间涌现的背景下,力和惯性的起源"。我们确定了引力的一个原因、一种机制------它由熵差驱动(无论熵如何定义),是微观层面统计平均的随机动力学的结果。现在,引力为何必须同时追踪能量和熵差的原因已很明确:因为这正是导致运动的根源! 必须承认,本文的论证具有一定的启发性------考虑到我们正在进入一个"空间原本不存在"的未知领域,这是不可避免的。这些问题的深刻性,证明了这种启发性推理的合理性。我们做出的假设是自然的:它们与现有观点一致,并得到多项证据支持。以下,我们从弦理论、AdS/CFT对偶和黑洞物理中收集更多支持证据。 如果引力只是一种熵力,这对弦理论意味着什么?引力被视为弦理论的一个组成部分,不能轻易移除------但我们知道,含引力的闭弦理论与解耦的不含引力的开弦理论之间存在对偶性,AdS/CFT对偶是一个尤为重要的例子。 开弦/闭弦对偶和AdS/CFT对偶,是弦理论中根深蒂固的紫外/红外关联的体现------这种关联意味着短程和长程物理不能被视为完全解耦。引力是一种长程现象,但显然与短程物理相关(因为牛顿常数是微观自由度数的度量)。弦理论否定了威尔逊有效场论的"普遍认知"------即积分掉短程自由度仅会在有效作用量中产生局域项,其中大多数在低能下无关紧要。如果这完全正确,宏观物理将对短程物理不敏感。 威尔逊论证失败的原因,是它对高能态数量的渐近增长做了过于保守的假设。在弦理论中,高能开弦态的数量如此之多,以至于积分掉它们确实会导致长程效应------它们的单圈振幅,等效于闭弦态交换的树图贡献(其中包括引力的贡献)。然而,这种相互作用也可等效地表示为开弦所有量子贡献的总和------在这个意义上,弦理论也支持引力的涌现性质。 AdS/CFT对偶在"引力并非基本存在"的物理领域的应用日益广泛:引力技术被用作工具,以计算微观描述失效区域的物理量------最新的进展是将其应用于凝聚态理论。没有人怀疑,在这些情况下,引力仅作为有效描述涌现------它并非存在于微观理论的同一空间中,而是存在于具有额外维度的全息图景中。目前,对于这种引力的来源,尚无明确的解释------本文描述的熵机制应适用于这些物理系统,并解释引力的涌现。 本文讨论的全息图景,无疑受到了AdS/CFT对偶和开弦/闭弦对偶中全息原理工作方式的启发。用弦论的语言来说,全息屏幕可被识别为D-膜,屏幕上的微观自由度表示为在紫外截断下定义的开弦。已涌现的空间部分由闭弦占据,这些闭弦也在紫外截断下定义(如图6所示)。开弦和闭弦的截断通过紫外/红外关联相关联:将开弦截断推向紫外,会迫使闭弦截断推向红外,反之亦然。截断的值由屏幕的位置决定。积分掉开弦会产生闭弦,并导致空间和引力的涌现。然而,从我们的角度来看,引力或闭弦的存在并非在微观上假设的------它们作为有效描述涌现。 图6 a)中的微观理论可由 b)所示的、由开弦和闭弦构成的弦理论有效描述,两类弦均存在紫外截断。 通过这种方式,开弦/闭弦对偶支持"引力是熵力"的解释。然而,许多人仍将这些对偶性的闭弦侧视为定义明确的基本理论------但在我们看来,引力和闭弦是涌现的,仅作为宏观概念存在。巧合的是,在我们理解"它们可从不含引力的微观理论中获得"之前,就已经知晓了引力。我们不禁联想到:如果在了解原子之前半个世纪,我们就已经利用连续介质中的应力张量发展出了弹性理论,我们可能也会同样抗拒接受"弹性是涌现的"这一显而易见的事实。引力和闭弦与此类似,我们只是尚未习惯"它们是涌现的"这一观点。 关于"引力是熵力"这一结论,我们或许把最直观的论证留到了最后。当贝肯斯坦、霍金等人发现黑洞热力学定律时,引力作为基本力的认知首次出现裂痕。事实上,第三节中提及的、促使贝肯斯坦推导出熵定律的思想实验,与聚合物的熵力案例有着惊人的相似性:黑洞扮演热浴的角色,而靠近黑洞的粒子,可类比为被拉开后逐渐回归平衡态的聚合物端点。 诚然,引力系统中并不存在聚合物,粒子与黑洞之间也没有直接的相互接触------但我们在此忽略了一个关键前提:时空的其中一个维度是涌现的。从全息描述的视角来看,这一过程中的粒子实则相当于浸入了代表黑洞的热浴之中,这一点在AdS/CFT对偶中体现得尤为鲜明:黑洞与边界上的热态互为对偶,而粒子则对应一个逐渐热化的非定域算符。当粒子抵达黑洞视界时,便会融入这一热态,与聚合物回归卷曲的平衡构型如出一辙。这一现象的本质显然是熵驱动的,是系统在统计规律下趋向最大熵状态的必然结果。 深入分析贝肯斯坦的推理过程可以证明,在黑洞视界附近,引力完全以熵力的形式存在,且本文第三节推导的所有方程在该区域均严格成立。贝肯斯坦的核心观点是,需在距离黑洞视界约一个康普顿波长的位置,将粒子与黑洞视为一个整体系统。我们不妨将这一位置视作一个全息屏幕的所在处,而该屏幕的精确位置并不重要------因为不存在任何自然的优选距离,因此推导得到的方程也不应随该距离的微小变化而改变。 将粒子从这一位置再向外拉远少许,其能量的变化量恰好等于引力对其做的功。若此时将粒子投入黑洞,黑洞的总质量 M M M也会增加相同的量。结合黑洞热力学定律的自洽性要求,贝肯斯坦-霍金熵的增量与霍金温度 T H T_H TH的乘积,必然等于引力所做的功,即: 式中熵的偏导数,表示黑洞熵 S B H S_{BH} SBH随粒子到视界距离 x x x的变化率。这一关系虽已为人熟知,往往仅被视作黑洞热力学的自洽性验证,但我们可以基于此进一步深挖其物理本质。 假设我们将全息屏幕移至距离视界更远的位置,上述论证依然成立;但我们也可以忽略屏幕的移动,将粒子从新屏幕的位置重新放至原屏幕(更靠近视界)的位置。这一过程发生在新屏幕所围区域的内部空间,因此其全息描述完全可以体现在新屏幕之上。在这一全息描述中,垂直于屏幕方向的"力"并无任何微观物理意义,对应的"加速度"亦是如此------垂直于屏幕的坐标 x x x,本质上只是与粒子的全息成像相关的标度参量,其作为时空坐标的物理意义,实则是涌现而来的,而这正是时空涌现的核心内涵。 粒子的质量,由其全息成像对应的能量定义,这一能量状态近似为热平衡态,但并非严格的热平衡------因为粒子仍处于视界之外的微小距离处,就像被拉开的聚合物偏离了平衡构型一般。我们不禁要问:在涌现的时空中,将粒子从新屏幕位置缓慢移至原屏幕位置的过程中,引力做功对应的全息能量变化,其微观起源究竟是什么?答案必然是熵效应:这一过程中的力,本质上源于系统的热化过程。我们由此得出一个必然结论:这一现象唯一的微观解释,就是存在一种涌现的熵力。事实上,标度参量与能量的全息对应关系,和涌现时空坐标 x x x、粒子质量 m m m的物理对应关系,必然满足熵力公式 F = T ∇ S F=T \nabla S F=T∇S向引力的直接转化,而本文第三节给出的温度与熵变的相关方程,也恰好能完美实现这一转化。 黑洞视界的特殊性,仅针对于视界外的观测者而言。无论黑洞的质量多大,其视界处的引力场多微弱,上述论证均成立。因此,这一思想实验揭示的并不仅仅是黑洞的物理性质,更关乎时空的本质与引力的起源,或者更确切地说,揭示了惯性的熵起源 。将这一思想实验应用于林德勒视界,我们能得到完全相同的结论:此时的全息对应关系,会将熵力公式 F = T ∇ S F=T \nabla S F=T∇S直接转化为惯性力的公式 F = m a F=ma F=ma,相关推导仍与本文第三节的结论一致。 这引出了一个尚未被完全理解的微妙问题------即普朗克常数 ℏ \hbar ℏ的作用。前文的论证表明,在视界附近,当 ℏ \hbar ℏ被识别为实际的普朗克常数时,方程是成立的。然而,我们没有直接的证据或证明表明,当远离视界(尤其是当完全不存在视界时),情况也是如此。事实上,有理由认为方程在这些区域的作用方式略有不同:首先,系统并非完全处于热平衡状态------视界具有明确的温度,显然处于热平衡,但如果假设等势面 Φ = Φ 0 \Phi=\Phi_0 Φ=Φ0上的屏幕处于平衡状态,那么获得昂鲁温度(3.8)所需的熵由贝肯斯坦-霍金公式给出(包含因子 1 / 4 1/4 1/4): 这一熵值似乎非常高,违反了贝肯斯坦界 [ 15 ] ^{[15]} [15]------该界指出,包含在半径为 R R R、总能量为 E E E的区域内的系统,其熵不能超过 E R ER ER。这种差异的原因可能是:贝肯斯坦的论证不适用于屏幕上的全息自由度,或者因为系统远未达到平衡。 但也可能存在其他调和这些陈述的方式,例如利用重新标度 ℏ \hbar ℏ的自由度------这不会影响力的最终结果,也不会改变其熵性本质。事实上,甚至可以将 ℏ \hbar ℏ乘以屏幕上牛顿势的函数 f ( Φ 0 ) f(\Phi_0) f(Φ0):这种标度变换会以相反的方向影响熵和温度的值( T T T乘以一个因子,而 S S S除以同一个因子)。由于我们无法先验地排除这种可能性,这一问题仍有待进一步研究。此外,还可能存在其他修正方式,例如采用多个不同温度屏幕的加权平均描述------即便如此,我们结论的核心(引力和惯性是熵力)仍不会改变。 这种引力观是否能做出预测?统计平均应给出通常的定律,因此必须研究引力的涨落------涨落的大小取决于有效温度(可能并非普适,而是依赖于 ℏ \hbar ℏ的有效值)。一个有趣的想法是:在小质量物体之间的弱引力场中,涨落可能会更加显著。但显然,我们需要对该理论有更深入的理解,才能将其转化为可验证的预测。 众所周知,牛顿曾受到同时代人的批评(尤其是胡克),认为他的万有引力定律是超距作用,没有像弹性力那样直接的力学成因。具有讽刺意味的是,这正是胡克的弹性力如今不被视为基本力,而牛顿的引力却维持这一地位超过三个世纪的原因。牛顿当时并不知道(胡克当然也不知道)宇宙是全息的------全息原理本身也是一种假设,可能看起来和超距作用一样荒谬。 本文的核心观点之一是:全息假设为引力的涌现提供了自然的机制。它允许与一个物体相关的自由度与另一个物体的自由度发生直接"接触"相互作用------因为一个体积内的所有物体都可以映射到同一个全息屏幕上。一旦做到这一点,牛顿引力和胡克弹性的机制就惊人地相似。我们猜想,这两位竞争对手都不会对这一结论感到满意。 本研究部分得到了荷兰基础研究基金会(Stichting FOM)的支持。我要感谢J.德布尔(J. de Boer)、B.乔杜里(B. Chowdhuri)、R.迪杰格拉夫(R. Dijkgraaf)、P.麦克法登(P. McFadden)、G.特霍夫特(G. 't Hooft)、B.尼恩休伊斯(B. Nienhuis)、J.-P.范德沙尔(J.-P. van der Schaar),尤其要感谢M.重森(M. Shigemori)、K.帕帕多迪马斯(K. Papadodimas)和H.韦尔林德(H. Verlinde)的讨论和评论。 1\] J. D. 贝肯斯坦(J. D. Bekenstein),《黑洞与熵》(Black holes and entropy),《物理评论D》(Phys. Rev. D),7卷,2333页(1973)。
\[2\] J. M. 巴丁(J. M. Bardeen)、B. 卡特(B. Carter)和S. W. 霍金(S. W. Hawking),《黑洞力学四定律》(The Four laws of black hole mechanics),《数学物理通讯》(Commun. Math. Phys.),31卷,161页(1973)。
\[3\] S. W. 霍金(S. W. Hawking),《黑洞的粒子产生》(Particle Creation By Black Holes),《数学物理通讯》(Commun. Math. Phys.),43卷,199-220页(1975)。
\[4\] P. C. W. 戴维斯(P. C. W. Davies),《史瓦西和林德勒度规中的标量粒子产生》(Scalar particle production in Schwarzschild and Rindler metrics),《物理学报A》(J. Phys. A),8卷,609页(1975)。
\[5\] W. G. 昂鲁(W. G. Unruh),《黑洞蒸发笔记》(Notes on black hole evaporation),《物理评论D》(Phys. Rev. D),14卷,870页(1976)。
\[6\] T. 达穆尔(T. Damour),《黑洞物理中的表面效应》(Surface effects in black hole physics),收录于《第二届马塞尔·格罗斯曼广义相对论会议论文集》(Proceedings of the Second Marcel Grossmann Meeting on General Relativity),R. 鲁菲尼(R. Ruffini)主编,北荷兰出版社(North Holland),587页(1982)。
\[7\] T. 雅各布森(T. Jacobson),《时空热力学:爱因斯坦状态方程》(Thermodynamics of space-time: The Einstein equation of state),《物理评论快报》(Phys. Rev. Lett.),75卷,1260页(1995)。
\[8\] G. 特霍夫特(G. 't Hooft),《量子引力中的降维》(Dimensional reduction in quantum gravity),arXiv:gr-qc/9310026。
\[9\] L. 萨斯坎德(L. Susskind),《世界作为全息图》(The World As A Hologram),《数学物理期刊》(J. Math. Phys.),36卷,6377页(1995)\[arXiv:hep-th/9409089\]。
\[10\] J. M. 马尔达西那(J. M. Maldacena),《超共形场论和超引力的大N极限》(The large N limit of superconformal field theories and supergravity),《高等理论物理杂志》(Adv. Theor. Math. Phys.),2卷,231页(1998)\[《国际理论物理杂志》(Int. J. Theor. Phys.),38卷,1113页(1999)\]。
\[11\] R. M. 沃尔德(R. M. Wald),《广义相对论》(General Relativity),芝加哥大学出版社(The University of Chicago Press),1984年。
\[12\] R. M. 沃尔德(R. M. Wald),《黑洞熵是诺特定理电荷》(Black hole entropy is the Noether charge),《物理评论D》(Phys. Rev. D),48卷,3427页(1993)\[arXiv:gr-qc/9307038\]。
\[13\] L. 萨斯坎德(L. Susskind),《弦理论的人择景观》(The anthropic landscape of string theory),arXiv:hep-th/0302219。
\[14\] T. 帕德马纳班(T. Padmanabhan),《引力的热力学方面:新见解》(Thermodynamical Aspects of Gravity: New insights),arXiv:0911.5004 \[gr-qc\],及其中参考文献。
\[15\] J. D. 贝肯斯坦(J. D. Bekenstein),《有界系统熵能比的普适上限》(A Universal Upper Bound On The Entropy To Energy Ratio For Bounded Systems),《物理评论D》(Phys. Rev. D),23卷,287页(1981)。
4.2 任意粒子位置的引力
δ s = k B δ Φ 2 c 2 d N (4.22) \delta s=k{B} \frac{\delta \Phi}{2 c^{2}} d N \tag{4.22} δs=kB2c2δΦdN(4.22)
∇ 2 δ Φ ( r ⃗ ) = 4 π G ∑ i m i δ r ⃗ i ⋅ ∇ i δ ( r ⃗ − r ⃗ i ) (4.23) \nabla^{2} \delta \Phi(\vec{r})=4 \pi G \sum{i} m_{i} \delta \vec{r}{i} \cdot \nabla{i} \delta\left(\vec{r}-\vec{r}_{i}\right) \tag{4.23} ∇2δΦ(r )=4πGi∑miδr i⋅∇iδ(r −r i)(4.23)
∑ i F ⃗ i ⋅ δ r ⃗ i = ∫ S T δ s (4.24) \sum_{i} \vec{F}{i} \cdot \delta \vec{r}{i}=\int_{\mathcal{S}} T \delta s \tag{4.24} i∑F i⋅δr i=∫STδs(4.24)
∑ i F ⃗ i ⋅ δ r ⃗ i = 1 4 π G ∫ S ( δ Φ ∇ Φ − Φ ∇ δ Φ ) d A (4.25) \sum_{i} \vec{F}{i} \cdot \delta \vec{r}{i}=\frac{1}{4 \pi G} \int_{\mathcal{S}}(\delta \Phi \nabla \Phi-\Phi \nabla \delta \Phi) d A \tag{4.25} i∑F i⋅δr i=4πG1∫S(δΦ∇Φ−Φ∇δΦ)dA(4.25)五、等效原理与爱因斯坦方程
5.1 惯性定律与等效原理
ϕ = 1 2 log ( − ξ a ξ a ) (5.26) \phi=\frac{1}{2} \log \left(-\xi^{a} \xi_{a}\right) \tag{5.26} ϕ=21log(−ξaξa)(5.26)
u b = e − ϕ ξ b , a b = e − 2 ϕ ξ a ∇ a ξ b u^{b}=e^{-\phi} \xi^{b}, \quad a^{b}=e^{-2 \phi} \xi^{a} \nabla_{a} \xi^{b} ub=e−ϕξb,ab=e−2ϕξa∇aξb
a b = − ∇ b ϕ (5.27) a^{b}=-\nabla^{b} \phi \tag{5.27} ab=−∇bϕ(5.27)
T = ℏ 2 π e ϕ N b ∇ b ϕ (5.28) T=\frac{\hbar}{2 \pi} e^{\phi} N^{b} \nabla_{b} \phi \tag{5.28} T=2πℏeϕNb∇bϕ(5.28)
∇ a S = − 2 π m ℏ N a (5.29) \nabla_{a} S=-2 \pi \frac{m}{\hbar} N_{a} \tag{5.29} ∇aS=−2πℏmNa(5.29)
F a = T ∇ a S = − m e ϕ ∇ a ϕ (5.30) F_{a}=T \nabla_{a} S=-m e^{\phi} \nabla_{a} \phi \tag{5.30} Fa=T∇aS=−meϕ∇aϕ(5.30)
d d x a S ( E + e ϕ ( x ) m , x a ) = 0 (5.31) \frac{d}{d x^{a}} S\left(E+e^{\phi(x)} m, x^{a}\right)=0 \tag{5.31} dxadS(E+eϕ(x)m,xa)=0(5.31)5.2 爱因斯坦方程的推导
d N = d A G ℏ (5.32) d N=\frac{d A}{G \hbar} \tag{5.32} dN=GℏdA(5.32)
M = 1 2 ∫ S T d N (5.33) M=\frac{1}{2} \int_{\mathcal{S}} T d N \tag{5.33} M=21∫STdN(5.33)
M = 1 4 π G ∫ S e ϕ ∇ ϕ ⋅ d A (5.34) M=\frac{1}{4 \pi G} \int_{\mathcal{S}} e^{\phi} \nabla \phi \cdot d A \tag{5.34} M=4πG1∫Seϕ∇ϕ⋅dA(5.34)
M = 1 8 π G ∫ S d x a ∧ d x b ϵ a b c d ∇ c ξ d (5.35) M=\frac{1}{8 \pi G} \int_{\mathcal{S}} d x^{a} \wedge d x^{b} \epsilon_{a b c d} \nabla^{c} \xi^{d} \tag{5.35} M=8πG1∫Sdxa∧dxbϵabcd∇cξd(5.35)
∇ a ∇ a ξ b = − R a b ξ a (5.36) \nabla^{a} \nabla_{a} \xi^{b}=-R_{a}^{b} \xi^{a} \tag{5.36} ∇a∇aξb=−Rabξa(5.36)
2 ∫ ∑ ( T a b − 1 2 T g a b ) n a ξ b d V = 1 4 π G ∫ ∑ R a b n a ξ b d V (5.37) 2 \int_{\sum}\left(T_{a b}-\frac{1}{2} T g_{a b}\right) n^{a} \xi^{b} d V=\frac{1}{4 \pi G} \int_{\sum} R_{a b} n^{a} \xi^{b} d V \tag{5.37} 2∫∑(Tab−21Tgab)naξbdV=4πG1∫∑RabnaξbdV(5.37)5.3 任意位置粒子集合受到的力
S ( M ( x i + δ x i ) , x i + δ x i ) = S ( M ( x i ) , x i ) (5.38) S\left(M\left(x_{i}+\delta x_{i}\right), x_{i}+\delta x_{i}\right)=S\left(M\left(x_{i}\right), x_{i}\right) \tag{5.38} S(M(xi+δxi),xi+δxi)=S(M(xi),xi)(5.38)
∇ i M + T ∇ i S = 0 (5.39) \nabla_{i} M+T \nabla_{i} S=0 \tag{5.39} ∇iM+T∇iS=0(5.39)六、结论与讨论
6.1 引力作为基本力的终结
6.2 对弦理论的影响及与AdS/CFT的关系
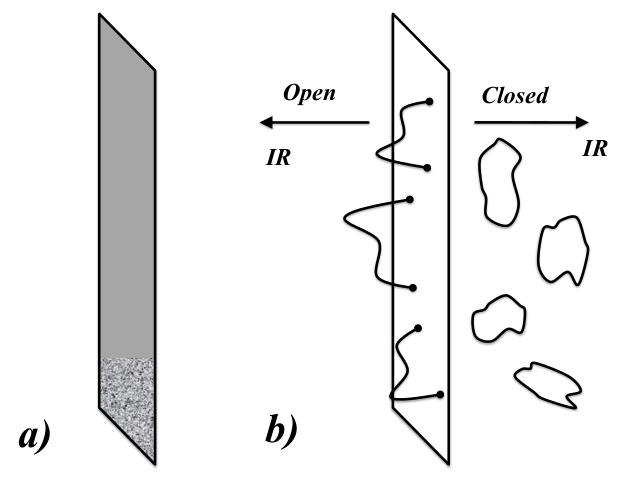
6.3 重新审视黑洞视界
F 引力 = T H ∂ S B H ∂ x (6.40) F_{\text{引力}}=T_{H} \frac{\partial S_{BH}}{\partial x} \tag{6.40} F引力=TH∂x∂SBH(6.40)6.4 最终讨论
S = c 3 4 G ℏ ∫ S d A (6.41) S=\frac{c^{3}}{4 G \hbar} \int_{\mathcal{S}} d A \tag{6.41} S=4Gℏc3∫SdA(6.41)致谢
参考文献