98. 验证二叉搜索树

中等

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含严格小于 当前节点的数。
节点的右子树只包含 严格大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

复制代码

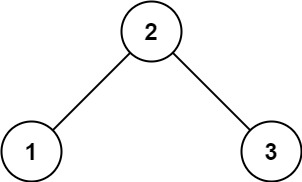
输入：root = [2,1,3]
输出：true

示例 2：

复制代码

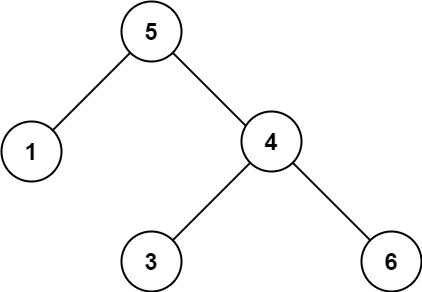
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1

📝 核心笔记：验证二叉搜索树 (Validate BST)

1. 核心思想 (一句话总结)

"给每个节点画一个圈：你必须活在祖先给你划定的界限(min, max)里。"

BST 的定义 ：不仅左儿子要小于爸爸，左子树的所有节点都要小于爸爸。
策略：

- 往左走：上界变紧（不能超过当前节点值），下界不变。
- 往右走：下界变紧（必须大于当前节点值），上界不变。

2. 算法流程 (区间收缩)

初始化 ：根节点的范围是无穷大 (Long.MIN, Long.MAX)。
当前检查：

- node.val 必须严格大于 left。
- node.val 必须严格小于 right。
- 如果不满足，直接 false。

递归传递：

- isValidBST(node.left, left, node.val)：左孩子的最大值被限制在 node.val。
- isValidBST(node.right, node.val, right)：右孩子的最小值被限制在 node.val。

🔍 代码回忆清单

复制代码

// 题目：LC 98. Validate Binary Search Tree
class Solution {
    public boolean isValidBST(TreeNode root) {
        // 1. 初始范围：使用 Long 防止 int 溢出
        // 如果树里有一个节点是 Integer.MAX_VALUE，用 int 作为边界就会判断错误
        return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }

    private boolean isValidBST(TreeNode node, long left, long right) {
        // 2. Base Case: 空节点被认为是合法的 BST
        if (node == null) {
            return true;
        }
        
        long x = node.val;
        
        // 3. 核心判断：当前值是否在 (min, max) 开区间内
        // 注意 BST 通常定义为严格小于/大于，所以不能有等号
        return left < x && x < right &&
               // 4. 递归检查左右子树，同时更新边界
               isValidBST(node.left, left, x) &&  // 往左走，天花板变成 x
               isValidBST(node.right, x, right);  // 往右走，地板变成 x
    }
}

⚡ 快速复习 CheckList (易错点)

为什么用 long**？**

- 面试必问 。如果根节点是 2147483647 (Integer.MAX_VALUE)。
- 如果用 int max = Integer.MAX_VALUE，那么右子树的判断逻辑 val < max 对于最大整数会失效（或者很难区分是边界还是节点值）。用 long 可以轻松包容所有 int。

局部 vs 全局？

- 初学者最容易犯的错是只写 if (root.left.val < root.val)。
- 反例：
  
  5
  /
  1 4 <-- 4 比 5 小，但它在右边！错误！
  /
  3 6
- 您的代码通过传递 left 和 right 参数，成功阻止了 4 出现在 5 的右边（因为右边节点的下界必须是 5）。

🖼️ 数字演练

树：

复制代码

Check 5 : Range (-inf, +inf). OK.

- Recurse Left: Range (-inf, 5).
- Recurse Right: Range (5, +inf).

Check 7 (Right) : Range (5, +inf). 5 < 7 < inf. OK.

- Recurse Left (Node 4): Range (5, 7).

Check 4:

- Is 5 < 4 < 7? NO!
- Return false.