dfs专题8——子集

🔥近津薪荼： 个人主页 🎬个人专栏： 《近津薪荼的算法日迹》 《Linux操作系统及网络基础知识分享》 《c++基础知识详解》 《c语言基础知识详解》 ✨不要物化，矮化，弱化，钝化自己，保持锋芒，不要停止学习 这个世界上只有两个人真正在注意着你 八岁的你，和八十岁的你， 他们此刻正在注视着你， 一个希望你 勇敢开始 ，一个希望你 不留遗憾

---

1.上期参考代码

class Solution {

vector<vector<int>>ret;
vector<int>path;
vector<bool>check=vector<bool>(6, false);
public:
    vector<vector<int>> permute(vector<int>& nums) {
        dfs(nums);
        return ret;
    }
    void dfs(vector<int>& nums)
    {
        if(path.size()==nums.size())
        {
            ret.push_back(path);
            return;
        }
        for(int i=0;i<nums.size();i++)
        {
            if(check[i]==false)
            {
                path.push_back(nums[i]);
                check[i]=true;
                dfs(nums);

                //回溯
                check[i]=false;
                path.pop_back();
            }
        }
    }
};

2.本期知识点导图

3.本期要讲解的题目是

子集

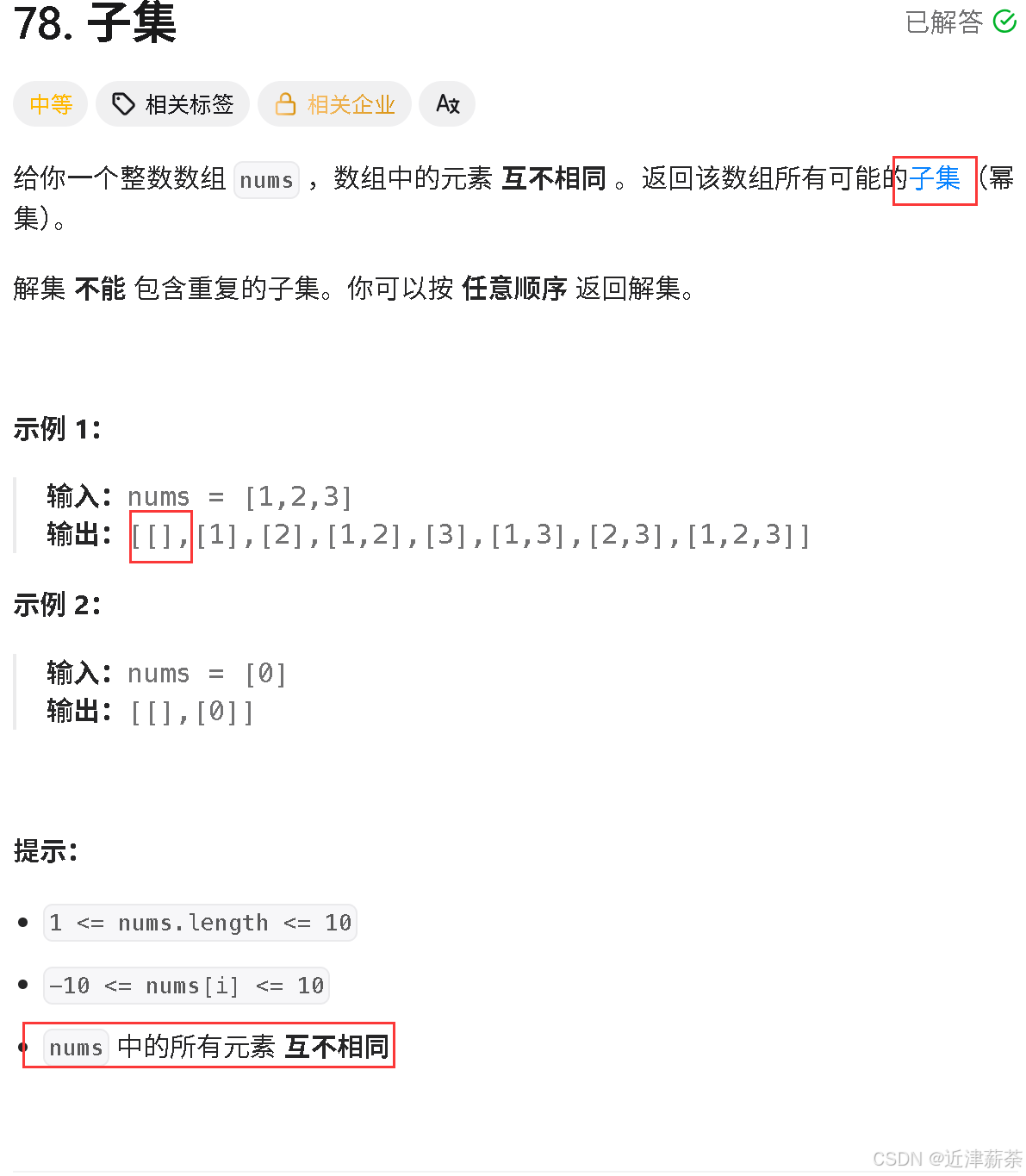
要点：

• nums元素各异
• 要返回空集

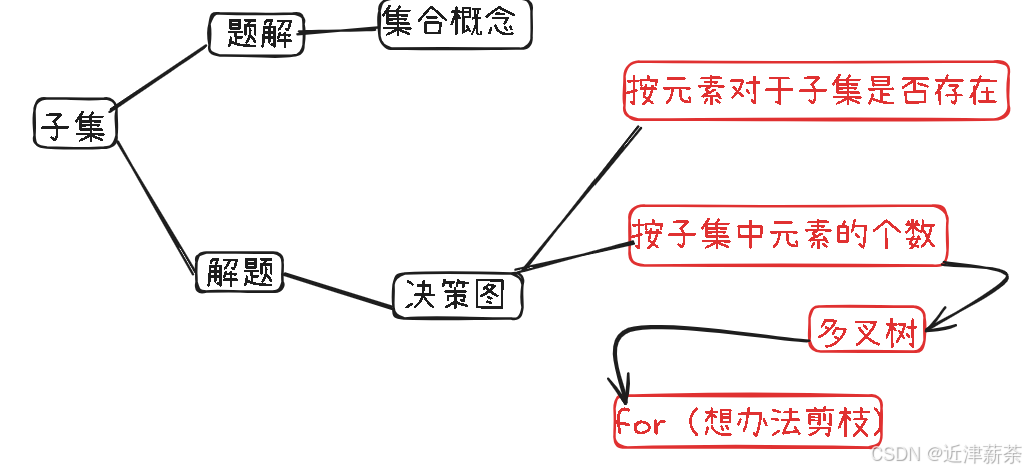
4.解题

本题我们可以画出两种决策树

4.1决策树1

高中，我们学集合的时候知道，一个集合的子集个数为2ⁿ个，这个2ⁿ怎么来的？

在一个元素对于集合来说，只有两种情况：存在或者不存在

对于每一个元素进行存在或者不存正在的划分，我们可以得出以下的决策图：

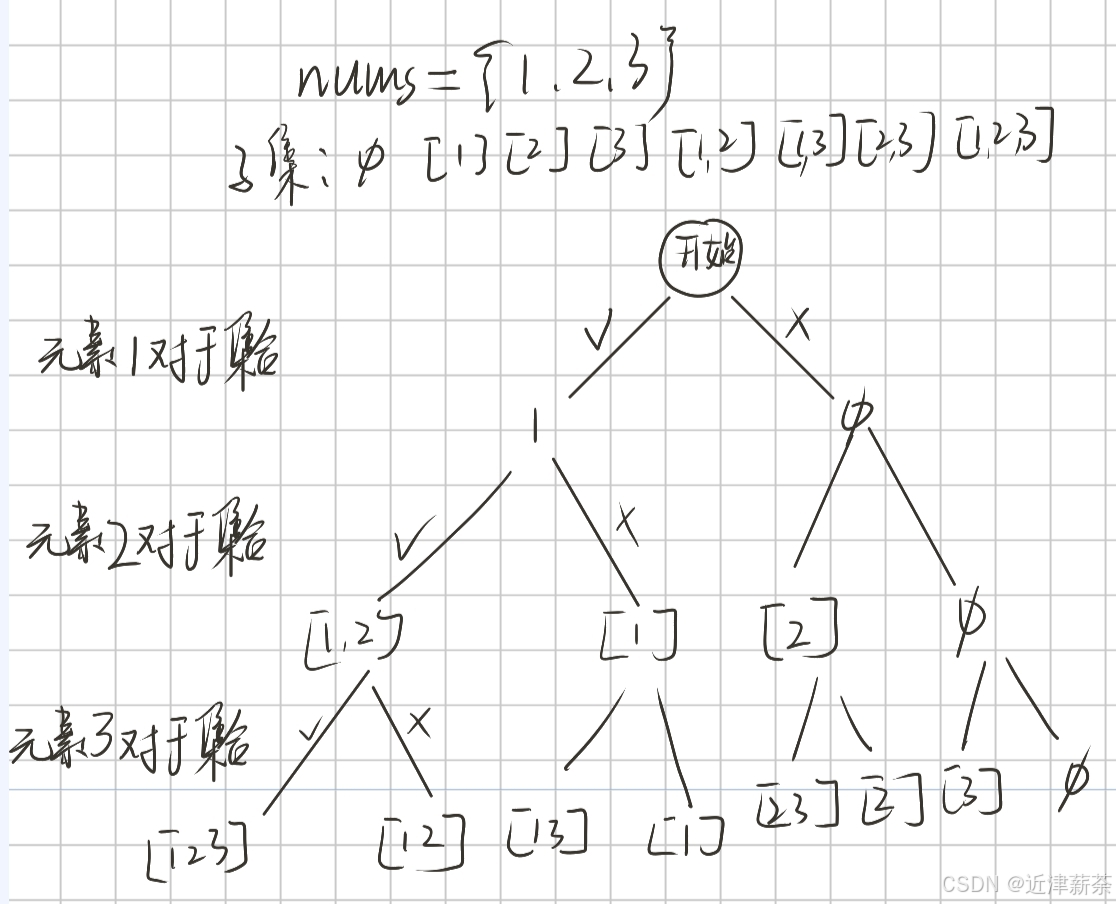
我们发现决策树的结果完全符合我们的期望，所以这就是一个好的决策树。

有了决策树，根据其写代码就方便多啦~

根据决策树，我们得出需要

两个全局变量：

• 上一级已经存放了的元素-->变量path（也可以设置成函数参数，避免返回现场操作）

• 存放path的二维数组用于返回所有结果-->ret

父子层信息传递需要：

• 数组-->nums
• 这一层是对数组中第几个元素进行判断-->pos

代码逻辑

观察我们想要的结果，都是在叶子结点，很明显，

出口在叶子节点

重复子问题 ：对于每个元素根据其是否存在 ，分两种情况讨论
子问题干啥：存在则将其放入path中，进入下一层，不存在啥也不做，进入下一层

4.2决策树2

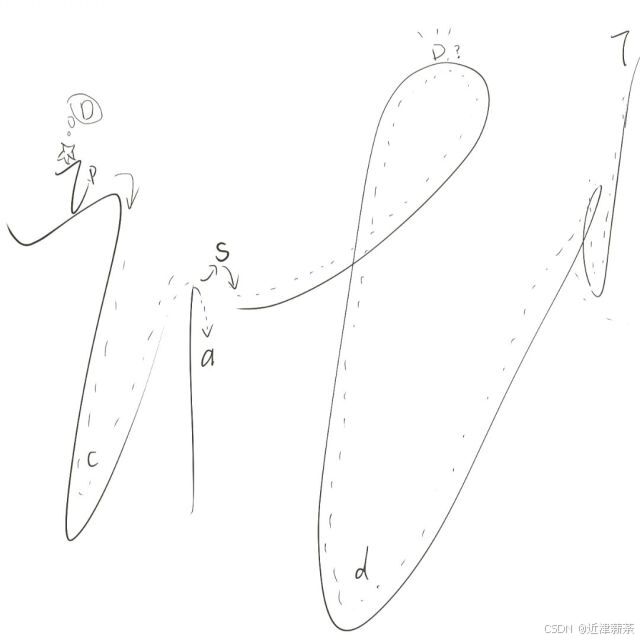
我们也可以根据，子集中元素的个数，来画决策图：

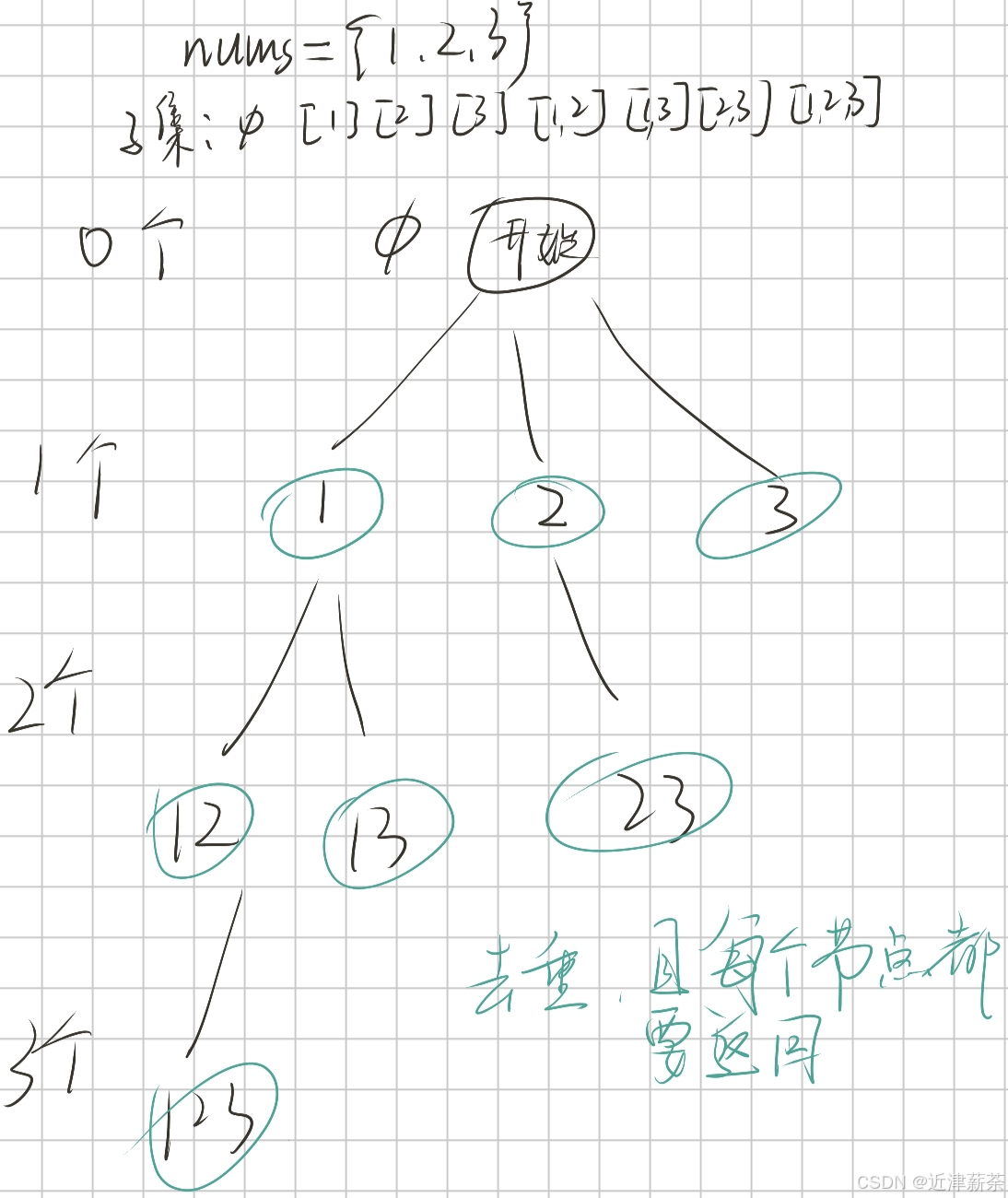
这张决策图同样需要全局变量path和ret，它也能获得我们想要的结果，也是一个好的决策图。

由于子集种没有排序，只有组合，所以我们要对重复的子集进行剪枝 ，如图中所示：按照顺序来给path添加元素

提示:

结合for循环，不用设置return出口，for循环能实现数组递归中的按下标顺序添加元素，进行剪枝，出口的本质是："没有可选择元素"

不知道大家有没有发现，数组往往是多叉树的遍历，多叉树的遍历必然用到for，而for往往是遍历到最后，也就不需要设置return出口~

5.下期要讲解的题目是：

找出所有子集的异或总和再求和

6.嗟食

如果小编写的内容对佬有帮助，还请大佬点点三连加关注哦
佬的支持就是我前进的最大动力 ~

期待与佬的再次相遇~