🔥承渊政道: 个人主页
❄️个人专栏: 《C语言基础语法知识》 《数据结构与算法》
✨逆境不吐心中苦,顺境不忘来时路! 🎬 博主简介:

引言:前篇文章,小编已经介绍了关于C++中多态概念指南与核心内容介绍!相信大家应该有所收获!接下来我将带领大家继续深入学习C++的相关内容!本篇文章着重介绍关于实战全面解析C++二叉搜索树,那么这里面到底有哪些知识需要我们去学习的呢?废话不多说,带着这些疑问,下面跟着小编的节奏🎵一起学习吧!
目录
- 1.⼆叉搜索树的概念
- 2.⼆叉搜索树的性能分析
- 3.⼆叉搜索树的插⼊
- 4.⼆叉搜索树的查找
- 5.⼆叉搜索树的删除
- 6.⼆叉搜索树的实现代码
- 7.⼆叉搜索树key和key/value使⽤场景
- 8.二叉搜索树的相关OJ题
1.⼆叉搜索树的概念
二叉搜索树(Binary Search Tree,简称 BST,也叫二叉查找树),是一种有序的二叉树,它在普通二叉树的基础上,对节点值的分布制定了严格规则:
对树中任意一个节点 node:
①若它的左⼦树不为空,node的左子树中所有节点的值,都小于 node 的值;
②若它的右⼦树不为空,node的右子树中所有节点的值,都大于 node 的值;
③node的左、右子树本身也必须是二叉搜索树(递归定义).
④⼆叉搜索树中可以⽀持插⼊相等的值,也可以不⽀持插⼊相等的值,具体看使⽤场景定义,后续介绍map/set/multimap/multiset系列容器底层就是⼆叉搜索树,其中map/set不⽀持插⼊相等值,multimap/multiset⽀持插⼊相等值.
2.⼆叉搜索树的性能分析
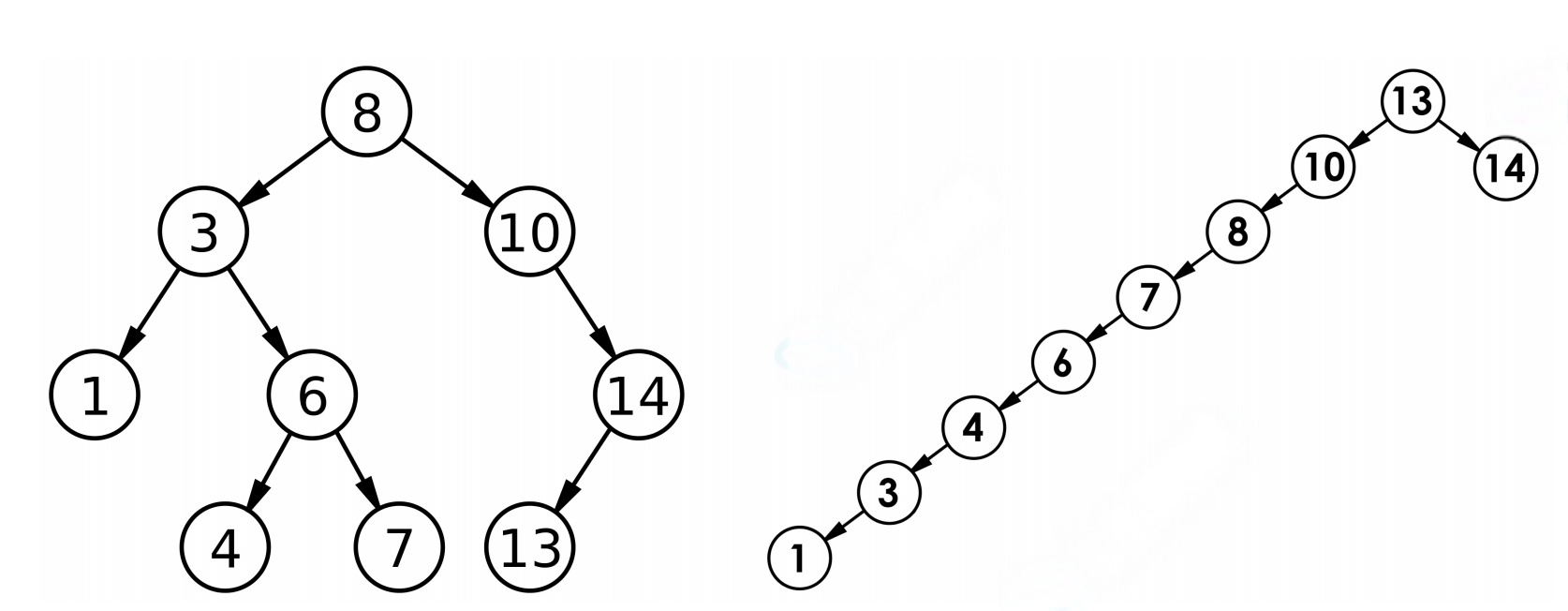
最优情况下,⼆叉搜索树为完全⼆叉树(或者接近完全⼆叉树),其⾼度为:log2N
最差情况下,⼆叉搜索树退化为单⽀树(或者类似单⽀),其⾼度为:N
所以综合⽽⾔⼆叉搜索树增删查改时间复杂度为:O(N)
那么这样的效率显然是⽆法满⾜我们需求的,后续会介绍⼆叉搜索树的变形,平衡⼆叉搜索树AVL树和红⿊树,才能适⽤于我们在内存中存储和搜索数据.另外需要说明的是,⼆分查找也可以实现 O(log2N) 级别的查找效率,但是⼆分查找有两⼤缺陷:
①需要存储在⽀持下标随机访问的结构中,并且有序.
②插⼊和删除数据效率很低,因为存储在下标随机访问的结构中,插⼊和删除数据⼀般需要挪动数据.这⾥也就体现出了平衡⼆叉搜索树的价值.
3.⼆叉搜索树的插⼊
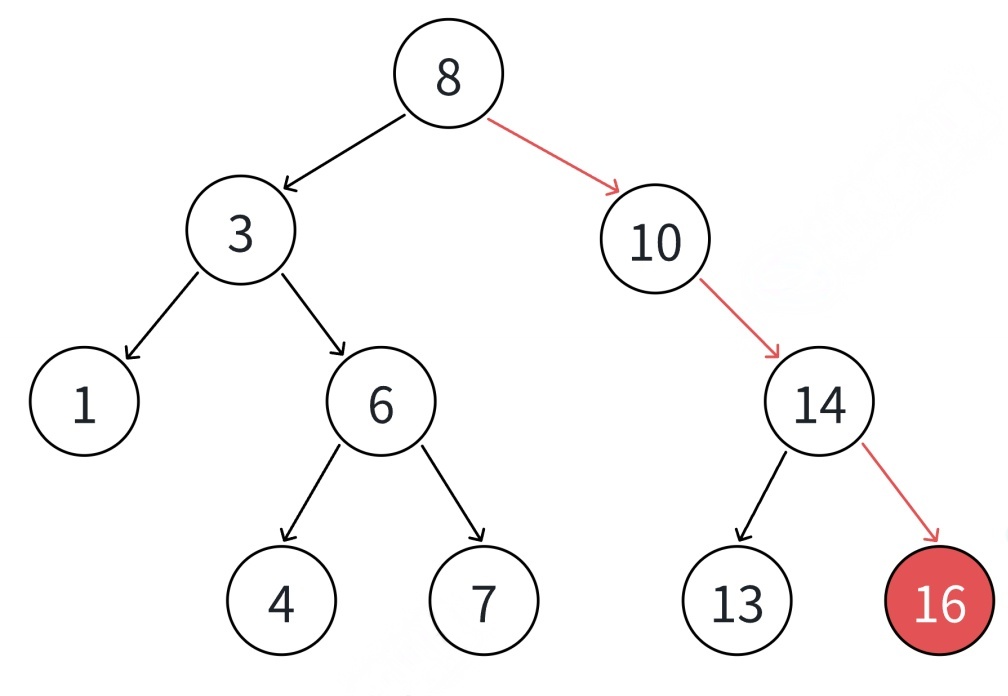
插⼊的具体过程如下:
①树为空,则直接新增结点,赋值给root指针.
②树不空,⼆叉搜索树性质,插⼊值⽐当前结点⼤往右⾛,插⼊值⽐当前结点⼩往左⾛,找到空位置,插⼊新结点.
③如果⽀持插⼊相等的值,插⼊值跟当前结点相等的值可以往右⾛,也可以往左⾛,找到空位置,插⼊新结点.(要注意的是要保持逻辑⼀致性,插⼊相等的值不要⼀会往右⾛,⼀会往左⾛)
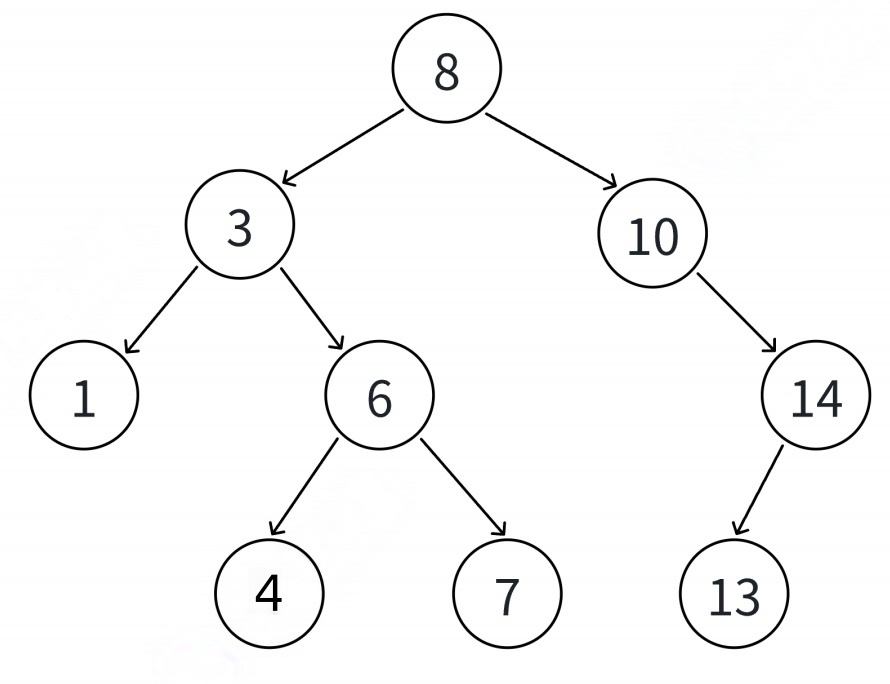
int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};
4.⼆叉搜索树的查找
①从根开始⽐较,查找x,x⽐根的值⼤则往右边⾛查找,x⽐根值⼩则往左边⾛查找.
②最多查找⾼度次,⾛到到空,还没找到,这个值不存在.
③如果不⽀持插⼊相等的值,找到x即可返回.
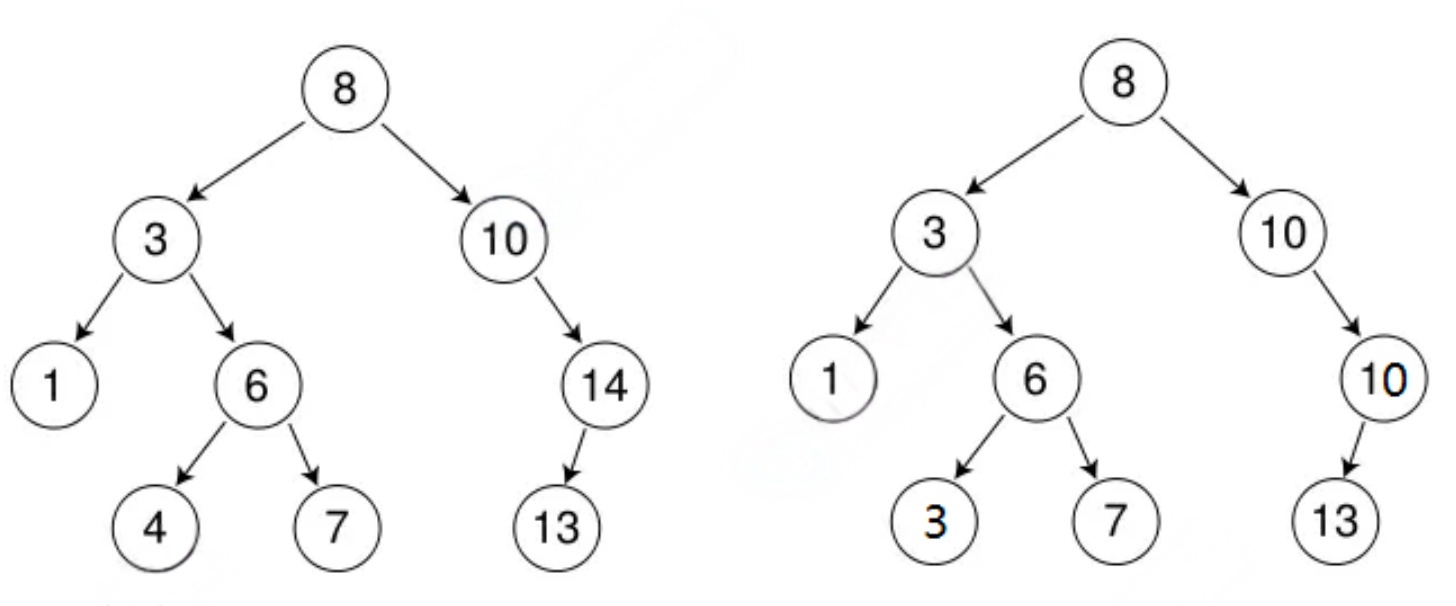
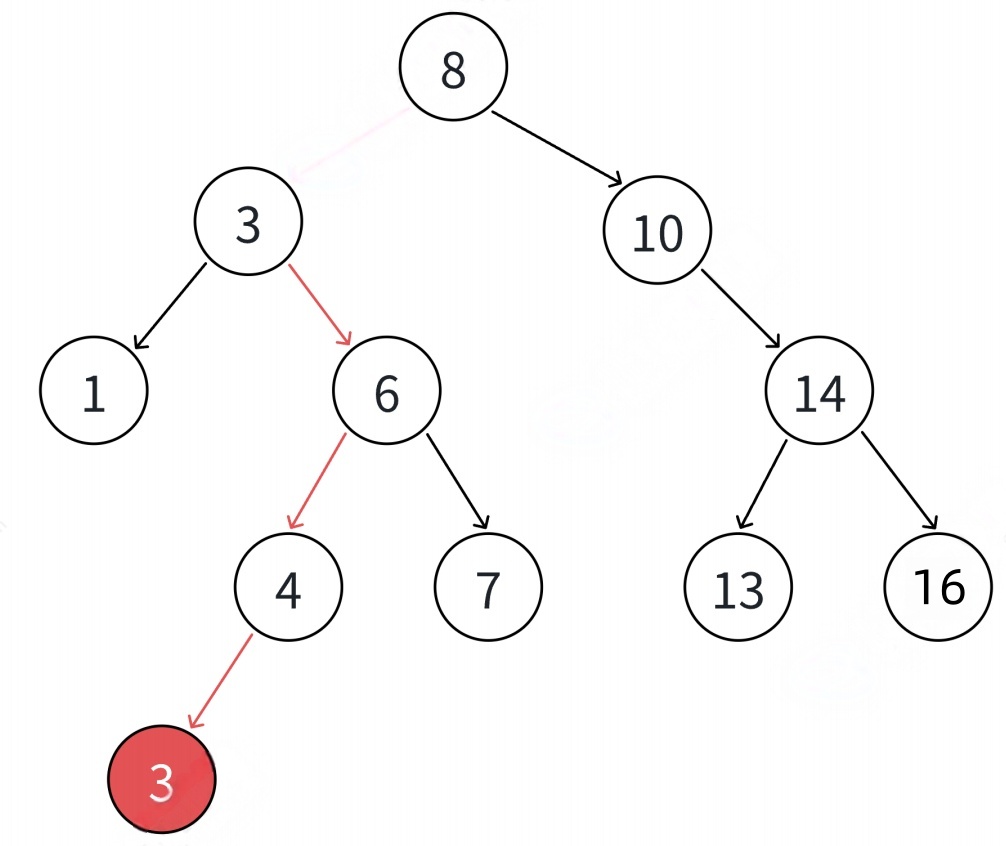
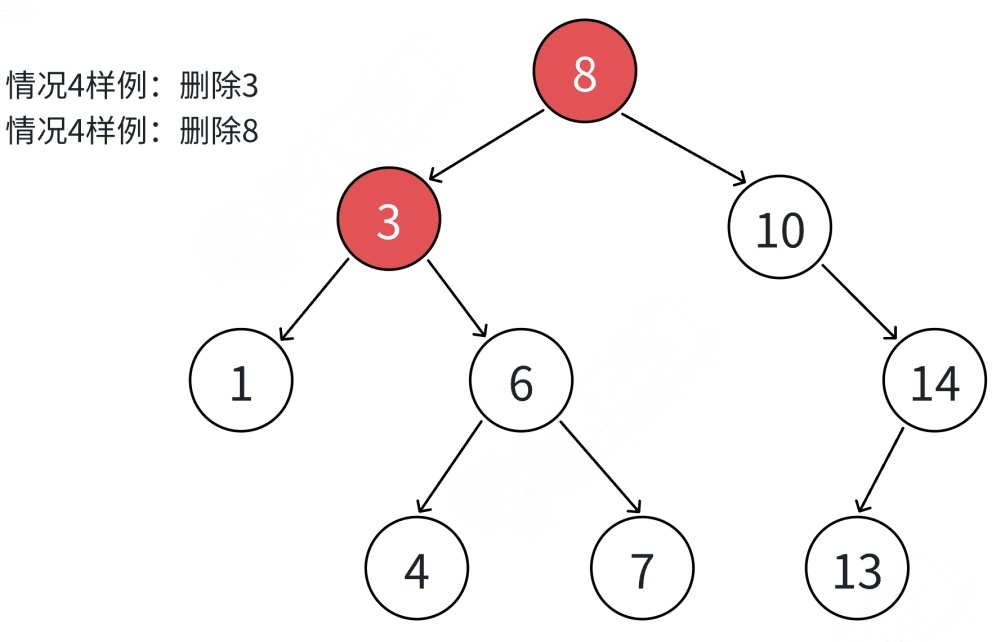
④如果⽀持插⼊相等的值,意味着有多个x存在,⼀般要求查找中序的第⼀个x.如下图,查找3,要找到1的右孩⼦的那个3返回.
5.⼆叉搜索树的删除
⾸先查找元素是否在⼆叉搜索树中,如果不存在,则返回false。
如果查找元素存在则分以下四种情况分别处理:(假设要删除的结点为N)
①要删除结点N左右孩⼦均为空.
②要删除的结点N左孩⼦位空,右孩⼦结点不为空.
③要删除的结点N右孩⼦位空,左孩⼦结点不为空.
④要删除的结点N左右孩⼦结点均不为空.
对应以上四种情况的解决⽅案:
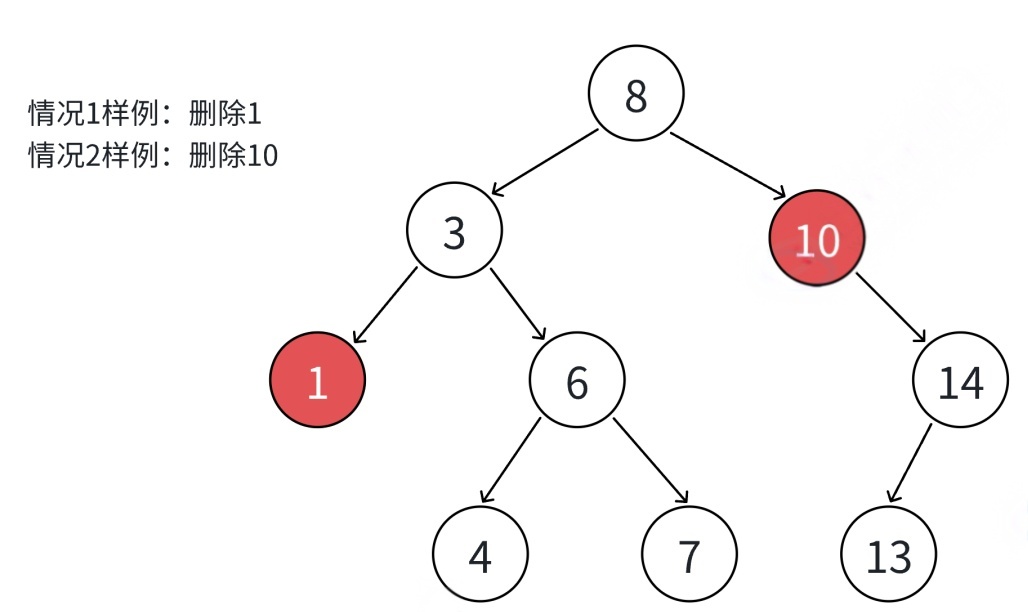
①把N结点的⽗亲对应孩⼦指针指向空,直接删除N结点(情况1可以当成2或者3处理.效果是⼀样的)
②把N结点的⽗亲对应孩⼦指针指向N的右孩⼦,直接删除N结点.
③把N结点的⽗亲对应孩⼦指针指向N的左孩⼦,直接删除N结点.
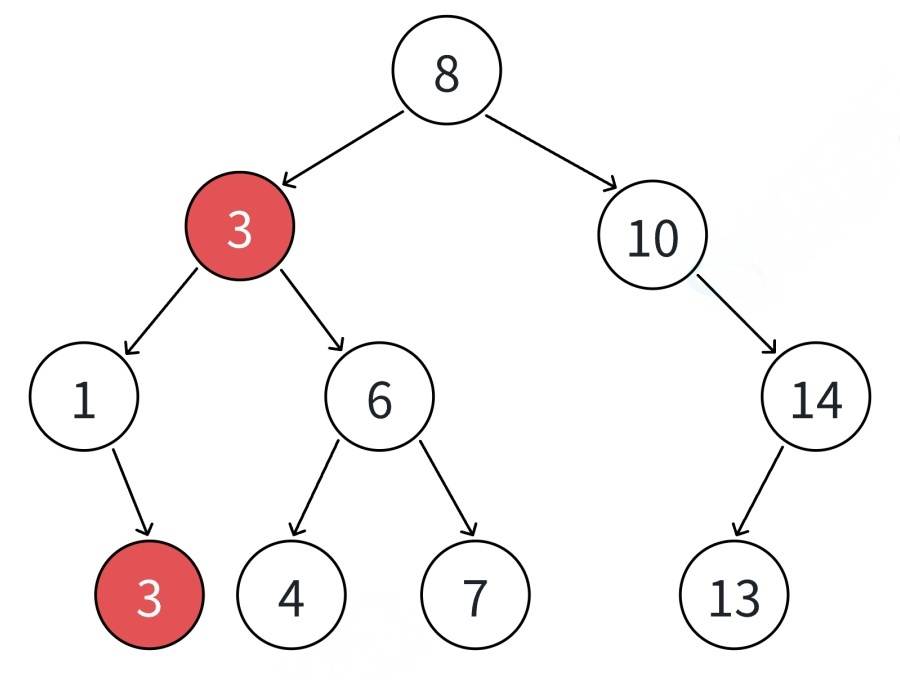
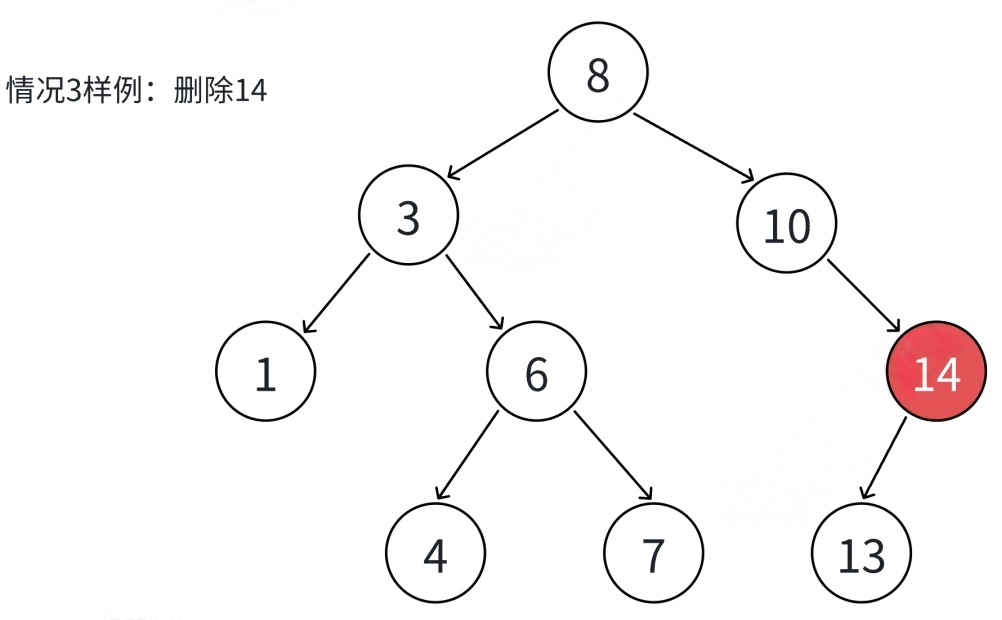
④⽆法直接删除N结点,因为N的两个孩⼦⽆处安放,只能⽤替换法删除.找N左⼦树的值最⼤结点R(最右结点)或者N右⼦树的值最⼩结点R(最左结点)替代N,因为这两个结点中任意⼀个,放到N的位置,都满⾜⼆叉搜索树的规则.替代N的意思就是N和R的两个结点的值交换,转⽽变成删除R结点,R结点符合情况2或情况3,可以直接删除.
6.⼆叉搜索树的实现代码
cpp
#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
using namespace std;
template < class K>
struct BSTNode
{
K _key;
BSTNode<K>*_left;
BSTNode<K>*_right;
BSTNode(const K & key)
:_key(key)
, _left(nullptr)
, _right(nullptr)
{}
};
// Binary Search Tree
template < class K>
class BSTree
{
typedef BSTNode<K> Node;
public:
bool Insert(const K & key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node * parent = nullptr;
Node * cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
bool Find(const K & key)
{
Node * cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
bool Erase(const K & key)
{
Node * parent = nullptr;
Node * cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 0-1个孩⼦的情况
// 删除情况1 2 3均可以直接删除,改变⽗亲对应孩⼦指针指向即可
if (cur->_left == nullptr)
{
if (parent == nullptr)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
parent->_left = cur->_right;
else
parent->_right = cur->_right;
}
delete cur;
return true;
}
else if (cur->_right == nullptr)
{
if (parent == nullptr)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
parent->_left = cur->_left;
else
parent->_right = cur->_left;
}
delete cur;
return true;
}
else
{
// 2个孩⼦的情况
// 删除情况4,替换法删除
// 假设这⾥我们取右⼦树的最⼩结点作为替代结点去删除
// 这⾥尤其要注意右⼦树的根就是最⼩情况的情况的处理,对应课件图中删除8的情况
// ⼀定要把cur给rightMinP,否会报错。
Node * rightMinP = cur;
Node * rightMin = cur->_right;
while (rightMin->_left)
{
rightMinP = rightMin;
rightMin = rightMin->_left;
}
cur->_key = rightMin->_key;
if (rightMinP->_left == rightMin)
rightMinP->_left = rightMin->_right;
else
rightMinP->_right = rightMin->_right;
delete rightMin;
return true;
}
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
private:
void _InOrder(Node * root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
private:
Node * _root = nullptr;
};
int main()
{
int a[] = { 8, 3, 1, 10, 1, 6, 4, 7, 14, 13 };
BSTree<int> t1;
for (auto e : a)
{
t1.Insert(e);
}
t1.InOrder();
t1.Erase(8);
t1.InOrder();
t1.Erase(3);
t1.InOrder();
t1.Erase(14);
t1.InOrder();
t1.Erase(6);
t1.InOrder();
for (auto e : a)
{
t1.Erase(e);
}
t1.InOrder();
return 0;
}7.⼆叉搜索树key和key/value使⽤场景
7.1key搜索场景
只有key作为关键码,结构中只需要存储key即可,关键码即为需要搜索到的值,搜索场景只需要判断key在不在.key的搜索场景实现的⼆叉树搜索树⽀持增删查,但是不⽀持修改,修改key破坏搜索树结构了.
场景1:⼩区⽆⼈值守⻋库,⼩区⻋库买了⻋位的业主⻋才能进⼩区,那么物业会把买了⻋位的业主的⻋牌号录⼊后台系统,⻋辆进⼊时扫描⻋牌在不在系统中,在则抬杆,不在则提示⾮本⼩区⻋辆,⽆法进⼊.
场景2:检查⼀篇英⽂ 章单词拼写是否正确,将词库中所有单词放⼊⼆叉搜索树,读取⽂章中的单词,查找是否在⼆叉搜索树中,不在则波浪线标红提示.
7.2key/value搜索场景
每⼀个关键码key,都有与之对应的值value,value可以任意类型对象.树的结构中(结点)除了需要存储key还要存储对应的value,增/删/查还是以key为关键字⾛⼆叉搜索树的规则进⾏⽐较,可以快速查找到key对应的value.key/value的搜索场景实现的⼆叉树搜索树⽀持修改,但是不⽀持修改key,修改key破坏搜索树性质了,可以修改value.
场景1:简单中英互译字典,树的结构中(结点)存储key(英⽂)和vlaue(中⽂),搜索时输⼊英⽂,则同时
查找到了英⽂对应的中⽂.
场景2:商场⽆⼈值守⻋库,⼊⼝进场时扫描⻋牌,记录⻋牌和⼊场时间,出⼝离场时,扫描⻋牌,查找⼊场时间,⽤当前时间-⼊场时间计算出停⻋时⻓,计算出停⻋费⽤,缴费后抬杆,⻋辆离场.
场景3:统计⼀篇⽂章中单词出现的次数,读取⼀个单词,查找单词是否存在,不存在这个说明第⼀次出现(单词,1),单词存在,则++单词对应的次数.
7.3key/value⼆叉搜索树代码实现
cpp
#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
using namespace std;
template < class K, class V>
struct BSTNode
{
// pair<K, V> _kv;
K _key;
V _value;
BSTNode<K, V>* _left;
BSTNode<K, V>* _right;
BSTNode(const K & key, const V & value)
:_key(key)
, _value(value)
, _left(nullptr)
, _right(nullptr)
{}
};
template < class K, class V>
class BSTree
{
typedef BSTNode<K, V> Node;
public:
BSTree() = default;
BSTree(const BSTree<K, V>&t)
{
_root = Copy(t._root);
}
BSTree<K, V>& operator=(BSTree<K, V> t)
{
swap(_root, t._root);
return *this;
}
~BSTree()
{
Destroy(_root);
_root = nullptr;
}
bool Insert(const K & key, const V & value)
{
if (_root == nullptr)
{
_root = new Node(key, value);
return true;
}
Node * parent = nullptr;
Node * cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key, value);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
Node * Find(const K & key)
{
Node * cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
bool Erase(const K& key)
{
Node * parent = nullptr;
Node * cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
if (cur->_left == nullptr)
{
if (parent == nullptr)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
parent->_left = cur->_right;
else
parent->_right = cur->_right;
}
delete cur;
return true;
}
else if (cur->_right == nullptr)
{
if (parent == nullptr)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
parent->_left = cur->_left;
else
parent->_right = cur->_left;
}
delete cur;
return true;
}
else
{
Node * rightMinP = cur;
Node * rightMin = cur->_right;
while (rightMin->_left)
{
rightMinP = rightMin;
rightMin = rightMin->_left;
}
cur->_key = rightMin->_key;
if (rightMinP->_left == rightMin)
rightMinP->_left = rightMin->_right;
else
rightMinP->_right = rightMin->_right;
delete rightMin;
return true;
}
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
private:
void _InOrder(Node * root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << ":" << root->_value << endl;
_InOrder(root->_right);
}
void Destroy(Node * root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
Node * Copy(Node * root)
{
if (root == nullptr)
return nullptr;
Node * newRoot = new Node(root->_key, root->_value);
newRoot->_left = Copy(root->_left);
newRoot->_right = Copy(root->_right);
return newRoot;
}
private:
Node * _root = nullptr;
};
int main()
{
BSTree<string, string> dict;
//BSTree<string, string> copy = dict;
dict.Insert("left", "左边");
dict.Insert("right", "右边");
dict.Insert("insert", "插⼊");
dict.Insert("string", "字符串");
string str;
while (cin >> str)
{
auto ret = dict.Find(str);
if (ret)
{
cout << "->" << ret->_value << endl;
}
else
{
cout << "⽆此单词,请重新输⼊" << endl;
}
}
return 0;
}
cpp
#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
using namespace std;
template < class K, class V>
struct BSTNode
{
// pair<K, V> _kv;
K _key;
V _value;
BSTNode<K, V>* _left;
BSTNode<K, V>* _right;
BSTNode(const K & key, const V & value)
:_key(key)
, _value(value)
, _left(nullptr)
, _right(nullptr)
{}
};
template < class K, class V>
class BSTree
{
typedef BSTNode<K, V> Node;
public:
BSTree() = default;
BSTree(const BSTree<K, V>&t)
{
_root = Copy(t._root);
}
BSTree<K, V>& operator=(BSTree<K, V> t)
{
swap(_root, t._root);
return *this;
}
~BSTree()
{
Destroy(_root);
_root = nullptr;
}
bool Insert(const K & key, const V & value)
{
if (_root == nullptr)
{
_root = new Node(key, value);
return true;
}
Node * parent = nullptr;
Node * cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key, value);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
Node * Find(const K & key)
{
Node * cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
bool Erase(const K& key)
{
Node * parent = nullptr;
Node * cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
if (cur->_left == nullptr)
{
if (parent == nullptr)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
parent->_left = cur->_right;
else
parent->_right = cur->_right;
}
delete cur;
return true;
}
else if (cur->_right == nullptr)
{
if (parent == nullptr)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
parent->_left = cur->_left;
else
parent->_right = cur->_left;
}
delete cur;
return true;
}
else
{
Node * rightMinP = cur;
Node * rightMin = cur->_right;
while (rightMin->_left)
{
rightMinP = rightMin;
rightMin = rightMin->_left;
}
cur->_key = rightMin->_key;
if (rightMinP->_left == rightMin)
rightMinP->_left = rightMin->_right;
else
rightMinP->_right = rightMin->_right;
delete rightMin;
return true;
}
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
private:
void _InOrder(Node * root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << ":" << root->_value << endl;
_InOrder(root->_right);
}
void Destroy(Node * root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
Node * Copy(Node * root)
{
if (root == nullptr)
return nullptr;
Node * newRoot = new Node(root->_key, root->_value);
newRoot->_left = Copy(root->_left);
newRoot->_right = Copy(root->_right);
return newRoot;
}
private:
Node * _root = nullptr;
};
int main()
{
string arr[] = { "苹果", "西⽠", "苹果", "西⽠", "苹果", "苹果", "西⽠", "苹果", "⾹蕉", "苹果", "⾹蕉" };
BSTree<string, int> countTree;
for (const auto& str : arr)
{
// 先查找⽔果在不在搜索树中
// 1、不在,说明⽔果第⼀次出现,则插⼊<⽔果, 1>
// 2、在,则查找到的结点中⽔果对应的次数++
//BSTreeNode<string, int>* ret = countTree.Find(str);
auto ret = countTree.Find(str);
if (ret == NULL)
{
countTree.Insert(str, 1);
}
else
{
ret->_value++;
}
}
countTree.InOrder();
return 0;
}8.二叉搜索树的相关OJ题
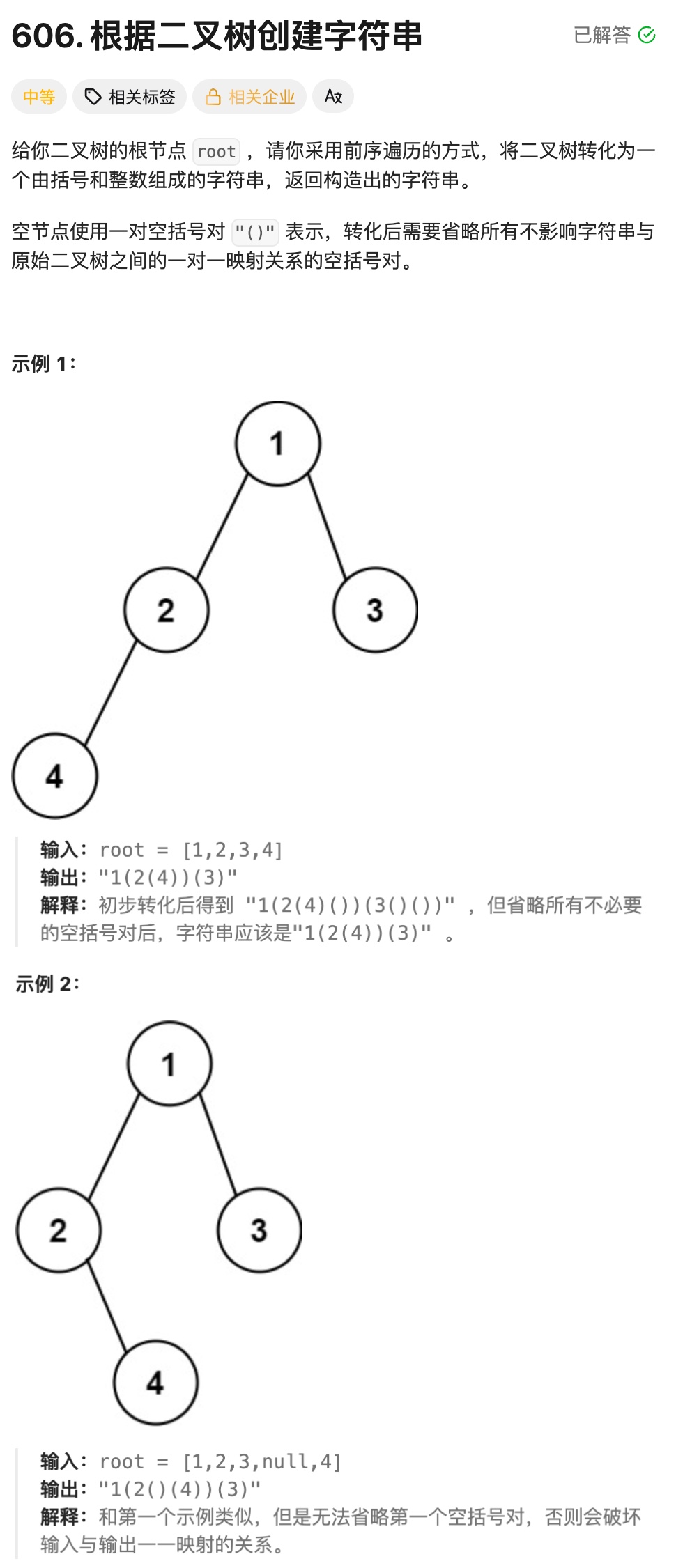
8.1根据二叉树创建字符串
实现思路:
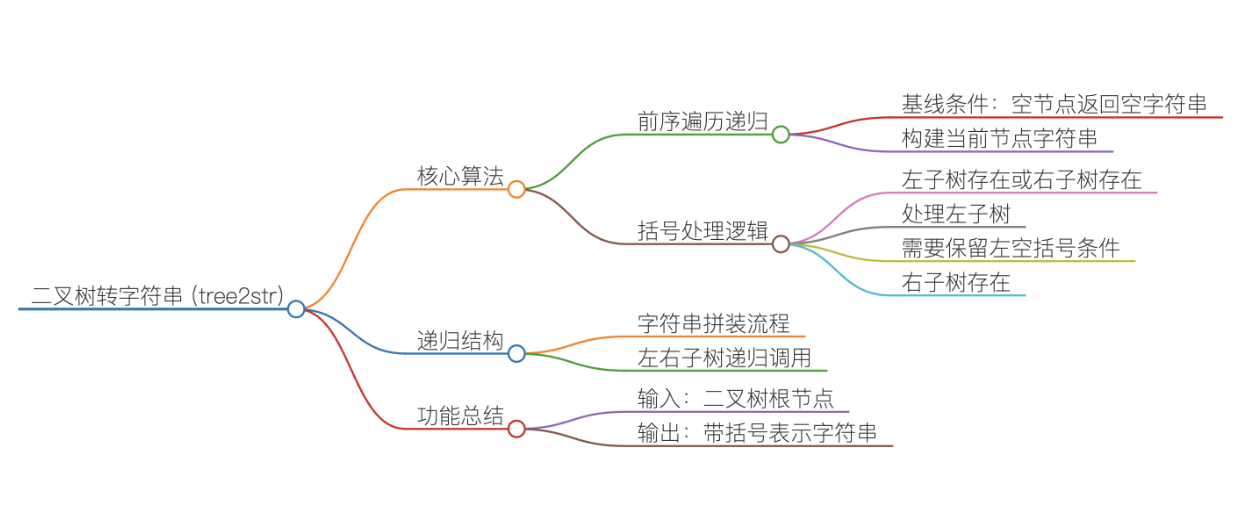
递归终止条件:当节点为空时,直接返回空字符串 "".
当前节点处理:将当前节点的整数值转换为字符串,作为结果的起始部分.
左子树处理:只要左子树非空,或者右子树非空(即使左子树为空),就必须用 () 包裹左子树的递归结果并拼接.这是为了区分 "左子树为空但右子树非空" 的特殊情况,避免二叉树结构产生歧义.
右子树处理:只有当右子树非空时,才用 () 包裹右子树的递归结果并拼接.如果右子树为空,直接省略括号,因为不会影响二叉树的唯一映射关系.
结果返回:将当前节点、左子树(条件性)、右子树(条件性)的字符串拼接后,作为当前子树的结果返回.
cpp
class Solution {
public:
// ⾛前序遍历⼆叉树转换
string tree2str(TreeNode* root) {
if(root == nullptr)
return "";
string ret = to_string(root->val);
//左不为空,需要递归获取子树括号括起来
//左为空,右不为空,左边的空括号需要保留
if(root->left || root->right)
{
ret += '(';
ret += tree2str(root->left);
ret += ')';
}
//右不为空,需要递归获取子树括号括起来
//右边只要是空的,空括号就不需要了
if(root->right)
{
ret += '(';
ret += tree2str(root->right);
ret += ')';
}
return ret;
}
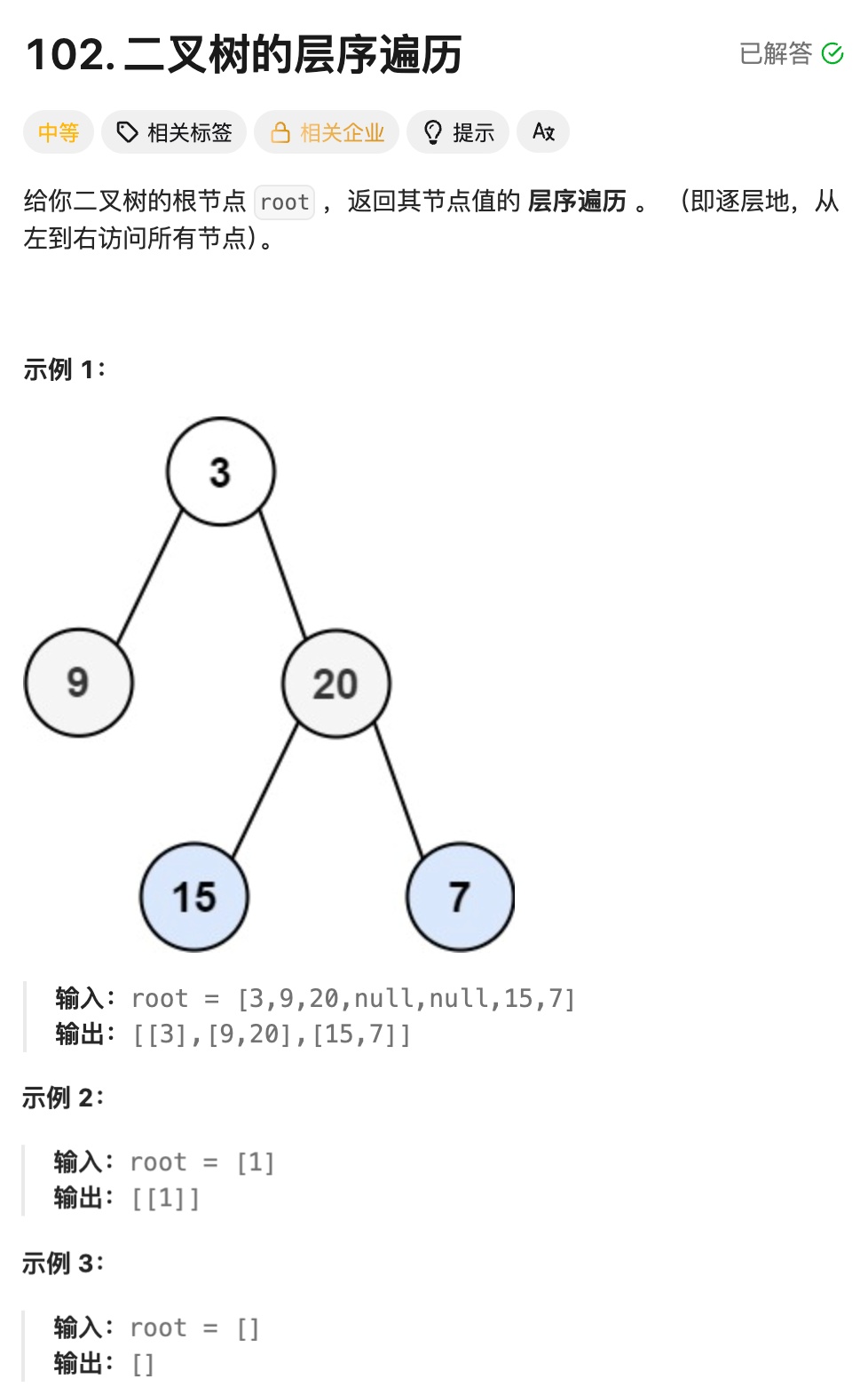
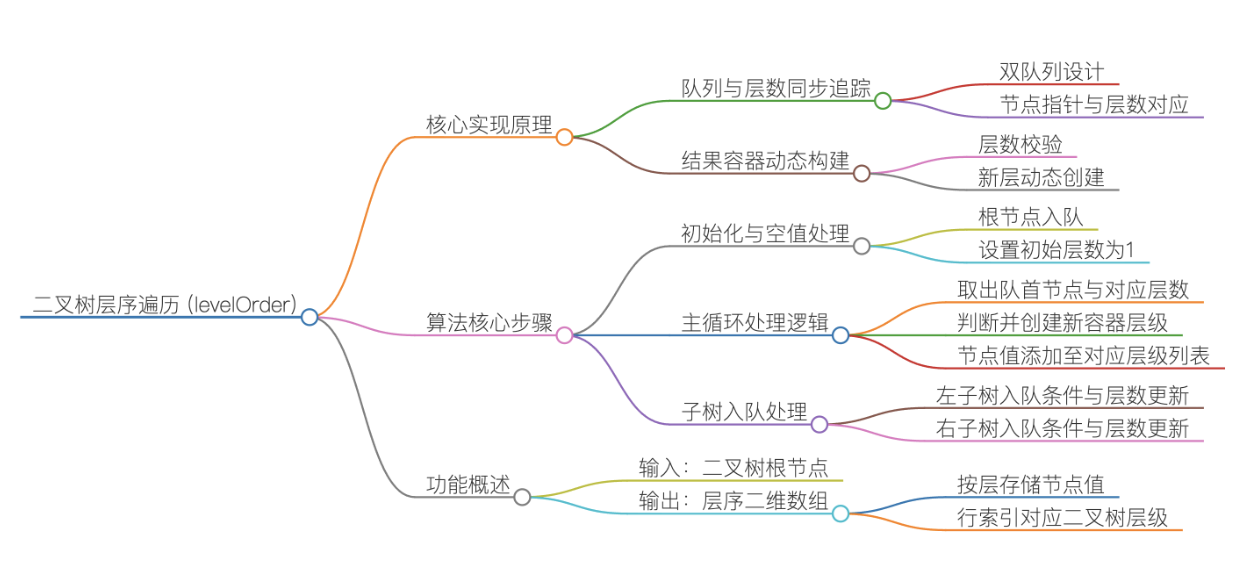
};8.2二叉树的层序遍历
实现思路一:
①初始化与边界处理
先定义最终返回的二维数组 vv,用于按层存储节点值;若根节点 root 为空,直接返回空的 vv(空树无需遍历);
初始化两个队列:
q_node:存储待处理的二叉树节点指针,保证节点按 "层" 的顺序出队;
q_level:存储对应节点的层数(与 q_node 队列一一对应),用于判断节点归属哪一层;
将根节点入 q_node 队列,同时将层数 1 入 q_level 队列(根节点属于第 1 层).
②循环处理队列
只要 q_node 队列不为空(还有节点待处理),就持续执行以下操作:
取出当前节点和层数:分别弹出两个队列的队首元素,得到当前处理的节点 front_node 和其所属层数 current_level;
创建/定位当前层的存储数组:
结果数组 vv 的大小代表 "已处理的层数"(例如 vv.size()=2 说明已处理第 1、2 层);若current_level > vv.size(),说明当前节点属于新的一层,需在 vv 中新增一个空的一维数组,用于存储该层的节点值;
存储当前节点值:将 front_node->val 加入vv[current_level - 1](数组索引从 0 开始,层数从 1 开始,因此减1);
子节点入队:若当前节点有左/右子节点,将子节点入 q_node 队列,同时将 current_level + 1 入 q_level 队列(子节点属于下一层).
③返回结果
当 q_node 队列为空时,所有节点已按层处理完毕,vv 中已按 "第 1 层、第 2 层、......" 的顺序存储了所有节点值,直接返回 vv 即可.
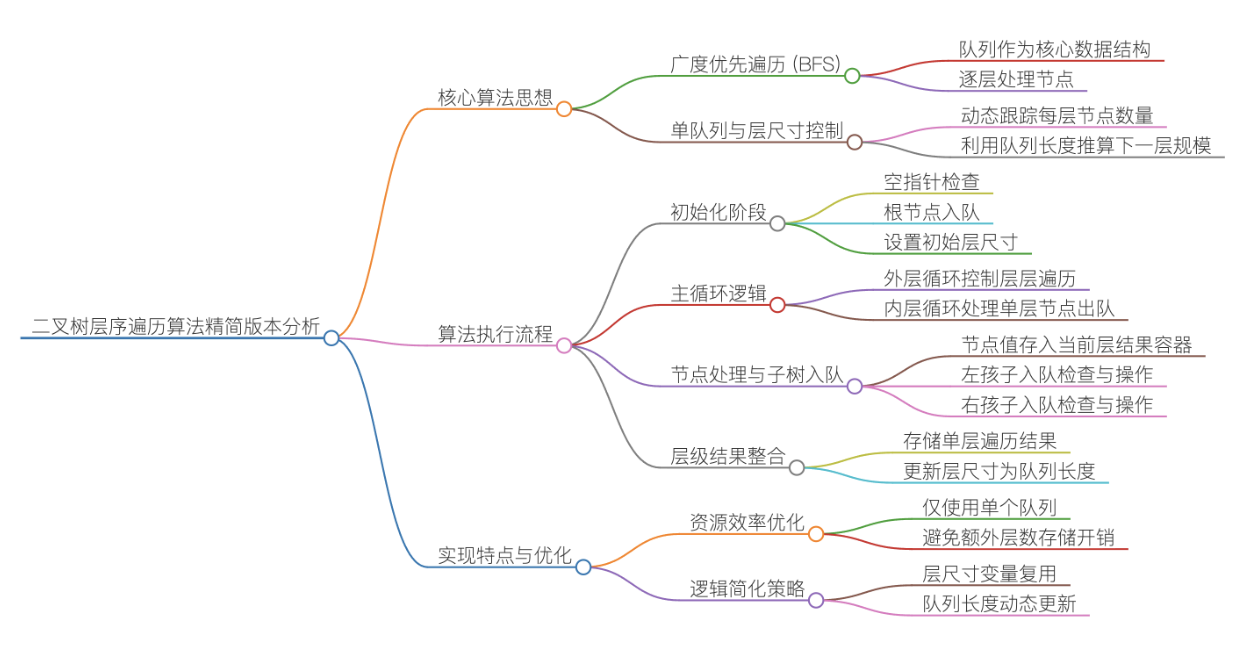
实现思路二:
①初始化与边界处理
定义最终返回的二维数组 vv,用于按层存储节点值;
定义队列 q 存储待处理的二叉树节点指针,定义 levelSize 变量记录当前层待处理的节点数量;
边界判断:若根节点 root 非空,将根节点入队,同时设置 levelSize = 1(根节点是第 1 层,仅有1个节点);若根节点为空,直接返回空的 vv(空树无需遍历).
②核心循环(按层处理节点)
外层循环条件为 levelSize >0(只要当前层还有节点待处理),循环内完成 "处理当前层 + 准备下一层" 核心逻辑:
创建当前层的临时存储数组定义一维数组 v,用于临时存储当前层所有节点的值.
处理当前层的所有节点(内层循环)
内层循环次数由 levelSize 决定(确保只处理当前层节点),每轮执行:
弹出队列队首节点 front;将 front->val 存入临时数组 v;
若 front 有左/右子节点,依次将子节点入队(为下一层处理做准备);
levelSize 自减1,直到当前层所有节点处理完毕(levelSize 变为0).
保存当前层结果将存储了当前层节点值的数组 v 加入最终结果 vv.
更新下一层的节点数当前层节点全部处理完后,队列中恰好存储的是下一层的所有节点,因此将 levelSize 赋值为 q.size()(下一层的节点数量).
③返回结果
当外层循环结束(levelSize变为0,说明所有层都处理完毕),vv 中已按 "第 1 层、第 2 层、......" 的顺序存储了所有节点值,直接返回 vv 即可.
cpp
//思路一的实现
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> vv;
if (root == nullptr) {
return vv;
}
// 双队列:一个存节点指针,一个存对应节点的层数
queue<TreeNode*> q_node;
queue<int> q_level;
// 初始化:根节点入队,层数为1
q_node.push(root);
q_level.push(1);
while (!q_node.empty()) {
// 取出队首节点和对应的层数
TreeNode* front_node = q_node.front();
int current_level = q_level.front();
q_node.pop();
q_level.pop();
// 如果当前层数超过结果容器的大小,说明需要新增一层
if (current_level > vv.size()) {
vv.push_back(vector<int>());
}
// 将节点值加入对应层的结果列表
vv[current_level - 1].push_back(front_node->val);
// 左孩子入队,层数+1
if (front_node->left != nullptr) {
q_node.push(front_node->left);
q_level.push(current_level + 1);
}
// 右孩子入队,层数+1
if (front_node->right != nullptr) {
q_node.push(front_node->right);
q_level.push(current_level + 1);
}
}
return vv;
}
};
cpp
//思路二的实现
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> vv;
queue<TreeNode*> q;
int levelSize = 0;
if(root)
{
q.push(root);
levelSize = 1;
}
while(levelSize > 0)
{
// 一层一层出
vector<int> v;
while(levelSize--)
{
TreeNode* front = q.front();
q.pop();
v.push_back(front->val);
// 下一层孩子入队列
if(front->left)
q.push(front->left);
if(front->right)
q.push(front->right);
}
vv.push_back(v);
// 当前层出完了,下一层都进队列了
// q.size()就是下一层的节点个数
levelSize = q.size();
}
return vv;
}
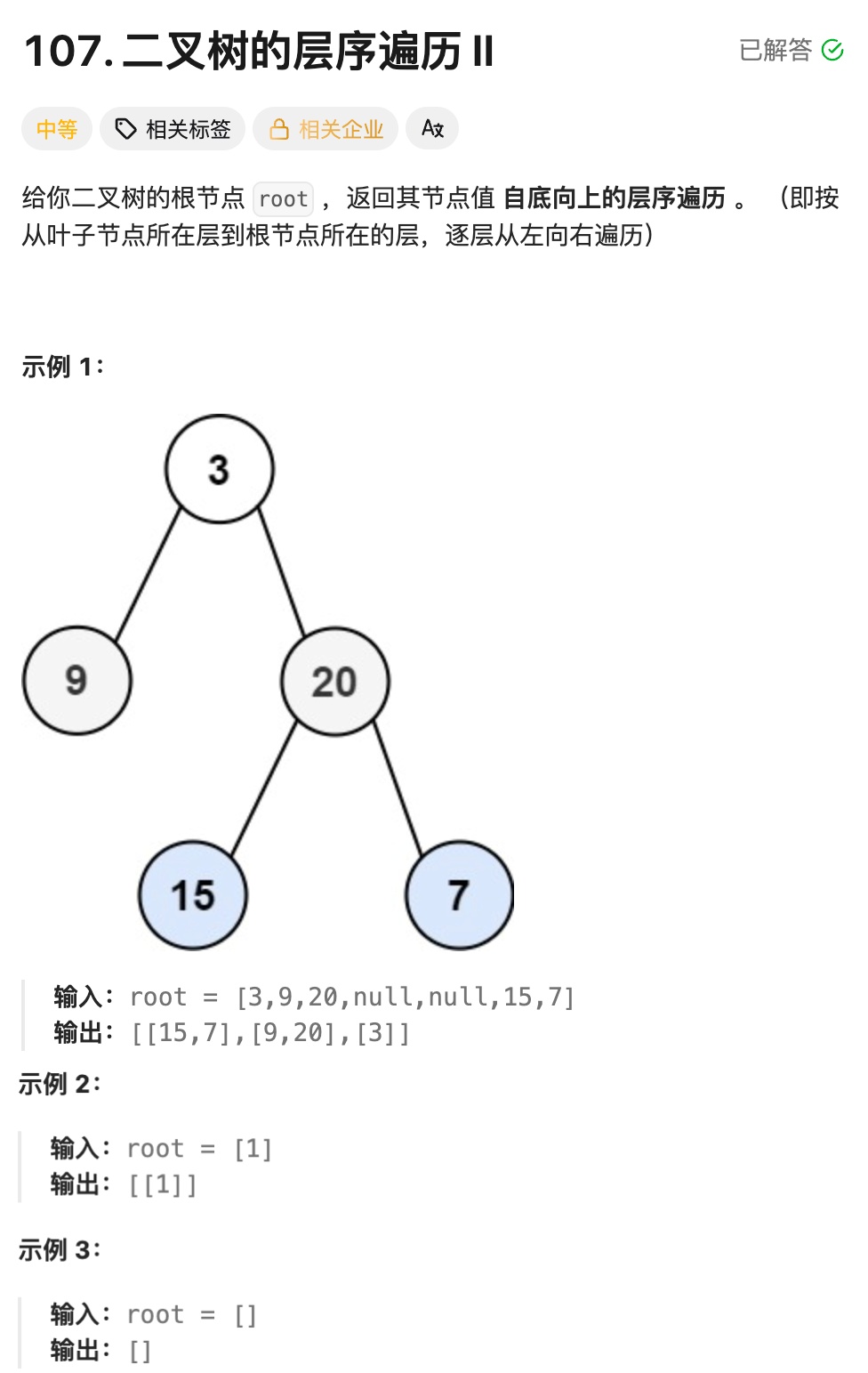
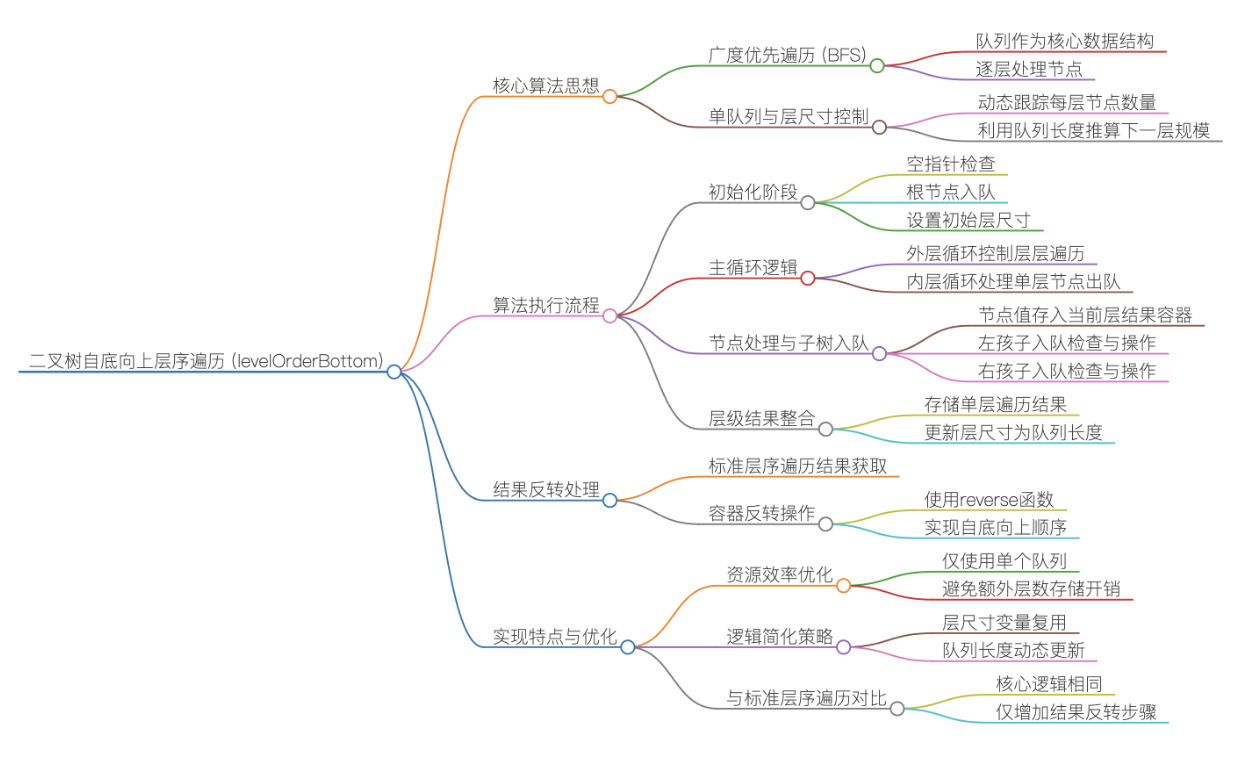
};8.3二叉树的层序遍历||
实现思路:
①初始化与边界处理
定义最终返回的二维数组 vv,用于先存储 "从上到下" 的层序遍历结果;定义队列q存储待处理的二叉树节点指针,定义 levelSize 变量记录当前层待处理的节点数量;
边界判断:若根节点 root 非空,将根节点入队,同时设置 levelSize =1(根节点是第 1 层,仅有 1 个节点);若根节点为空,直接返回空的 vv(空树无需遍历).
②核心循环(从上到下的层序遍历)
这一步和普通的层序遍历逻辑完全一致,通过 levelSize 控制 "按层处理节点":
外层循环条件为levelSize >0(当前层还有节点待处理);
内层循环按 levelSize 次数处理当前层所有节点:弹出队首节点,将节点值存入临时数组 v,并将节点的左右子节点入队(为下一层做准备);
每处理完一层,将临时数组v加入 vv(此时 vv 中是 "第 1 层、第 2 层、......、最后一层" 的顺序);
更新 levelSize 为队列大小(即下一层的节点数),继续循环直到所有层处理完毕.
③反转结果数组(核心差异点)
当 "从上到下" 的层序遍历完成后,vv 中存储的是 "根节点层 → 叶子节点层" 的顺序,此时调用reverse(vv.begin(), vv.end()) 反转整个二维数组,将顺序改为 "叶子节点层 → 根节点层",实现自底向上的效果.
④返回结果
返回反转后的 vv,即为二叉树自底向上的层序遍历结果.
cpp
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> vv;
queue<TreeNode*> q;
int levelSize = 0;
if(root)
{
q.push(root);
levelSize = 1;
}
while(levelSize > 0)
{
// 一层一层出
vector<int> v;
while(levelSize--)
{
TreeNode* front = q.front();
q.pop();
v.push_back(front->val);
// 下一层孩子入队列
if(front->left)
q.push(front->left);
if(front->right)
q.push(front->right);
}
vv.push_back(v);
// 当前层出完了,下一层都进队列了
// q.size()就是下一层的节点个数
levelSize = q.size();
}
reverse(vv.begin(),vv.end());
return vv;
}
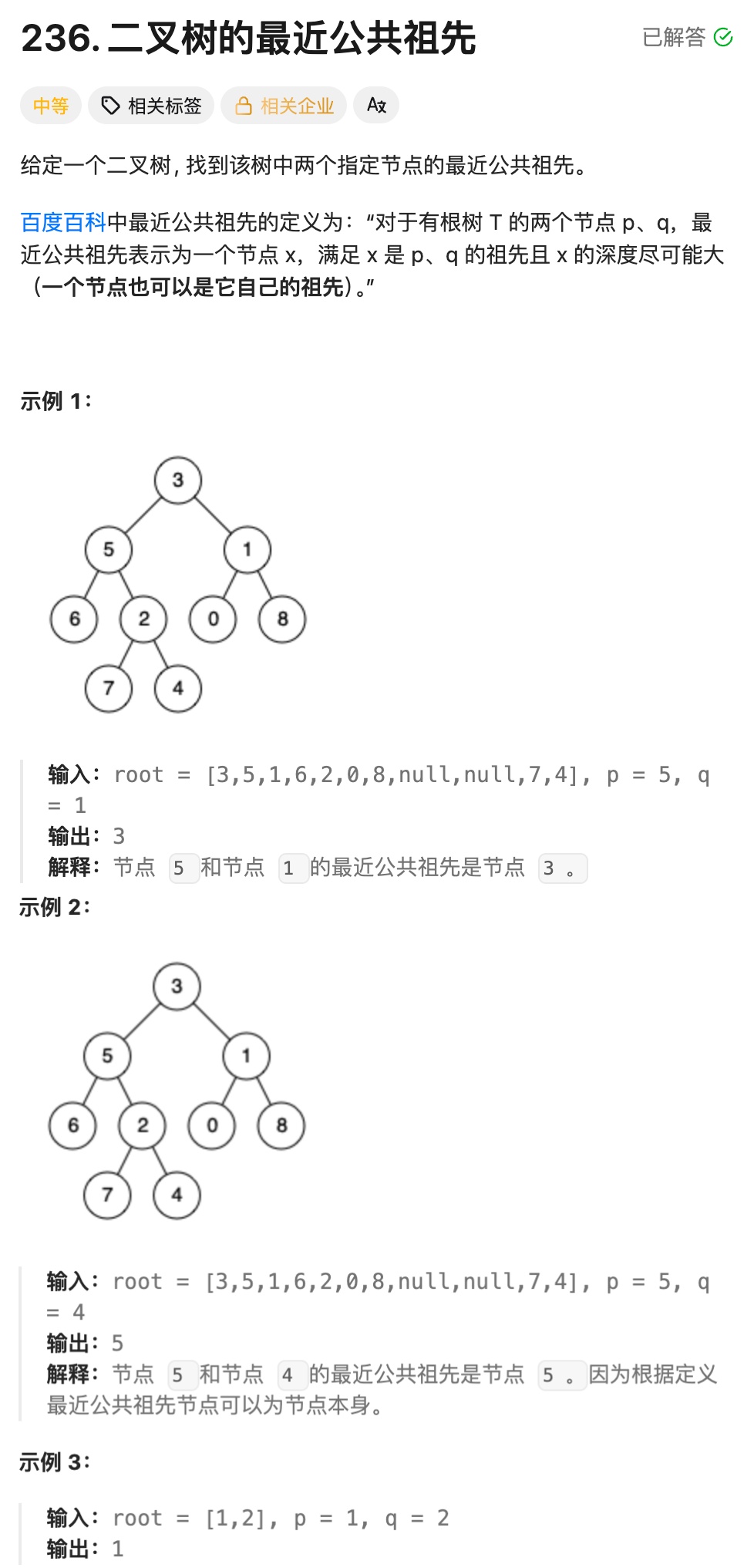
};8.4二叉树的最近公共祖先
实现思路一:
①辅助函数:IsInTree(判断节点是否在子树中)
该函数是核心工具,用于判断目标节点 x 是否存在于以 t 为根的子树中:
终止条件:如果当前节点 t 为空,直接返回 false(空树不可能包含任何节点);
递归逻辑:若当前节点 t 就是目标节点 x,返回 true;否则递归检查 t 的左子树、右子树,只要任一子树包含 x,就返回 true;只有左、右子树都不包含 x 时,才返回 false.
②主函数:lowestCommonAncestor(查找最近公共祖先)
边界/终止条件处理:若根节点 root 为空,返回 nullptr(空树无公共祖先);若root 本身就是p或q,直接返回 root(因为当前节点是其中一个目标节点,它就是自身与另一个节点的公共祖先).
判断 p/q 在当前根节点的子树归属:调用 IsInTree 判断 p 是否在 root 的左子树(pInLeft),则pInRight = !pInLeft(不在左子树就一定在右子树,题目默认 p/q 必在树中);同理,判断 q 是否在 root 的左子树(qInLeft),则 qInRight = !qInLeft.
分情况递归查找公共祖先:根据 p/q 的归属位置,分 3 种情况处理(核心逻辑)
情况1:p和q分别在 root 的左、右子树(pInLeft&&qInRight 或 qInLeft&&pInRight)→ 当前 root 就是最近公共祖先(再往下递归,无法找到同时包含 p/q 的节点);
情况2:p和q都在 root 的左子树(pInLeft&&qInLeft)→ 递归到 root->left 继续查找;
情况3:p和q都在 root 的右子树→递归到 root->right 继续查找.
③返回结果
递归会持续缩小查找范围,直到找到满足 "p/q 分属左右子树" 或 "当前节点是 p/q" 的节点,该节点即为p和q的最近公共祖先.
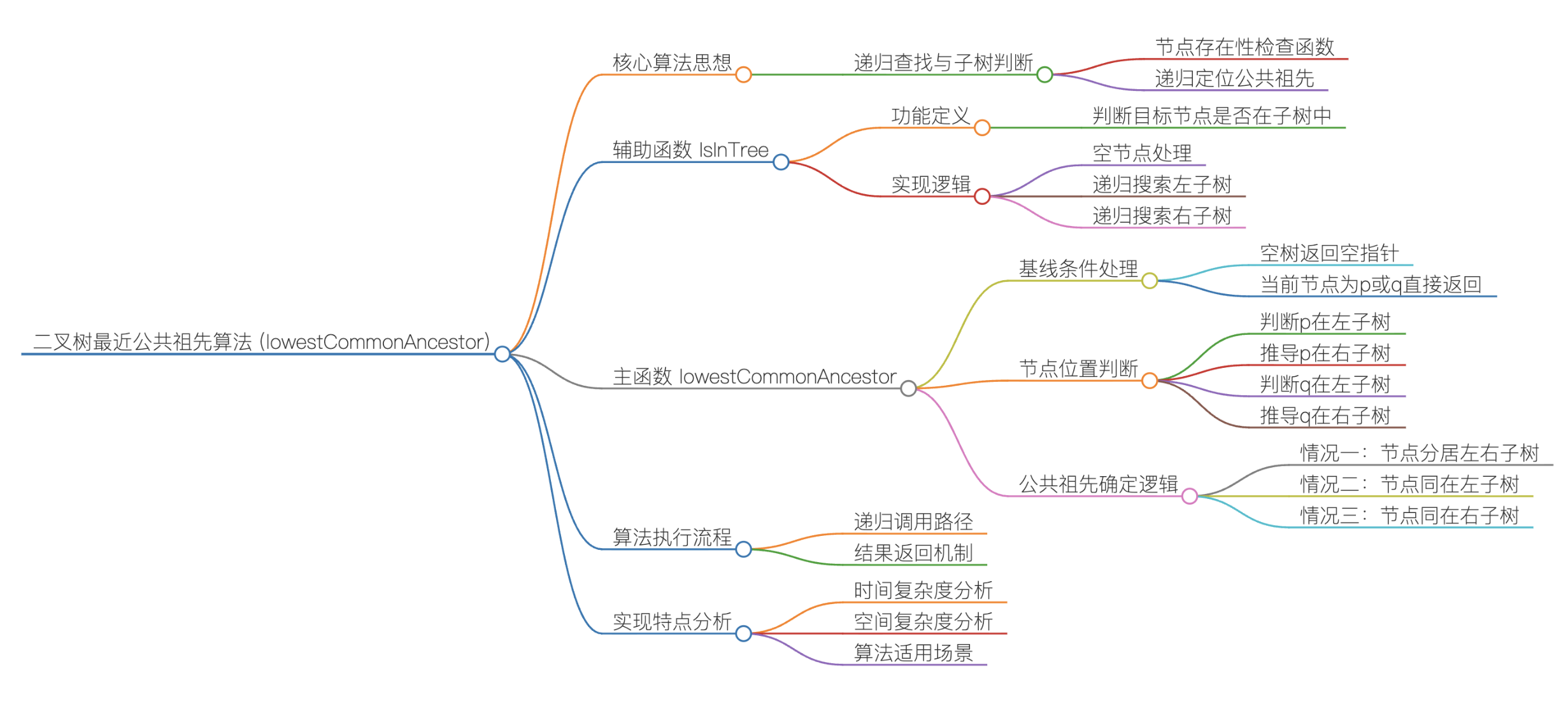
实现思路二:
①辅助函数:GetPath(获取根到目标节点的路径)
该函数通过前序深度优先遍历(DFS)+栈回溯,记录从根节点到目标节点 x 的完整路径:
终止条件:若当前节点 root 为空,返回 false(空树无法找到目标节点);
入栈操作:将当前节点 root 压入路径栈 path(前序遍历的 "访问当前节点" 步骤);
匹配目标节点:若当前节点 root 就是目标节点 x,返回 true(找到路径,无需继续递归);
递归查找子树:先递归查找左子树,若左子树找到 x(返回 true),直接向上返回 true;
左子树没找到则递归查找右子树,若右子树找到x(返回 true),直接向上返回 true;
回溯操作:若左、右子树都没找到 x,说明当前节点不在根到 x 的路径上,将其从栈中弹出(回溯),并返回 false.
②主函数:lowestCommonAncestor(找路径的最近公共交点)
获取两条目标路径:定义两个栈 pPath、qPath,分别调用 GetPath 函数,获取根节点到 p、根节点到 q 的完整路径栈(栈底是根节点,栈顶是目标节点).
对齐两条路径的长度:由于 p/q 可能在不同深度,先让较长的路径栈弹出栈顶节点,直到两个栈的长度相同(确保从同一深度开始比对):
若pPath更长,弹出 pPath 的栈顶; 若qPath更长,弹出 qPath 的栈顶;循环直到pPath.size() == qPath.size().
逐节点比对找公共祖先:从对齐后的深度开始,同时弹出两个栈的栈顶节点,直到找到第一个相同的节点(该节点就是两条路径的最后一个公共节点,即最近公共祖先):若栈顶节点不同,同时弹出两个栈的栈顶;
若栈顶节点相同,该节点即为最近公共祖先,直接返回.
③返回结果
返回找到的公共节点,即为p和q的最近公共祖先.
cpp
//思路一
class Solution {
public:
bool IsInTree(TreeNode* t, TreeNode* x)
{
if(t == nullptr)
return false;
return t == x
|| IsInTree(t->left, x)
|| IsInTree(t->right, x);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
if(root == nullptr)
return nullptr;
if(root == p || root == q)
{
return root;
}
bool pInLeft = IsInTree(root->left, p);
bool pInRight = !pInLeft;
bool qInLeft = IsInTree(root->left, q);
bool qInRight = !qInLeft;
// 1、p和q分别在左和右,root就是最近公共祖先
// 2、p和q都在左,递归到左子树查找
// 3、p和q都在右,递归到右子树查找
if((pInLeft && qInRight) || (qInLeft && pInRight))
{
return root;
}
else if(pInLeft && qInLeft)
{
return lowestCommonAncestor(root->left, p, q);
}
else
{
return lowestCommonAncestor(root->right, p, q);
}
}
};
cpp
//思路二
class Solution {
public:
bool GetPath(TreeNode* root, TreeNode* x, stack<TreeNode*>& path)
{
// 深度遍历前序查找,顺便用栈记录路径
if(root == nullptr)
return false;
path.push(root);
if(root == x)
return true;
if(GetPath(root->left, x, path))
return true;
if(GetPath(root->right, x, path))
return true;
path.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
stack<TreeNode*> pPath, qPath;
GetPath(root, p, pPath);
GetPath(root, q, qPath);
// 找交点
while(pPath.size() != qPath.size())
{
// 长的先走
if(pPath.size() > qPath.size())
{
pPath.pop();
}
else
{
qPath.pop();
}
}
// 再同时走找交点
while(pPath.top() != qPath.top())
{
pPath.pop();
qPath.pop();
}
return pPath.top();
}
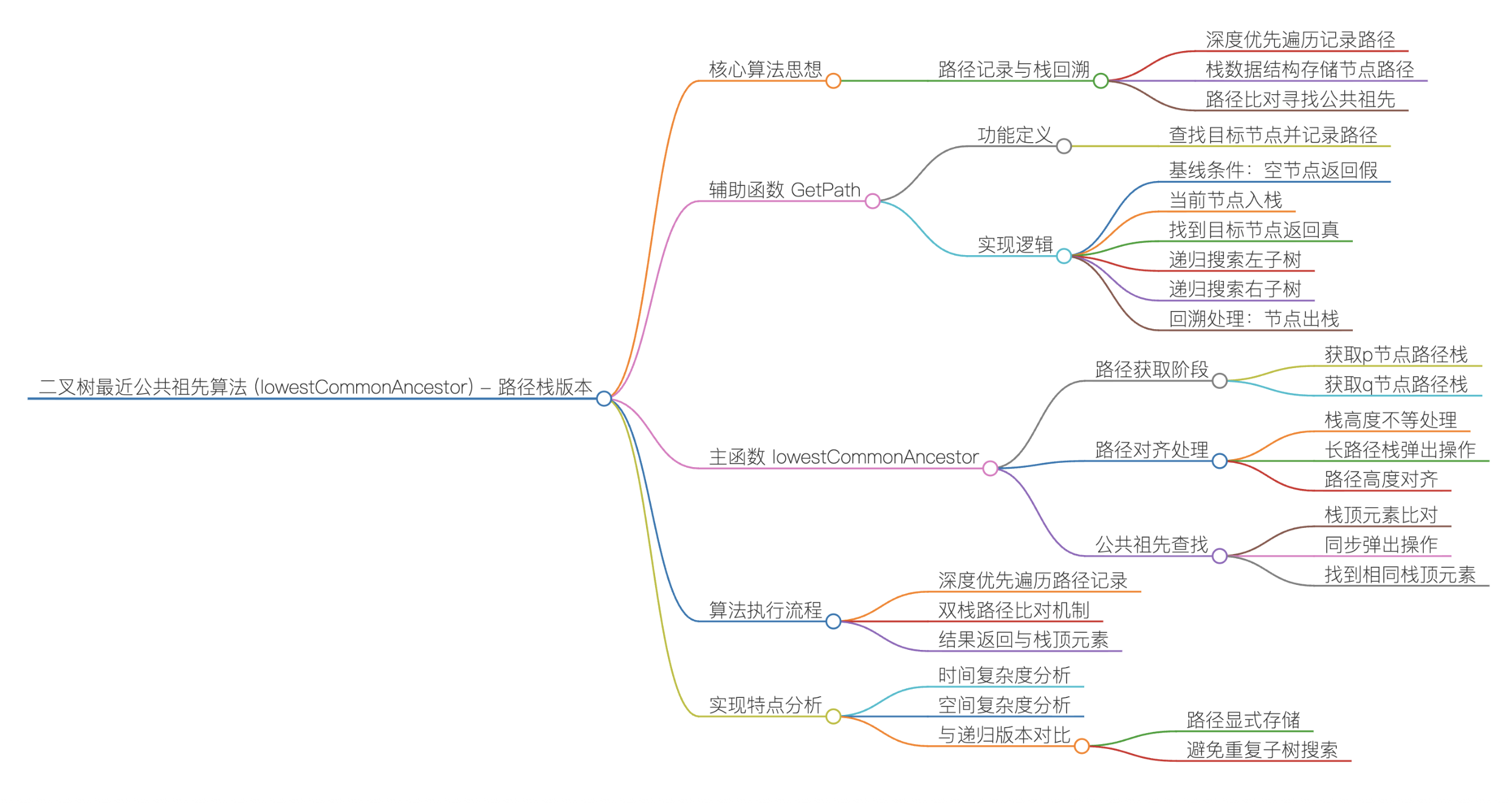
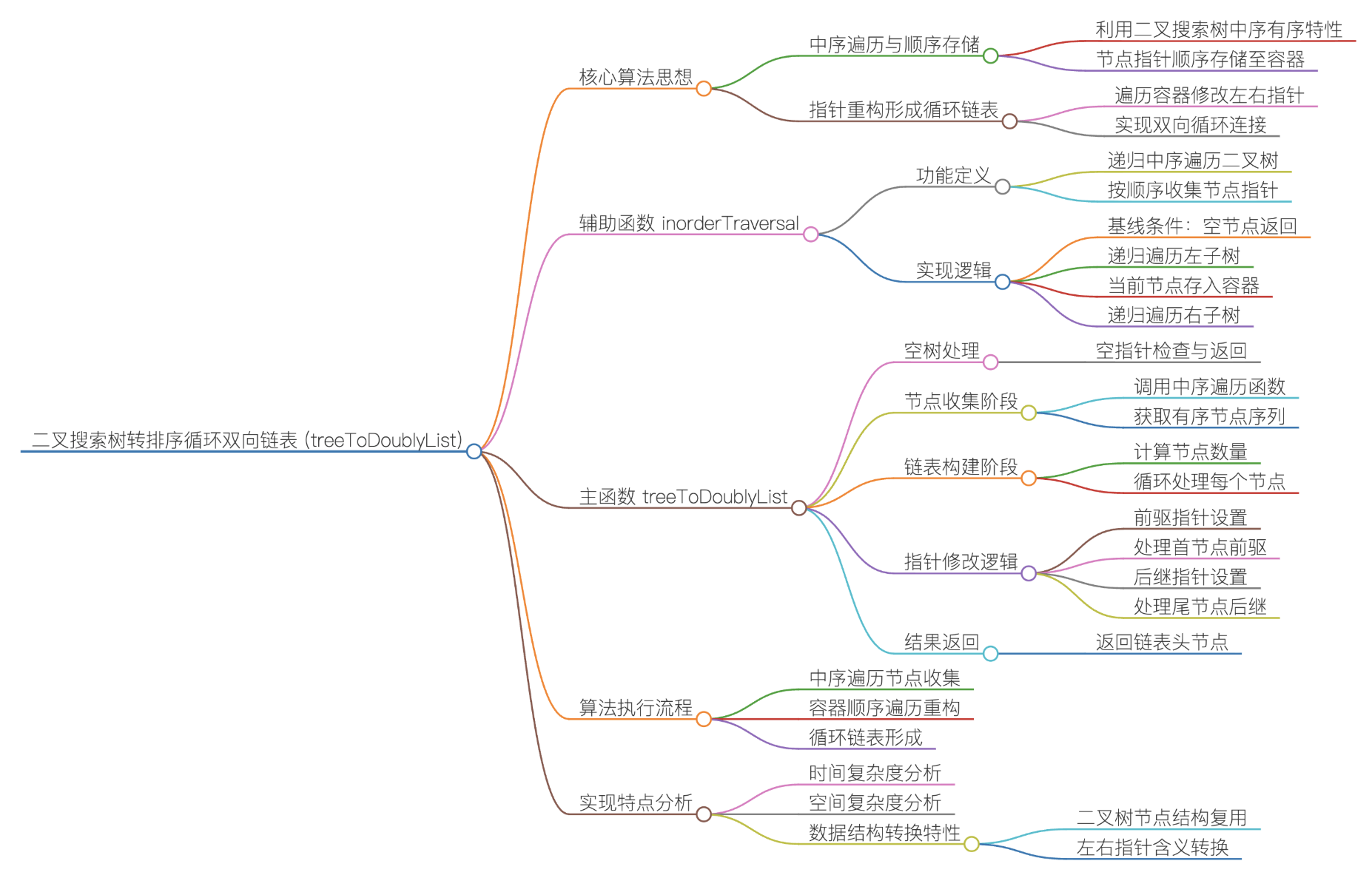
};8.5将二叉搜索树转化为排序的双向链表
实现思路一:
①边界条件处理
如果输入的根节点root 为空(空树),直接返回 nullptr,无需后续处理.
②中序遍历收集节点(核心前提)
定义辅助函数 inorderTraversal,通过递归中序遍历(左子树 → 根节点 → 右子树)遍历 BST:
终止条件:当前节点为空时,直接返回;
遍历逻辑:先递归遍历左子树,再将当前节点存入 vector<Node*> 数组 nodes,最后递归遍历右子树;
关键特性:BST 的中序遍历结果是严格升序的,这保证了 nodes 数组中的节点天然是链表需要的有序序列.
③重构循环双向链表的指针
遍历存储节点的 nodes 数组,为每个节点重新设置 left(前驱)和 right(后继)指针,实现 "双向 + 循环":
先获取节点总数n;对每个索引 i 的节点:
前驱指针(left):指向(i - 1 + n) % n 位置的节点(+n 避免负数,%n 实现循环 ------ 第一个节点的前驱是最后一个节点);
后继指针(right):指向(i + 1)%n位置的节点(%n 实现循环 ------ 最后一个节点的后继是第一个节点);
例如:
索引0(第一个节点):left → 索引n-1(最后一个节点),right → 索引1;
索引n-1(最后一个节点):left →索引n-2,right → 索引0.
④返回结果
返回 nodes[0](即中序遍历的第一个节点,对应 BST 的最小值节点),作为循环双向链表的起始节点.
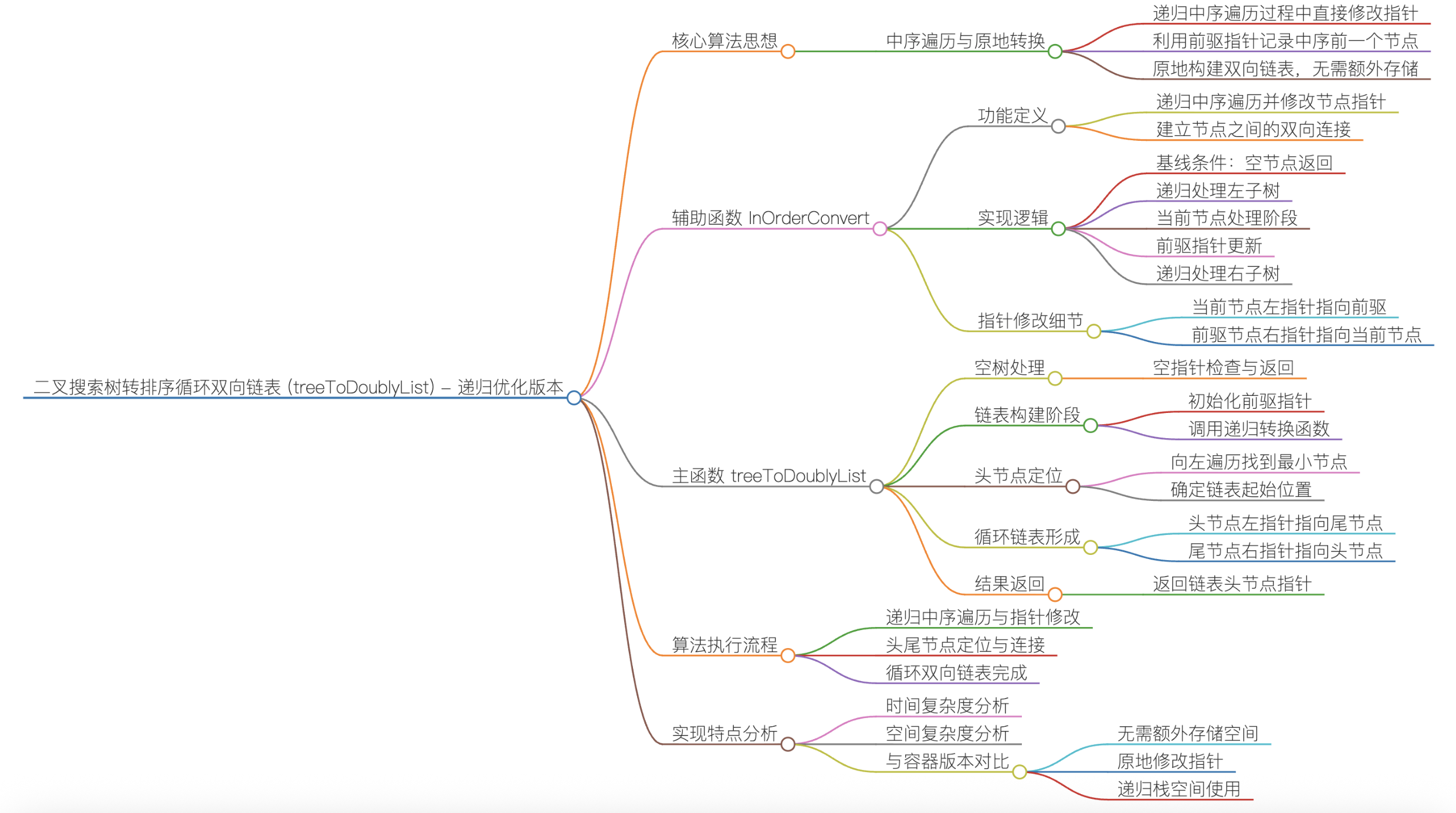
实现思路二:
①辅助函数:InOrderConvert(中序遍历 + 原地修改指针)
该函数通过递归中序遍历,借助引用传递的 prev 指针(跟踪中序遍历的上一个节点),原地修改节点的左右指针(左 = 前驱、右 = 后继):
终止条件:当前节点 cur 为空,直接返回(空节点无需处理);
递归左子树:先递归处理 cur 的左子树,保证遍历顺序是 "左→根→右"(BST 中序遍历为升序);
核心:修改双向指针将cur 的左指针指向 prev(让左指针成为双向链表的 "前驱");
若prev 不为空(说明不是第一个节点),将 prev 的右指针指向 cur(让 prev 的右指针成为 "后继");
更新 prev 为当前节点 cur,为下一个节点的处理做准备;
递归右子树:处理 cur 的右子树,继续按升序构建链表.
②主函数:treeToDoublyList(初始化 + 找头节点 + 构建循环)
边界处理:若根节点 root 为空,直接返回 nullptr(空树无法构建链表).
初始化并执行中序转换:定义前驱指针 prev 并初始化为 nullptr;
调用 InOrderConvert(root, prev),完成所有节点的双向指针修改(此时链表已按升序连接,但未形成循环).
找链表的头节点:BST 的中序遍历第一个节点是最左节点(最小值),因此从 root 出发,不断向左遍历(head = head->left),直到 head->left 为空,该节点即为链表头节点 head.
构建循环链表:中序遍历的最后一个节点是 prev(最右节点,最大值),将首尾节点互相指向完成循环:
头节点 head 的左指针指向尾节点 prev;尾节点 prev 的右指针指向头节点 head.
③返回结果
返回链表头节点 head(升序链表的第一个节点).
cpp
//思路一
class Solution {
public:
Node* treeToDoublyList(Node* root) {
if (root == nullptr) {
return nullptr;
}
vector<Node*> nodes;
// 中序遍历,将节点按升序存入vector
inorderTraversal(root, nodes);
int n = nodes.size();
// 修改前后指针,形成双向循环链表
for (int i = 0; i < n; ++i) {
// 前驱节点:i-1,第一个节点的前驱是最后一个节点
nodes[i]->left = nodes[(i - 1 + n) % n];
// 后继节点:i+1,最后一个节点的后继是第一个节点
nodes[i]->right = nodes[(i + 1) % n];
}
// 返回链表中最小元素的指针(即vector的第一个节点)
return nodes[0];
}
private:
// 中序遍历辅助函数
void inorderTraversal(Node* root, vector<Node*>& nodes) {
if (root == nullptr) {
return;
}
inorderTraversal(root->left, nodes);
nodes.push_back(root);
inorderTraversal(root->right, nodes);
}
};
cpp
//思路二
class Solution {
public:
void InOrderConvert(Node* cur, Node*& prev)
{
if(cur == nullptr)
return;
InOrderConvert(cur->left, prev);
// cur中序
// left指向中序前一个,左变成前驱
cur->left = prev;
// 中序前一个节点的右指向cur,右变成后继
if(prev)
prev->right = cur;
prev = cur;
InOrderConvert(cur->right, prev);
}
Node* treeToDoublyList(Node* root) {
if(root == nullptr) {
return nullptr;
}
Node* prev = nullptr;
InOrderConvert(root, prev);
Node* head = root;
while(head->left)
{
head = head->left;
}
// 循环链表
head->left = prev;
prev->right = head;
return head;
}
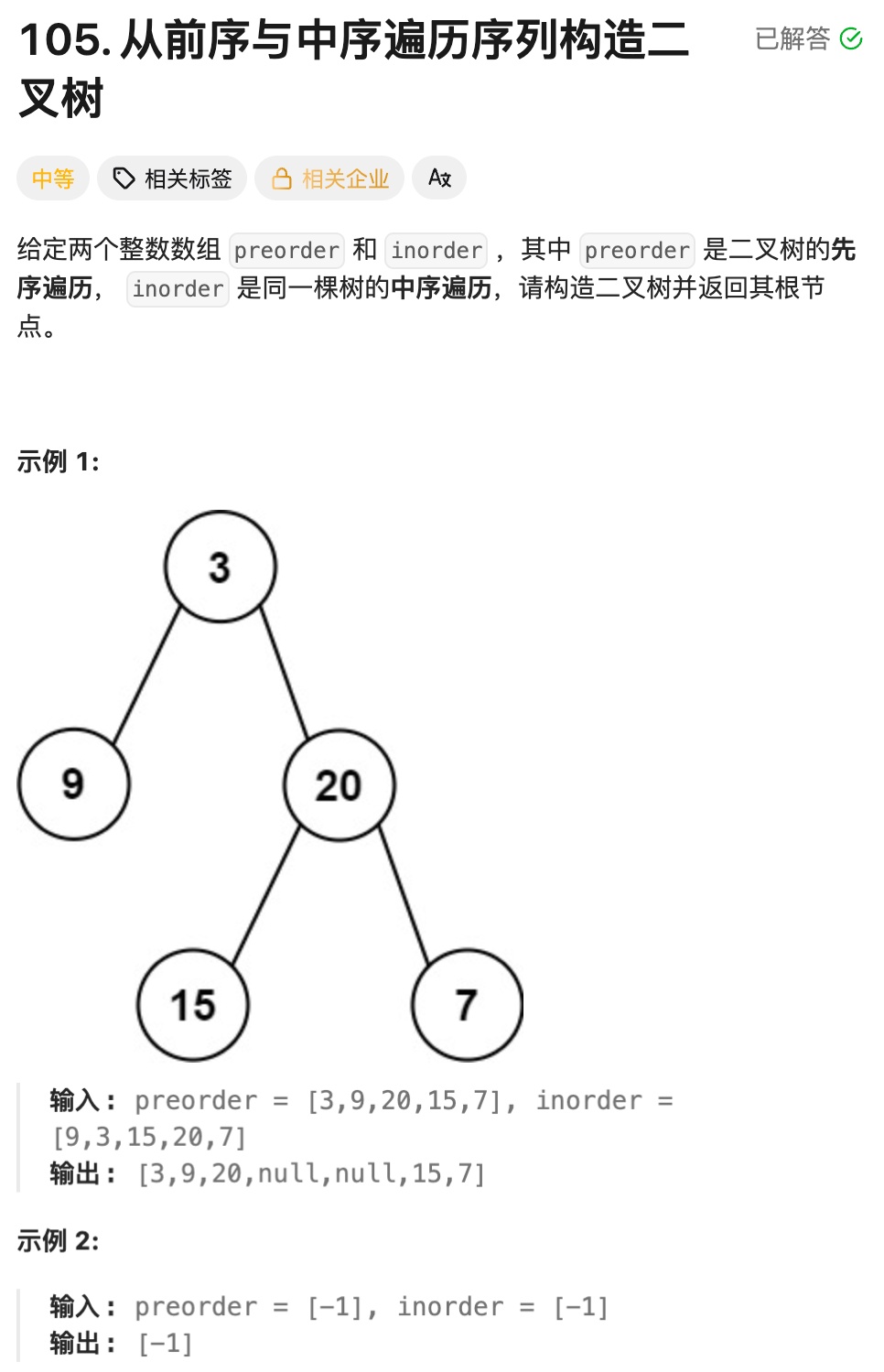
};8.6从前序与中序遍历序列构造⼆叉树
实现思路:
①主函数:初始化与递归入口
buildTree 是对外的核心接口,负责初始化递归所需的参数:定义前序遍历的索引变量 i 并初始化为0(i 指向当前待处理的根节点,初始指向整棵树的根);
调用辅助函数build,传入前序数组、中序数组、i 的引用(保证递归中索引全局递增)、中序序列的初始范围(inbegin=0,inend=inorder.size()-1);返回辅助函数构建的整棵树的根节点.
②辅助函数build:递归构建子树
递归终止条件:当中序序列的起始索引 inbegin > 结束索引 inend 时,说明当前子树无节点(空树),直接返回nullptr.
确定当前子树的根节点:前序数组中 preorder[prei] 是当前子树的根节点(前序遍历 "根优先" 的特性),据此创建 TreeNode 对象作为当前子树的根;
在中序序列中定位根节点,分割左右子树:遍历中序序列的 [inbegin, inend] 范围,找到值等于 preorder[prei] 的索引rooti;
分割逻辑:[inbegin, rooti-1]:当前根节点左子树的中序序列;rooti:当前根节点在中序序列中的位置;rooti+1, inend\]:当前根节点右子树的中序序列. 更新前序索引,递归构建左右子树:将prei 自增1指向下一个待处理的根节点,即左子树的根); 递归构建左子树:调用build,传入左子树的中序范围 \[inbegin, rooti-1\],返回值赋值给 root-\>left; 递归构建右子树:调用build,传入右子树的中序范围 \[rooti+1, inend\],返回值赋值给 root-\>right. 返回当前子树的根节点:递归逐层返回构建好的子树根节点,最终向上拼接成完整的二叉树. 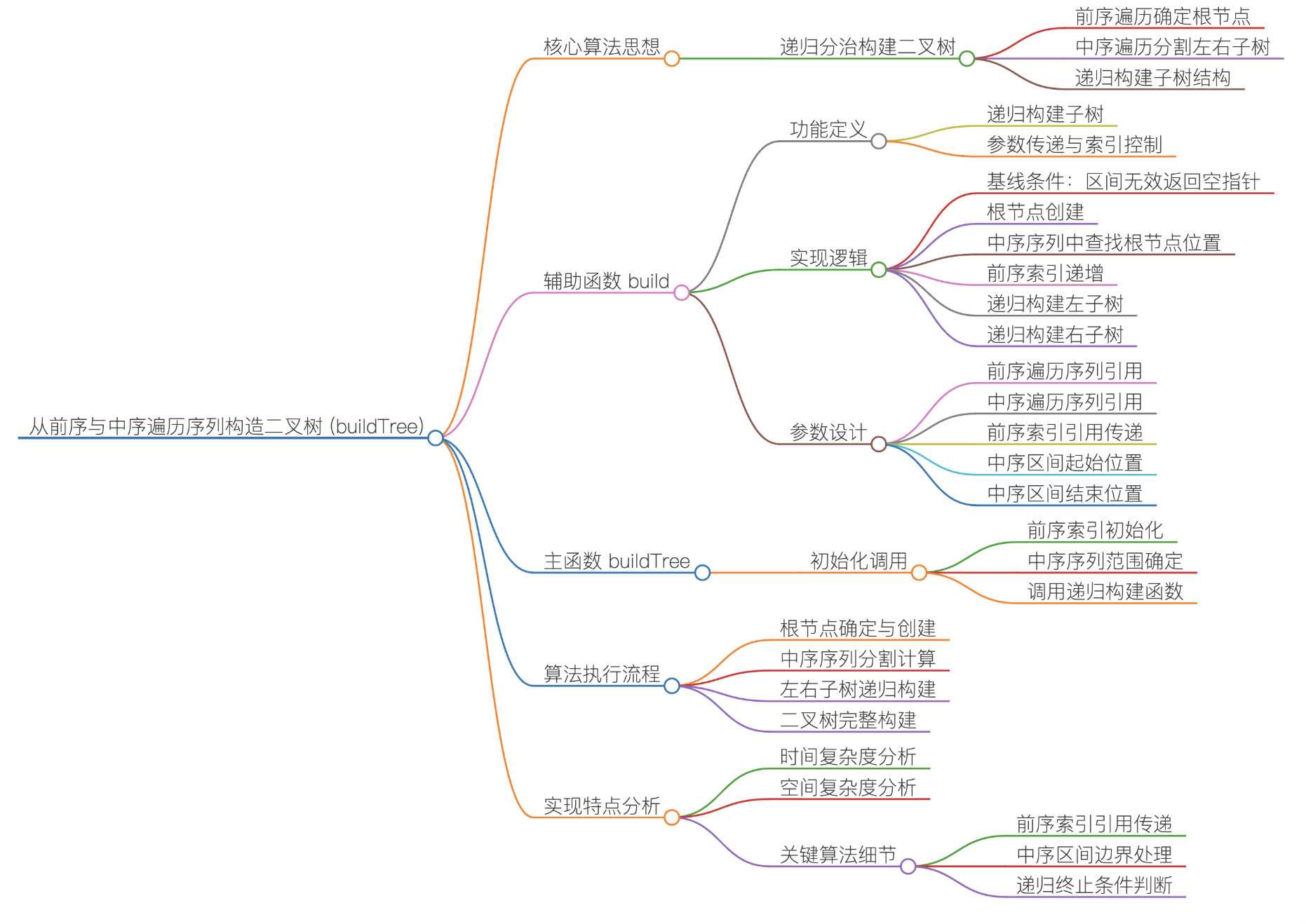
cpp
class Solution {
public:
TreeNode* build(vector<int>& preorder, vector<int>& inorder, int& prei, int inbegin, int inend)
{
if(inbegin > inend)
return nullptr;
// 前序确定根
TreeNode* root = new TreeNode(preorder[prei]);
// 中序分割左右子树
int rooti = inbegin;
while(rooti <= inend)
{
if(preorder[prei] == inorder[rooti])
break;
else
rooti++;
}
prei++;
// [inbegin, rooti-1] rooti [rooti+1, inend];
root->left = build(preorder, inorder, prei, inbegin, rooti-1);
root->right = build(preorder, inorder, prei, rooti+1, inend);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int i = 0;
return build(preorder, inorder, i, 0, inorder.size()-1);
}
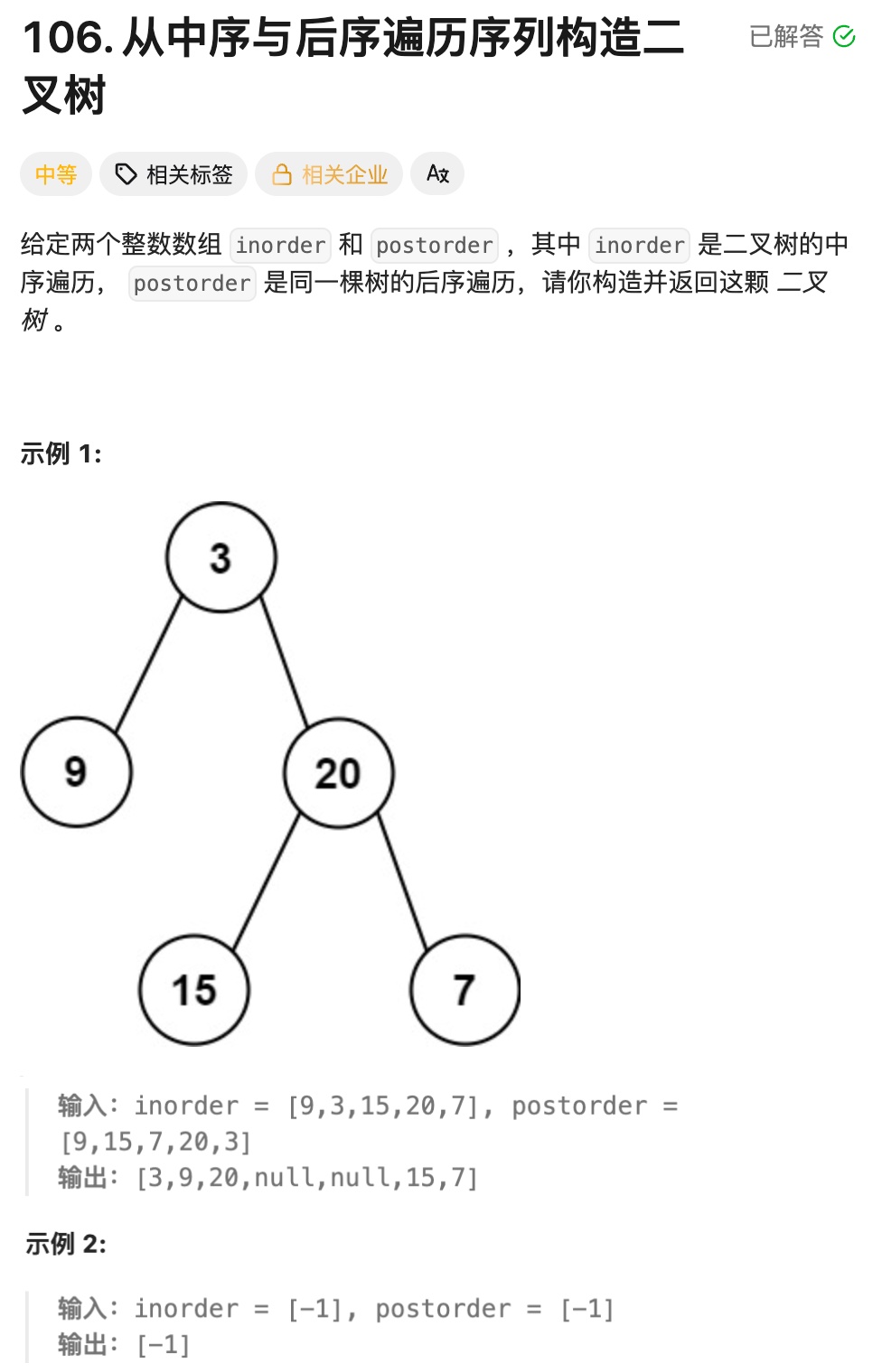
};8.7从中序与后序遍历序列构造⼆叉树
实现思路:
①主函数:初始化与递归入口
buildTree 是对外接口,负责初始化递归核心参数:
定义后序遍历的索引变量 posti 并初始化为 postorder.size() - 1(后序最后一个元素是整棵树的根节点);调用辅助函数build,传入中序数组、后序数组、posti 的引用(保证递归中索引全局递减)、中序序列的初始范围(inbegin=0,inend=inorder.size()-1);返回辅助函数构建的整棵树的根节点.
②辅助函数build:递归构建子树
递归终止条件:当中序序列的起始索引 inbegin > 结束索引 inend 时,说明当前子树无节点(空树),直接返回nullptr.
确定当前子树的根节点:后序数组中 postorder[posti] 是当前子树的根节点(后序遍历 "根最后" 的特性),据此创建 TreeNode 对象作为当前子树的根.
在中序序列中定位根节点,分割左右子树:遍历中序序列的 [inbegin, inend] 范围,找到值等于 postorder[posti] 的索引rooti;
分割逻辑:[inbegin, rooti-1]:当前根节点左子树的中序序列;
rooti:当前根节点在中序序列中的位置;rooti+1, inend\]:当前根节点右子树的中序序列. 更新后序索引,递归构建左右子树:将 posti 自减1(指向前一个待处理的根节点,后序从后往前取,下一个是右子树的根); 先递归构建右子树:调用 build,传入右子树的中序范围 \[rooti+1, inend\],返回值赋值给 root-\>right; 再递归构建左子树:调用 build,传入左子树的中序范围 \[inbegin, rooti-1\],返回值赋值给 root-\>left; ✅ 关键原因:后序遍历顺序是 "左→右→根",从后往前取元素时,先取到的是 "右子树的根",再取到 "左子树的根".因此必须先构建右子树,再构建左子树. 返回当前子树的根节点:递归逐层返回构建好的子树根节点,最终向上拼接成完整的二叉树. 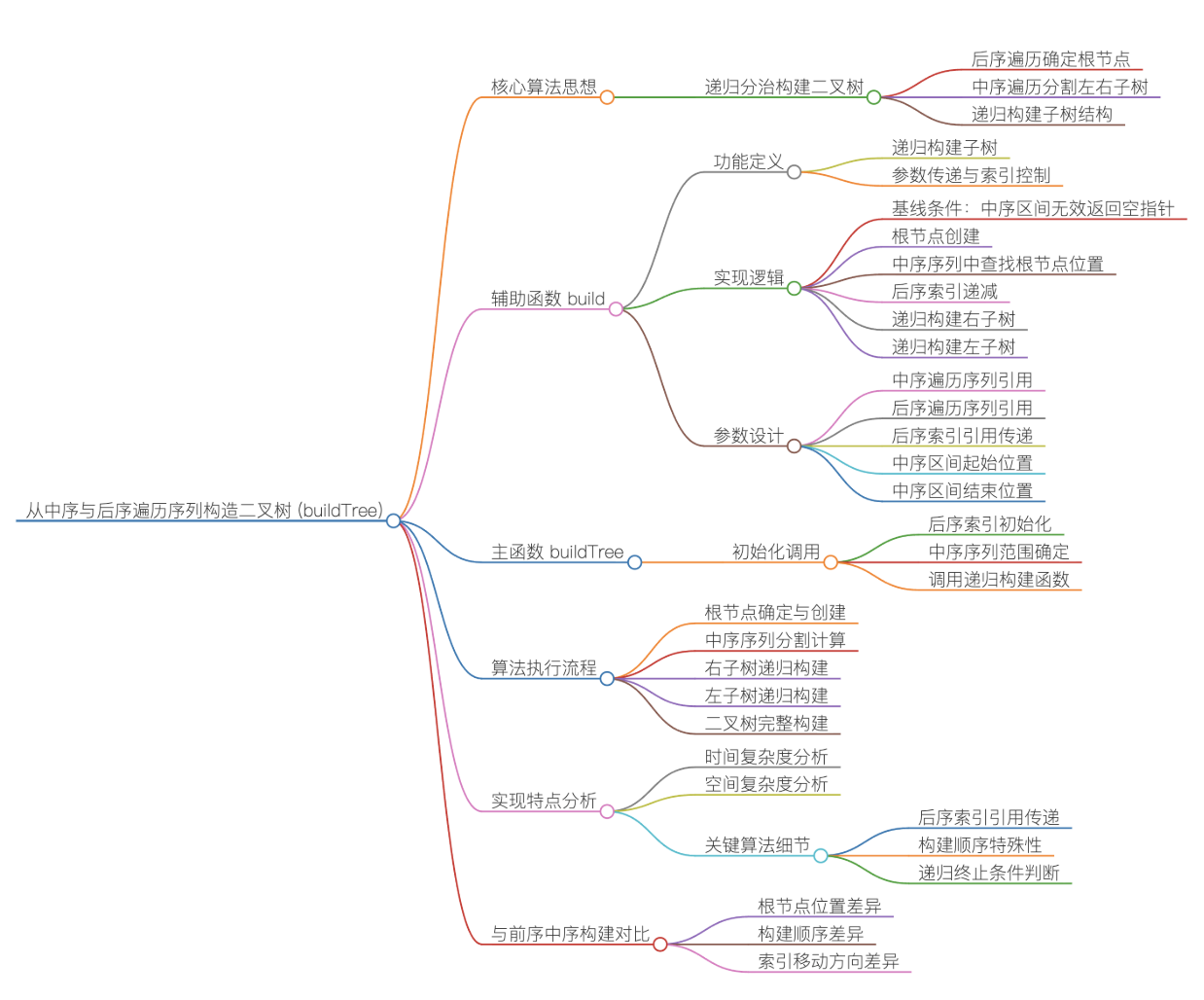
cpp
class Solution {
public:
TreeNode* build(vector<int>& inorder, vector<int>& postorder, int& posti, int inbegin, int inend) {
// 递归终止条件:中序区间为空,返回空节点
if (inbegin > inend) {
return nullptr;
}
// 后序遍历的最后一个元素是当前子树的根节点
TreeNode* root = new TreeNode(postorder[posti]);
// 在中序遍历中找到根节点的位置,用于分割左右子树
int rooti = inbegin;
while (rooti <= inend) {
if (inorder[rooti] == postorder[posti]) {
break;
}
rooti++;
}
// 后序索引向前移动一位,下一个根节点是右子树的根(后序顺序:左→右→根)
posti--;
// 注意:必须先构建右子树,再构建左子树
// 因为后序数组从后往前取,先取到右子树的根,再取到左子树的根
root->right = build(inorder, postorder, posti, rooti + 1, inend);
root->left = build(inorder, postorder, posti, inbegin, rooti - 1);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
// 后序索引初始化为最后一个元素(整棵树的根节点)
int posti = postorder.size() - 1;
return build(inorder, postorder, posti, 0, inorder.size() - 1);
}
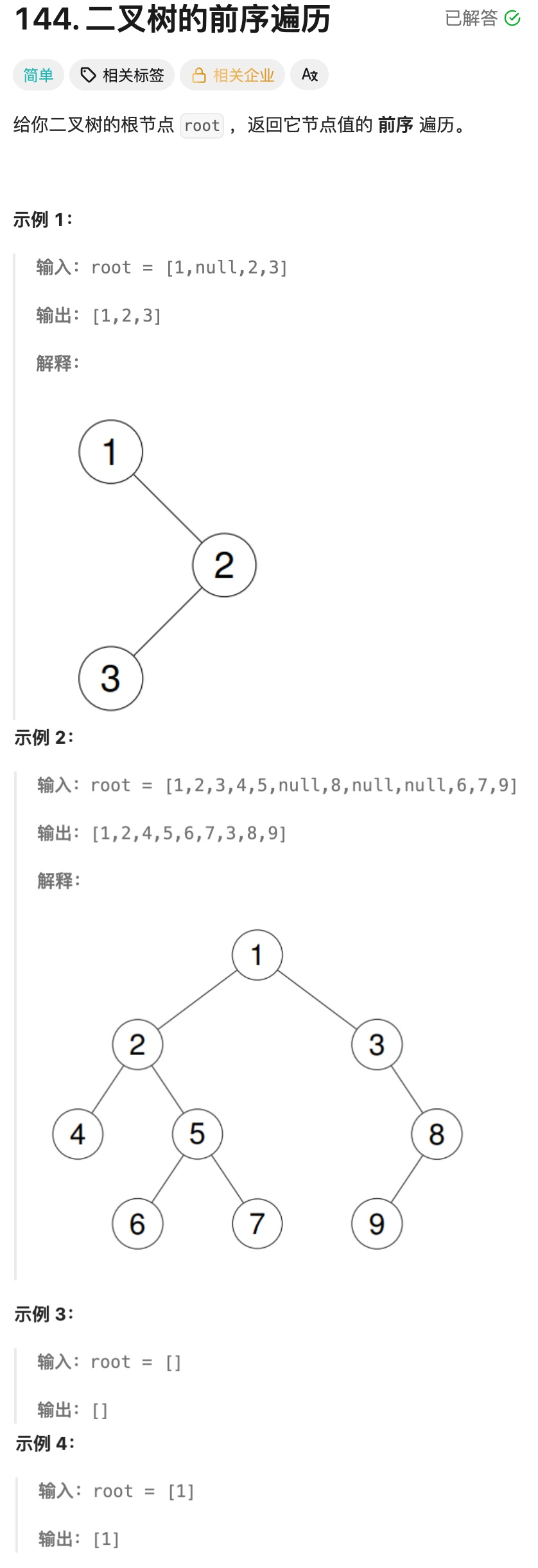
};8.8二叉树前序遍历
⾮递归迭代实现思想:
要迭代⾮递归实现⼆叉树前序遍历,⾸先还是要借助递归的类似的思想,只是需要把结点存在栈中,⽅便类似递归回退时取⽗路径结点.跟这⾥不同的是,这⾥把⼀棵⼆叉树分为两个部分:
①先访问左路结点
②再访问左路结点的右⼦树
这⾥访问右⼦树要以循环从栈依次取出这些结点,循环⼦问题的思想访问左路结点的右⼦树.中序和后序跟前序的思路完全⼀致,只是前序先访问根还是后访问根的问题.后序稍微⿇烦⼀些,因为后序遍历的顺序是左⼦树、右⼦树、根,当取到左路结点的右⼦树时,需要想办法标记判断右⼦树是否访问过了,如果访问过了,就直接访问根,如果访问过需要先访问右⼦树.
cpp
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> s;
vector<int> v;
TreeNode* cur = root;
while(cur || !s.empty())
{
// 访问⼀颗树的开始
// 1、访问左路结点,左路结点⼊栈
while(cur)
{
v.push_back(cur->val);
s.push(cur);
cur = cur->left;
}
// 2、从栈中依次访问左路结点的右⼦树
TreeNode* top = s.top();
s.pop();
// 循环⼦问题⽅式访问左路结点的右⼦树 --
cur = top->right;
}
return v;
}
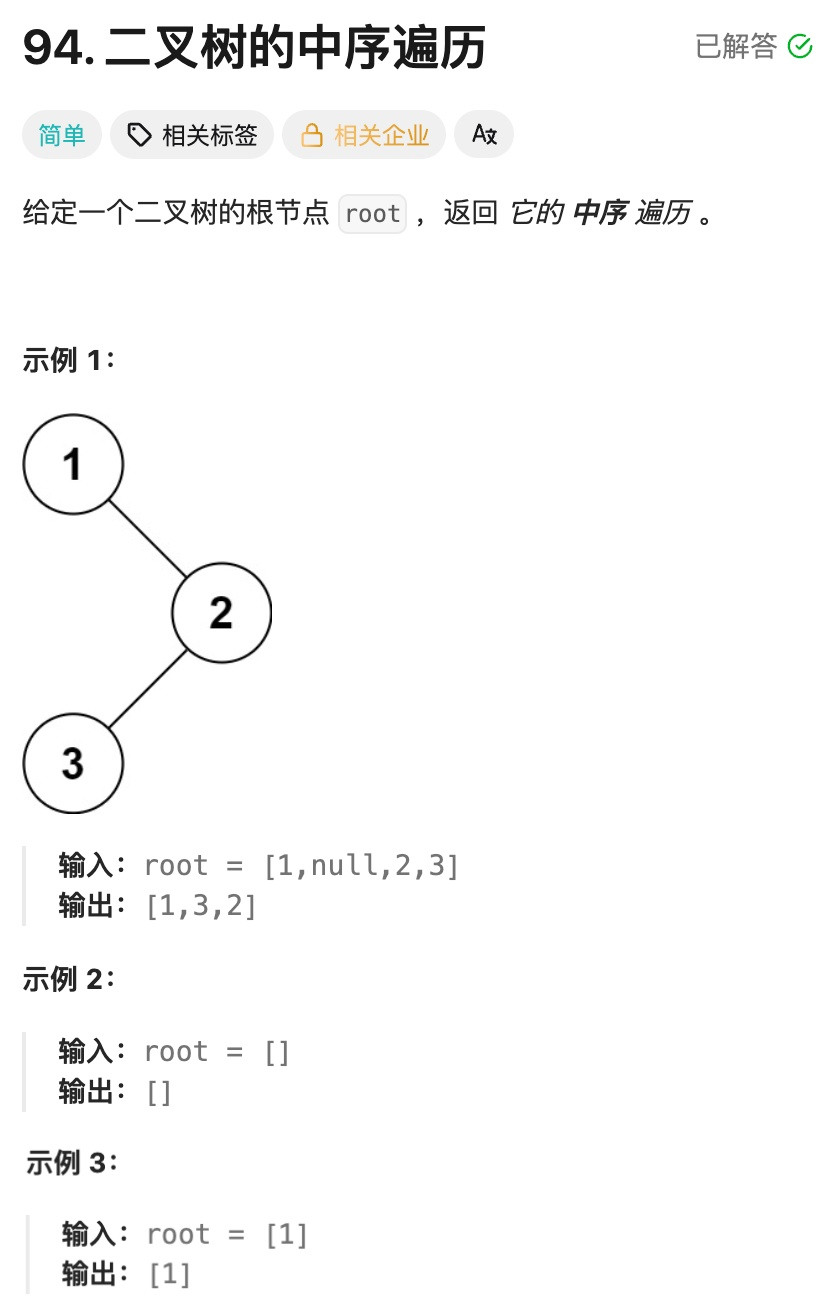
};8.9二叉树的中序遍历
cpp
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
TreeNode* cur = root;
vector<int> v;
while(cur || !st.empty())
{
// 访问⼀颗树的开始
// 1、左路结点⼊栈
while(cur)
{
st.push(cur);
cur = cur->left;
}
// 访问问左路结点 和 左路结点的右⼦树
TreeNode* top = st.top();
st.pop();
v.push_back(top->val);
// 循环⼦问题⽅式访问右⼦树
cur = top->right;
}
return v;
}
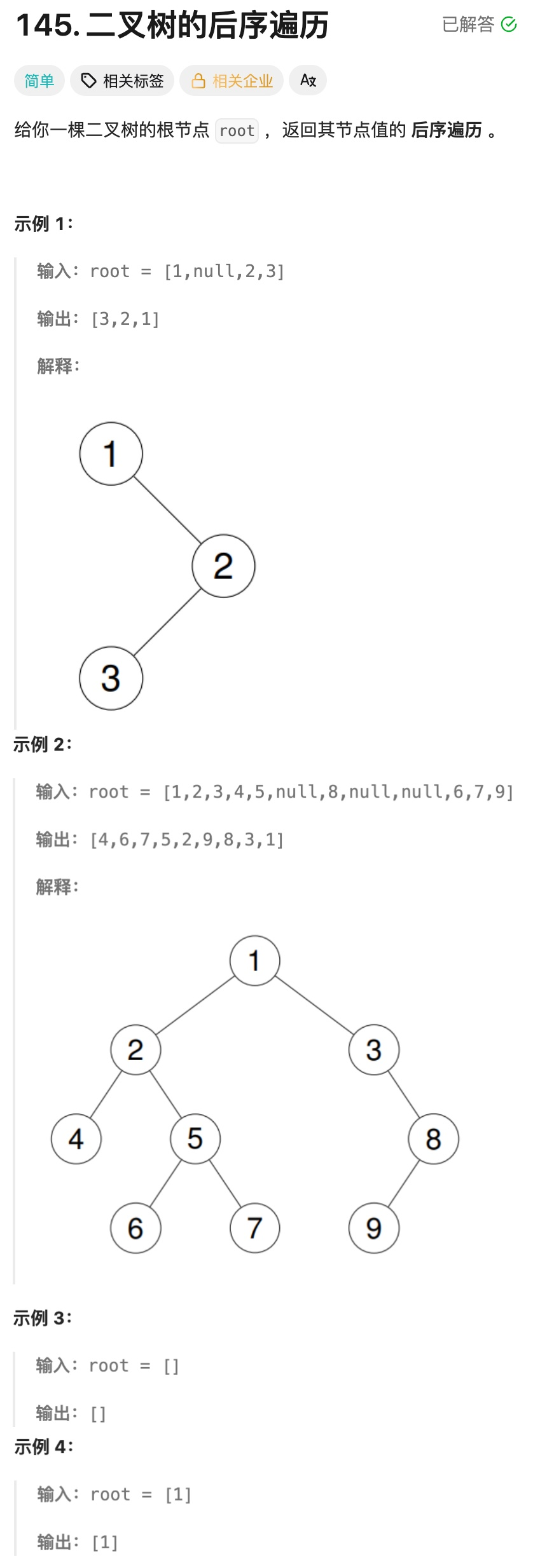
};8.10二叉树的后序遍历
cpp
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
TreeNode* cur = root;
stack<TreeNode*> s;
vector<int> v;
TreeNode* prev = nullptr;
while(cur || !s.empty())
{
// 1、访问⼀颗树的开始
while(cur)
{
s.push(cur);
cur = cur->left;
}
TreeNode* top = s.top();
// top结点的右为空 或者 上⼀个访问结点等于他的右孩⼦
// 那么说明(空)不⽤访问 或者 (不为空)右⼦树已经访问过了
// 那么说明当前结点左右⼦树都访问过了,可以访问当前结点了
if(top->right == nullptr || top->right == prev)
{
s.pop();
v.push_back(top->val);
prev = top;
}
else
{
// 右⼦树不为空,且没有访问,循环⼦问题⽅式右⼦树
cur = top->right;
}
}
return v;
}
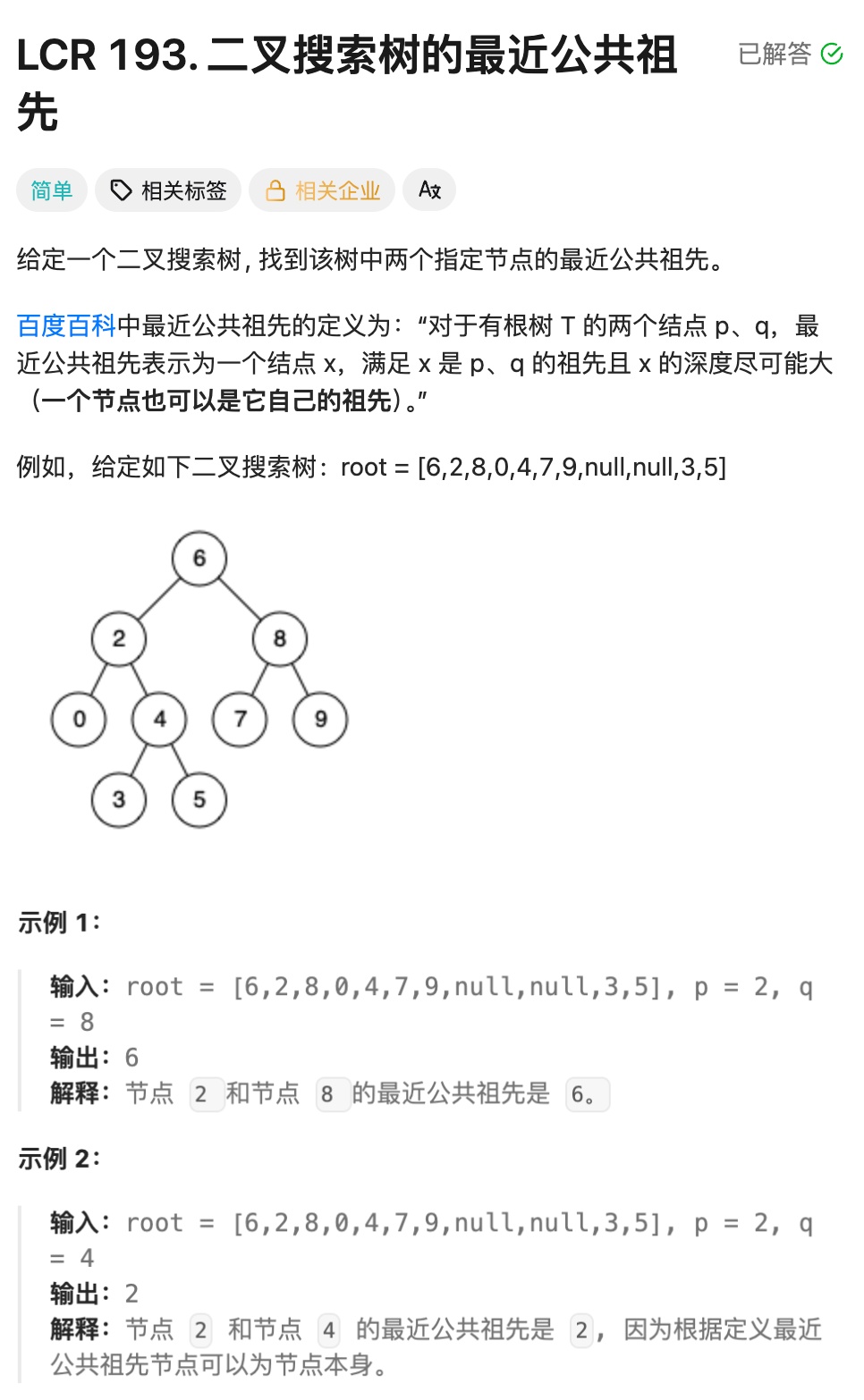
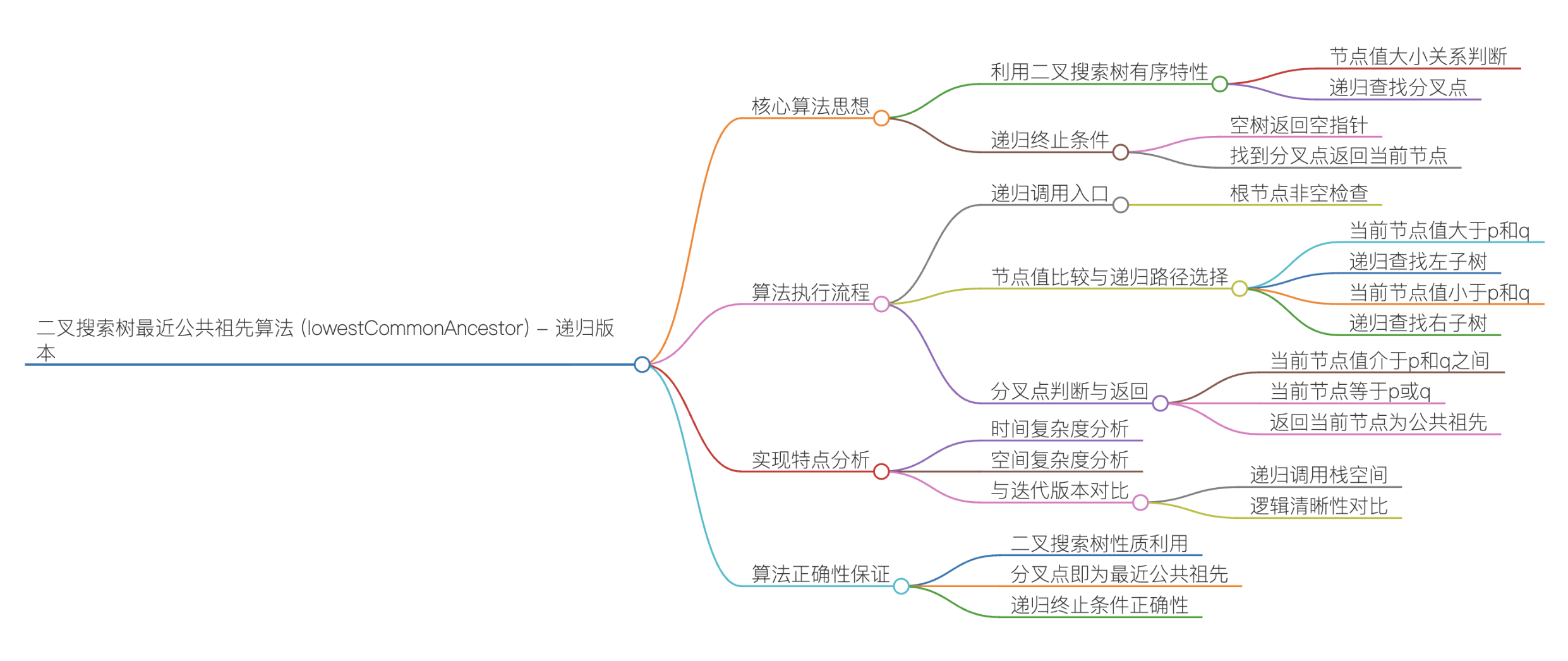
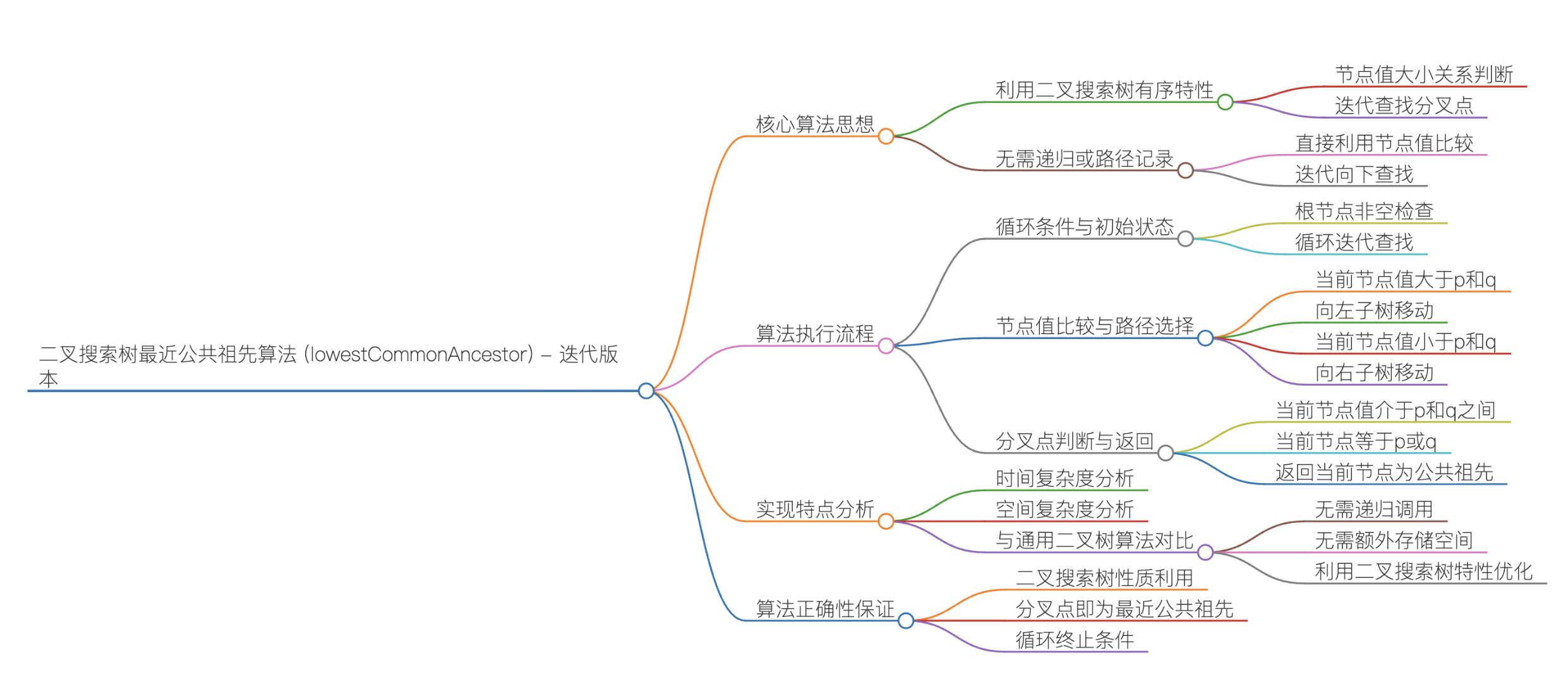
};8.11二叉搜索树的最近公共祖先
cpp
//递归思路
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
// 递归终止条件:空树或找到分叉点
if (root == nullptr) return nullptr;
// 当前节点值 > p和q的值 → p、q都在左子树
if (root->val > p->val && root->val > q->val) {
return lowestCommonAncestor(root->left, p, q);
}
// 当前节点值 < p和q的值 → p、q都在右子树
else if (root->val < p->val && root->val < q->val) {
return lowestCommonAncestor(root->right, p, q);
}
// 否则,当前节点就是最近公共祖先(p、q分属左右子树,或其中一个就是当前节点)
else {
return root;
}
}
};
cpp
//迭代思路
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
while (root != nullptr) {
// 当前节点值 > p和q的值 → 向左子树查找
if (root->val > p->val && root->val > q->val) {
root = root->left;
}
// 当前节点值 < p和q的值 → 向右子树查找
else if (root->val < p->val && root->val < q->val) {
root = root->right;
}
// 找到分叉点,返回当前节点
else {
return root;
}
}
return nullptr; // 题目保证p、q存在,此分支不会触发
}
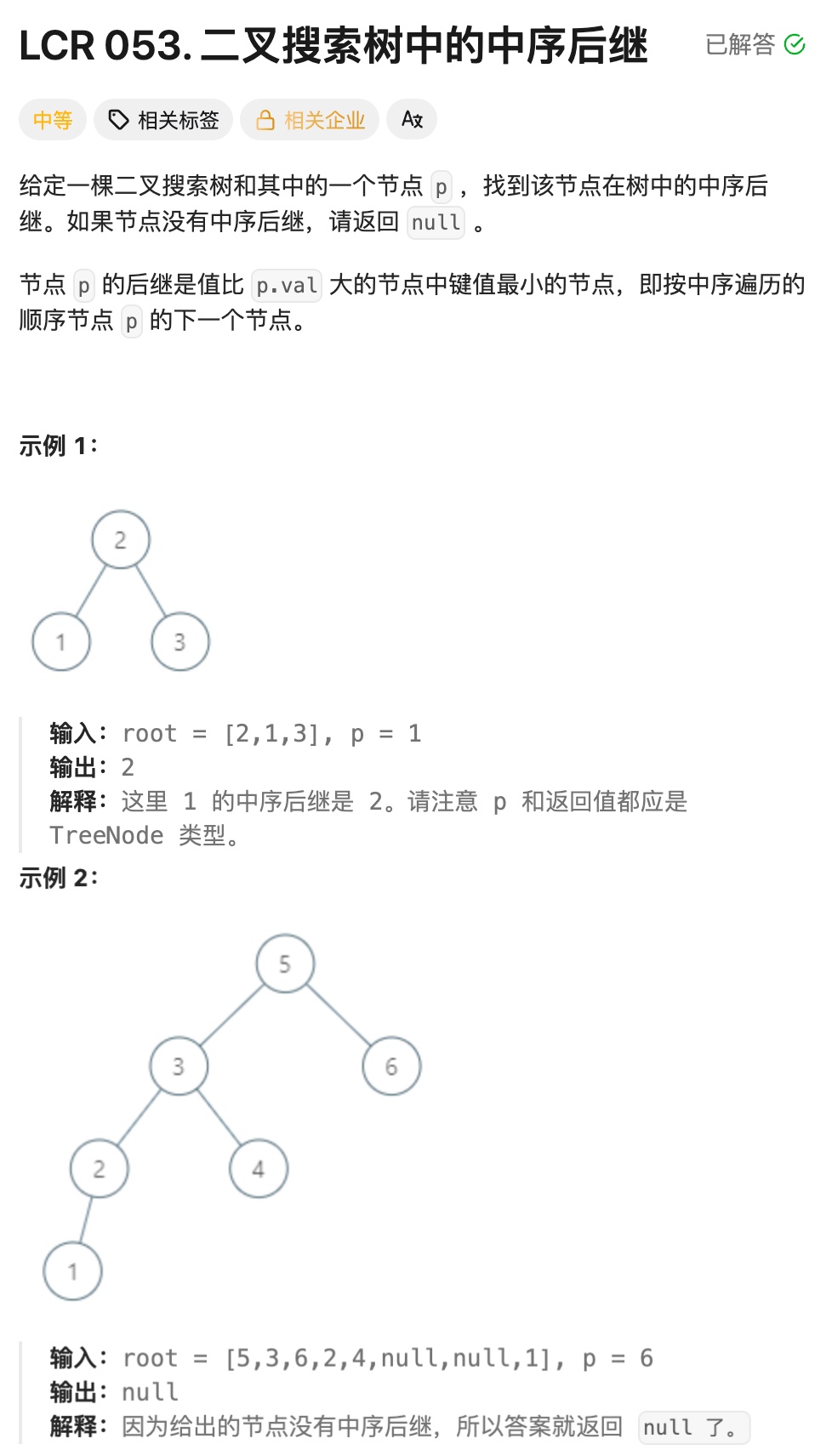
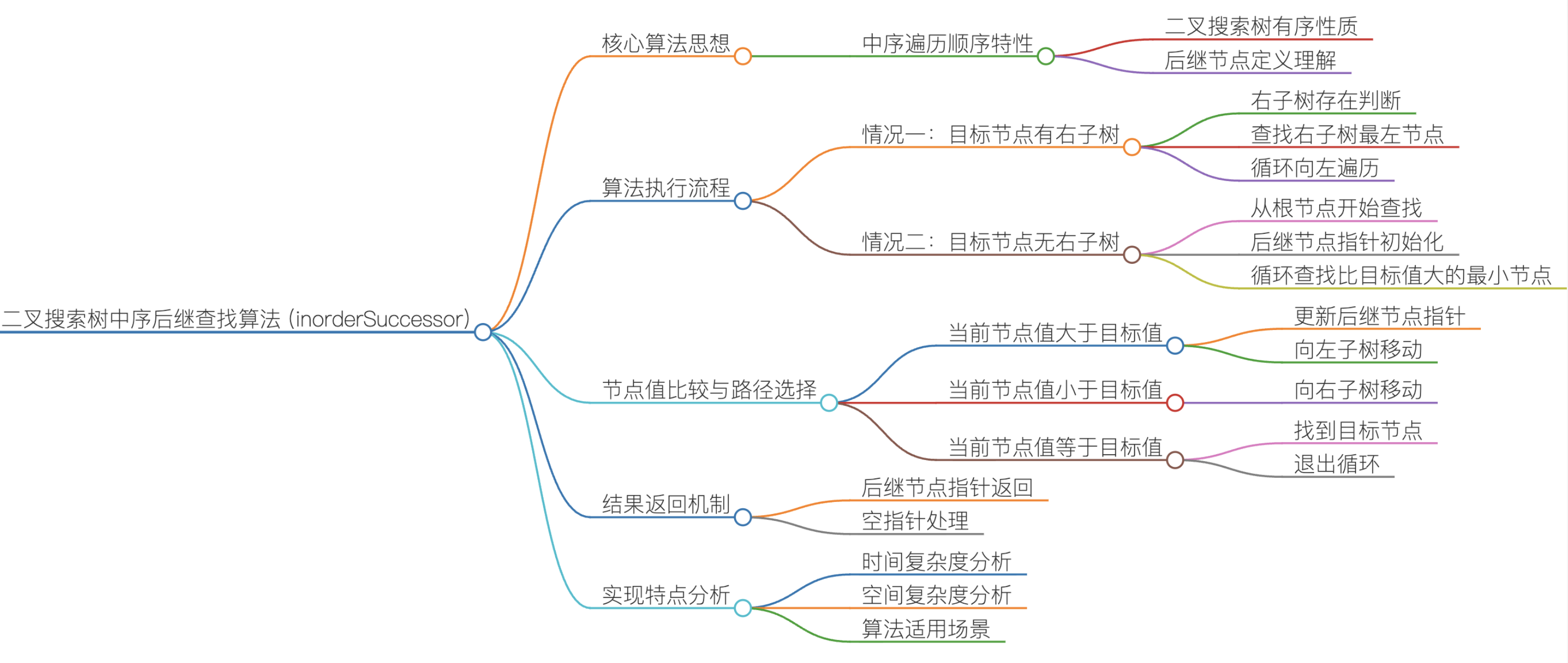
};8.12二叉搜索树中的中序后继
实现思路:
p 有右子树(最直接的情况)
核心原理:中序遍历顺序是左 → 根 → 右,p 的右子树中最左侧的节点是右子树里值最小的节点,也就是整个树中比 p 大的最小节点(即 p 的中序后继).
执行步骤:
若 p->right != nullptr,定义临时变量 cur 指向 p->right;
让 cur 不断向左遍历(cur = cur->left),直到 cur->left == nullptr(找到右子树的最左节点);直接返回这个最左节点,即为 p 的中序后继.
p没有右子树(需要回溯找祖先)
核心原理:p 没有右子树时,其中序后继是 "从根节点到 p 的路径中,最近的、值比 p 大的祖先节点";若没有这样的祖先,说明 p 是中序遍历的最后一个节点,后继为nullptr.
执行步骤:
初始化两个变量:successor(记录候选后继,初始为nullptr)、cur(遍历指针,初始指向根节点);
循环遍历树(cur != nullptr):
若cur->val > p->val:说明 cur 是候选后继(比 p 大),先将successor = cur,再向左子树遍历(尝试找更小的、更接近 p 的后继);
若cur->val < p->val:说明后继在右子树,让cur向右遍历(cur = cur->right);
若cur->val == p->val:找到 p 节点,退出循环(无需继续遍历);
循环结束后,successor 中存储的就是 p 的中序后继(若存在),直接返回.
cpp
class Solution {
public:
TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
// 情况1:p有右子树,后继是右子树的最左节点
if (p->right != nullptr) {
TreeNode* cur = p->right;
while (cur->left != nullptr) {
cur = cur->left;
}
return cur;
}
// 情况2:p没有右子树,从根开始找比p大的最小节点
TreeNode* successor = nullptr;
TreeNode* cur = root;
while (cur != nullptr) {
if (cur->val > p->val) {
successor = cur;
cur = cur->left;
} else if (cur->val < p->val) {
cur = cur->right;
} else {
break; // 找到p节点,退出循环
}
}
return successor;
}
};8.13验证二叉搜索树的后序遍历序列
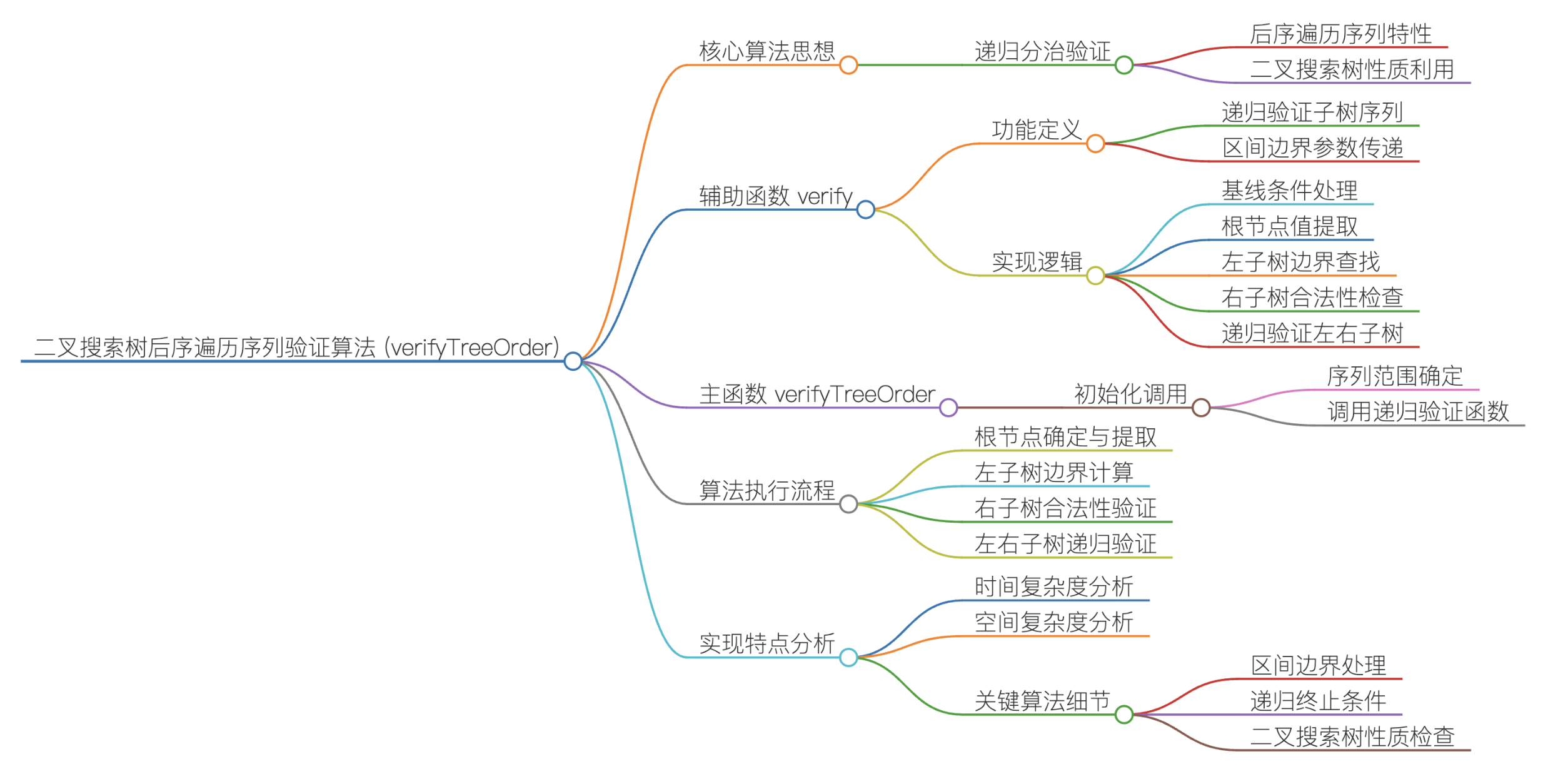
实现思路:
①主函数:入口封装
verifyTreeOrder是对外的核心接口,仅做简单封装:调用私有辅助函数 verify,传入整个序列的遍历范围(start=0,end=postorder.size()-1),并返回验证结果.
②辅助函数 verify:递归分治验证
递归终止条件:当 start >= end时(空区间或只有一个节点),说明当前子树无节点或仅有一个节点,天然符合 BST 后序序列规则,直接返回 true.
确定当前子树的根节点:后序遍历的最后一个元素(postorder[end])是当前子树的根节点,记为 rootVal(后序 "根在最后" 的特性).
划分左子树范围:从 start 开始遍历序列,找到第一个大于 rootVal 的位置i:区间 [start, i-1] 是当前根节点的左子树(BST 左子树所有节点值 < 根节点);
遍历终止条件:i < end 且 postorder[i] < rootVal,超出范围或遇到大于根节点的值时停止.
验证右子树合法性:从分界点 i 开始遍历到 end-1(排除根节点),检查该区间内所有节点值是否都大于rootVal:若存在任意节点值 < rootVal,说明违反 BST"右子树所有节点> 根节点" 的规则,直接返回 false;
若全部符合,说明当前根节点的右子树区间 [i, end-1] 初步合法.
递归验证左右子树:分别递归验证左子树([start, i-1])和右子树([i, end-1])的合法性:
只有左右子树都验证通过(返回 true),当前子树才合法;
最终返回左右子树验证结果的 "与" 运算(&&).
③最终结果
递归逐层验证后,返回整个序列是否符合 BST 后序遍历规则的布尔值.
cpp
class Solution {
public:
bool verifyTreeOrder(vector<int>& postorder) {
return verify(postorder, 0, postorder.size() - 1);
}
private:
bool verify(vector<int>& postorder, int start, int end) {
// 空区间或单个节点
if (start >= end) {
return true;
}
// 后序遍历最后一个节点是根节点
int rootVal = postorder[end];
int i = start;
// 找到左子树的边界:所有小于根节点的节点
while (i < end && postorder[i] < rootVal) {
i++;
}
// 检查右子树所有节点是否都大于根节点
int j = i;
while (j < end) {
if (postorder[j] < rootVal) {
return false;
}
j++;
}
// 递归验证左子树 [start, i-1] 和右子树 [i, end-1]
return verify(postorder, start, i - 1) && verify(postorder, i, end - 1);
}
};敬请期待下一篇文章内容-->C++map和set的使⽤相关内容!
每日心灵鸡汤:
努力不是为了证明自己有多优秀,而是为了在意外来临时,那些平常所努力积淀的涵养和能力,可以成为抗衡一切风雨的底气."人习于苟且非一日,士大夫多以不恤国事、同俗自媚于众为善!"
生活不会亏待那些愿意努力的人.你现在所吃的苦、受的累、掉的坑,到最后都会变成黑夜里那道耀眼的光,照亮你前进的路,成就未来更好的自己!